Основы логики (алгебра логики)

Основы логики

Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Истинность – 1, ложь - 0

Так, например, предложение

" Трава зеленая " следует считать высказыванием, так как оно истинное.

Предложение " Лев - птица " тоже высказывание, так как оно ложное.

Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если... , то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания.

Такие слова и словосочетания называются логическими связками .

• Bысказывания, образованные из других высказываний с помощью логических связок, называются составными.
• Высказывания, не являющиеся составными, называются элементарными .
• Так, например, из элементарных высказываний " Петров — врач ", " Петров — шахматист " при помощи связки " и " можно получить составное высказывание " Петров — врач и шахматист ", понимаемое как " Петров — врач, хорошо играющий в шахматы ".

Операции над логическими

высказываниями

• Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний

Логическое отрицание (инверсия)

Обозначение инверсии: НЕ А; А; A; NOT A

Логическое отрицание образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что …».

А

 А

0

1

1

0

Логическое умножение (конъюнкция)

Обозначение конъюнкции: А И В; А  В; А&B; A AND B.

Логическое умножение образуется соединением двух высказываний в одно с помощью союза «и».

Из таблицы истинности следует, что конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.

А

В

0

0

А&B

0

1

0

1

0

0

1

1

0

1

Логическое сложение (дизъюнкция)

Обозначение конъюнкции: А ИЛИ В; А  В; А  B; A OR B; А+В.

Логическое сложение образуется соединением двух высказываний в одно с помощью союза «или».

А

В

0

0

0

А  В

1

0

1

1

0

1

1

1

1

Из таблицы истинности следует, что дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.

Логическое следование (импликация)

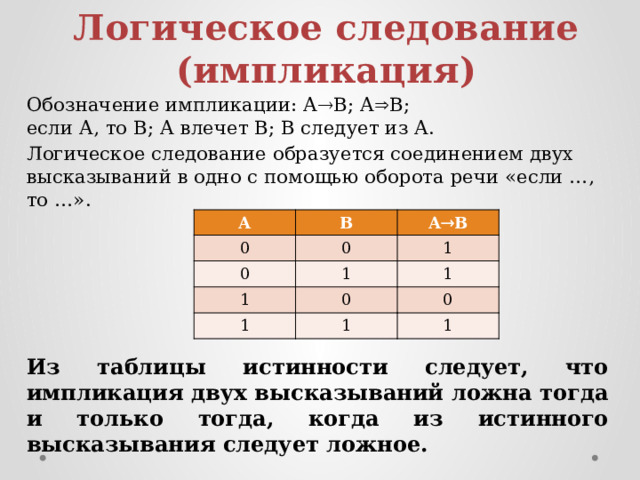
Обозначение импликации: А  В; А  B; если А, то В; А влечет В; В следует из А.

Логическое следование образуется соединением двух высказываний в одно с помощью оборота речи «если …, то …».

А

0

В

0

0

А  В

1

1

1

1

1

0

0

1

1

Из таблицы истинности следует, что импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное.

Логическое равенство (эквивалентность)

Обозначение эквивалентности: А  В; А  B; А  В.

Логическое равенство образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда …».

А

0

В

0

0

А  B

1

1

1

1

0

0

0

1

1

Из таблицы истинности следует, что эквивалентность двух высказываний ложна тогда и только тогда, когда оба высказывания истинны или оба ложны.

Порядок выполнения логических операций в сложном логическом выражении :

1. инверсия

2. конъюнкция

3. дизъюнкция

4. импликация

5. эквивалентность

Для изменения указанного порядка  

выполнения операций используются скобки.