Основы логики. Логические выражения и таблицы истинности.

ПРЕЗЕНТАЦИЯ тема:

1.Логические выражения и таблицы истинности.

2.Логические законы и правила преобразования выражений.

3.Решение логических задач.

1. Логические выражения и таблицы истинности. 1.1. Логические выражения.

Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные , обозначающие высказывания, и знаки логических операций , обозначающие логические функции.

Для этого в составном высказывании нужно выделить простые высказывания и логические связи между ними.

Для примера возьмем следующее логическое высказывание:

(2 * 2 = 5 или 2 * 2 = 4) и (2 * 2 ≠ 5 или 2 * 2 ≠ 4 )

Проанализируем составное высказывание:

А = (2 * 2 = 5) ложно (0)

В = (2 * 2 = 4) истинно (1)

Тогда можно записать:

(А или В) и (¬А или ¬В)

Теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполняемых логических операций:

F = (A \/ B ) & (¬A \/ ¬B)

Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:

F = (A \/ B ) & (¬A \/ ¬B) = (0 \/ 1 ) & (1 \/ 0) = 1 & 1 = 1

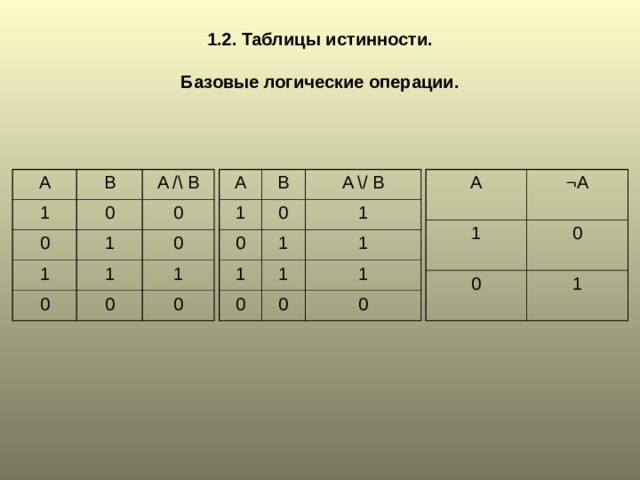
1.2. Таблицы истинности. Базовые логические операции.

A

A

1

¬A

A

B

0

B

0

1

1

0

0

A \/ B

1

A /\ B

0

0

1

1

0

1

1

1

0

1

1

0

1

0

0

0

1

1

0

0

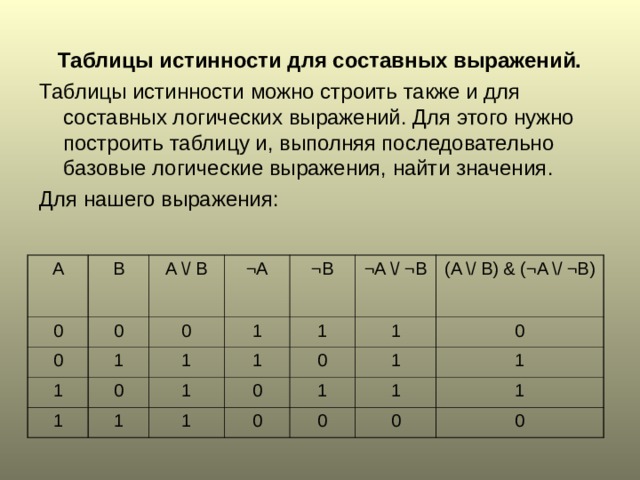
Таблицы истинности для составных выражений.

Таблицы истинности можно строить также и для составных логических выражений. Для этого нужно построить таблицу и, выполняя последовательно базовые логические выражения, найти значения .

Для нашего выражения:

A

0

B

0

A \/ B

0

¬A

0

1

1

¬B

1

1

0

1

1

¬A \/ ¬B

1

1

1

0

1

(A \/ B) & (¬A \/ ¬B)

0

1

0

0

1

1

0

1

1

1

0

0

2.Логические законы и правила преобразования выражений.

Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Важное значение для выполнения преобразований логических выражений имеют законы алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.

Закон тождества. Всякое высказывание тождественно самому себе:

А = А

Закон непротиворечия.

А & ¬А = 0

Закон исключенного третьего.

А \/ ¬ А = 1

Закон двойного отрицания.

¬(¬А) = А

Законы де Моргана.

¬(А \/ В) = ¬А & ¬В

¬(А & В) = ¬А \/ ¬В

___________________________________________________

Закон коммутативности:

Закон ассоциативности:

Закон дистрибутивности:

Логическое умножение

A & B = B & A

Логическое сложение

A \/ B = B \/ A

Логическое умножение

( A & B ) & C = A & (B & C)

Логическое сложение

( A \/ B ) \/ C = A \/ (B \/ C)

Логическое умножение

Логическое сложение

(A & B) \/ (A & C) = A & (B \/ C)

(A \/ B) & (A \/ C) = A \/ (B & C)

3. Решение логических задач.

Логические задачи обычно формулируются на естественном языке. В первую очередь их необходимо формализовать, т. е. записать на языке алгебры высказываний. Полученные логические выражения необходимо упростить и проанализировать. Для этого иногда бывает необходимо построить таблицу истинности полученного логического выражения.

Условие задачи

В школе-новостройке в каждой из двух аудиторий может находиться либо кабинет информатики, либо кабинет физики. На дверях аудиторий повесили шутливые таблички. На первой повесили табличку: «По крайней мере, в одной из этих аудиторий размещается кабинет информатики», а на второй аудитории – табличку с надписью «Кабинет физики находиться в другой аудитории». Проверяющему, который пришел в школу, известно только, что надписи на табличках либо обе истинны, либо обе ложны. Помогите проверяющему найти кабинет информатики.

Переведем условие на язык логических высказываний. Пусть:

А = «В первой аудитории размещается кабинет информатики»

В = «Во второй аудитории размещается кабинет информатики»

Высказывание на табличке первой двери:

Х = А \/ В

Высказывание на табличке второй двери:

Y = ¬A

Таблички либо обе истинны, либо обе ложны:

(X & Y) \/ (¬X & ¬y) = 1

Используя логические законы преобразуем выражение:

((A \/ B) & ¬A) \/ (¬(A \/ B) & ¬(¬A)) =

= (A & ¬A \/ B & ¬A) \/ (¬A & ¬B & A) =

= (0 \/ B & ¬A) \/ (¬A & A & ¬B) =

= (0 \/ B & ¬A) \/ (0 \/ ¬B) =

= (0 \/ B & ¬A) \/ 0 = B & ¬A = 1

Для выполнения этого равенства нужно, чтобы и В, и ¬А были равны 1.

Ответ : в первой аудитории находится кабинет физики, а во второй – кабинет информатики.