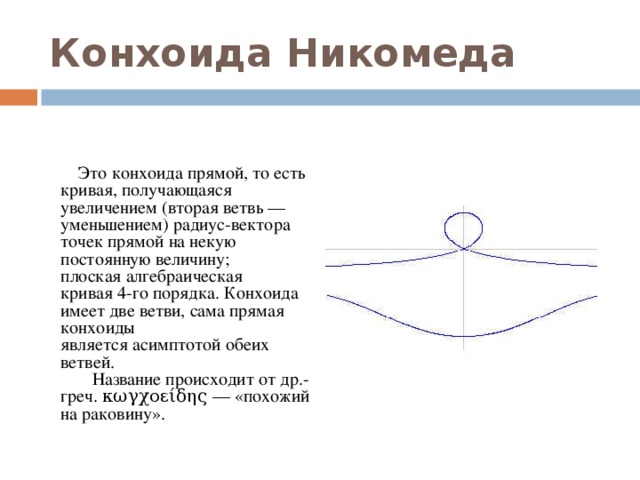
Это конхоида прямой, то есть кривая, получающаяся увеличением (вторая ветвь — уменьшением) радиус-вектора точек прямой на некую постоянную величину; плоская алгебраическая кривая 4-го порядка. Конхоида имеет две ветви, сама прямая конхоиды является асимптотой обеих ветвей.
Название происходит от др.-греч. κωγχοείδης — «похожий на раковину».
Просмотр содержимого документа
«Открытие Конхоиды Никомеда»

ОТКРЫТИЕ КОНХОИДЫ НИКОМЕДА
2016г

Никомед, древнегреческий математик
Никомед жил около 150 г. до Р. Х. Принадлежал к числу ученых, работавших в указанной исследованиями Архимеда области изучения высших кривых, в которой получил известность открытием конхоиды, т. е. кривой, представляющей геометрическое место точек, расстояния которых от данной прямой, считаемые по прямым, проходящим через данную точку, имеют постоянную длину. Никомед устроил также очень простой прибор для построения конхоиды непрерывным движением и приложил ее к остроумному решению задач о построении двух средних пропорциональных между двумя данными прямыми и о делении угла на 3 равные части.
Конхоида Никомеда
Это конхоида прямой, то есть кривая, получающаяся увеличением (вторая ветвь — уменьшением) радиус-вектора точек прямой на некую постоянную величину; плоская алгебраическая кривая 4-го порядка. Конхоида имеет две ветви, сама прямая конхоиды является асимптотой обеих ветвей. Название происходит от др.-греч. κωγχοείδης — «похожий на раковину».

Построение
Пусть на плоскости выбрана прямая m и точка O, отстоящая от прямой на расстояние a. Проведём через точку O луч, пересекающий прямую m в некоторой точке N; точки M1 и M2, лежащие на луче ON и отстоящие от точки N на заранее выбранное расстояние l, будут точками конхоиды. Меняя направление луча ON, можно построить всю конхоиду

Уравнения
- Уравнение в декартовых координатах:
- Полярное уравнение:
- Асимптота: y = a .

Задача о трисекции угла с помощью конхоиды по методу Никомеда:
Допустим, дан угол АО D ,
который необходимо разделить
на три части. Проведем через
точку А прямую L, параллельную
О D . Построим окружность W с центром в
точке А и R = a = ОА. Теперь построим конхоиду по
прямой L, точке О и числу а - она будет пересекаться с
окружностью W в точке C.
Полученный угол СО D = 1/3 АО D .






















