Открытый урок на тему:
«Метод подстановки»
7 класс
Конспект урока по алгебре в 7 классе на тему:
«Метод подстановки»
Цель урока: формирование у учащихся умения решать системы линейных уравнений с двумя неизвестными способом подстановки.
Образовательные: обобщение и систематизация знаний и умений учащихся при решении систем линейных уравнений с двумя переменными.
Развивающие: развитие математического и общего кругозора, мышления и речи учащихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.
Воспитательные: воспитание интереса к математике, активности, общей культуры, организованности и взаимопомощи через работу в парах.
Методы: частично – поисковый, коллективный, индивидуальный.
Тип урока: урок открытия новых знаний
Оборудование: раздаточный материал.
Литература: Учебник Макарычев Ю.Н. Алгебра 7. Издательство «Мнемозина»
| № | Этап урока | Время | Задачи этапа |
| 1. | Организационный момент | 1 мин.
|
|
| 2. | Проверка домашнего задания | 3 мин.
| Проверка правильности выполнения домашнего задания. |
| 3. | Актуализация опорных знаний учащихся | 5 мин. | Повторить основные определения; активизировать осознанность применения знаний при решении задач. |
| 4. | Изучение нового материала | 15 мин. | Знакомство учащихся с алгоритмом решения системы двух уравнений с двумя переменными методом подстановки (обратить внимание на оформление решений) |
| 6. | Закрепления изученного материала | 15 мин. | Сформировать умение решать системы уравнений методом подстановки |
| 7. | Домашнее задание | 2 мин. | Инструктаж по домашнему заданию |
Ход урока:
Этап №1. Организационный момент:
-Здравствуйте, садитесь,
Один из великих философов сказал: «ГДЕ ЕСТЬ ЖЕЛАНИЕ, НАЙДЕТСЯ ПУТЬ!». Я думаю, что сегодня на уроке мы с большим желанием будем решать системы, и не просто решать, а определяя свой рациональный путь.
Как вы справились с домашним заданием? Есть вопросы? Давайте проверим ответы, и вы поставите себе балл.
На прошлом уроке мы с вами познакомились с новой математической моделью.
Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными.
Ответим на несколько вопросов:
Этап №2. Теоретический опрос (устно)
1. что такое решение системы? (это пара значений, которая одновременно является решением всех уравнений системы)
2. что означает решить систему уравнений? (значит найти все её решения или установить, что их нет)
3. Является ли решением системы
пара чисел: а) х=3, у=1
б) х=2, у=2 ?
-
Раскрыть скобки -2(х-3)= -2х+6
2) Выразить у через х
х+у=3 у=3-х
3) Выразить х через у
2х-у=4 х=2+0,5у
4) Решить уравнение
2х-8=1
Этап №3. Актуализация опорных знаний
-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).
Алгоритм графического способа:
-
Построить графики каждого из уравнений системы.
-
Найти координаты точки пересечения построенных прямых (если они пересекаются)
-
Графический способ удобен, для определения количества корней системы уравнений.
Практическое задание:
Решить систему уравнений графическим способом (работаем в парах).


y=-x+3 y=2x-3
y=0,5x+2 y=0,5x-1
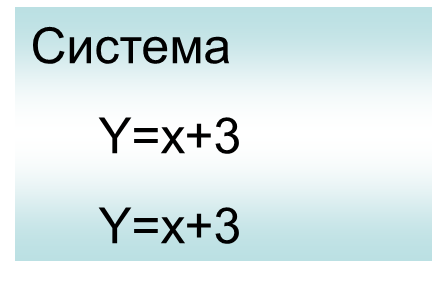
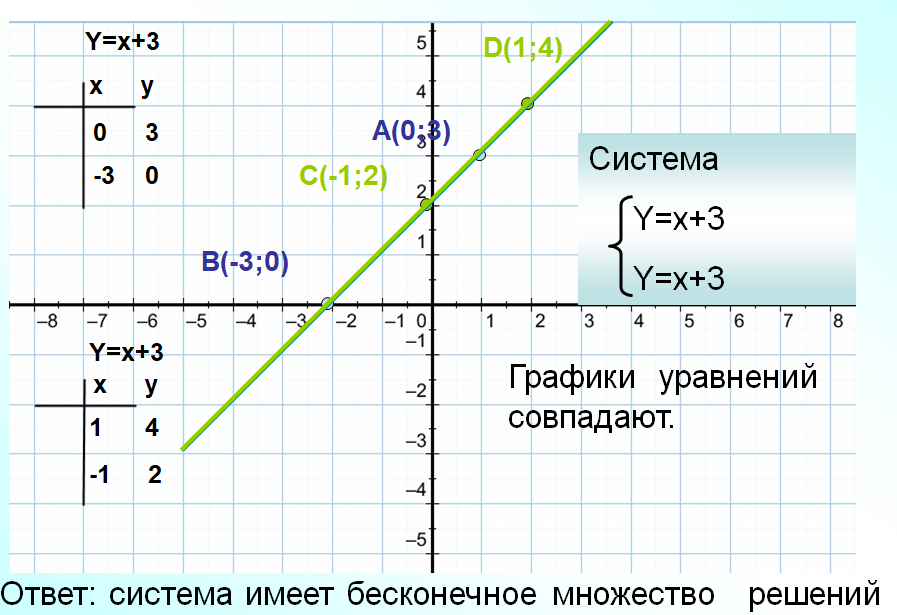
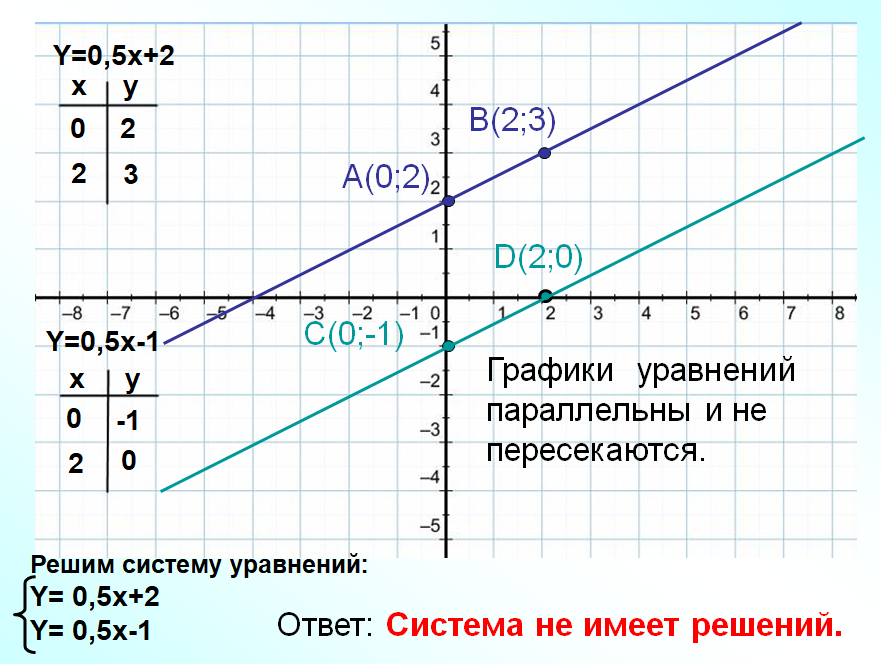
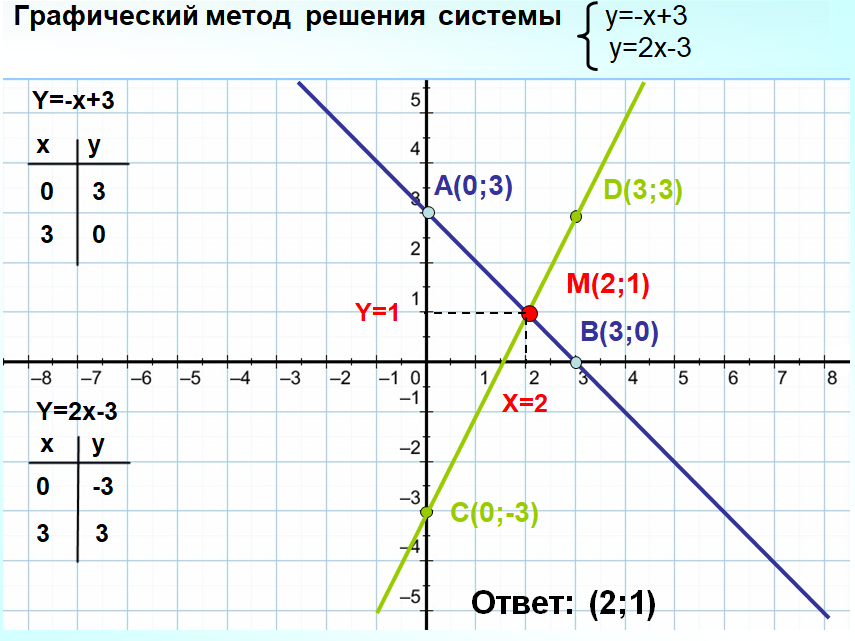
Задания делают на заранее приготовленных листах А4 с клетками, чтобы потом вывесить на доску, сравнить результаты и установить проблему урока.
Вывод:
Для решения данных систем уравнений графический способ не удобен. Решением первой системы являются дробные числа, которые трудно определить по графику. Решением второй системы являются большие числа, для определения которых не достаточно тетради.
Таким образом, необходим другой способ решения систем уравнений, который нас не подведет в случае с дробными значениями координат точки.
Этим мы и займемся сегодня на уроке
Этап №4
-В тетрадях запишите, пожалуйста, число.
Тема урока: «Метод подстановки».
Как вы думаете, какова цель нашего урока?
- узнать новый метод
- получить алгоритм решения систем
- научиться применять алгоритм
Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках. Итак:
№1. Выразить переменную У через Х в следующих уравнениях: (К доске пойдет…)
(Вызвать к доске ученика, задание на доске, следить за устной речью ученика, ученик комментирует свое решение)
5х-2у=0,
3х+2у=16
Ответ: у=2,5х у=8-1,5.
№2. На доске приведено, объяснено решение системы двух линейных уравнений с двумя переменными методом подстановки.
Затем еще 2 примера и дети составляют алгоритм.
Составим алгоритм по ключевым словам:
- выразим
- подставим
- решим
- подставим
- ответ
В учебнике найдите алгоритм решения и внимательно прочитайте его (стр. 212).
-Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.
Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.
Работа в парах
Сейчас мы с вами будем работать в парах: Решаем №1069,1068 в тетрадях с подробным объяснением, а затем сверимся с решением у доски (один человек работает у доски).
Рефлексия:
Обратите внимание на доску. В начале урока мы с вами записали цели урока. Добились ли мы цели? Решили ли проблему? Чем будем заниматься на следующих уроках?
Шёл мудрец, а навстречу ему три человека, везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: - Что ты делал целый день?
И тот с ухмылкою ответил, что целый день возил проклятые камни.
У второго спросил: «А ты что делал целый день?» - И тот ответил: «Я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием, и он ответил: «А я принимал участие в строительстве Храма». 
-Ребята! Кто работал так как первый человек? (поднимаем желтые)
-Кто работал добросовестно? (зелёные )
-А кто принимал участие в строительстве Храма знаний? (красные
Этап № 5.
Итог урока – Домашнее задание: знать алгоритм (стр. 211-212), № 1069 (д, г, е, б), № 1070(в, г).
Оценки сегодня получили… Спасибо за урок. До свидания.