Открытый урок по геометрии в 10 классе:"Призма".

МОУ «Октябрьская средняя общеобразовательная школа»

Томского района

Учитель-предметник: Куц Евгения Александровна

Урок по теме: “Призма. Свойства призмы».

Цель урока:

• Ввести понятие призмы, ее элементов;

• Знакомство с формулами вычисления площади поверхности призмы;

• формировать умение учащихся применять теоретический материал к решению задач;

• развивать пространственное и конструктивное мышление;

• формировать умение брать ответственность за выбор и проявлять самостоятельность при решении возникших проблем;

• воспитывать аккуратность чертежах, четкое оформление решений задач, положительный интерес к изучению математики, самостоятельности, инициативности учащихся на уроке.

Тип урока: изучение нового материала, систематизация знаний и умений учащихся.

Оборудование:

• классная доска;

• модели призм;

• компьютер, мультимедийный проектор, экран.

Межпредметные связи: черчение, русский язык.

ХОД УРОКА

I. План урока.

1.Фронтальный опрос
2. Новая тема.
3. Решение задач.
4. Подведение итогов.
5. Домашнее задание.

II. Организационный момент

Учитель проверяет готовность учащихся к уроку и объявляет тему урока «Призма и ее свойства». Учитель сообщает учащимся, что после рассмотрения теоретического материала, будет идти отработка его на решение задач.

III. Актуализация опорных знаний

Фронтальный опрос учащихся

1. Что такое многогранник?

2. Какие элементы содержит многогранник?

3. Что такое поверхность многогранника?

4. Что значит Эйлерова характеристика?

5. Какой угол называется плоским?

6. Чему равна сумма всех плоских углов в многограннике?

Изучение новой темы

Актуализация знаний и введение нового материала в форме фронтальной работы с классом.

Сегодня на уроке мы будем знакомиться еще с одним видом многогранника – это «Призма».

Мозговой штурм: «Ваши ассоциации со словом призма?» (записываются на доске варианты ответов учащихся).

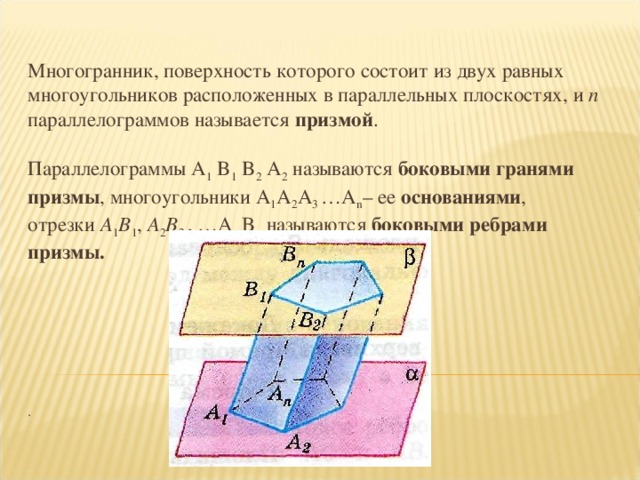
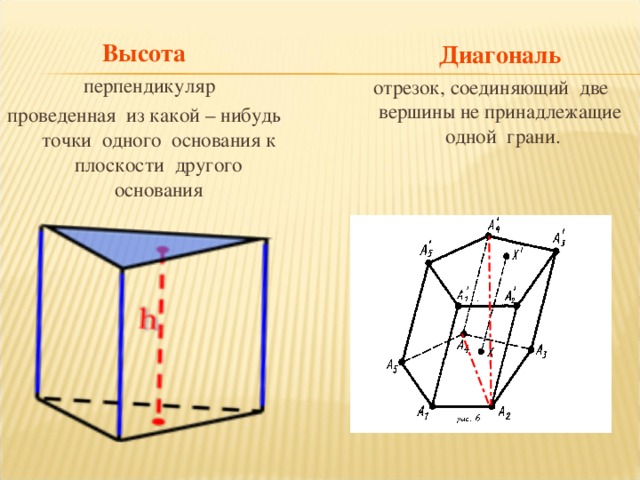
1. Дается определение призме с математической точки зрения, вводится понятие боковой грани, основанию и ребра призмы. (Слайд 1). Так же рассматриваем элементы призмы: высота и диагональ. (Слайд 2).

2. Рассматривая элементы призмы нельзя не обратить на свойства этой фигуры Предложить учащимся самим установить свойства призмы и затем обобщить их используя. (Слайд 4)

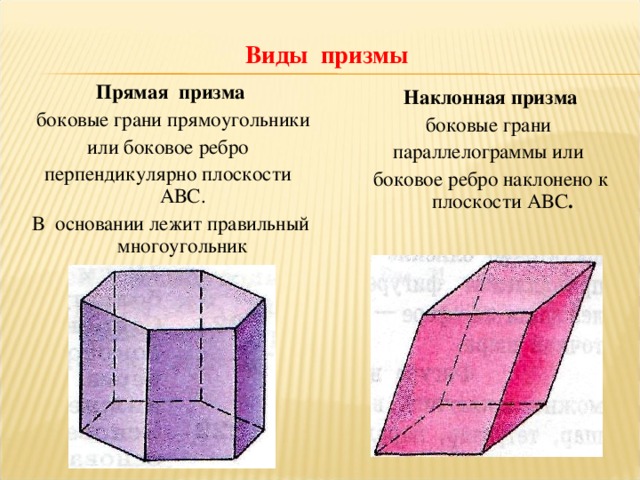
3. При помощи подвижной модели призмы знакомимся с видами призмы, выясняем их отличия друг от друга. Даем определение каждому виду призмы. (Слайд 3)

4. Предложить учащимся ответить на вопрос: Что собой представляет развертка призмы. Выслушав ответы, рассмотреть готовый чертеж развертки призмы.

(Приложение 1)

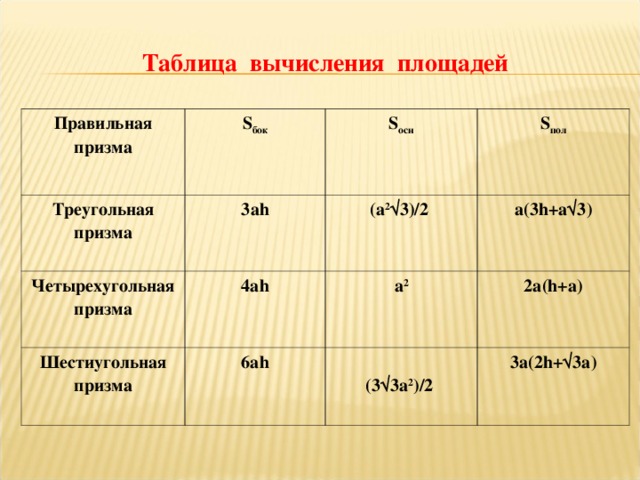
1. Вместе с учащимися знакомимся в формулами, площади боковой поверхности и полной поверхности призмы, так же и для разных видов призм. (Слайд 5)

(Слайд 6).

Закрпление нового материала

1. Устная работа.

а) Что называется призмой, боковыми гранями, основанием, высотой и диагональю призмы?

б) Что называется площадью боковой поверхности призмы, площадью полной поверхности призмы?

1. Решение задач.

№ 222 решают ученики у доски, № 229 (б,в) учащиеся решают самостоятельно, № 224 по готовому чертежу.

№ 222

Основанием прямой призмы является равнобедренная трапеция с основанием 25 см и 9 см и высотой 8 см. Найдите двугранные уголы при боковых ребрах призмы.

Дано: Решение:

АВСDА₁В₁С₁D₁ – прямая призма;

АВСD – р/б трапеция,

ВС = 25 см

АВ = DС

АD = 9см

АА₁= 8см.

Найти:

ВСС₁D -?

ВАА₁D -?

∟ВСD – линейный угол двугранного ∟ ВСС₁D, т.к. ВС┴ СС₁,

DС ┴ СС_1. Рассмотрим основание призмы АВСD, проведем высоты АК и DМ, ВК = МС, КМ = АД = 9 см.ВК + МС = 25 – 9 = 16 см, ВК = МС = 8 см

∆АВК = ∆DСМ, ∟ВСD = ∟СВА = 45⁰,

∟ВАD – линейный двугранный ∟ВАА₁D, т.к. АА₁ ┴ ВА, АА₁┴ АD.

∟ВАD = ∟СDА = 45⁰+ 90⁰ = 135⁰.

Ответ : 45⁰ и 135⁰

№ 226 (б)

В правильной n- угольной призме сторона основания равна а и высота равна h. Вчислите площади боковой и поной поверхности призмы, если: n = 4,

а = 12 дм, h = 8 дм.

Дано: Решение:

n = 4 S_бок = 4аh

а = 12 дм S_бок = 4· 8 · 12 = 384 (дм²)

h = 8 дм S_пол = 2S_осн + S_бок

Найти: S_осн = а² = 12² = 144 (дм²)

S_бок- ? S_пол= 2· 144 + 384 = 672 (дм²)

S_пол - ?

Ответ: 384 дм², 672 дм²

№ 226 (в)

В правильной n- угольной призме сторона основания равна а и высота равна h. Вчислите площади боковой и поной поверхности призмы, если: n = 6,

а = 23 дм, h = 5 дм.

Дано: Решение:

n = 6 S_бок = 6аh

а = 23 см S_бок = 6· 50 · 23 = 6900 (см²) = 69 (дм²)

h = 5 дм= 50 см S_пол = 3а·(2h + √3·а)

Найти: S_пол = 69·(100 + 23√3) = 69· 140 = 9660 (см²) = 97 (дм²)

S_бок- ?

S_пол - ?

Ответ: 69 дм², 97 дм²

№ 224

Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60⁰. Найдите площадь сечения, проходящего через сторону нижнего основания и противолежащую с торону верхнего основания, если диагональ основания равна

4 √2 см.

Дано:

АВСDА₁В₁С₁D₁ – правильная

четырехугольная призма;

∟В₁ DВ = 60⁰,

ВD = 4√2 см

Найти:

S_АDС1В1 - ?

Решение:

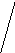
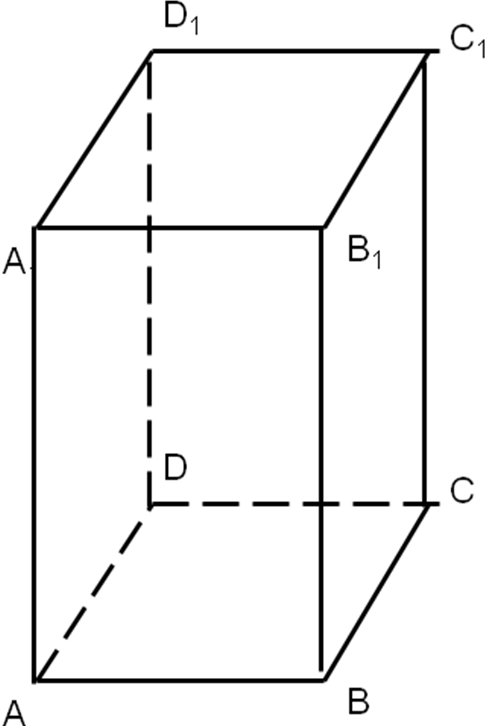
АDС₁ В₁ - прямоугольник,

АВС ┴ АD, В₁В┴ АD, по теореме о трех перпендикулярах АВ₁┴ АD, следовательно АВ₁ ┴ В₁С₁).

АВСD – прямоугольник:

АВ = ВD · sin 45⁰ = (4√2·2)/2 = 4√2

АD = 4

∆ВВ₁D: ВD ·tq 60⁰ = 4√2 · √3 = 4√6

∆DС₁С: DС₁= √16 + 64 = 4√7 см.

S_АDС1В = 4 · 4√7 = 16 √7 (см²).

Ответ: 16√7 см²

Подведение итогов урока: релаксация

Доммашнее задание: п. 27 - 31, № 220 и №229 (а, г)

Многогранник, поверхность которого состоит из двух равных многоугольников расположенных в параллельных плоскостях, и n параллелограммов называется призмой . Параллелограммы A 1 B 1 B 2 A 2 называются боковыми гранями призмы , многоугольники A 1 A 2 A 3 …A n – ее основаниями , отрезки A 1 B 1 , A 2 B 2, , …А n В n называются боковыми ребрами призмы. .

Высота

перпендикуляр

проведенная из какой – нибудь точки одного основания к плоскости другого основания

Диагональ

отрезок, соединяющий две вершины не принадлежащие одной грани.

Виды призмы

Прямая призма

боковые грани прямоугольники

или боковое ребро

перпендикулярно плоскости АВС.

В основании лежит правильный многоугольник

Наклонная призма

боковые грани

параллелограммы или

боковое ребро наклонено к плоскости АВС .

Свойства призмы.

1 . Основания призмы являются равными многоугольниками.

2. Боковые грани призмы являются параллелограммами.

3. Боковые ребра призмы равны.

4. Противоположные ребра параллельны и равны.

5. Все боковые ребра равны и параллельны.

6. Противоположные боковые грани равны и параллельны.

7. Высота перпендикулярна каждому основанию.

8. Диагонали пересекаются в одной точке и делятся в ней пополам.

Нахождение площади

• Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

S бок = P осн · h

P - периметр

h – высота призмы

• Площадь полной поверхности призмы называется сумма площадей всех ее граней.

S пол = S бок + 2 S осн

Таблица вычисления площадей

Правильная призма

S бок

Треугольная призма

3а h

S осн

Четырехугольная призма

Шестиугольная призма

S пол

( a 2 √ 3) /2

4ah

6ah

a (3 h + a√3 )

а 2

2a ( h + a )

(3 √ 3а 2 ) /2

3a ( 2h + √3a )

СПАСИБО ЗА УРОК !