| 3. Экскурсия по музею. Перед вами представлен первый экспонат, обратите внимание, он составлен из треугольников. В порядке очереди не повторяя друг друга прошу найти виды треугольников, дать им определение (р/б, р/с, прямоугольного, тупоугольного треугольника). Ребята, вы заметили сундук? Хотелось бы вам узнать, что хранится в нем? Нам необходим КОД, давайте его получим. Решите тест по теме «Равнобедренный треугольник», ответы необходимо записать в таблицу кодов. Проверяем! Сундук открыт, посмотрите, что хранится в нем… Китайский мудрец сказал: «Знания – это бесценное сокровище, которое повсюду следует за тем, кто им обладает». Предлагаю Вам пополнить знания о треугольниках. С исторических времен эта геометрическая фигура окружала и окружает нас, много интересных фактов связанные с треугольниками. У вас на столах лежат информационные листы, прошу в порядке очереди прочитать их. Ответы учащихся: Треугольником называется геометрическая фигура, состоящая из 3 точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки». Внешним углом треугольника называется угол, смежный с внутренним. Свойство: Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним». Виды треугольников: «Остроугольным треугольником называется треугольник, у которого все углы острые. Тупоугольным называется треугольник, у которого один угол тупой, а два других острые. Прямоугольным треугольником называется треугольник, у которого один угол прямой, а два других острые. Подробнее о прямоугольных треугольниках мы поговорим у стенда, посвященного прямоугольным треугольникам. Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья – основанием. У равнобедренного треугольника имеются следующие свойства: Углы при основании равны Медиана, проведённая к основанию, является биссектрисой и высотой. Аналогичным свойством обладают и высота, и биссектриса. Равносторонним треугольником называется треугольник, у которого все стороны равны. В равностороннем треугольнике каждый угол равен 60°. Каждая медиана является и биссектрисой и высотой, и все они пересекаются в одной точке. Равными называются треугольники, у которых соответствующие стороны и углы равны. Существует три признака равенства треугольников. О них подробнее мы узнаем у следующего стенда нашего музея».Продолжить ряд слов: Мы продолжаем экскурсию по музею, обратим внимание на 2 экспонат «Дерево треугольников» Данная композиция нам позволяет вспомнить названия сторон прямоугольного треугольника, замечательные свойства прямоугольного треугольника. Сколько признаков равенства существует для прямоугольных треугольников? Давайте назовем их: по двум катетам, по гипотенузе и острому углу, по катету и прилежащему острому углу, по катету и противолежащему острому углу, по гипотенузе и катету. В порядке очереди, без повторения, прошу найти пары равных треугольников и озвучить признак равенства. Какие замечательные свойства характерны для прямоугольного треугольника? Ответы учащихся: Сумма острых углов в прямоугольном треугольнике равна 90°. Гипотенуза больше каждого катета. Напротив угла в 30° лежит катет, равный половине гипотенузы. Если катет равен половине гипотенузы, то он лежит напротив угла 30°.
Сейчас, прошу вас решить задачи на эти замечательные свойства в рабочих листах под №2, ответы занести в таблицу. ФИЗМИНУТКА Мы продолжаем наше путешествие по музею, обратите внимание на данную композицию 3. «Фигуры из треугольников».  У вас на столах конверты с комплектом треугольников, попробуйте создать следующие экспонаты (кошку, рыбку, пароход, робота, бегущий человек), мы их передадим в музей геометрических фигур. (На формате А-4, ребята создают фигуру и прикрепляют на доску) Резерв. Всегда ли можно построить треугольник? У вас на столах набор отрезков, попробуйте построить треугольник. Обратимся к следующему экспонату «Треугольник в архитектуре». (Картинки) 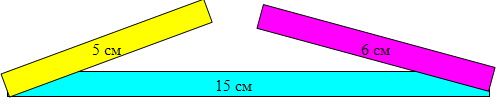 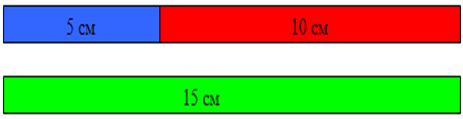 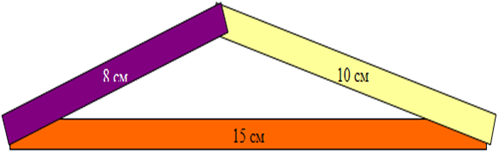 Какой мы сделаем вывод, наблюдая за данной композицией? «Итак, треугольник можно построить только в том случае, если выполняется одно важное условие: каждая сторона должна быть меньше суммы двух других сторон. А+В С А+С В С+В А совершенно верно! Прошу проверить в задании №3 какой из треугольников не существует, зачеркните его. | 




















