Открытый урок Симметрия.

ГБОУ СПО (ССУЗ) ЮУМК

Методическая разработка урока

СИММЕТРИЯ

Преподаватель: Костылева

Елена Владимировна

2014

Технологическая карта занятия № 141-142

Преподаватель: Костылева Е.В,

Дисциплина: Математика (геометрия)

Тема занятия: Симметрия

Тип занятия: Урок изучения нового материала.

Вид занятия: Урок – беседа с элементами исследования

Форма работы: Групповая, индивидуальная.

Цели занятия:

Дидактическая: Сформировать понятие симметрии в пространстве , изучить виды симметрии, научить находить симметричные объекты в окружающем мире. Дать представление о симметрии в математике, физике, биологии, искусстве. Осуществлять межпредметную связь. Отработать умение применять современные ИКТ для оформления результатов исследования.

Развивающая: Формировать навыки работы в команде. Воспитывать коммуникативность. Прививать культуру общения.

Воспитательная: Развивать познавательный интерес через творческую активность, исследовательскую деятельность. Способствовать формированию навыков работы с большими объемами информации, умений увидеть проблему и наметить пути ее решения. Развивать умение кратко излагать свои мысли устно и письменно.

Задачи занятия: познакомиться с осевой, центральной и зеркальной симметрией;

расширить свои представления о симметрии;

увидеть различные проявления симметрии в окружающем нас мире. сформировать пространственных представлений студентов;

развивать умения наблюдать и рассуждать;

воспитывать человека, умеющего ценить прекрасное.

Обеспечение занятия средствами обучения: Компьютер, экран, презентации в формате PowerPoint, карточки с практическими заданиями, карточки с домашним заданием.

ХОД И СОДЕРЖАНИЕ ЗАНЯТИЯ:

1. Организационный момент: Настрой на урок. Проверка готовности группы к уроку и приветствие всех присутствующих.

2. Сообщение темы и целей урока: Ознакомление с порядком проведения урока, рекомендации обучающимся, на что необходимо обратить особое внимание, что следует записать в рабочую тетрадь.

2.1 Преподаватель предлагает угадать тему урока, решив кроссворд

(слайд 2)

2.2 (слайд 3)

Симметрия! Гимн о тебе пою!

Тебя повсюду в мире узнаю.

Ты в Эйфелевой башне, в малой мошке,

Ты в елочке, что у лесной дорожки.

С тобою в дружбе и тюльпан, и роза,

И снежный рой – творение мороза!

3.Изучение нового материала:

3.1 Введение.

Что такое симметрия? Выдающийся математик Герман Вейль высоко оценил роль симметрии в современной науке: "Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство".

Мы живем в очень красивом и гармоничном мире. Нас окружают предметы, которые радуют глаз. Например, бабочка, кленовый лист, снежинка. Посмотрите, как они прекрасны. Вы обращали на них внимание? Сегодня мы с вами прикоснемся к этому прекрасному математическому явлению – симметрии. Познакомимся с понятием осевой, центральной и зеркальной симметрий. Будем учиться строить и определять симметричные относительно оси, центра и плоскости фигуры.

Слово “симметрия” в переводе с греческого звучит как “гармония”, означая красоту, соразмерность, пропорциональность, одинаковость в расположении частей. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.

запись в тетрадях: (слайд 4)

"Симметрия" – такое преобразование пространства (плоскости), при котором каждая точка M переходит в другую точку M₁ относительно некоторой плоскости (или прямой).

Плоскость (прямая) a называется при этом плоскостью (или осью) симметрии.

К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии.

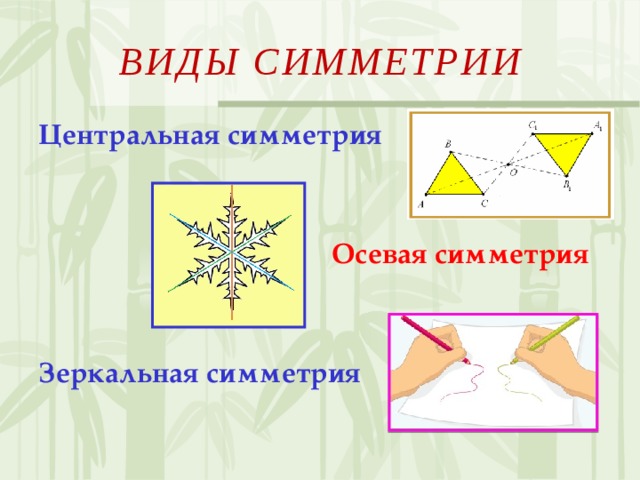
Виды симметрии: (слайд 5)

1. Центральная симметрия

2. Осевая симметрия

3. Зеркальная симметрия

3.2 Основная часть. Виды симметрии.

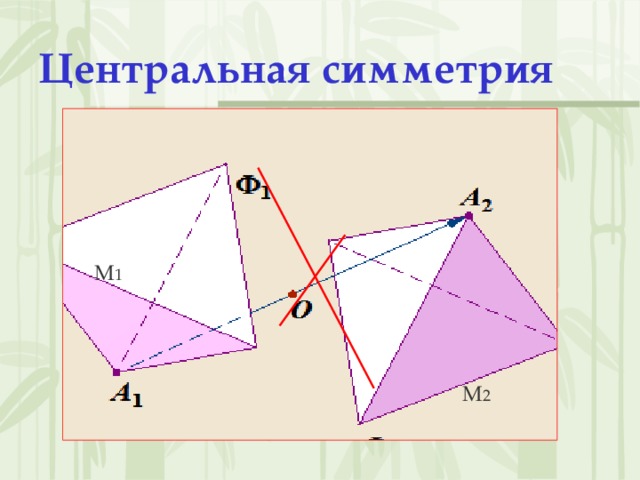
Центральная симметрия (слайд 6-7)

Симметрия относительно точки или центральная симметрия – это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам.

Практическое задание. (на доске) (слайд 8)

1. Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.

2. Построить фигуру, симметричную точке М (лист заданий)

3. Какие из следующих букв имеют центр симметрии: А, О, М, Х, К?

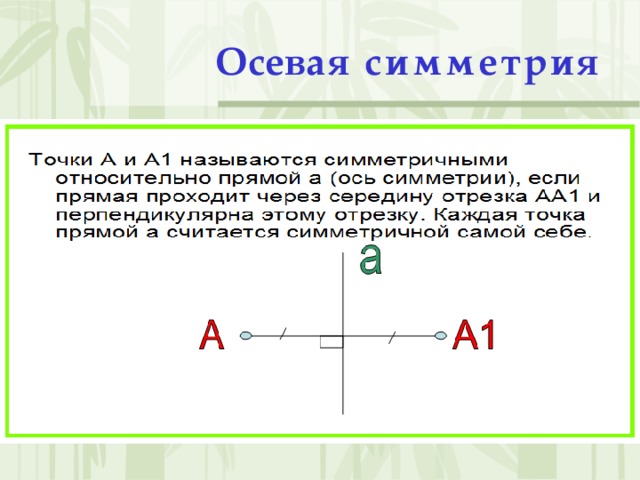
Осевая симметрия (слайд 9)

Симметрия относительно прямой (или осевая симметрия) – это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам.

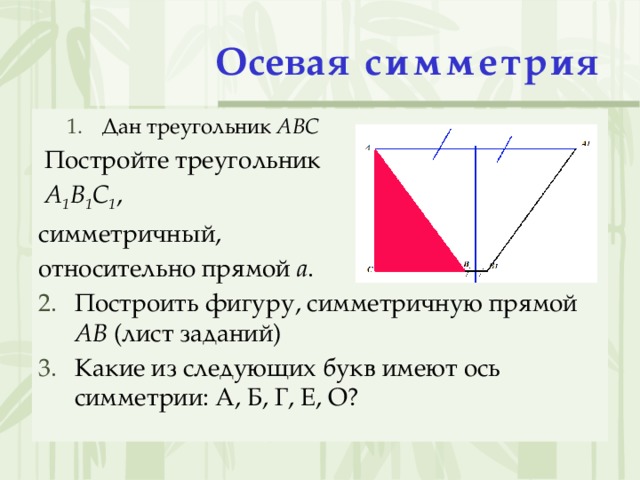
Практическое задание. (слайд 10)

1. Дан треугольник АВС Постройте треугольник А₁В₁С₁, симметричный относительно прямой а.

1. Построить фигуру, симметричную прямой АВ (лист заданий)

1. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О?

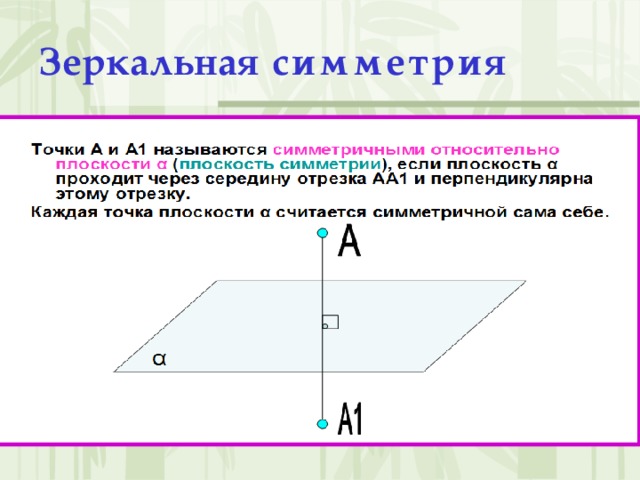
Зеркальная симметрия (слайд 11)

Точки А и В называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АВ и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной сама себе.

Практическое задание. (слайд 12)

1. В правую или левую перчатку переходит правая перчатка при зеркальной симметрии? осевой симметрии? центральной симметрии?

2. Видим ли мы себя в зеркале?

3. На рисунке показано, как слово КЕНГУРУ отражается в двух зеркалах. Что получится, если то же самое проделать с числом 2011?

4. Первичное закрепление и применение полученных знаний.

Тестирование

1. На рисунке точки А₁ и А₂ симметричны относительно…

а) точки

б) прямой

в) плоскости

2. Какие из геометрических фигур не являются симметричными?

а) квадрат

б) равнобедренный треугольник

в) прямоугольный треугольник

3. Какие фигуры являются симметричными?

а) б) в)

4. В координатной системе прямые x, y, z являются

а) координатными осями

б) координатными плоскостями

в) началом координат

1. На рисунке точки А₁ и А₂ симметричны относительно…

а) точки

б) прямой

в) плоскости

6. Какой вид симметрии изображен на рисунке?

а) центральная симметрия

б) осевая симметрия

в) зеркальная симметрия

1. Изучение нового материала

Симметрия вокруг нас (слайд 13)

Каков он наш мир? Обычно говорят: огромный, прекрасный, разнообразный…

Красота и разнообразие реальных объектов непосредственно связаны с такими их свойствами, как симметричность, то есть правильность, упорядоченность, повторяемость, гармония, и, наоборот, асимметричность – неправильность, нарушение порядка.

Сочетание симметричности и асимметричности создает основу эстетического восприятия человеком природы и произведения искусства.

Вопрос: А где вы встречались с симметрией в жизни? Где в повседневной жизни вы с ней сталкивались? (Приведите примеры)

Симметрия широко распространена в природе. Так же издавна человек использовал симметрию в архитектуре. Однако симметрия существует и там, где ее не видно на первый взгляд. Физик скажет вам, что всякое твердое тело – это кристалл. Химик скажет, что все тела состоят из молекул, а молекулы состоят из атомов. А многие атомы располагаются в пространстве по принципу симметрии.

Луи Пастер полагал, что симметрия - страж покоя, а асимметрия - двигатель жизни.

Давайте рассмотрим некоторые проявления симметрии в нашей жизни

Симметрия в природе. (слайд 14-15)

Симметрия широко встречается в объектах живой и неживой природы. "Зеркальной" симметрией обладает бабочка, листок или жук) и часто такой вид симметрии называется "симметрией листка" или "билатеральной симметрией".

Животный мир и симметрия. На плоскости существует два вида симметрии: осевая и центральная. Симметрию живого существа определяет направление его движения. Для живых существ, для которых ведущим направлением является направление движения “вперед”, наиболее характерна осевая симметрия. Так как в этом направлении животные устремляются за пищей и в этом же спасаются от преследователей. А нарушение симметрии привело бы к торможению одной из сторон и превращению поступательного движения в круговое. Центральная симметрия чаще встречается в форме животных, обитающих под водой.

Симметрия в архитектуре и искусстве. (слайд 16-17)

Прекрасные образцы симметрии демонстрируют произведения архитектуры, которые сопровождают человечество на всем его историческом пути. Симметричные объекты обладают большей устойчивостью и равной функциональностью в разных направлениях. Все это привело человека к мысли о том, что, чтобы сооружение было красивым, оно должно быть симметричным.

Симметрия в буквах и словах (слайд 18-19)

Буквы А, М, Т, Ш, П имеют вертикальную ось симметрии, В, З, К, С, Э, В, Е – горизонтальную. А буквы Ж, Н, О, Ф, Х имеют по две оси симметрии. Симметрию можно увидеть и в словах: КАЗАК, ШАЛАШ.

Слова или фразы, которые можно прочитать, как слева направо, так и справа налево называют

Палиндром (греч.) – перевёртыш.(Palindromeo-бегу назад)

Вы все наверняка помните книгу о приключениях Буратино. А помните , как строгая Мальвина учила его писать ?

Она велела ему записать такую фразу :

А РОЗА УПАЛА НА ЛАПУ АЗОРА,

А потом прочитать её «наоборот».

ещё несколько фраз-палиндромов:

Осело колесо,

Я не стар брат сеня

Я ем змея

А собака боса

Аргентина манит негра

Искать такси

Ценит негра аргентинец

Лёша на полке клопа нашёл

А ещё мы обнаружили слова-палиндромы:

Шалаш,

наган,

казак,

кок

Попробуйте и вы вспомнить или придумать слова или фразы – палиндромы Композитор Иоганн –Себастьян Бах является автором музыкального палиндрома .Его произведение звучит одинаково при чтении слева направо и наоборот. Есть слова палиндромы и в иностранных языках.

Но оказывается и среди чисел есть палиндромы. (слайд 20-21)

Более того, все двузначные числа дают палиндромы ( наибольшего числа шагов – 24- требуют числа 89 и 98).

Пример 1.

Возьмём число 619

Прочитаем его

1 шаг справа налево 916

Сложим два числа 1535

«перевернём» 5351

2 шаг Сложим 6886

Число 6886 – палиндром. Причём полученное, всего за 2 шага. Читая его справа налево или слева направо, получим то же самое число. Кстати, оно имеет вертикальную симметрию.

Пример 2.

Возьмём число 95

1 шаг.

«Перевернём» 59

Сложим 154

2 шаг.

«Перевернём» 451

Сложим 605

3 шаг

«Перевернём» 506

Сложим 1111

Число 1111 – палиндром.

Между прочим, нашему поколению выпала большая удача,

не каждому человеку выпадает прожить хотя бы

один палиндромный год, а уж тем более два – 1991-й и 2002-й.

Ведь предыдущий был в 1881-м, а следующий — в 2112-м

А уж миг полного числового равноденствия палиндромный миг

20.02 2002 20.02 приходит и того реже…

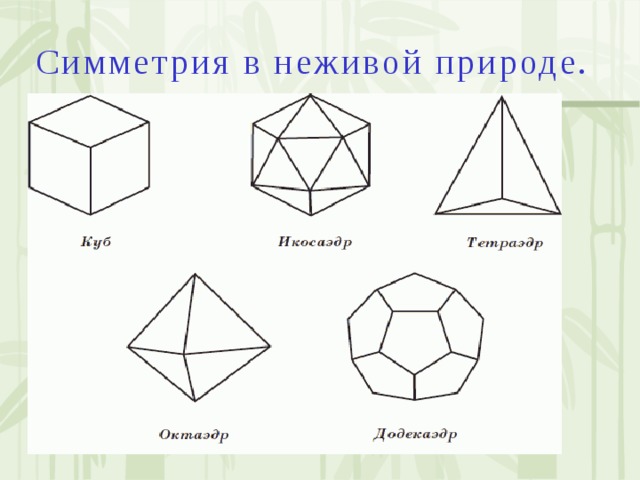
Симметрия в неживой природе. (слайд 22-23)

Среди бесконечного разнообразия форм неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. Наблюдая за красотой природы, можно заметить, что при отражении предметов в лужах, озерах проявляется зеркальная симметрия

В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают поворотной симметрией и, кроме того, зеркальной симметрией, и имеют по 6 осей симметрии.

Нельзя не увидеть симметрию и в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра.

Симметрия в технике. (слайд 24-25)

Еще одним примером использования человеком симметрии в своей практике – это техника. В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Или одно из важнейших изобретений человечества, имеющих центр симметрии, является колесо, также центр симметрии есть у пропеллера и других технических средств.

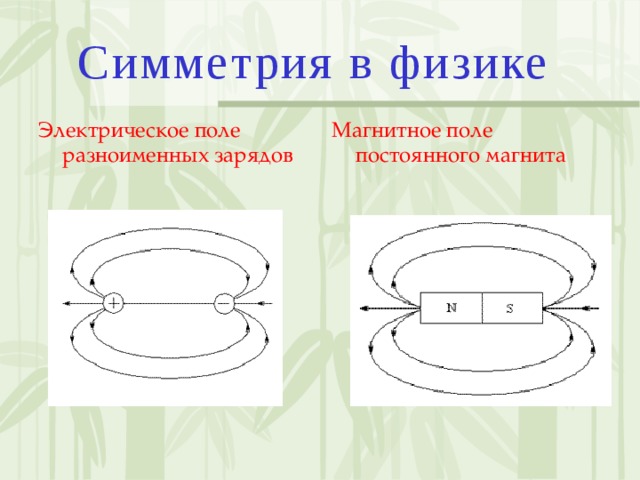
Симметрия в физике. (слайд 26-27)

Физические явления и процессы подтверждают понятие геометрической симметрии.

Внешне симметрию подтверждает картина силовых линий электрического и магнитного полей

Магнитное поле постоянного магнита Электрическое поле разноименных зарядов

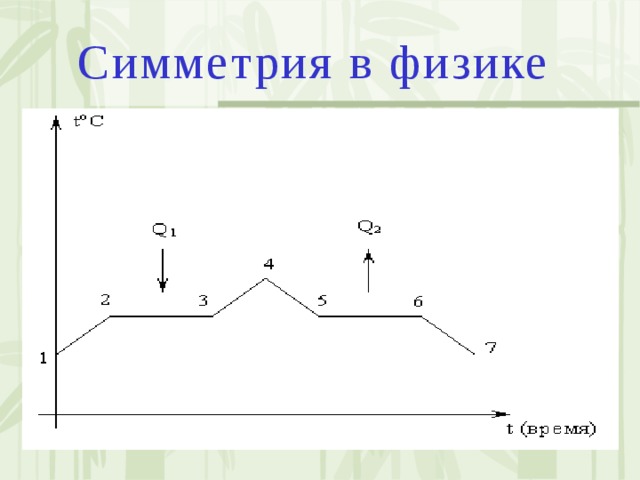
Рассмотрим фазовые переходы I рода кристаллическое тело – жидкость – кристаллическое тело, используя график плавления и кристаллизации.

1-2 — нагревание твёрдого тела,

2-3 начинается разрушение кристаллической решётки и заканчивается. Нагревания не происходит.

3-4 — нагревание жидкости.

Затем начинается обратный процесс.

Попробуйте закончить описание процесса самостоятельно.

Т.е., мы видим геометрическую симметрию, изображённую с помощью графика плавления, а сами фазовые переходы, как физические процессы, подсказывают о негеометрической симметрии — симметрии взаимодействий физических процессов.

1. Закрепление изученного материала. (слайд 28)

1.С какими видами симметрии вы познакомились на уроке?

2.Приведите примеры фигур, обладающих:

а) осевой симметрией; б) центральной симметрией; в) и осевой, и центральной симметрией.

Домашнее задание

1. Подготовить мини – проект

«Симметрия в природе»,

«Симметрия в технике»,

«Симметрия в моей профессии»

1. Решите кроссворд:

Вопросы к кроссворду:

1. Слово «Симметрия» - в узком смысле слова.

2. Тема, которую мы изучаем.

3. Ученый, который впервые ввел в элементарную геометрию элементы учения о симметрии.

4. Симметрия относительно прямой.

5. Прямая, при перегибании по которой «половинки» совпадут.

6. Точка, относительно которой фигуры симметричны.

7. Основное свойство симметрии, при котором фигуры …

8. Симметрия относительно точки.

9. Симметрия относительно плоскости.

10. Еще один вид симметрии, о котором мало упоминают.

Ответы к кроссворду

1. Соразмерность

2. Симметрия

3. Лежандр

4. Осевая

5. Ось

6. Центр

7. Равны

8. Центральная

9. Зеркальная

10. Поворотная

Рефлексия (слайд 29-30)

Гармония чисел, гармония линий,

Мира гармонию вы повторили.

Строгая логика – щит от разлада,

Кружево формул – сердцу награда.

Но путь к ней неровен – от впадин до всплесков,

Мрачен, иль светится солнечным блеском.

К тайнам извечным разум влекущий,

Тот путь бесконечный, осилит идущий

Выберите, пожалуйста, один из вариантов ответа в каждой строке

СИММЕТРИЯ

Симметрия! Гимн о тебе пою!

Тебя повсюду в мире узнаю.

Ты в Эйфелевой башне, в малой мошке,

Ты в елочке, что у лесной дорожки.

С тобою в дружбе и тюльпан, и роза,

И снежный рой – творение мороза !

СИММЕТРИЯ

Такое преобразование пространства

(плоскости), при котором каждая точка M переходит в другую точку M 1 относительно некоторой плоскости (или прямой).

Плоскость (прямая) a называется при этом плоскостью (или осью) симметрии.

Фундаментальные понятия симметрии:

плоскость симметрии,

ось симметрии,

центр симметрии.

ВИДЫ СИММЕТРИИ

Центральная симметрия

Осевая симметрия

Зеркальная симметрия

Центральная симметрия

Центральная симметрия

М 1

М 2

Центральная симметрия

• Даны точки А , В и М . Постройте точку, симметричную точке М относительно середины отрезка АВ .

• Построить фигуру, симметричную точке М (лист заданий)

• Какие из следующих букв имеют центр симметрии: А, О, М, Х, К?

Осев ая симметрия

Осев ая симметрия

• Дан треугольник АВС
• Дан треугольник АВС

Постройте треугольник

А 1 В 1 С 1 ,

симметричный,

относительно прямой а .

• Построить фигуру, симметричную прямой АВ (лист заданий)
• Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О?

Зеркальная симметрия

Зеркальная симметрия

• В правую или левую перчатку переходит правая перчатка при зеркальной симметрии? осевой симметрии? центральной симметрии?
• Видим ли мы себя в зеркале?
• На рисунке показано, как слово КЕНГУРУ отражается в двух зеркалах. Что получится, если то же самое проделать с числом 2011?

Симметрия вокруг нас

Симметрия в природе .

Симметрия в природе .

Симметрия в архитектуре и искусстве.

Симметрия в архитектуре и искусстве.

А М Т Ш П

(вертикальная ось симметрии )

В З К С Э Е

(горизонтальная ось симметрии)

Ж Н О Ф Х

(И центральная и осевая симметрия)

Б; Г; И; Й; Р; У; Ц; Ч; Щ; Я

(ни вертикальные, ни горизонтальные оси)

Палиндромы

Фразы

Осело колесо,

Я не стар брат Сеня

А собака боса

Аргентина манит негра

Искать такси

Лёша на полке клопа нашёл

Слова

Шалаш,

наган,

казак,

кок

Палиндромы в математике

Пример 1.

Возьмём число 619

Прочитаем его справа налево 916

Сложим два числа 1535

«перевернём» 5351

Сложим 6886  

Число 6886 – палиндром. Причём полученное, всего за 2 шага. Читая его справа налево или слева направо, получим то же самое число. Кстати, оно имеет вертикальную симметрию.

Палиндромы в математике

Пример 2.

Возьмём число 95

«Перевернём» 59

Сложим 154

«Перевернём» 451

Сложим 605

«Перевернём» 506

Сложим 1111

Число 1111 – палиндром.

Симметрия в неживой природе.

Симметрия в неживой природе.

Симметрия в технике.

Симметрия в технике.

• к

• А 1

• А

• m

• А 2

Решение

к

А 1

А

m

А 2

25

Симметрия в физике

Электрическое поле разноименных зарядов

Магнитное поле постоянного магнита

Симметрия в физике

Закрепление изученного материала.

1.С какими видами симметрии вы познакомились на уроке?

2.Приведите примеры фигур, обладающих:

а) осевой симметрией;

б) центральной симметрией;

в) и осевой, и центральной симметрией .

Рефлексия

Гармония чисел, гармония линий,

Мира гармонию вы повторили.

Строгая логика – щит от разлада,

Кружево формул – сердцу награда.

Но путь к ней неровен – от впадин до всплесков,

Мрачен, иль светится солнечным блеском.

К тайнам извечным разум влекущий,

Тот путь бесконечный, осилит идущий

Выберите, пожалуйста, один из вариантов ответа в каждой строке

На уроке я работал

активно / пассивно

Своей работой на уроке я

доволен / не доволен

Урок для меня показался

коротким / длинным

За урок я

устал / не устал

стало лучше / стало хуже

Мое настроение

понятен / не понятен

Материал урока мне был

полезен / бесполезен

интересен / скучен

легким / трудным

Домашнее задание

интересно / не интересно

Спасибо

За

Урок!