Просмотр содержимого документа
«Памятка. Пределы, неопределенности»
Памятка: Предел, виды неопределенностей


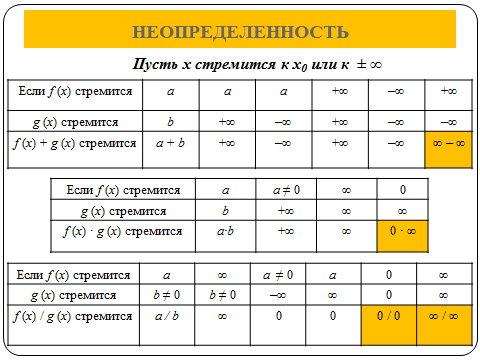
 1. Если находим предел дробного выражения, в числителе и знаменателе которого многочлен и имеем неопределенность 0 / 0, то для раскрытия данной неопределенности:
1. Если находим предел дробного выражения, в числителе и знаменателе которого многочлен и имеем неопределенность 0 / 0, то для раскрытия данной неопределенности:
а) числитель и знаменатель дроби разлагаем на множители;
б) сокращаем на критический множитель;
в) вычисляем предел.
2. Если находим предел дробно-иррационального выражения и имеем неопределенность 0 / 0, то для раскрытия данной неопределенности: а) умножаем числитель и знаменатель дроби на сопряженное выражение;
б) применяем формулу разности квадратов (суммы и разности кубов);
в) сокращаем на критический множитель;
 г) вычисляем предел.
г) вычисляем предел.
3. Если находим предел дробного выражения в числителе и знаменателе которого могут встречаться тригонометрические, обратные тригонометрические, показательные, логарифмические функции и имеем неопределенность 0 / 0, то для раскрытия данной неопределенности:
 а) воспользуемся таблицей эквивалентных БМФ; б) сокращаем на критический множитель;
а) воспользуемся таблицей эквивалентных БМФ; б) сокращаем на критический множитель;
 в) вычисляем предел
в) вычисляем предел

Сравнение
порядка роста функции

8. Неопределённость ∞ - ∞ устраняется
3-мя распространёнными способами:
 а) приведением выражения под знаком предела к общему знаменателю;
а) приведением выражения под знаком предела к общему знаменателю;
б) умножением/делением на сопряжённое выражение;
в) преобразованием логарифмов.
Замечательные пределы: I 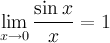 1°
1° 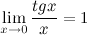 2°
2° 
I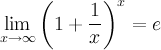 I 3°
I 3° 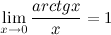 4°
4° 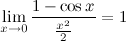
1°  2°
2° 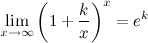 3°
3° 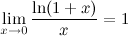 4°
4° 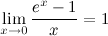
5° 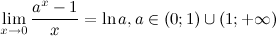 6°
6° 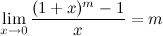
Правило Лопиталя. Пусть функции 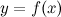 и
и 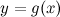 удовлетворяют
удовлетворяют
следующим условиям:
1) эти функции дифференцируемы в окрестности точки  , кроме, может быть, самой точки
, кроме, может быть, самой точки  ;
;
2
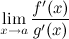
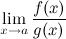 ) g(x) ≠ 0 и gˈ(x) ≠0 в этой окрестности; 3) ; 4) сущ. конечный или бесконечный
) g(x) ≠ 0 и gˈ(x) ≠0 в этой окрестности; 3) ; 4) сущ. конечный или бесконечный
Т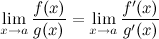 огда существует и , причем
огда существует и , причем
P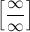 S: не распространяется на при
S: не распространяется на при 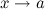 Доп.формула:
Доп.формула: 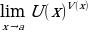 =
= 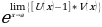 Волошина Н.Н.
Волошина Н.Н.










 1. Если находим предел дробного выражения, в числителе и знаменателе которого многочлен и имеем неопределенность 0 / 0, то для раскрытия данной неопределенности:
1. Если находим предел дробного выражения, в числителе и знаменателе которого многочлен и имеем неопределенность 0 / 0, то для раскрытия данной неопределенности: г) вычисляем предел.
г) вычисляем предел. а) воспользуемся таблицей эквивалентных БМФ; б) сокращаем на критический множитель;
а) воспользуемся таблицей эквивалентных БМФ; б) сокращаем на критический множитель; в) вычисляем предел
в) вычисляем предел

 а) приведением выражения под знаком предела к общему знаменателю;
а) приведением выражения под знаком предела к общему знаменателю;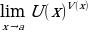 =
= 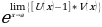 Волошина Н.Н.
Волошина Н.Н.









