Параллельность прямой и плоскости

ВАРИАНТ 1

З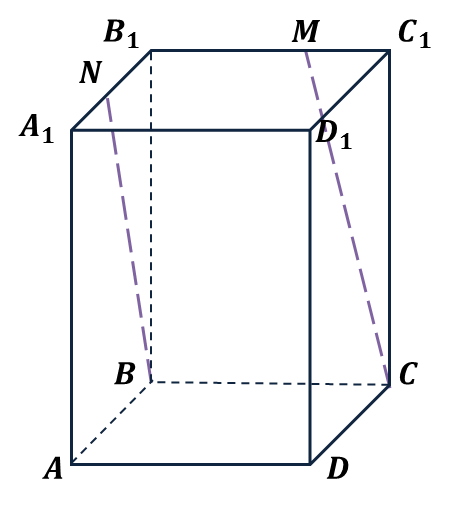 адание 1

Вопрос: Укажите верное утверждение. Прямая CМ:

В ыберите один из 4 вариантов ответа:

1) пересекает плоскость АВА₁

2) параллельна прямой ВN

3) пересекает плоскость АА₁D₁

4) параллельна плоскости АА₁В₁

Задание 2

Вопрос: Дано: АВ параллельно плоскости α, AD параллельно BC. Найти: угол ADC. (в ответе укажите только число, например, 90)

Запишите число: ___________________________

Задание 3

Вопрос: Если в пространстве даны две параллельные прямые, плоскость, в которой они не лежат, и одна из прямых параллельна плоскости, то параллельна ли плоскости другая прямая?

Выберите один из 3 вариантов ответа:

1) не всегда 2) нет 3) да

Задание 4

В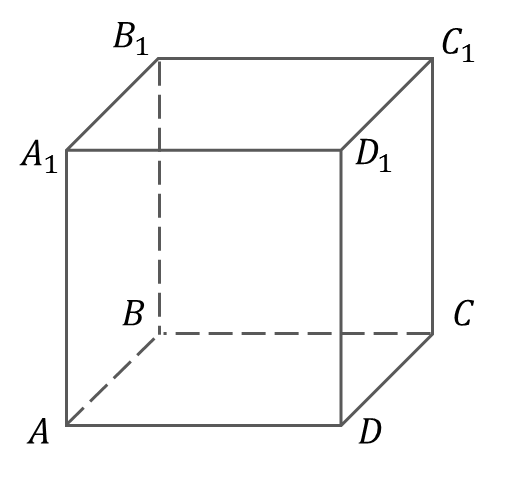 опрос: Если прямая не имеет с плоскостью общих точек, то как относительно плоскости расположена эта прямая?

Выберите один из 3 вариантов ответа:

1) параллельно 2) лежит в плоскости 3) пересекает

Задание 5

Вопрос: Сколько плоскостей, заданных вершинами куба, параллельны прямой CD? (в ответе укажите только число)

Запишите число: ___________________________

З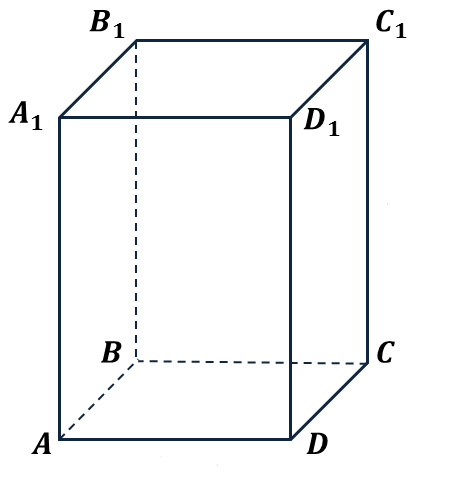 адание 7

Вопрос: Сколько прямых, заданных вершинами прямоугольного параллелепипеда, параллельны плоскости A₁DC? (в ответе укажите только число)

З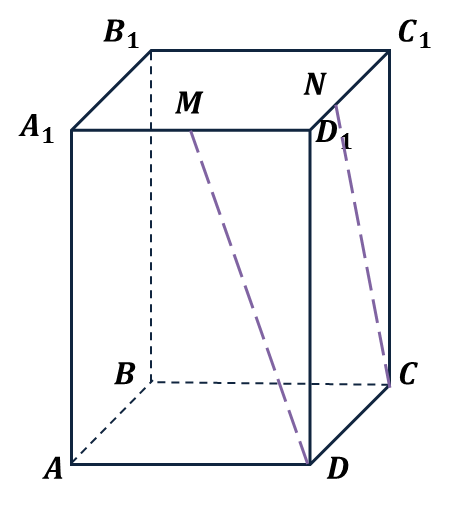 апишите число: ___________________________

Задание 8

Вопрос: Укажите верное утверждение. Прямая СN:

Выберите один из 4 вариантов ответа:

1) пересекает плоскость АА₁В

2) параллельна плоскости ADM

3) параллельна прямой DM

4) параллельна плоскости АА₁В₁

Задание 9

Вопрос: Сколько прямых, параллельных данной плоскости, можно провести в пространстве через точку, не принадлежащую этой плоскости? (в ответе укажите только число)

Выберите один из 5 вариантов ответа:1) 10 2) 2 3) 3 4) 1 5) бесконечно много

Задание 10

Вопрос: Сколько существует вариантов взаимного расположения прямой и плоскости в пространстве?

Выберите один из 3 вариантов ответа:

1) 2 2) 3 3) 1

Задание 11 Реши задачу

Дан треугольник ABC, F ϵ AB, N ϵ AC, AB : AF = AC : AN = 9 : 4. Через прямую BC

проходит плоскость β, не совпадающая с плоскостью треугольника ABC.

1) Докажите, что FN II β.

2) Найдите длину отрезка FN, если BC = 18 см.