Параллельность прямых и плоскостейв пространстве

Тема: Параллельность прямых, прямой и плоскости

b

а

d

с

а ll b

n

c ∩ d

m

m ― n

Две прямые называются параллельными , если они лежат в одной плоскости и не пересекаются.

а ll b



а

b

4

4

4

4

4

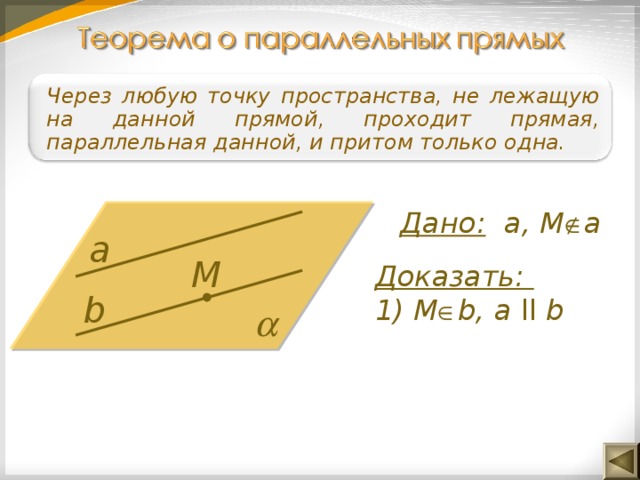
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Дано: а, М  а

а

М

Доказать:

1) М  b, a ll b

b



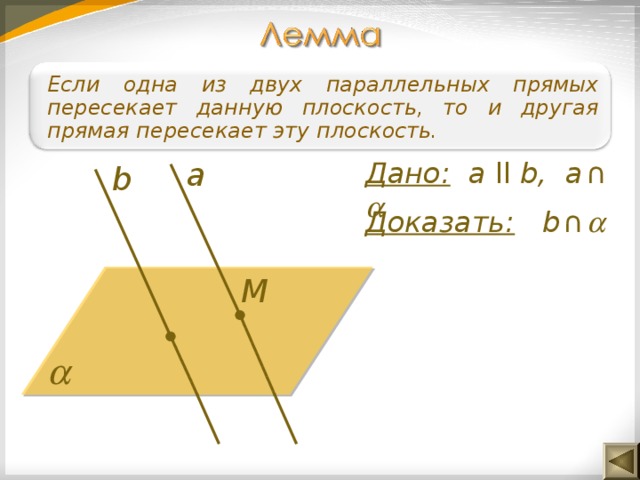
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

a

Дано: а ll b, a ∩ 

b

Доказать: b ∩ 

M



Если две прямые параллельны третьей прямой, то они параллельны.

c

Дано: а ll c; b ll c

К

b

Доказать: а ll b

( а   , b   , a ∩ b )

а



11

b

с



β

М

с ll 

b ∩ β



а

a  

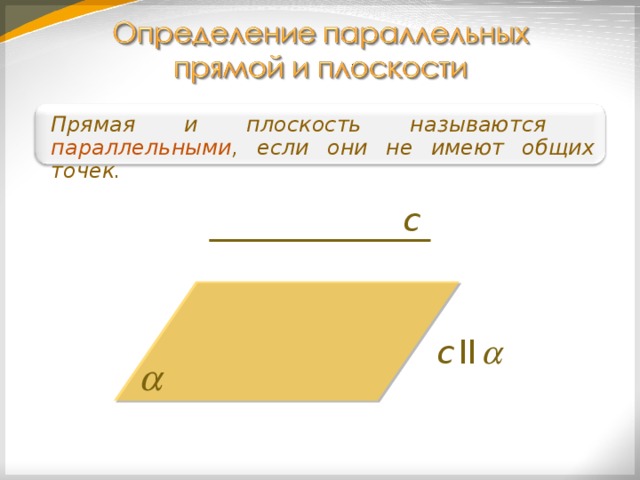
Прямая и плоскость называются параллельными , если они не имеют общих точек.

c

с ll 



13

13

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

a

Дано:

a   , b   , а ll b

b

Доказать: а ll 



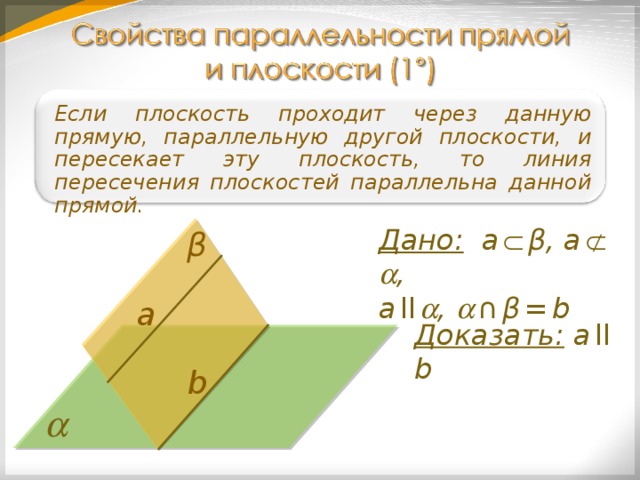
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Дано: a  β , a   ,

а ll  ,  ∩ β = b

β

а

Доказать: а ll b

b



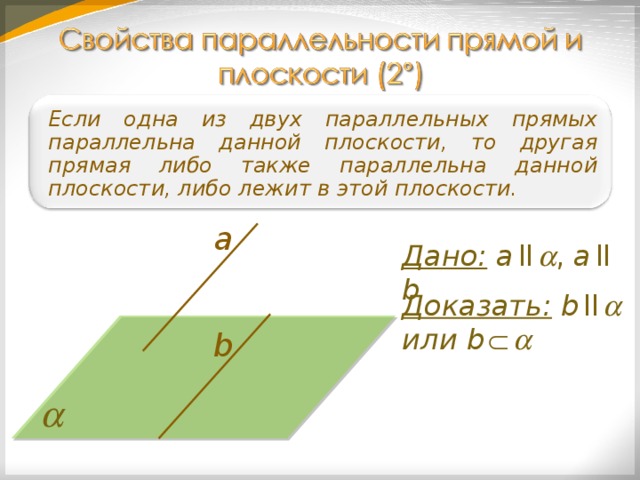
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

а

Дано: а ll  , а ll b

Доказать: b ll 

или b  

b



Дано: ∆ АВК; АВ ll  ; ( АВК ) ∩  = С D ; С K = 8; АВ = 7; АС = 6 Доказать: АВ ll С D Найти: С D

В

А

С

D



K

Дано: ∆ АВС; АВ ∩  = В 1 ; АС ∩  = С 1 ; ВС ll  ; АВ : ВВ 1 = 8 : 3 ; АС = 16 см Доказать: В C ll B 1 С 1 Найти: АС 1

А

В 1

С 1



В

С

• Тема: «Скрещивающиеся прямые».

21

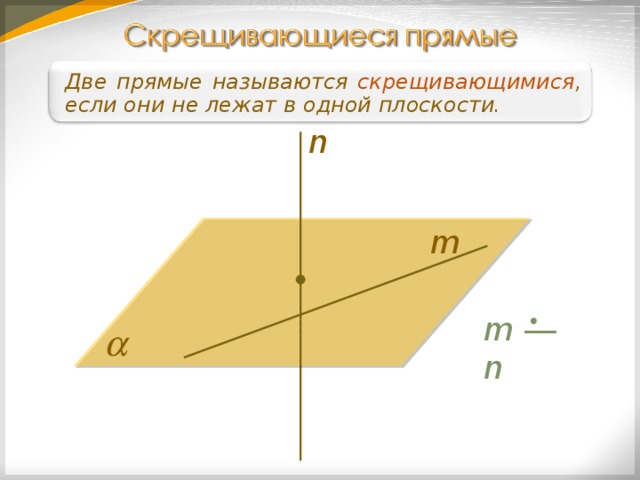
Две прямые называются скрещивающимися , если они не лежат в одной плоскости.

n

m

m ― n



23

23

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

D

В

С

А



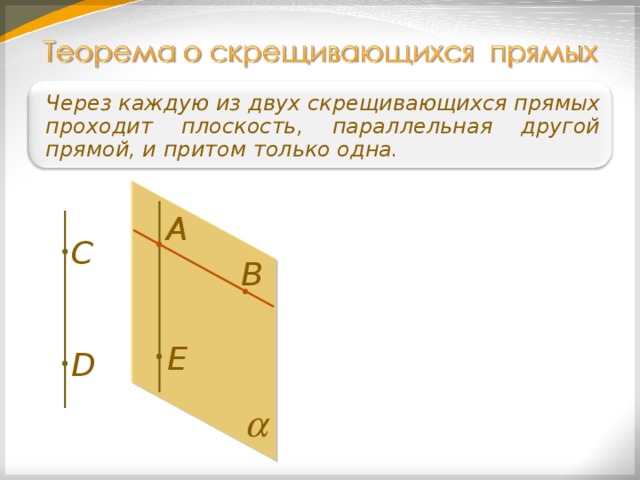
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

А

С

В

Е

D



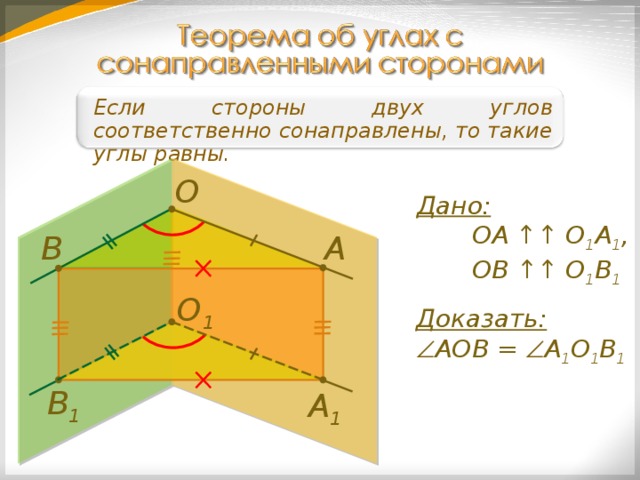
Если стороны двух углов соответственно сонаправлены, то такие углы равны.

О

Дано:

ОА ↑↑ О 1 А 1 ,

ОВ ↑↑ О 1 В 1

В

А

О 1

Доказать:

 АОВ =  А 1 О 1 В 1

В 1

А 1



180º-φ

φ

а

b

А

А 1

φ

С



D

В

В 1

β

В

С

А



D

β

В

N

М

А

С

Q

P



D

Дано: ABCD – параллелограмм,

Р  α,  РАВ = φ.

Найти:  ( АР; CD).

P 1

P

Вариант 1

Вариант 2

φ

φ

А

D

В

С



• Геометрия. 10 – 11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ]. – 19-е изд. – М.: Просвещение, 2010.
• Изучение геометрии в 10 – 11 классах: кн. для учителя / С.М. Саакян, В.Ф. Бутузов. – 4-е изд., дораб. – М.: Просвещение, 2010.

• https://www.goodfon.ru/download/rzhd-relsy-zheleznaya-doroga/1366x768/ - рельсы

• http://old.stroi.mos.ru/photogallery/photo/otkrytie-estakady-na-yaroslavskom-shosse-v-raione-ulicy-veshnih-vod-s-sobyanin-m-husnullin-bochkarev-19 - открытие эстакады на Ярославском шоссе
• http://www.cepolina.com/rs/bridge-highway-traffic-tunnel.htm - тоннели
• http://temptrans.ru/news/3514/ - Керченский мост
• http://www.votpusk.ru/country/dostoprim_info.asp?ID=9805 – Парфенон Греция
• http://fototelegraf.ru/265466-nedelya-v-fotografiyax.html/comment-page-1 - тоннель в Китае
• https://commons.wikimedia.org/wiki/File:Intersection_i10_i155_CA_USA.JPG?uselang=ru – дороги

28

28