
Тема урока:
«Перпендикулярные прямые в пространстве»
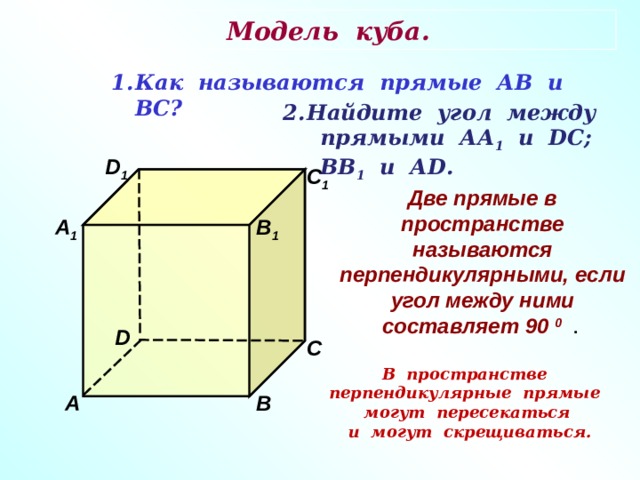
Модель куба.
- Как называются прямые АВ и ВС?
прямыми АА 1 и DC ;
ВВ 1 и А D .
D 1
С 1
Две прямые в пространстве называются перпендикулярными, если угол между ними составляет 90 0 .
В 1
А 1
D
С
В пространстве
перпендикулярные прямые
могут пересекаться
и могут скрещиваться.
А
В
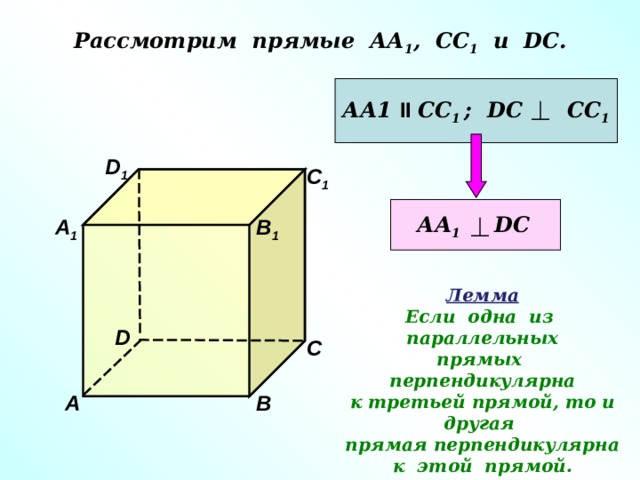
Рассмотрим прямые АА 1 , СС 1 и DC .
АА1 II СС 1 ; DC СС 1
D 1
С 1
АА 1 DC
В 1
А 1
Лемма
Если одна из параллельных
прямых перпендикулярна
к третьей прямой, то и другая
прямая перпендикулярна
к этой прямой.
D
С
А
В
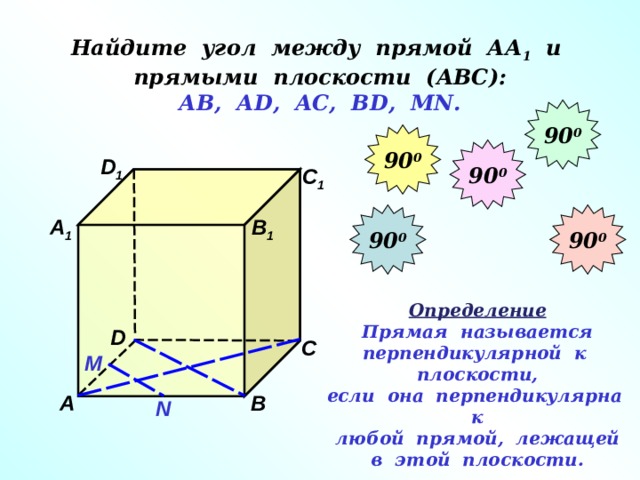
Найдите угол между прямой АА 1 и прямыми плоскости (АВС): АВ, А D , АС, В D , М N .
90 0
90 0
90 0
D 1
С 1
90 0
90 0
В 1
А 1
Определение
Прямая называется
перпендикулярной к плоскости,
если она перпендикулярна к
любой прямой, лежащей
в этой плоскости.
D
С
М
А
В
N

Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
a
a
5

Канат в спортивном зале перпендикулярен плоскости пола.
5

Подвес люстры обычно перпендикулярен плоскости потолка и плоскости пола. Но бывают моменты, когда эта ситуация меняется.
5

Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.
а 1
а
х
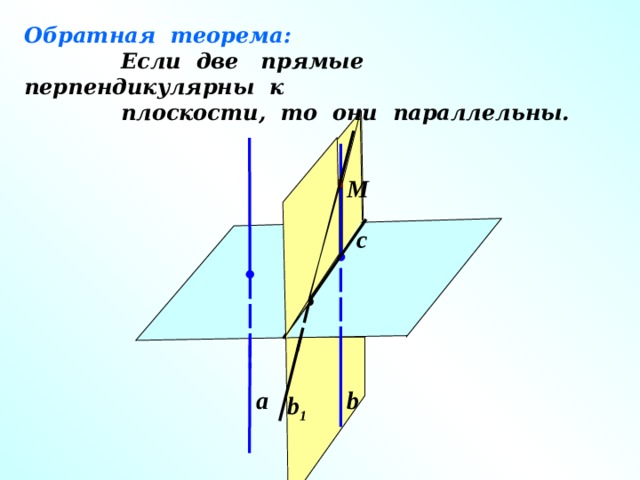
Обратная теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
M
c
b
а
b 1

№ 117.
В тетраэдре АВС D ВС А D . Докажите, что А D MN , где М и N – середины ребер АВ и АС.
D
II
N
А
C
M
B
10

№ 119. Прямая ОА OBC . Точка О является серединой отрезка А D . Докажите, что АВ = В D .
По опр.
A
O
В
Л.С. Атанасян №119.
С
D
11

№ 119. Прямая ОА OBC . Точка О является серединой отрезка А D , ОВ = ОС. Докажите, что АВ = АС.
По опр.
A
В
O
Л.С. Атанасян №119.
С
С
D
12

№ 119. Прямая ОА OBC . Точка О является серединой отрезка А D . ОВ = ОС. Докажите, что АВ = АС.
По опр.
A
В
O
Л.С. Атанасян №119.
С
С
D
13

№ 120. Через точку О пересечения диагоналей квадрата, сторона которого равна a , проведена прямая ОК, перпендикулярная к плоскости квадрата. Найдите расстояние от точки К до вершин квадрата, если ОК = b .
По опр.
К
b
В
С
Л.С. Атанасян №120.
a
O
А
a
D
14

№ 121. В треугольника АВС дано: С = 90 0 , АС = 6 см, ВС = 8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем
СК = 12 см. Найдите КМ.
По опр.
К
А
12 см
6см
М
Л.С. Атанасян №121.
С
8 см
В
15

№ 121. Еще один эскиз к задаче
К
12 см
С
6см
А
8 см
Л.С. Атанасян №121.
М
В
16

АВС – правильный треугольник. О – его центр, ОМ – перпендикуляр к плоскости АВС, ОМ = 1. Сторона треугольника равна 3. Найдите расстояние от точки М до вершин треугольника.
По опр.
М
1
В
А
Зив Б.Г. «Дидактические материалы по геометрии для 10 класса»
O
3
С
17

Через вершину А треугольника АВС проведена плоскость, параллельная ВС, ВВ 1 и СС 1 , СС 1 =4, АС 1 =
АВ 1 = , . Найдите ВС.
ВВ 1
СС 1
В
С
4
4
В 1
С 1
Л.С. Атанасян №125.
А
18

Дано:
Дано:
АВС –равносторонний треугольник со стороной
О – точка пересечения медиан. Найти расстояние от точки М до вершин треугольника.
АВС D – квадрат со стороной 4, О – точка пересечения диагоналей. Найти расстояние от точки М до вершин квадрата.
М
М
1
2
В
А
4
В
С
Зив Б.Г. «Дидактические материалы по геометрии для 10 класса» Самостоятельная работа
4
O
O
4
А
4
D
С
19

№ 124. Прямая Р Q параллельна плоскости . Через точки Р и Q проведены прямые, перпендикулярные к плоскости , которые пересекают эту плоскость соответственно в точках Р 1 и Q 1 . Докажите, что Р Q = P 1 Q 1 .
РР 1
QQ 1
Р
Q
PP 1 IIQQ 1
P 1
Q 1
Л.С. Атанасян №124.
20

ABCD – параллелограмм. BE (ABC), DF (ABC)
Доказать: (АВЕ) II (С DF)
ВЕ (АВС)
DF (АВС)
Е
ВЕ II DF
F
В
С
AB II DC
( AB Е) II ( CDF)
D
А
21

№ 125. Через точки Р и Q прямой PQ проведены прямые, перпендикулярные к плоскости , которые пересекают эту плоскость соответственно в точках Р 1 и Q 1 . Найдите Р 1 Q 1 .
Q
15
РР 1
QQ 1
Р
PP 1 IIQQ 1
33,5
21,5
P 1
Q 1
Л.С. Атанасян №125.
По опр.
22





































