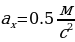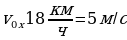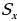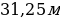| Нам необходимо вывести формулу, с помощью которой мы могли бы рассчитывать проекцию вектора перемещения тела, движущегося прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к рисунку 14 на стр 29 вашего учебника. Как на рисунке 14а, так и на рисунке 14б, отрезок АС представляет собой график проекции вектора скорости тела, движущегося с постоянным ускорением а. Вопрос к классу: по какой формуле при прямолинейном равномерном движении тела определяется вектор перемещения, совершенного над этим телом? (по той же формуле, что и площадь прямоугольника, заключенного под графиком проекции вектора скорости. Какой вывод мы можем сделать? ( проекция вектора перемещения численно равна площади этого прямоугольника). Докажем, что и в случае прямолинейного равноускоренного движения проекцию вектора перемещения можно определить по той же формуле, что и площадь фигуры, заключенной между графиком АС, осью Оt и отрезками ОА и ВС. Т.е. что и в этом случае проекция вектора перемещения численно равна площади фигуры под графиком скорости. Для этого на оси Ot (рис 14а) выделим маленький промежуток времени db. Из точек d и b проведем перпендикуляры к оси Ot до их пересечения с графиком проекции вектора скорости в точках a и c. Таким образом, за промежуток времени, соответствующий отрезку db, скорость тела меняется от 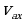 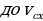 . . За достаточно малый промежуток времени проекция вектора скорости меняется очень незначительно, поэтому движение тела в течение этого промежутка времени мало отличается от равномерного, т.е. от движения с постоянной скоростью. В этом случае участок ас графика можно считать горизонтальной, а полоску acbd прямоугольником. Значит площадь этой полоски численно равна проекции вектора перемещения за промежуток времени, соответствующий отрезку db. На такие полоски можно разбить всю площадь фигуры OACB, которая какой является фигурой? Следовательно, чему будет равна проекция вектора перемещения за промежуток времени, соответствующий отрезку ОВ? (площади трапеции, и определяется по той же формуле что и эта площадь). Чему равна площадь трапеции? Из рисунка 14б найдем основания и высоты трапеции. Назовите их. АО=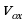 , ВС= , ВС=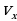 , ОВ=t , , ОВ=t , Следовательно, с учетом вышесказанного выведите формулу для нахождения площади трапеции. Следовательно: 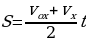 (1) (1) Вспомним, чему равна скорость при равномерном равноускоренном движении? 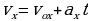 С учетом того, что S=Sx, формулу (1) можно переписать в ином виде. Каждый из учеников записывает получившуюся формулу в свою тетрадь. И проверяет ее с той, которую учитель выводит на доске. Т.о. мы получили формулу для расчета проекции вектора перемещения при равноускоренном движении. 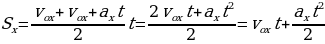 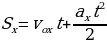
По этой же формуле рассчитывают проекцию вектора перемещения и при движении тела с уменьшающейся по модулю скоростью, только в этом случае векторы скорости будут направлены в противоположные стороны и их проекции будут иметь разные знаки. Показ видеофрагмента «Демонстрация равноускоренного прямолинейного движения». Вопросы к учащимся по демонстрации. | 





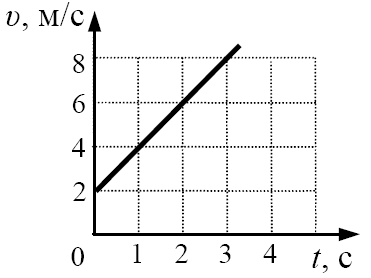
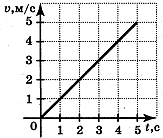 По графику скорости, изображенному на рисунке, определите путь, пройденный телом за 5 с.
По графику скорости, изображенному на рисунке, определите путь, пройденный телом за 5 с.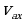
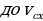 .
. 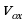 , ВС=
, ВС=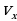 , ОВ=t ,
, ОВ=t ,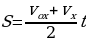 (1)
(1)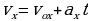
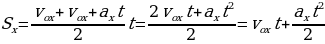
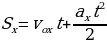
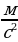 . Определить длину горки, если известно, что в начале скорость велосипедиста была равна 18 км/ч.
. Определить длину горки, если известно, что в начале скорость велосипедиста была равна 18 км/ч.