План-конспект урока по алгебре для 8 класса по теме «Квадратные уравнения» Эпиграф к уроку:
«Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным».
Паскаль
Цели урока:
Образовательные:
Сформировать у учащихся практические навыки решения квадратных уравнений с помощью применения формул корней квадратных уравнений. Показать уровень усвоения программного материала по теме «Квадратные уравнения»,
Развивающие:
Способствовать расширению кругозора учащихся, развитию приемов умственной деятельности, логического мышления, памяти, внимания, умения сопоставлять, анализировать, делать выводы, а также
развитию познавательной активности, формированию навыков самоконтроля, мотивации к учению, потребности к самообразованию.
Воспитательные:
Способствовать формированию чувства ответственности, взаимопонимания, взаимоподдержки, уверенности в себе;
Ход урока: 1. Организационный момент «Настроимся на урок!»
Здравствуйте, ребята и гости нашего урока! Математику не зря называют «царицей наук», ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики — любознательность. Постараемся доказать это сегодня на уроке.
Чтобы узнать тему нашего занятия, послушаем следующие строки: Их необходимо решать, как первой степени, так и второй-это …
(Уравнения), а именно , речь пойдет сегодня об уравнениях второй степени.
Знания, ребята, не только надо иметь, но и надо уметь их показать, что вы и сделаете сегодня на уроке, а я вам в этом помогу.
Цель урока:
Закрепить навыки решения квадратных уравнений с помощью применения формул корней квадратных уравнений,
Эпиграфом к уроку я взяла слова великого математика Паскаля «Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным». В течение урока мы еще вернемся к этим словам.
2. Проверка домашнего задания
Начнем урок с проверки домашнего задания.
Правильность решения заданий вы не сможете проверить, т. к. на предыдущем уроке каждый получил индивидуальное задание в зависимости от способностей и возможностей, поэтому я попрошу вас сдать один комплект тетрадей.
А вот знание теоретического материала, который понадобится нам на протяжении всего урока, давайте вспомним.
- Какой вид имеет квадратное уравнение?
- Какие виды квадратных уравнений вы знаете? (полные и неполные)
- Сколько решений имеет полное квадратное уравнение? От чего это зависит?
3. Тест «Квадратные уравнения»
Итак, мы повторили, как можно решить квадратное уравнение, а сейчас я хотела бы проверить, как вы усвоили эти формулы и определения.
Ученики имеют сопроводительные листы с заданиями. Заполняют пропущенные слова в карточках.
I вариант
Уравнение вида ax2 + bx + c = 0, где a, b, c — заданные числа, x — переменная, называется квадратным.
Полное квадратное уравнение не имеет корней, если D меньше 0.
Уравнение вида x2 +bx = 0 называется неполным квадратным уравнением, где с равно 0, а =1.
Квадратное уравнение имеет два корня, если b2 - 4ac больше 0.
Дано уравнение 3x2 - 7x + 4 = 0. D =1.
2 вариант
Как называется квадратное уравнение, у которого старший коэффициент а = 1?
Уравнение вида аx2 + с = 0 называется неполным квадратным уравнением, где b=0.
Полное квадратное уравнение имеет единственный корень , если D= 0.
Уравнение вида ax2 + bx + c = 0, где а,b,c не равны 0,называется полным квадратным уравнением.
Дано уравнение x2 - 6x + 8 = 0. D =4.
Проводится взаимопроверка, учащиеся обмениваются карточками. Ответы показываем на мультимедиа.
4. Работа в парах:
Вернемся к эпиграфу нашего урока. Попытаемся сделать математику сегодня на уроке более занимательной.
Вам необходимо угадать, зашифрованное слово.
Даю три определения этому предмету:
Непроизводная основа слова.
Число, которое после подстановки его в уравнение обращает это уравнение в тождество.
Один из основных органов растений. /Корень/
Учитель: Вы должны определить, какого растения это корень, решив следующие уравнения:
x2 - 8x + 15 = 0
x2 - 11x + 18 = 0
x2 - 5x - 6 = 0
x2 - 4x + 4 = 0
3x2 + 4x + 20 = 0
5x2 - 3x - 2 = 0
Найдите полученный ответ на экране. Если ученики получают правильный ответ, то получат изображение розы.
Учитель: Что это за растение?
Ответ: Роза.
Ученик: В народе говорят: «Цветы ангельские, а когти дьявольские». О розе существует интересная легенда: по словам Анакреона, родилась роза из белоснежной пены, покрывающей тело Афродиты, когда богиня любви выходила из моря. Поначалу роза была белой, но от капельки крови богини, уколовшейся о шип, стала алой.
Учитель: Видите, ребята, все в этом мире взаимосвязано: математика, русский язык, литература, биология. Мы увидели, что слово «корень» встречается не только на уроках математики.
Физкультминутка: поднять глаза на тренажер.
Использование квадратных уравнений для решения задач по геометрии и физике.
Давайте узнаем, с какими еще предметами связано решение квадратных уравнений? Для этого решим следующие задачи и получим ответ на данный вопрос.
Задача1: Одна сторона прямоугольника на 5 м больше другой. Площадь его равна 36 м2 вычислите стороны прямоугольника.
Учитель: Каким способом будем решать задачу?
Ученики: Алгебраическим.
Учитель: Какую величину примем за неизвестное?
Ученики: Длину одной из сторон. Обозначим ее буквой х.
Учитель: чему равна длина другой стороны?
Ученики: х + 5
Учитель: чему равна площадь прямоугольника?
Ученики: произведение его длины на ширину.
Учитель: Какое уравнение можно составить по условию задачи?
Ученики: х(х+5)=36.
Ученики решают это уравнение в тетрадях самостоятельно, один из учеников комментирует решение вслух с места. х2+5х-36=0. х1= -9, х2=4. Число -9 не удовлетворяет условию задачи, так как х- длина отрезка, а она не может быть числом отрицательным. Ответ: b=4м, а=9м.
Этот пример показывает, что квадратные уравнения широко применяются при решении геометрических задач.
Задача 2: Определите, сколько времени будет падать камень, брошенный, вертикально с крыши дома с высоты 12 м?
Учитель: из курса физики вам известна формула 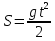 . Назовите величины входящие в нее.
. Назовите величины входящие в нее.
Ученики: S – расстояние, которое преодолевает тело(камень), t – время движения(падения) и g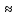 10м/с2 –ускорение свободного падения.
10м/с2 –ускорение свободного падения.
Учитель: какое уравнение получится после подстановки в формулу известных величин?
Ученики: 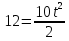 или 5
или 5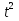 = 12.
= 12.
Задача свелась к решению неполного квадратного уравнения. Время падения камня t=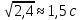 .
.
Ответ: 1,5с.
Этот пример из практики показывает применение квадратных уравнений в физике.
6. Рефлексия:
Вариант 1:
7x2 + 3x -4 = 0
Вариант 2:
4x2 + 7x + 3 = 0
Заполните таблицу, распределив уравнения по видам.
| Уравнение | Полное | Неполное | Приведенное |
| 7х2 +9х+2=0 | + | | |
| 6x2+x=0 | | + | |
| x2 –1=0 | | + | |
| y2 –3у–4=0 | | | + |
| (2x-1)²=0 | + |
|
|
7. Итог урока: Выставление отметок, шкала на доске.
8. Домашнее задание: на доске
И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
















