Тема: Образование, чтение, запись чисел и их сравнение: число, цифра, натуральное число, нуль, ряд натуральных чисел,
Цель урока: Повторение, обобщение и систематизация знаний об образовании, чтении, записи чисел и их сравнении.
Задачи: повторить знания о натуральных числах, приёмах их сравнения, работать над понятием натуральный ряд, или ряд натуральных чисел.
Ход урока.
Организационный момент.
Прозвенел и смолк звонок,
Начинаем мы урок.
Мы за парты дружно сели
Друг на друга посмотрели
Пожелай успех глазами
И вперед, вперед за знаниями!
Проверка домашнего задания.
Актуализация опорных знаний.
1. Фронтальная работа.
- Дан ряд чисел: 1, 115, 229, 343.
-Какое число лишнее? (1). Почему?
-Назовите самое маленькое число и самое большое в этом ряду.
- В каком порядке расположены числа?
-Расскажите, что вы знаете о числе 1? (Наименьшее натуральное, однозначное, предыдущее 0, последующее 2).
- С какого числа начинается натуральный ряд чисел?
-Назовите наибольшее натуральное число. (Невозможно).
- Все последующие числа больше или меньше предыдущих?
- Найдите закономерность и назовите последующие числа. (Больше на 114. 457, 571,685).
- Расскажите все о числе 343. (Натуральное, трёхзначное, содержит 3сотни, 4 десятка и 3 единицы, предыдущее - 342, последующее - 344, сумма цифр - 10).
2. Работа в парах. Сравнить числа.
На карточках:
78 945 * 78 946 67 090 * 67 190
125 891 * 125 881 259 051 * 250 051
2 991 224 * 2 990 224 23 460 748 * 23 460 748
Фронтальная проверка.
3. Постановка темы и цели урока.
Повторение.
1. Чтение с пометами. Работа по учебнику с.273.
- Назовите натуральные числа.
- Для чего используют натуральные числа?
- Является ли нуль натуральным числом?
- Какие числа образуют натуральный ряд?
- Назовите первое натуральное число.
- Есть ли последнее натуральное число?
2. Дополнительные сведения о числах. Можно заранее раздать детям.
Числа начинают получать имена.
Перекладывать камушки и глиняные фигурки с места на место было довольно утомительным занятием. Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать имена для чисел.
О том, как появились имена у чисел, ученые узнают, изучая языки различных племен и народов. Например, оказалось, что у нивхов, живущих на Сахалине, числительные зависят от того, какие предметы считают. Важную роль играет форма предмета, так что по-нивхски в сочетаниях «два яйца», «два камня», «два глаза» и т. д. числительные различны. Одному и тому же русскому слову «два» у них соответствует несколько десятков различных слов. Нечто подобное было и у древних людей.
И должно было пройти много столетий, а может быть, и тысячелетий, прежде чем одни и те же числительные стали применять к предметам любого вида. Вот тогда и появились общие названия для чисел. Сначала названия получили только числа 1 и 2. Название для числа «один» связывалось обычно со словом «солнце», а название для числа «два» — с предметами, встречающимися попарно: крыльями, ушами и т. д. Но бывало, что числам 1 и 2 давали иные имена. Иногда их связывали с местоимениями «я» и ты». А были языки, где «один» звучало так же, как «мужчина», а «два» — «как «женщина».
У некоторых племен еще совсем недавно не было других числительных, кроме «один» и «два». А все, что шло после двух, называлось «много». Но потом понадобилось называть и другие числа. Ведь и собак у охотника, и стрел у него, и овец у пастуха может быть больше, чем две. И тут придумали замечательный выход: числа стали называть, повторяя несколько раз названия для единиц и двоек.
Например, на языке некоторых папуасских племен, живущих на острове Новая Гвинея в Тихом океане, и сейчас числительное «один» звучит «урапун», «два» — «окоза», а число 3 они называют «окоза-урапун», число 4 «окоза-окоза». Так они дошли до числа 6, которое получило имя «окоза-окоза-окоза». А дальше у них идет уже знакомое нам название «много» (конечно, по-папуасски). И 10 у них «много», и 100 тоже «много».
Позднее другие племена дали особое имя числительному, которое мы называем «три». А так как до того они считали «один», «много», то это новое числительное стали применять вместо чисел «много». И сейчас мать, рассердившись на сына, говорит ему: «Что, я три раза должна повторять одно и то же!» Русская пословица говорит: «Обещанного три года ждут». А в сказках злой царь посылает героя искать Кощея Бессмертного «за тридевять земель», в тридесятое царство».
Иногда числом 3 обозначали окружающий человека мир. Наземное, подземное и небесное царства. Поэтому число 3 стало у многих народов священным. Когда они придумали легенды о богах, выделяли из них трех самых главных.
В русских сказках число З также играло особую роль. Во многих из них участвуют три брата, герой сражается с трехглавым змеем, проходит три царства — медное, серебряное и золотое. Число 4 встречается в сказках куда реже. Но о том, что и оно на каком-то этапе развития играло особую роль, видно из русской грамматики. Мы говорим: «одна лошадь», две лошади», три лошади», «четыре лошади». Казалось бы, все хорошо: после единственного числа идет множественное. Но, начиная с пяти, мы говорим: пять лошадей», шесть лошадей», и будь их хоть миллион, а все равно — «лошадей». Значит, когда-то за числом 4 и в русском языке начиналась необозримая область «много».
На более поздних этапах в роли слова «много» выступало число 7. Об этом говорят различные пословицы и поговорки:
«Семеро одного не ждут», «Семь раз отмерь — один раз отрежь», «Один с сошкой, семеро с ложкой», «Семь бед один ответ», «Лук от семи недуг» и т. д. Так постепенно люди осваивали счет.
Первые названия чисел некоторые племена стали применять 20 тысяч лет тому назад. А вот слово для обозначения числа 1000 возникло лишь 5—7 тысяч лет назад.
Долгое время после того, как появились названия чисел, люди их не записывали. Причина для этого была самая уважительная — они не умели писать. Поэтому, если кому-нибудь надо было переслать другому человеку сведения, где участвовали числа, прибегали к зарубкам на дереве или на кости, к узелкам не веревках, рисункам на мягкой глине и т. д. Такие знаки уже нельзя было перекладывать с места на место, убирать одни и добавлять другие. Вместо этого приходилось думать, мысленно выполнять операции над знаками.
Но все же это еще не была настоящая арифметика. Знаки на глине обозначали не числа, а предметы — головы скота, мешки с зерном, кувшины масла. Их приходилось изображать столько же, сколько было предметов. С этим еще можно было мириться, пока учет велся в пределах одного хозяйства, одной деревни. Но когда возникли государства, старые методы обозначения чисел были негодными. Для записи большие числа уже нельзя было обозначать ни зарубками на бирках, ни узелками, ни глиняными фигурками.
Примерно 5 тысяч лет тому назад было сделано знаменитое открытие. Люди догадались, что знаком цифры можно обозначать не только голову скота, а сразу 10 или 100 голов, не один мешок зерна, а 6 или 60 мешков.
Немало различных способов записи чисел было создано людьми. В древней Руси числа обозначали буквами с особым знаком (титло), который писали над буквой. Первые 9 букв — десятки, а последние 9 букв — сотни. Число 10 тысяч называли словом тьма».
Интересны были различные методы обозначения чисел, придуманные египтянами и вавилонянами, греками и римлянами. Но у этих методов был один недостаток: по мере увеличения чисел придумывали все новые и новые знаки. Один из величайших древнегреческих математиков Архимед научился называть громадные числа, но обозначать их он не умел. Не хватало ему самой малости. Архимед, один из гениальнейших математиков в истории человечества, не додумался до... нуля!
Знакомясь в первом классе с числом 0, мог ли кто-нибудь себе представить, что это одно из величайших изобретений в математике. Только после того, как люди научились обозначать пропущенные разряды в позиционной записи чисел, они получили в руки могучее орудие познания природы. Без нуля не было бы современной математики, не было бы и таких достижений человеческого разума, как вычислительные машины и космические корабли.
Впервые нуль был придуман вавилонянами примерно две тысячи лет тому назад. Но они применяли его лишь для обозначения пропущенных разрядов в середине числа. Писать нули в конце записи числа они не догадались.
В Индии примерно полторы тысячи лет тому назад нуль был присоединен к девяти цифрам, и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было. И самое главное, запись таких гигантских чисел стала довольно короткой. Если бы живший 30 тысячелетий тому назад древний человек имел представление о миллионе и захотел бы изобразить это число с помощью зарубок на волчьих костях, ему пришлось бы истребить 20 тысяч волков. А для записи миллиарда не хватило бы волков во всех европейских лесах. Теперь же вся запись умещается в одной строке! Приведем название некоторых больших чисел с указанием числа нулей после единицы.
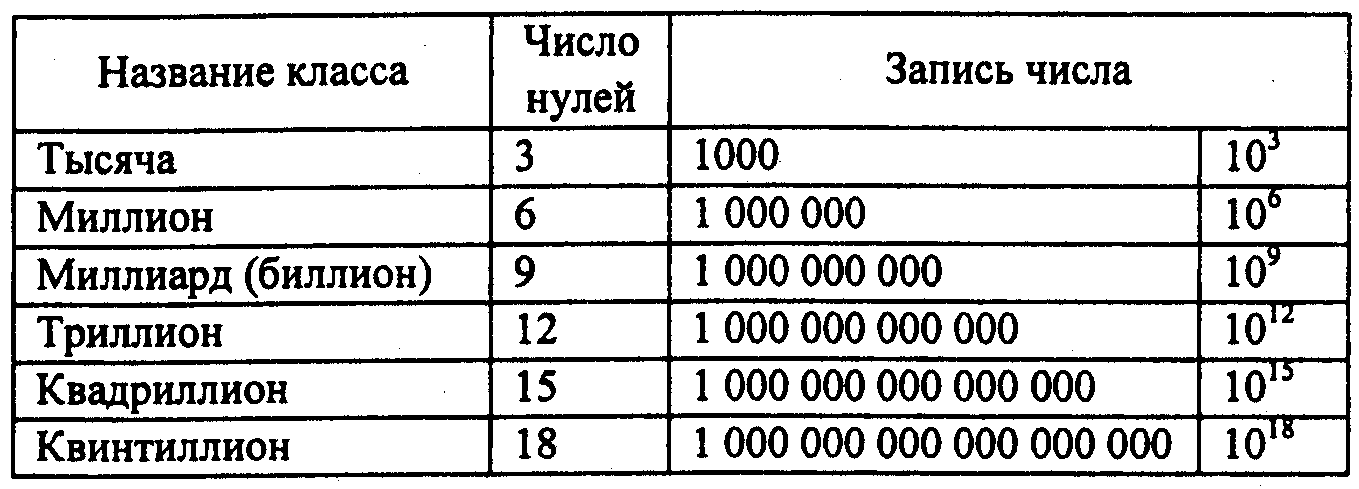
Индийской системой обозначений мы пользуемся до сих пор. Это не значит, что индийские цифры имели с самого начала современный вид. В течение многих столетий, переходя от народа к народу, они много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры и позиционную десятичную систему записи чисел. Европейцы в свою очередь узнали ее от арабов. Поэтому наши цифры, в отличие от римских, стали называться арабскими. Правильнее было бы называть их индийскими. Они употребляются в нашей стране начиная примерно с ХVII века
3. Самостоятельная работа. № 2 с.273. Каждый выберет то задание, с каким он справится.
4. Коллективная работа с классом.
Решение задачи с.274 № 5. Один человек у доски.
- Что известно в задаче? За 5 дней завод должен выпускать 920 швейных машин. Рабочие стали выпускать на 16 машин в день больше.
- Что нужно узнать? Сколько швейных машин выпустит завод за 255 рабочих дней?
- Что нам нужно знать, чтобы ответить на вопрос задачи? Сколько выпускают швейных машин в один день.
-Как это узнать? Надо 920 разделить на 5 = 184. Это при старой производительности.
- Что произошло с увеличением производительности труда? Стали в день производить на 16 машин больше.
-Значит, сколько машин производят в день при повышенной производительности труда? 184 + 16 = 200 машин.
- Как узнать, сколько машин выпустит завод за 255 дней, если в один день производит 200 швейных машин? Надо 200 умножить на 255 = 5100 машин.
| V | К | А |
| ? машин | 5 дней | 920 машин |
| ?, на 16 машин | 255 дней | ? машин |
1). 920 : 5 = 184 (машин) – в день при старой производительности труда.
2). 184 + 16 = 200 (машин) – в день при новой производительности труда.
3). 200 ∙ 255 = 5100 (машин) – за 255 дней.
Ответ: 5100 машин выпустит завод за 255 рабочих дней.
5. Физминутка.
Раз – подняться, потянуться,
Два – согнуться, разогнуться,
Три – в ладоши три хлопка, головою три кивка,
На четыре – руки шире,
Пять – руками помахать,
Шесть - за парту тихо сесть.
6. Самостоятельная работа.
Нахождение значений числовых выражений №7 с.274.
1 ряд: 800000 - (1724 + 3012 ∙ 24) = 725 988
2 ряд: 5709 + (2100 – 46550 : 98) = 7334
3 ряд: 586 ∙ 908 – 31212 : 306 = 531 986
Фронтальная проверка.
7. Коллективная работа.
Выполнение задания повышенной сложности с.274 № 9.
различных комплектов одежды можно составить из трёх юбок и четырёх блузок.
V. Подведение итогов урока.
- Какую тему мы сегодня повторяли?
- Что вы можете сказать о натуральном ряде чисел?
- Назовите наименьшее натуральное число.
- Что вам удалось?
- Что на ваш взгляд было трудно?
VI. Домашнее задание: № 3, № 6 с.273, 274.
Вариативная часть.
Решение логического задания.
Найди последнее число.
А) 6 10 18 34… ?
Б) 0 3 8 15…?
В) 1 8 16 25…?
Ответы:
А) 66 (каждое число равно удвоенному предыдущему минус 2)
Б) 24 (к каждому числу прибавляли нечётные числа: 3,5,7,9)
В) 35 (к каждому предыдущему числу надо прибавить соответственно 7,8,9,10, чтобы получилось следующее число).

















