План-конспект открытого урока по математике
Преподаватель: Смаилова Эльзара Рефатовна
Аудитория: группа 113
Дисциплина: математика
Тема урока: «Замена переменных при решении тригонометрических уравнений».
Цели урока:
Образовательная: повторить, обобщить и систематизировать знания по теме «Решение тригонометрических уравнений», проверить практические навыки и умения студентов при решении уравнений, научить применять знания, умения и навыки в новой ситуации.
Развивающая: развивать логическое мышление, вычислительные навыки, умение пользоваться справочными материалами, таблицами, расширить кругозор студентов, развивать любознательность, самостоятельность мышления.
Воспитывающая: воспитывать стремление к овладению знаниями, интерес к предмету, потребность в самостоятельном приобретении знаний, культуру мышления, культуру речи, воспитывать чувство ответственности, уверенности в себе.
Задачи урока: использовать и применять формулы при решении практических задач в рамках изучаемой темы.
Оборудование: интерактивное оборудование, раздаточный материал, тетради, учебные принадлежности.
Тип урока: урок повторения, обобщения и систематизации знаний по теме.
Вид урока: урок-практикум.
Ход урока:
Организационный момент.
Приветствие, проверка готовности к уроку, проверка присутствующих. Организация рабочего места студентов.(1 мин.)
Организация и мотивация образовательной деятельности.
Французский математик и физик Паскаль говорил: “Предмет математики настолько серьезен, что полезно не упускать случаев делать его намного занимательным”.
Я решила начать последовать совету Паскаля и предложить вам разгадать такой ребус.
Решение ребуса. (Ответ: тригонометрия)
Как вы думаете, почему я предложила вам расшифровать такое слово? Что оно означает?
“Тригонометрия” происходит от греческого слова τριγουο треугольник и греческого μετρειν измерять, т.е. означает измерение треугольников. Тригонометрия - это раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.
Одной из наиболее важных тем тригонометрии является решение тригонометрических уравнений, с которыми мы познакомились в этом учебном году. Эта тема очень актуальна и важна, т.к. широко представлена на ЕГЭ, возможно, кто-то из вас решит поступать дальше и ему пригодятся эти знания.
Тема сегодняшнего урока “Замена переменных при решении тригонометрических уравнений”. Открыли тетради, записали число и тему урока. Сообщение цели урока.
Восточная мудрость гласит: “Приобретать знания - храбрость, приумножать их - мудрость, а умело применять - великое искусство”
Какие-то знания по теме “Тригонометрические уравнения” мы уже приобрели, приумножать знания - никогда не поздно, поэтому и на сегодняшнем уроке будем мудрыми, и еще раз посмотрим, насколько умело вы применяете свои знания.(5 мин.)
Актуализация знаний в форме фронтального опроса.
Что необходимо знать, чтобы решить любое тригонометрическое уравнение? (Ответ: общие формулы решения простейших тригонометрических уравнений.)
Какие простейшие тригонометрические уравнения вы знаете?
(Ответ: sin x = a, cos x = a, tg x = a, ctg x = a.)
Давайте вспомним общие формулы их решений.
Простейшие тригонометрические уравнения sin x = a, cos x = a. (Ответ: 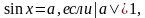 то корней нет, а если
то корней нет, а если 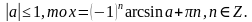
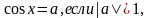 то корней нет, а если
то корней нет, а если 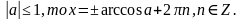 )
)
Что надо помнить при решении таких уравнений? (Ответ: частные случаи.)
Уравнения вида tg x = a и ctg x = a.(Ответ: 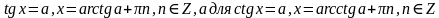 ) (5 мин.)
) (5 мин.)
Проверим, насколько хорошо вы решаете простейшие тригонометрические уравнения.
Итак, у вас на партах перед каждым лежат задания по вариантам. Ваша задача указать общую формулу, по которой находятся все корни уравнения.
Записали в своих тетрадях номер варианта, далее записываем номер задания и ответ.(2 мин.)
Выполнение задания по вариантам.
Проверьте себя! (Указаны правильные ответы).
Углубление знаний по теме.
Как правило, решение тригонометрических уравнений сводится к решению простейших уравнений с помощью преобразований тригонометрических выражений, разложения на множители и замены переменных.
Следует помнить общий ориентир, когда замена переменных может выполняться без преобразования данных тригонометрических выражений.
Если в уравнение, неравенство или тождество переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить одной буквой (новой переменной). (Записать в тетрадь) (3 мин.)
Итак, на слайде представлен алгоритм решения тригонометрических уравнений, которые сводятся к простейшим методом замены:
Ввести замену
Решить уравнение после замены
Вернуться к замене
Проверить корни
Решить простейшее тригонометрическое уравнение (Алгоритм записать в тетрадь)
Теперь, я предлагаю вам разобрать, как осуществляется алгоритм решения уравнений.
Задача 1: Решите уравнение 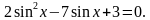
Решение: Пусть 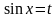 , тогда получаем
, тогда получаем
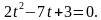
Отсюда 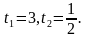
При 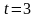 имеем
имеем 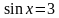 – уравнение не имеет корней, т.к.
– уравнение не имеет корней, т.к.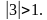
При 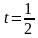 имеем
имеем 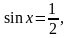 тогда
тогда
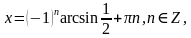
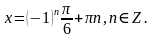
Ответ: 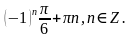
Задача 2: Решите уравнение 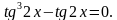
Что вам не понятно? Ну что же, приступим к применению ваших знаний.
Закрепление материала.
Решение задачи у доски.
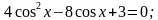
А сейчас, давайте посмотрим, насколько вы освоили тему урока. У каждого из вас на парте листочек с уравнением. Сверху подписали фамилию, имя, номер группы. Решение выполняем прямо на листочках. Полностью решенное уравнение с правильным ответом оценивается в «5»; записана замена, полученное уравнение, решено не до конца – оценка «4»; записана замена и полученное уравнение – оценка «3»; ничего не решено – оценка «2».
Вариант 1) 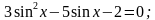
Вариант 2) 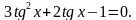
Давайте осуществим взаимопроверку. Сейчас проверяем I вариант. Оценку выставляем по алгоритму, за каждый правильный шаг по 1 баллу. Проверяем II вариант. Посчитайте баллы и выставьте оценки. Верните друг другу листочки. Поднимите руки, кто получил «5» - …, «4» - …, «3» - … А, кто ничего не сделал?
Выдача домашнего задания:
Решить уравнения:
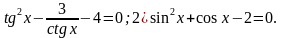
(Вспомнить: 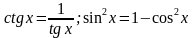 )
)
Подведение итогов.
Итак, давайте подведем итог нашего урока. Вернемся к восточной мудрости, знания по теме «Тригонометрические уравнения» мы уже приобрели, на сегодняшнем уроке мы эти знания приумножили, и умело применяли.
Рефлексия.
Я думаю, что вы получили такое же удовольствие от урока, как и я.
Всем спасибо за урок. Листочки сдайте, пожалуйста, чтобы я могла выставить оценки в журнал.







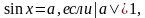 то корней нет, а если
то корней нет, а если 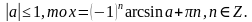
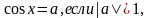 то корней нет, а если
то корней нет, а если 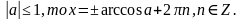 )
)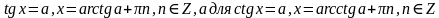 ) (5 мин.)
) (5 мин.)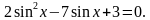
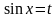 , тогда получаем
, тогда получаем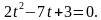
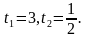
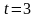 имеем
имеем 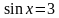 – уравнение не имеет корней, т.к.
– уравнение не имеет корней, т.к.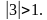
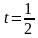 имеем
имеем 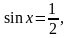 тогда
тогда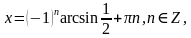
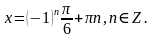
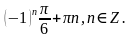
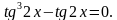
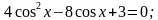
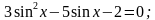
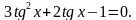
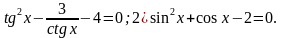
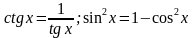 )
)









