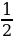План-конспект занятия по теме: "Тригонометрические функции острого угла"

Раздел 6. «Основы тригонометрии»

Тема 6.1 : «Тригонометрические функции острого угла»

Тригонометрия возникла как аппарат для вычисления неизвестных параметров треугольника по заданным значениям других его параметров. Так, методами тригонометрии по данным сторонам треугольника можно вычислить его углы, по известной площади и двум углам вычислить стороны и т.д. Необходимость отыскивать неизвестные параметры данного треугольника впервые возникла в астрономии, и в течение долгого времени тригонометрия была одним из ее разделов.

Первые методы нахождения неизвестных параметров данного треугольника были развиты учеными Древней Греции за несколько веков до нашей эры. Греческие астрономы не рассматривали синусов, косинусов и тангенсов. Вместо таблиц этих величин они составили и использовали таблицы, позволяющие отыскивать хорду окружности по стягиваемой ею дуге. Дальнейшее развитие тригонометрия получила в средние века в работах индийских и арабских ученых. Современные буквенные обозначения появились в тригонометрии в середине XVIII века. Приблизительно в то же время в тригонометрии стала рассматриваться радианная мера угла, были введены тригонометрические и обратные тригонометрические функции числового аргумента, после чего тригонометрия приобрела свой современный вид.

Тригономе́трия (от др.-греч. «треугольник» и «измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595.

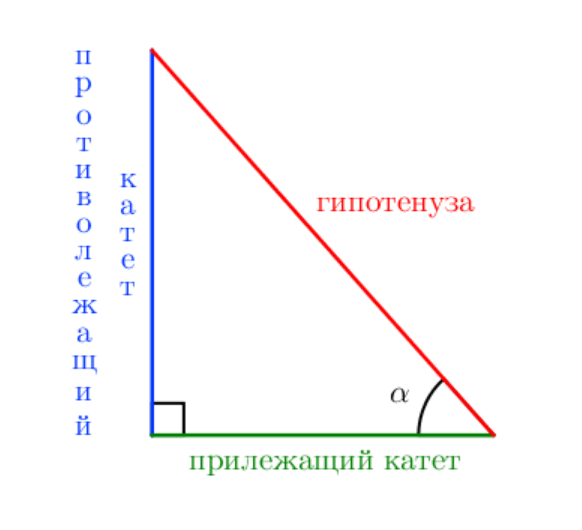
Основные понятия:

Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

Пример 1.

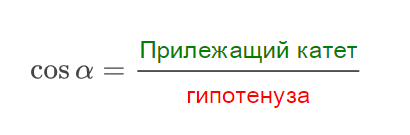
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Пример 2.

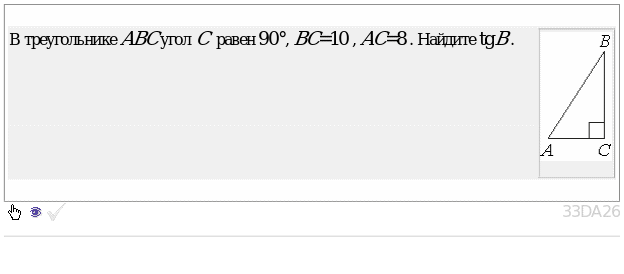
Т ангенсом острого угла в прямоугольном треугольнике называется отношение противоположного катета к прилежащему катету.

Пример 3.

К отангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противоположному катету.

П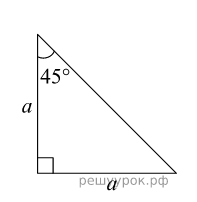 ример 4.

Найдите значения котангенса отмеченного угла по данным рисунка.

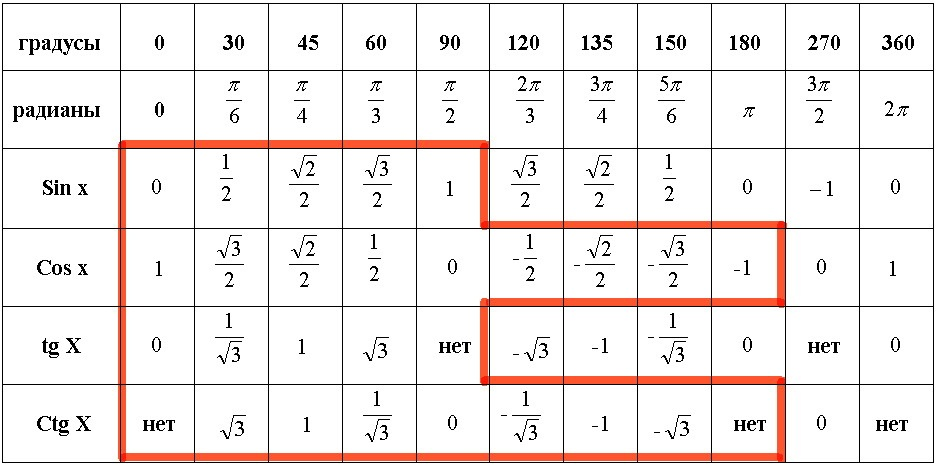
Вычислить:

1. Н а клетчатой бумаге с размером клетки 1 х 1  изображён угол. Найдите sin AOB, cos AOB, tgAOB, ctgAOB:

1. Н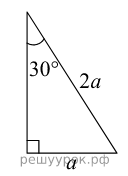 айите значение sin, cos, tg, ctg угла 30 ⁰

3)

a) sin30 º-√2cos45º

b) cos90º-√27tg30º

c) √2cos135 ⁰ +log₂8 - 9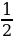

d) 3ctg 2 120⁰ -cos60⁰ sin150⁰

e) tg30⁰ ctg60⁰ sin45⁰ cos45⁰

f) sin45⁰ cos45 -log₂₅ 5+ 3⁴

Домашнее задание:

Учить конспект, готовится к устному опросу.

2