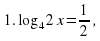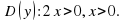МБОУ Низовская СОШ
Методическая разработка по математике
План-конспект занятия
«Логарифмические уравнения, системы уравнений и методы их решения»
Составила: Семёновых И.Н.– учитель математики.
2012-13 уч. год.
План-конспект занятия.
Тема: Логарифмические уравнения, системы уравнений и методы их решения.
Учебно-воспитательные задачи.
Дидактическая цель. Сформировать умения и навыки решения несложных логарифмических уравнений, систем уравнений.
Воспитательная цель. Развивать продуктивное мышление и навыки самоконтроля в процессе выполнения упражнений. Систематически обращать внимание н грамотность записей, на умение пользоваться математической символикой в процессе решения упражнений, усилить внимание к развитию творческого мышления и повышения интереса к предмету.
Основные знания и умения.
Знать: определение логарифмического уравнения; основные методы и приемы решения логарифмических уравнений и систем.
Уметь: решать несложные логарифмические уравнения и системы.
Обеспечение занятия.
Раздаточный материал. Карточки-задания для проверочной работы.
Т.С.О. интерактивная доска.
Методические рекомендации.
Вид занятия. Формулирование умений и навыков.
Мотивация познавательной деятельности. Для активации познавательной деятельности необходимо создавать проблемные ситуации при отыскании методов решения логарифмических уравнений и систем в процессе их решения.
Последовательность изложения нового материала.
Определение логарифмического уравнения.
Способы решения логарифмических уравнений, систем.
Решение логарифмических уравнений и систем логарифмических уравнений.
План занятия.
Проверка домашнего задания.
Провести проверочную работу. Примерное содержание одного варианта:
1. Решить уравнения:
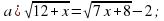
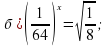
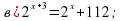
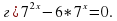
2. Решить неравенства:
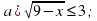
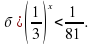
Ответ:
1. а) 4; б) 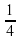 ; в) 4; г) 0;
; в) 4; г) 0; 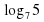 .
.
2. а) 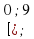 б) (4; ∞).
б) (4; ∞).
Повторение опорных знаний.
Повторить с учащимися определение и свойства логарифмической функции, формулы логарифмирования (потенцирования), формулы перехода от одного основания логарифма к другому, понятия и теоремы о равносильности уравнений.
Изучение нового материала.
Теоретическая часть
(весь материал идет с показом на интерактивной доске).
Определение: Логарифмическим уравнением называется уравнение, содержащее неизвестное только под знаком логарифма.
Общего метода решения логарифмических уравнений, как и показательных, не существует.
Логарифмические уравнения, как и показательные, рассматриваются только в множестве действительных чисел. Проверка найденных значений неизвестного по условию уравнения в общем случае является обязательной.
Уравнение вида
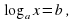
где х – неизвестное, а «а» и «b» - заданные числа, называется простейшим.
Если а 0 и а 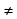 1, то такое уравнение при любом действительном значении «b» имеет единственное решение
1, то такое уравнение при любом действительном значении «b» имеет единственное решение
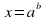
2. Логарифмическое уравнение
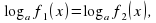
где 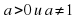 , после потенцирования приводится к виду
, после потенцирования приводится к виду
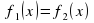
Корнями уравнения 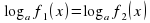 будут только те корни уравнения
будут только те корни уравнения
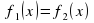 , при которых
, при которых 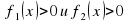 , т.е. корни, принадлежащие к области определения уравнения
, т.е. корни, принадлежащие к области определения уравнения 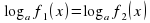 .
.
3. Логарифмические уравнения вида
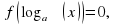
где 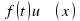 - некоторые заданные функции, заменой
- некоторые заданные функции, заменой 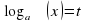 приводятся к уравнению
приводятся к уравнению 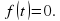
II. Применение знаний при решении типовых примеров и задач.
Решить примеры типа:
а) базовый уровень (тренировочный тест с решением)
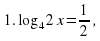
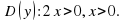
По определению


Ответ: x=1.


Ответ: x = 2.


Ответ: x = -0,25.










 + +
+ +
-2 -  x
x




Ответ: x = 2.




Ответ: x = -113.


Ответ: x =  .
.
Решим это уравнение на уровне равносильных преобразований
Геометрически:














-1 0 x










 + +
+ +
-1 -  x
x



-1 1 x
Ответ: x = 1.
Геометрически:









3 x



1 4 x

Ответ: x = 4.
б) повышенный уровень
10. Решите уравнение
Примем во внимание, что

 .
.
Пусть  . Тогда
. Тогда


Ответ:  .
.
11. Решите систему уравнений:
т.к.  Следовательно,
Следовательно,  т.е. система не имеет решения.
т.е. система не имеет решения.
* 
Следовательно, наша система равносильна совокупности:
Ответ: (2;  ).
).
Тренировочные упражнения.
Базовый уровень.
Решите уравнения:



Решите системы логарифмических уравнений:
Повышенный уровень:
Ответы:
1. x=4;
2. x=11;
3. x=15;
4. x=216;
5.  ;
;
6. 
7. x=4;
8. x=64;
9. x=16;
10. x=27;
11. (1; 10);
12. (2; 6);
13. (16; 25), (25; 16);
14. (6; 8), (8; 6);
15. (16; 4).
Подведение итогов занятия.
Домашнее задание:
1. Повторить основные определения, формулировки и формулы изучаемой темы.
2. Тренировочные упражнения №1-15.
Анализ усвоения материала:
Тренировочные упражнения №1-11 выполнило около 80% учащихся.
Тренировочные упражнения № 12-15 – около 5% учащихся.
Основные трудности при разборе решения заданий №12-15 в самом начале: в выборе пути решения (с чего начать?): какие необходимо выполнить преобразования, состоящие в замене какого-то фрагмента данного соотношения другим фрагментом на основании конкретной формулы или свойства, справедливые при имеющихся в данном соотношении ограничениях.
Поэтому учащимся должны быть предложены следующие рекомендации:
Одно ли основание во всех логарифмах?
Приведи все логарифмы к одному основанию. Лучше приводить к простому постоянному основанию.
Встречается ли в уравнении логарифм в степени, под корнем, в знаменателе дроби или произведение логарифмов?
Если есть хотя бы одно из указанных обстоятельств, раздроби входящие в уравнение логарифмы на возможно мелкие составляющие с тем, чтобы увидеть замену и перейти к уравнению без логарифмов.
Старайся собрать всё в один логарифм и прийти к соотношению простейшего вида.
Например, для уравнения вида:
Тема вызвала достаточный интерес учащихся.
Литература:
1. Сергиенко Л.Ю., Самойленко П.Н. «Планирование учебного процесса по математике» - М.: Высшая школа, 2007 г.
2. Н.В. Богомолов «Математика задачи с решениями» - М.: Дрофа, 2010 г.
3. К.И. Мазур «Решебник всех конкурсных задач по математике» под редакцией М.И. Сканави – Украинская энциклопедия 1995 г. – т. 2.
4. А.Х. Шахмейстер «Уравнения» - Спб.: «ЧеРо-на Неве», 2003 г.
5. Материалы курса «Уравнения и неравенства в школьном курсе математики»: Лекции 1-8. – М.: Пед. Университет «Первое сентября», 2010 г.
6. «Алгебра и начала анализа» 10-11 кл. А.Н. Колмагоров – М.: ВАКО, 2004 г.
7. Журнал (методический) «Математика» №9 октябрь 2012 г.





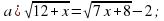
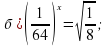
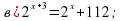
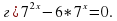
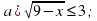
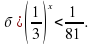
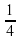 ; в) 4; г) 0;
; в) 4; г) 0; 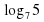 .
.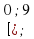 б) (4; ∞).
б) (4; ∞).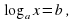
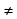 1, то такое уравнение при любом действительном значении «b» имеет единственное решение
1, то такое уравнение при любом действительном значении «b» имеет единственное решение 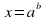
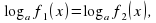
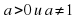 , после потенцирования приводится к виду
, после потенцирования приводится к виду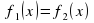
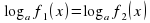 будут только те корни уравнения
будут только те корни уравнения 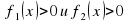 , т.е. корни, принадлежащие к области определения уравнения
, т.е. корни, принадлежащие к области определения уравнения 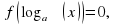
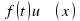 - некоторые заданные функции, заменой
- некоторые заданные функции, заменой 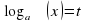 приводятся к уравнению
приводятся к уравнению