Функция у = k/x и ее график - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ
Цель: 1) закрепить и проверить полученные ранее навыки по теме преобразования рациональных дробей.
2) рассмотреть функцию у = k/x, ее свойства и график.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала.
a/b : с/d =a/b * d/c, 6x:1/2=(6x)/1*2/1=12x , a/b*c/d = ab/cd, 8/15*( 3y)/2= (8*3y)/( 15*2)=4y/5
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (Самост. работа дид.материалы Жохов). ( 20 мин)
Вариант 1. стр.13-15 Вариант 2. стр.57-58
1. С-9 №1.1)г,д; 2) а,г ; 2.1)а 1. С-9 №1.1)г,д; 2) а,г ; 2.1)а
2. С-10 №1)а,г 2. С-10 №1)а,г
3. С-11 1)а ; 3. С-11 1)а ;
4. На отд. оценку 4. На отд. оценку
С-11 4) С-11 4)
III. Изучение нового материала (основные понятия)
Пример 1
Пусть поезд, двигаясь со скоростью х км/ч за y часов, проехал расстояние 700 км. Тогда выполняется равенство ху = 700. Выразим из этого равенства переменную y = 700/x. При увеличении значения х в несколько раз соответствующее значение у уменьшается во столько же раз (т. е. чем быстрее движется поезд, тем меньше ему требуется времени для прохождения этого пути). Например, при скорости х = 35 км/ч время движения y = 700/35 = 20 часов. При скорости х = 70 км/ч (вдвое большей) время движения у = 700/70 = 10 часов (вдвое меньше). Видно, что время движения у обратно пропорционально скорости движения.
В этом примере переменные х и у принимали только положительные значения. В дальнейшем будут рассматриваться функции, задаваемые формулой вида у = k/x (где k — число, не равное нулю), в которой переменные х и у могут принимать и положительные и отрицательные значения.
К подобным функциям приводят многие задачи математики:
площадь S прямоугольника со сторонами а и b равна S = ab (откуда b = S/a),
и физики:
c) пройденный путь S при движении тела со скоростью V в течение времени t равен S = Vt (откуда t = S/V),
d) падение напряжения U на участке цепи с сопротивлением R при протекании тока I равно U = RI (откуда I = U/R) и т. д.
Обратной пропорциональностью называется функция вида у = k/x, где х — независимая переменная; k — число, не равное нулю.
(Определение в учебнике стр. 41)
Областью определения функции у = k/x является множество всех чисел, кроме нуля. Это следует из того, что выражение k/x имеет смысл при всех х ≠ 0.
Пример 2
Построим график функции у = 6/x, предварительно вычислив значения функции на промежутке -6 ≤ х ≤ 6.
| x | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
|
| -1 | -0,5 |
| y | -1 | -2 | -3 | -6 | 6 | 3 | 2 | 1 |
|
| -6 | -12 |
Отметим на координатной плоскости точки, координаты которых размещены в таблице (отмечены не все точки). Через эти точки проведен график данной функции.
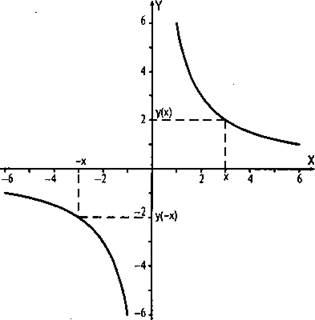
Выясним некоторые особенности графика функции.
Так как при х = 0 функция не определена, то на графике нет точки с абсциссой О (т. е. график не пересекает ось у). Для функции
у = 6/x при любых значениях х значение у не равно нулю. Область определения функции — множество всех чисел не равных нулю. Поэтому график не пересекает ось х.
Положительным значениям х соответствуют положительные значения у (первая координатная четверть). Отрицательным значениям х соответствуют отрицательные значения у (третья координатная четверть). (x0, y0 и xy
Из таблицы видно, что для противоположных значений х значения у также противоположны, т. е. у(-х) = -у(х). Функции, обладающие таким свойством, называются нечетными.
Очевидно, что точки с координатами (х, у) и (-х, -у) симметричны относительно начала координат. Так как равенство выполнено для любых допустимых значений х, то ветви графика симметричны относительно начала координат.
Рассмотрим ветвь графика, расположенную в первой координатной четверти. При уменьшении х знаменатель в выражении у = 6/x уменьшается. Поэтому значения у возрастают. Например, если х = 1, то у = 6; при х = 0,1 у = 60. При этом график функции приближается к оси ординат.
Прямая с уравнением х = 0 называется вертикальной асимптотой графика функции у = 6/x.
С увеличением х знаменатель в выражении у = 6/x возрастает. Поэтому значения y уменьшаются. Например, при х = 1 у = 6, при х = 10 у = 0,6, при х = 100 y = 0,06. Видно, что при достаточно больших значениях х значения функции y почти равны нулю. При этом график функции приближается к оси абсцисс. Прямая с уравнением у = 0 называется горизонтальной асимптотой графика функции у = 6/x.
Заметим, что такой же вид имеет график любой функции при любом значении k 0.
Пример 3 ( см. в тетради)
Построим график функции у = -6/x. Аналогично предыдущему примеру составим таблицу значений функции в промежутке -6 ≤ х ≤ 6. Отметим полученные точки на координатной плоскости и построим график функции.

Видно, что в этом случае график функции имеет те же особенности, что и в предыдущем примере. Область определения функции — множество всех чисел не равных нулю. График не пересекает осей координат.
График имеет вертикальную асимптоту с уравнением х = 0 и горизонтальную асимптоту с уравнением y = 0. График зависимости у = -6/x по-прежнему представляет собой кривую, состоящую из двух ветвей. Эти ветви симметричны относительно начала координат. Однако в отличие от графика функции у = 6/x в этом случае одна ветвь расположена во второй четверти, а другая ветвь — в четвертой координатной четверти.
График функции у = k/x при любом значении k имеет такой же вид, что и график, изображенный на рисунке. Ветви графика расположены во второй и четвертой четвертях.
Кривую, являющуюся графиком обратной пропорциональности у = k/x, называют гиперболой. Гипербола состоит из двух ветвей, симметричных относительно начала координат.
Пример 4
Гипербола проходит через точку A (2; -5). Напишем уравнение этой гиперболы.
Гипербола является графиком обратной пропорциональности у = k/x. Так как этот график проходит через точку А, то ее координаты удовлетворяют уравнению такой зависимости. Получаем: -5 = k/2. Из этого уравнения найдем k = -5 · 2 = -10. Следовательно, данная гипербола описывается зависимостью y = -10/х.
IV. Контрольные вопросы
1. Какая функция называется обратной пропорциональностью?
2. Основные особенности функции.
3. Нарисуйте эскиз графика функции для случая: а) k 0, б) k
4. Какая кривая называется гиперболой? Как располагаются ветви гиперболы?
V. Задание на уроке: 179, 181а) 184а) 194 а)
VI. Задание на дом: 180, 181 б); 184 б) ; 194б); 169а) ; 164а)
VII. Подведение итогов урока


















