ГИА. Справочные материалы по планиметрии

Планиметрия. Справочные материалы

Подготовка учащихся 9 классов к ГИА

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Треугольники

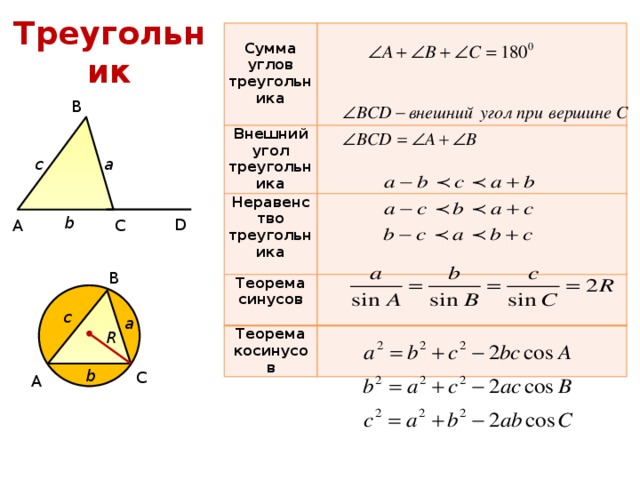
Сумма углов треугольника

Внешний угол треугольника

Неравенство треугольника

Теорема синусов

Теорема косинусов

Треугольник

В

а

c

b

D

С

А

В

c

а

R

b

С

А

Треугольник

В

Определение вида угла треугольника

Средняя линия треугольника

Площадь треугольника

а

c

А

С

b

В

N

М

С

А

c

h c

а

h a

h b

b

Треугольник и окружность

В

Около всякого треугольника можно описать окружность. Центр описанной окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

В прямоугольном треугольнике точка О – середина гипотенузы и радиус равен медиане, проведенной к гипотенузе

c

а

R

b

С

А

Во всякий треугольник можно вписать окружность. Центр вписанной окружности – точка пересечения биссектрис треугольника.

r

Виды треугольников

Равносторонний

Равнобедренный

В

В

a

а

а

a

b

С

С

А

a

А

H

Прямоугольный треугольник

С

А

М

В

С

А

В

Н

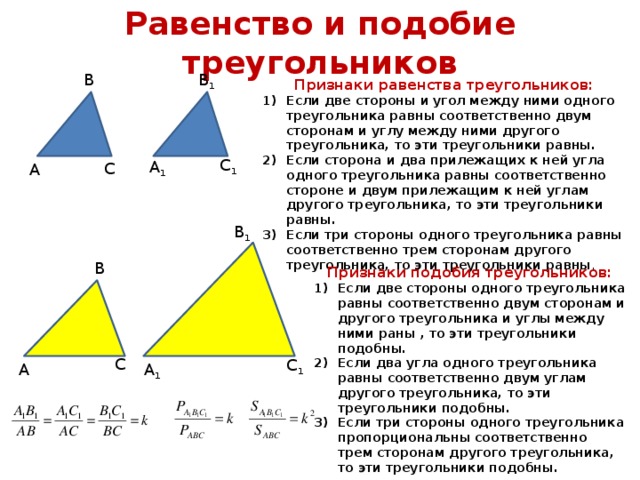
Равенство и подобие треугольников

В 1

В

Признаки равенства треугольников:

• Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
• Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.
• Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то эти треугольники равны .

С 1

А 1

С

А

В 1

В

Признаки подобия треугольников:

• Если две стороны одного треугольника равны соответственно двум сторонам и другого треугольника и углы между ними раны , то эти треугольники подобны.
• Если два угла одного треугольника равны соответственно двум углам другого треугольника, то эти треугольники подобны.
• Если три стороны одного треугольника пропорциональны соответственно трем сторонам другого треугольника, то эти треугольники подобны.

С

С 1

А 1

А

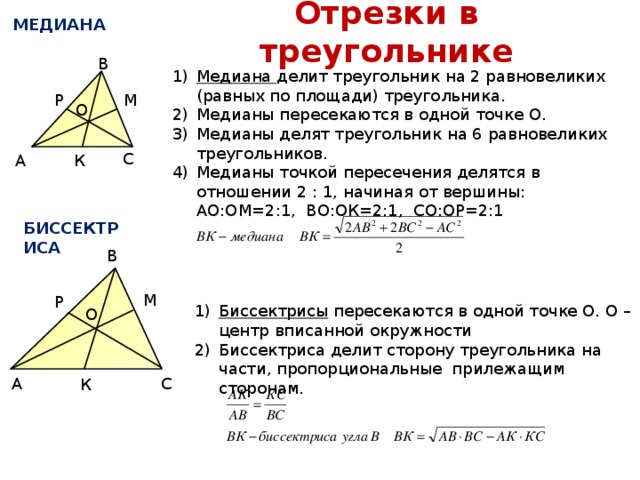
Отрезки в треугольнике

МЕДИАНА

В

• Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
• Медианы пересекаются в одной точке О.
• Медианы делят треугольник на 6 равновеликих треугольников.
• Медианы точкой пересечения делятся в отношении 2 : 1, начиная от вершины: АО:ОМ=2:1, ВО:ОК=2:1, СО:ОР=2:1

В

М

Р

О

Р

С

А

К

БИССЕКТРИСА

В

М

Р

• Биссектрисы пересекаются в одной точке О. О – центр вписанной окружности
• Биссектриса делит сторону треугольника на части, пропорциональные прилежащим сторонам.

О

С

А

К

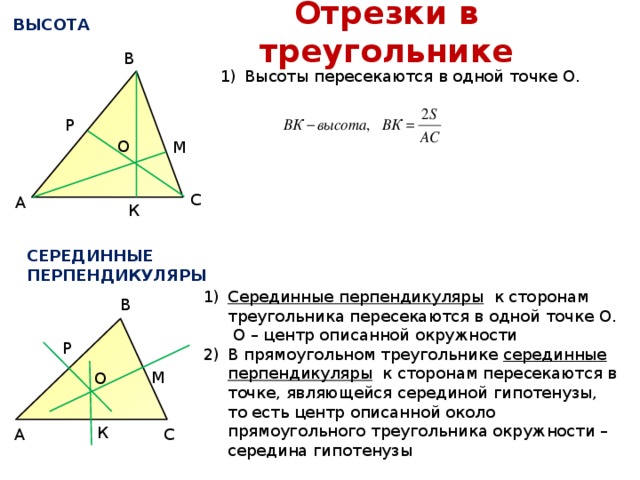
Отрезки в треугольнике

ВЫСОТА

В

• Высоты пересекаются в одной точке О.

Р

О

М

С

А

К

СЕРЕДИННЫЕ ПЕРПЕНДИКУЛЯРЫ

• Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке О. О – центр описанной окружности
• В прямоугольном треугольнике серединные перпендикуляры к сторонам пересекаются в точке, являющейся серединой гипотенузы, то есть центр описанной около прямоугольного треугольника окружности – середина гипотенузы

В

Р

М

О

К

К

С

А

Четырехугольники

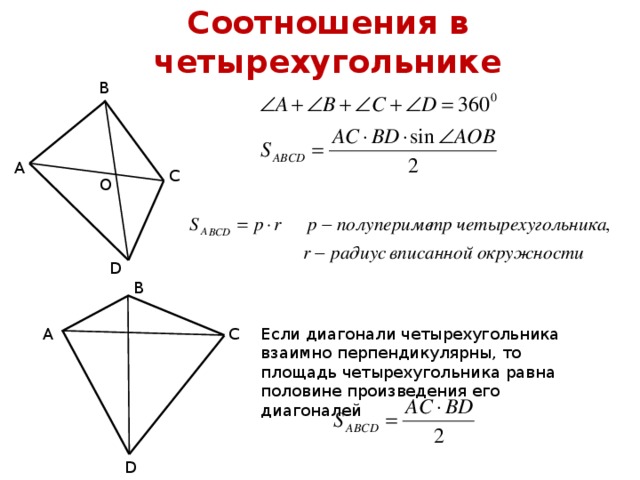
Соотношения в четырехугольнике

В

А

С

O

D

В

Если диагонали четырехугольника взаимно перпендикулярны, то площадь четырехугольника равна половине произведения его диагоналей

А

С

D

Четырехугольники и окружности

В

В

С

С

А

А

D

D

В четырехугольник можно вписать окружность, если:

Около четырехугольника можно описать окружность, если:

Задача. В четырёхугольнике АВСD АВ = 6, ВС = 9, СD = 14. Найдите АD, если известно, что в четырёхугольник АВСD можно вписать окружность.

Задача. Четырёхугольник АВСD вписан в окружность. Известно, что угол В равен 83° , угол А меньше угла D на 20 0 . Найдите угол С .

В

С

А

D

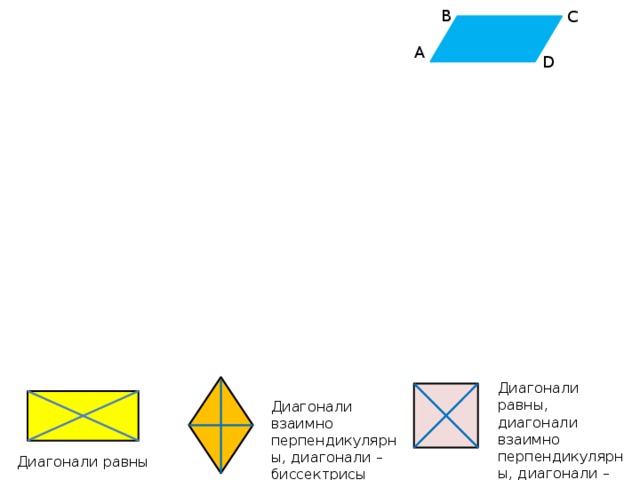
Диагонали равны, диагонали взаимно перпендикулярны, диагонали – биссектрисы углов

Диагонали взаимно перпендикулярны, диагонали – биссектрисы углов

Диагонали равны

Длины и площади в параллелограммах

С

В

С

В

О

Рис.2

Н

А

D

Рис.1

D

А

B

В

С

В

С

O

C

A

А

D

H

D

А

D

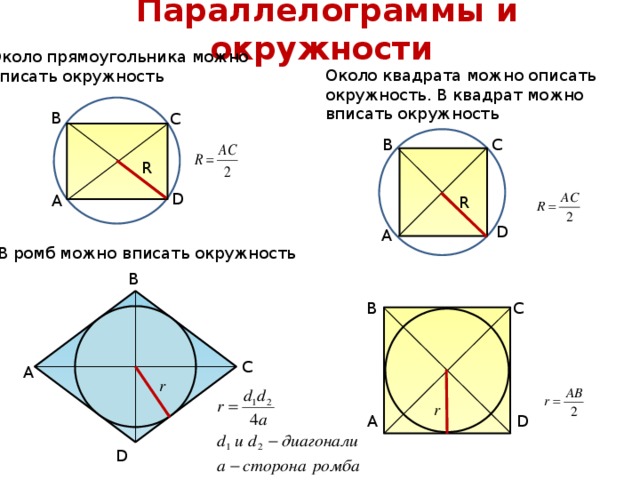
Параллелограммы и окружности

Около прямоугольника можно

описать окружность

Около квадрата можно описать окружность. В квадрат можно вписать окружность

B

C

C

B

R

D

A

R

D

A

В ромб можно вписать окружность

B

C

B

r

r

C

A

r

r

D

A

D

D

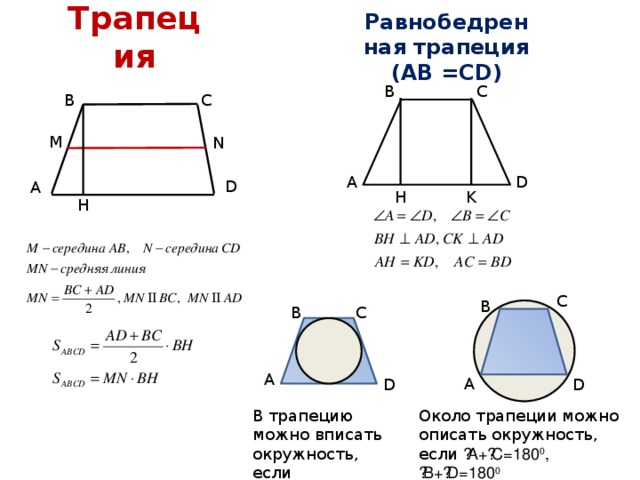
Трапеция

Равнобедренная трапеция (АВ =СD)

C

B

С

В

FA

M

N

A

D

D

А

K

H

H

C

B

В

С

А

A

D

D

В трапецию можно вписать окружность, если АВ+СD=АD+ВС

Около трапеции можно описать окружность, если ے А+ ے С=180 0 , ے B+ ے D=180 0

Длина окружности и площадь круга

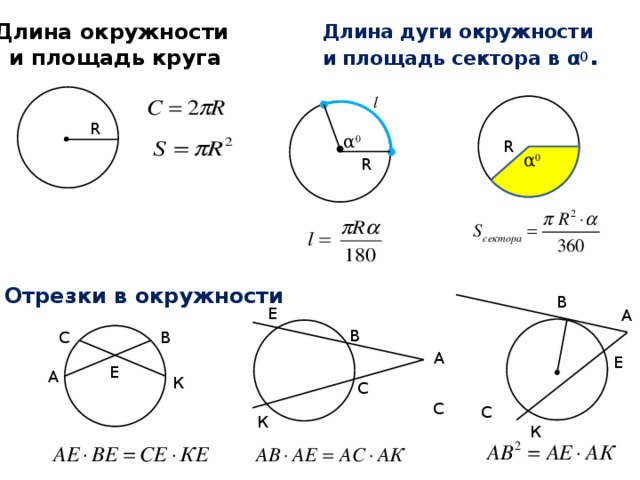
Длина окружности

и площадь круга

Длина дуги окружности и площадь сектора в α 0 .

l

R

α 0

R

α 0

R

Отрезки в окружности

В

Е

А

В

С

В

А

Е

Е

А

К

С

С

С

К

К

Площадь сегмента

Хорда разбивает круг на две части, каждая из которых называется сегментом

α

Площадь меньшего сегмента (белого)

Площадь большего сегмента (желтого)

Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны

Сумма углов выпуклого многоугольника равна 180 0 (n - 2)

Сумма внешних углов любого многоугольника равна 360 0 .

Правильный многоугольник и окружность

n

R

r

n = 3

а n - сторона

S n

n = 4

n = 6

Векторы

Правило

треугольника

Правило

параллелограмма

Сложение векторов

Вычитание векторов

Умножение вектора на число

Метод координат

• Координаты вектора.
• Нахождение координат вектора по координатам его начала и конца.
• Нахождение длины вектора по его координатам
• Нахождение длины отрезка по координатам его концов.
• Нахождение координат середины отрезка по координатам его концов.
• Уравнение прямой.
• Уравнение окружности

Нахождение координат вектора по координатам его начала и конца

У

О

Х

Каждая координата вектора равна разности

соответствующих координат его конца и начала.

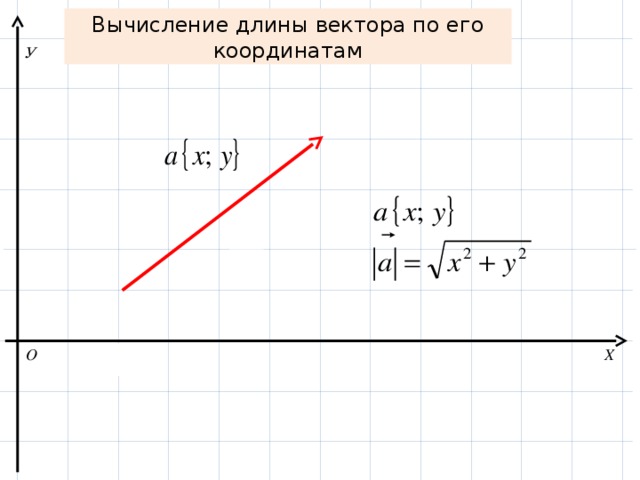
Вычисление длины вектора по его координатам

У

О

Х

Скалярное произведение векторов

Если векторы перпендикулярны, то скалярное произведение этих векторов равно 0.

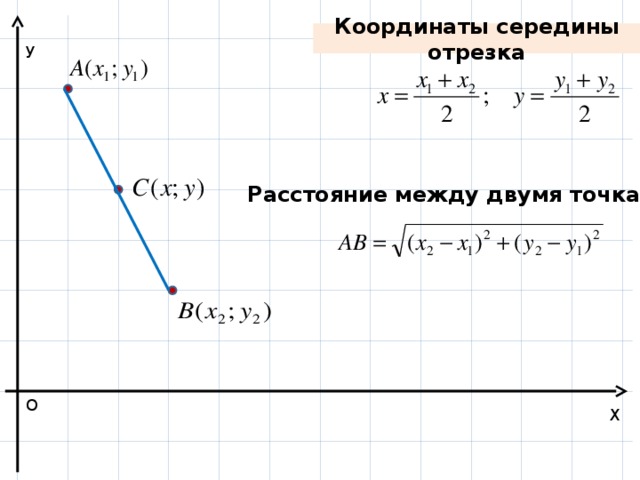
Координаты середины отрезка

У

Расстояние между двумя точками

О

Х

У

Уравнение окружности

r

Уравнение прямой

О

Х