«Город Таганрог»
Муниципальное общеобразовательное бюджетное учреждение
лицей №7
ПРОЕКТ
на тему:
«Платоновы тела или правильные многогранники»
(математика)
ученицы 9 «Б» класса
Матвиенко Дарьи Юрьевны
Руководитель проекта:
учитель математики
Гориславец Светлана Владимировна
г. Таганрог
2021 год
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ……………………………………………………………………….3
РАЗДЕЛ 1
1.1. Краткая история возникновения учения о правильных многогранниках ..4
1.2. Философия Платона………………………………………………………….5
РАЗДЕЛ 2
2.1. Многогранники……………………………………………………………….6
2.2. Правильные многогранники…………………………………………………7
2.3. Доказательство существования только пяти правильных многогранников………………………………………………………………...…8
РАЗДЕЛ 3
3.1. Свойства правильных многогранников……………………………………10
3.2. Формулы для правильных многогранников………………………………11
РАЗДЕЛ 4
4.1. Многогранники в искусстве .………………………………………………12
4.2. Правильные многогранники вокруг нас …………………………………..13
РАЗДЕЛ 5
5.1. Создание моделей многогранников ……………………………………….14
5.2. Опрос старшеклассников о знании понятия «Платоновы тела»…………15
ВЫВОД …………………………………………………………………………..16
СПИСОК ЛИТЕРАТУРЫ ………………………………………………………17
Платоновы тела или правильные многогранники
ВВЕДЕНИЕ
«Где материя, там геометрия»
Иоганн Кеплер
Нам известно, что геометрия – это наука, занимающаяся изучением фигур и их свойств в пространстве и на плоскости. Стереометрия же изучает свойства фигур в пространстве, а простейшими фигурами в пространстве считаются точки, прямые и плоскости. Более сложными пространственными фигурами, изучаемыми в стереометрии, являются многогранники. В проекте я уделяю внимание рассмотрению наиболее известных многогранников – правильных.
Гипотеза исследования: несмотря на ограниченное число правильных многогранников, роль их в науках и жизни очень велика.
Цели исследования:
- с помощью различных источников информации познакомиться с понятием Платоновы тела и узнать как можно больше всего, что с этим понятием связано;
- сделать модели правильных многогранников и провести опрос среди старшеклассников на знание Платоновых тел.
Задачи исследования:
- изучить понятие правильного многогранника, их виды и элементы;
- доказать существования ровно пяти правильных многогранников;
- рассмотреть свойства многогранников, формулы объемов и площадей поверхностей правильных многогранников;
- познакомиться с краткой историей возникновения теории многогранников и с философией Платона;
- показать существование правильных многогранников в других науках и искусстве;
Объект исследования: многогранники.
Предмет исследования: модели правильных многогранников в окружающем мире и их свойства.
Методы исследования:
- поисковый: поиск и систематизация данных из различных источников информации;
- практический: создание объёмных моделей изученных Платоновых тел;
- опрос: проведение опроса среди старшеклассников на знание понятия Платоновы тела;
- анализ: переработка полученных знаний и выделение главного;
- выводы: обобщение полученных знаний.
Итак, приступаем к изучению данной темы, которая показалась мне очень занимательной!
РАЗДЕЛ 1
1.1. Краткая история возникновения учения о правильных многогранниках
Правильные многогранники были известны людям с древнейших времён. Их вырезанные изображения можно найти на каменных шарах в Шотландии. В игральных костях, которыми пользовались люди на заре цивилизации, уже можно было рассмотреть формы правильных многогранников. Довольно подробно правильные многогранники были изучены древнегреческими учеными. По некоторым источникам честь их открытия принадлежит Пифагору. Другие же источники утверждают, что Пифагору были знакомы только тетраэдр, куб и додекаэдр, а открытие октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. Точно известно то, что Теэтет сумел дать математическое описание всех пяти правильных многогранников и первое известное доказательство того, что таких многогранников ровно пять. Интересно, что в XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы, исключая Землю, и правильными многогранниками. В своей книге «Тайна мира», вышедшей в 1596 году, он изложил свою модель Солнечной системы. Согласно этой модели, пять правильных многогранников помещались один в другой и разделялись рядами вписанных и описанных сфер. Каждая из шести таких сфер соответствовала одной из планет - Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну. Многогранники же в этой модели были расположены так: октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб (расположение перечислено от центра к краю). Таким образом, структура Солнечной системы и расстояния между планетами определялись правильными многогранниками. В последствии, ученым пришлось отказаться от оригинальной идеи Кеплера, но результатом его учения стало открытие двух законов, изменивших ранее известные знания по физике и астрономии, а также открытие правильных звёздчатых многогранников.
1.2. Философия Платона
 «Не геометр не войдет» - так было написано над воротами Академии Древнегреческого ученого и философа Платона (427 – 347 гг. до н.э.). Те, кто не был знаком с музыкой, геометрией и астрономией не принимались в платоновскую Академию. На правильных многогранниках построена философия Платона. Он писал об этих телах в своём трактате «Тимей» (360г до н. э.) В нём он сопоставил каждую из четырёх стихий: землю, воздух, воду и огонь определённому правильному многограннику. Огню - тетраэдр, земле — гексаэдр, воздуху — октаэдр, воде — икосаэдр. Такое сопоставление Платон пояснял следующим образом: «жар огня ощущается чётко и остро, как пирамидки-тетраэдры; мельчайшие компоненты воздуха - октаэдры настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков, к которым ближе всего икосаэдры; в противоположность воде, совершенно непохожие на шар кубики-гексаэдры составляют землю, которые являются причиной того, что земля рассыпается в руках, в противоположность плавному току воды». Относительно пятого элемента -додекаэдра, Платон сделал расплывчатое замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель же добавил пятый элемент — эфир. Он утверждал, что небеса сделаны из него, но он не относил этот элемент платоновскому пятому элементу. Аристотель подверг критике всю философию Платона о многогранниках. Но, тем не менее, во всемирной истории математики эти пять правильных многогранников известны как Платоновы тела.
«Не геометр не войдет» - так было написано над воротами Академии Древнегреческого ученого и философа Платона (427 – 347 гг. до н.э.). Те, кто не был знаком с музыкой, геометрией и астрономией не принимались в платоновскую Академию. На правильных многогранниках построена философия Платона. Он писал об этих телах в своём трактате «Тимей» (360г до н. э.) В нём он сопоставил каждую из четырёх стихий: землю, воздух, воду и огонь определённому правильному многограннику. Огню - тетраэдр, земле — гексаэдр, воздуху — октаэдр, воде — икосаэдр. Такое сопоставление Платон пояснял следующим образом: «жар огня ощущается чётко и остро, как пирамидки-тетраэдры; мельчайшие компоненты воздуха - октаэдры настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков, к которым ближе всего икосаэдры; в противоположность воде, совершенно непохожие на шар кубики-гексаэдры составляют землю, которые являются причиной того, что земля рассыпается в руках, в противоположность плавному току воды». Относительно пятого элемента -додекаэдра, Платон сделал расплывчатое замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель же добавил пятый элемент — эфир. Он утверждал, что небеса сделаны из него, но он не относил этот элемент платоновскому пятому элементу. Аристотель подверг критике всю философию Платона о многогранниках. Но, тем не менее, во всемирной истории математики эти пять правильных многогранников известны как Платоновы тела.
РАЗДЕЛ 2
2.1. Многогранники
Дадим общие понятия о многогранниках, которые понадобятся для изучения основной темы.
М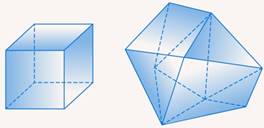 ногогранник – пространственное геометрическое тело, состоящее из конечного числа многоугольников.
ногогранник – пространственное геометрическое тело, состоящее из конечного числа многоугольников.
Грани многогранника – многоугольники, из которых состоит многогранник.
Ребра многогранника – стороны граней, из которых состоит многогранник.
Вершины многогранника – вершины граней, из которых состоит многогранник.
Диагональ многогранника – отрезок, соединяющий две вершины разных граней многогранника.
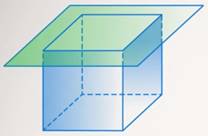 Выпуклый многогранник – многогранник, который располагается по одну сторону от плоскости любой его грани.
Выпуклый многогранник – многогранник, который располагается по одну сторону от плоскости любой его грани.

Невыпуклый многогранник – многогранник, у которого есть по крайней мере одна грань, через которую можно провести плоскость, которая поделит данный многогранник на две или более частей.
2.2. Правильные многогранники
«Правильных многогранников вызывающе мало,
но этот весьма скромный по численности отряд
сумел пробраться в самые глубины различных наук»
Л. Кэрролл
Приступим теперь к непосредственному изучению правильных многогранников. Дадим им определение и изучим их общие свойства.
Многогранник называется правильным, если он выпуклый, все грани его являются равными правильными многоугольниками и в каждой вершине его сходится одинаковое число рёбер. Надо пояснить что правильными называют многоугольники, у которых равны все стороны и все углы. Интересно, что под это определение в трёхмерном пространстве подходят всего пять многогранников. Их вид, название и основные характеристики приведены в таблице.
| Изображение | Название | Число вершин | Число рёбер | Число граней | Число сторон грани | Число рёбер, примыкающих к вершине |
|  | Тетраэдр | 4 | 6 | 4 | 3 | 3 |
|  | Гексаэдр | 8 | 12 | 6 | 4 | 3 |
|  | Октаэдр | 6 | 12 | 8 | 3 | 4 |
|  | Додекаэдр | 20 | 30 | 12 | 5 | 3 |
|  | Икосаэдр | 12 | 30 | 20 | 3 | 5 |
Заметим, что название каждого правильного многогранника происходит от следующих греческих слов: «эдра» - грань; «тетра» - четыре; «гекса» - шесть; «окта» - восемь; «икоса» - двадцать; «додека» - двенадцать. Дадим определения и рассмотрим внешний вид каждого правильного многогранника отдельно.
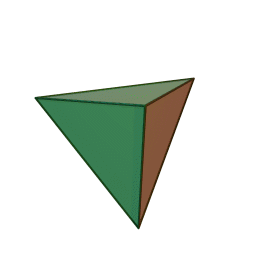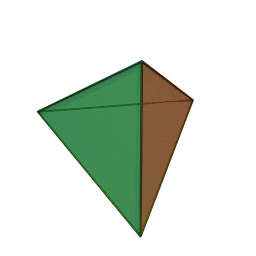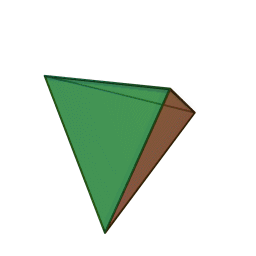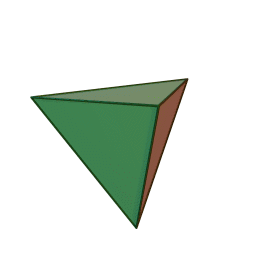 Правильный тетраэдр – это многогранник, состоящий из четырех равносторонних треугольников. Каждая его вершина есть вершина трех треугольников, следовательно, сумма углов при каждой его вершине равна 180 градусам.
Правильный тетраэдр – это многогранник, состоящий из четырех равносторонних треугольников. Каждая его вершина есть вершина трех треугольников, следовательно, сумма углов при каждой его вершине равна 180 градусам.
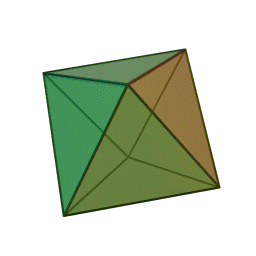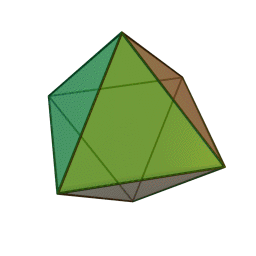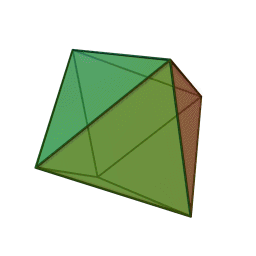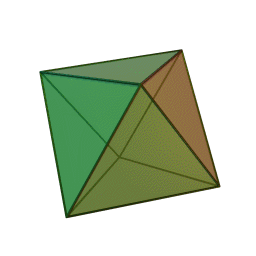
Правильный октаэдр – многогранник, состоящий из восьми равносторонних треугольников. Каждая вершина его является вершиной четырех треугольников, значит, сумма углов при каждой его вершине равна 240 градусам.

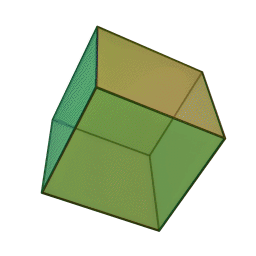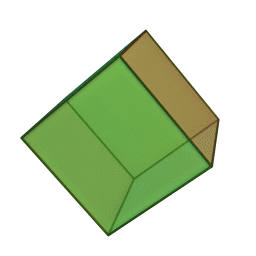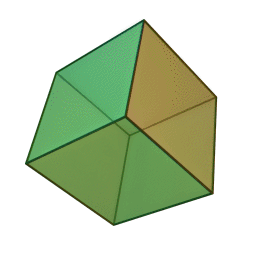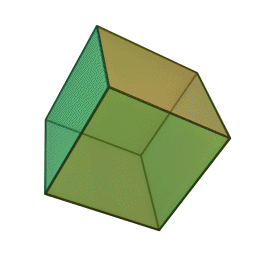 Куб (гексаэдр) – многогранник, состоящий из шести квадратов. Каждая вершина куба является вершиной трех квадратов, значит, сумма углов при каждой вершине куба равна 270 градусам.
Куб (гексаэдр) – многогранник, состоящий из шести квадратов. Каждая вершина куба является вершиной трех квадратов, значит, сумма углов при каждой вершине куба равна 270 градусам.

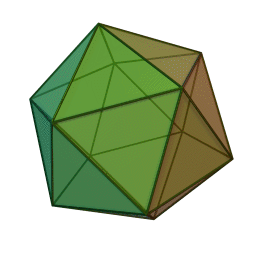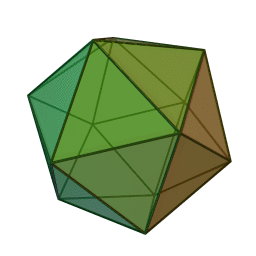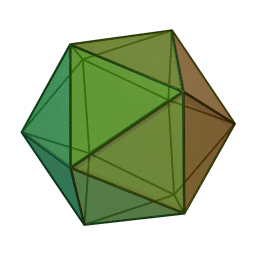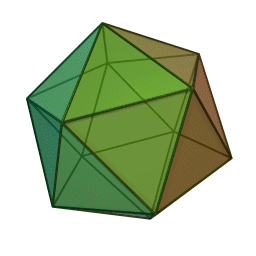 Правильный икосаэдр – многогранник, состоящий из двадцати равносторонних треугольников. Каждая вершина его является вершиной пяти треугольников, значит, сумма углов при каждой вершине икосаэдра равна 300 градусам.
Правильный икосаэдр – многогранник, состоящий из двадцати равносторонних треугольников. Каждая вершина его является вершиной пяти треугольников, значит, сумма углов при каждой вершине икосаэдра равна 300 градусам.
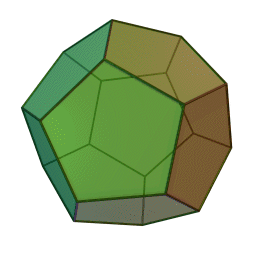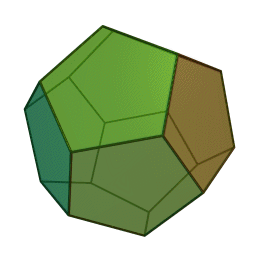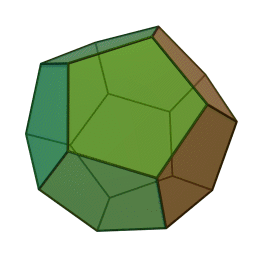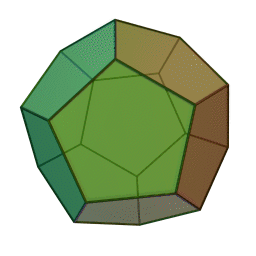

Правильный додекаэдр – многогранник, состоящий из двенадцати правильных пятиугольников. Каждая вершина его является вершиной трех правильных пятиугольников, следовательно, сумма углов при каждой вершине додекаэдра равна 324 градусам.

2.3. Доказательство существования только пяти правильных многогранников
Может показаться, что, как и правильных многоугольников, существует бесконечно много видов правильных многогранников. Но оказалось это не так. Можно доказать, что правильных многогранников существует ровно 5, то есть необходимо доказать, что не существует правильного многогранника, гранями которого являются правильные n-угольники при n≥6.
Докажем это.
Действительно, угол при вершине правильного n-угольника при n≥6 не меньше 1200. Но, с другой стороны, при каждой вершине многогранника должно быть не менее трех углов. Следовательно, если бы существовал правильный многогранник, с числом граней ≥6, то сумма углов его при каждой вершине была бы не меньше 3600. Но это невозможно, так как сумма всех углов при каждой вершине выпуклого многогранника меньше 3600. Таким образом получаем, что каждая вершина правильного многогранника может быть вершиной либо трех, либо четырех, либо пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников. Следовательно, не существует правильного многогранника, гранями которого являются n-угольники при n больше либо равном шести. Что и требовалось доказать.
РАЗДЕЛ 3
3.1. Свойства правильных многогранников
В 1750 году Эйлером была выведена формула, связывающая число вершин (В), число граней (Г) и число рёбер (Р) любого выпуклого многогранника простым соотношением:
В + Г = Р + 2
Сформулировать это соотношение можно следующим образом: «Сумма числа граней и числа вершин выпуклого многогранника равна числу его рёбер, увеличенному на 2». Это число получило название «эйлерова характеристика многогранника». Данная формула была уже в 1640 году выведена Декартом. Надо подчеркнуть, что формула Эйлера верна только для любых выпуклых многогранников.
Как и у любой геометрической фигуры, у многогранников можно определить площадь поверхности и объём.
Площадь поверхности многогранника – это сумма площадей всех его граней. Наглядно она равна площади развертки данного многогранника. Математическая формула {\displaystyle {R \over r}=\operatorname {tg} {\frac {\pi }{p}}\cdot \operatorname {tg} {\frac {\pi }{q}}.}площади поверхности правильного многогранника вычисляется, как площадь правильного n-угольника, умноженная на число граней n.
{\displaystyle S=\left({a \over 2}\right)^{2}\Gamma p\,\operatorname {ctg} {\frac {\pi }{p}}.}Объём же правильного многогранника равен объём правильной пирамиды, основанием которой служит правильный n-угольник, а высотой — радиус вписанной в нее сферы, умноженный на число граней этого многогранника. Отметим, что объем пирамиды равен произведению одной третьей площади её основания на высоту.
3.2. Формулы для правильных многогранников
Выпишем формулы объёмов и площадей поверхности для каждого из пяти правильных многогранников в виде таблицы для наглядности и удобства применения для решения задач на практике. В данной таблице a – это длина ребра многогранника.

РАЗДЕЛ 4
4.1. Многогранники в искусстве
В работах скульпторов, архитекторов, художников прослеживается большой интерес к формам правильных многогранников. Они восхищались совершенством, симметрией и гармонией многогранников. Так, например, Леонардо да Винчи увлекался теорией многогранников и часто изображал их на своих картинах. Известно, что он любил делать из дерева макеты правильных многогранников и дарить своим различным знаменитым знакомым.
Другим выдающимся художником эпохи Возрождения, увлекавшимся стереометрией, был Альбрехт Дюрер. На переднем плане его известной гравюры «Меланхолия» изображен додекаэдр.
На картине Сальвадора Дали «Тайная вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра.
Знаменитым примером XX века иллюстрации многогранников являются графические работы голландского художника М. К. Эшера. Например, на своей гравюре "Четыре тела" он изобразил пересечение правильных многогранников, которые как бы просвечиваются сквозь друг друга. А в его работе "Порядок и хаос" звездчатый додекаэдр занимает центральное место: он помещен внутрь стеклянной сферы, контрастируя с беспорядочно разбросанным по столу мусором.




4.2. Правильные многогранники вокруг нас
В основе кристаллической решетки многих веществ лежат формы правильных многогранников. Например, кристаллы всем известной поваренной соли имеют форму куба. Так же форму куба имеют кристаллические решётки многих металлов.
А вот молекулы газа метана, кристаллы белого фосфора, кристаллы сернокислого натрия имеет форму тетраэдра.
Такое устройство как уголковый отражатель имеет форму тетраэдра и используется для точного измерения расстояний при топографической съемке или при строительстве, а также для отражения светового излучения точно назад (катафот).
Кроме того, и молекулы воды имеют форму тетраэдра.
Знаменитая картонная упаковка, созданная в 1950 году компанией Tetra Pak для хранения молока, имела вид тетраэдра.
Самыми ценными считаются алмазы, имеющие форму октаэдра.
Форма икосаэдра оказалась очень удобной и привлекательной для живых существ. Например, одноклеточный организм Феодария по форме напоминает икосаэдр. Это объясняется тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Эта особенность помогает многим морским организмам преодолевать давление водной массы.
Вирусам важно управлять организмом, в котором они паразитируют, но размеры вируса ограничены. Поэтому для них также присуща форма икосаэдра.
А вот вирус полиомиелита имеет форму додекаэдра. Также, как и кристаллы пирита или сернистого колчедана, применяемого для получения особых сортов цемента, является природной моделью додекаэдра.
Кроме того, ученые полагают, что четырем геологическим эрам Земли соответствуют четыре каркаса правильных Платоновских тел: Протозою - тетраэдр (четыре плиты), Палеозою - гексаэдр (шесть плит), Мезозою - октаэдр (восемь плит), Кайнозою - додекаэдр (двенадцать плит).
В современной науке существует гипотеза, которую в начале 80-х гг. высказали московские инженеры Макаров и Морозов, согласно которой ядро Земли имеет форму и свойства растущего кристалла, который влияет на происхождение всех природных процессов, идущих на планете. Так вот силовое поле этого кристалла имеют икосаэдро-додекаэдровую форму.
РАЗДЕЛ 5
5.1. Создание моделей правильных многогранников
Если мы многогранник разрежем по нескольким его ребрам и разложим на плоскости, то получим его развертку. Надо учесть, что поверхность одного и того же многогранника может быть разрезана по-разному.
Удобнее всего при создании моделей многогранников из плоских разверток использовать развертки, в которых грани прилегают ребрами друг к другу, а объёмная модель конструируется загибанием развертки вдоль ребер. При создании моделей правильных многогранников я использовала следующие развертки:
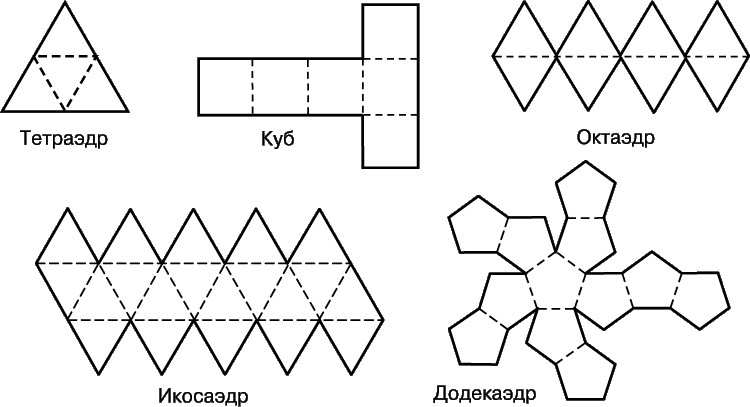
5.2. Результаты опроса учащихся 9 -11 классов о знании понятия «Платоновы тела»
В ходе проведения исследовательской работы у меня возникло желание узнать, известно ли старшеклассникам школы, в которой я учусь, понятие «Платоновы тела». Мной были опрошены ученики 9 – 11 классов. Полученные ответы я отобразила в виде диаграммы.
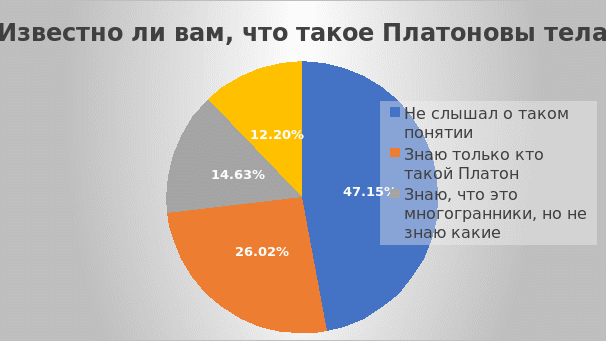
Таким образом, заметно, что большинству учеников не знакомо такое понятие, как Платоновы тела, хотя в жизни они могут часто с ними встречаться. После того, как учащиеся узнавали, что Платоновы тела – это правильные многогранники, многие начинали перечислять их названия.
ВЫВОД
Мною была выбрала данная тема, так как у мне возникло желание узнать, почему правильные многогранники издавна привлекали внимание учёных, философов, творческих и простых людей. Так же меня заинтересовала связь имени древнегреческого философа Платона с правильными многогранниками. Вызвали у меня интерес и количество Платоновых тел, и история их открытия. Я захотела сама сконструировать модели правильных многогранников и наглядно познакомиться с формой и особенностями строения каждого.
Мне было интересно работать над выбранной темой. Я получила новые для себя знания. Узнала о существовании правильных многогранников не только в мире математики и других наук, но и в окружающей природе. В том числе, я узнала об имеющих вид Платоновых тел кристаллических решётках многих веществ и молекулах некоторых живых организмов, например, вирусов и бактерий.
Для меня было неожиданностью, что многие знаменитые художники использовали в своих произведениях формы правильных многогранников. И это придает их работам дополнительный эффект и необычность.
Узнала о тесной связи математики и философии. В ходе работы я познакомилась с теорией московских инженеров, согласно которой силовое поле ядра Земли имеет икосаэдро-додекаэдровую форму, влияющую на многие процессы, происходящие на планете.
Благодаря полученным знаниям, я смогла сконструировать модели правильных многогранников, подготовила презентацию по теме «Платоновы тела или правильные многогранники», сделала брошюру на данную тему, в которой представила краткую справку о Платоне и таблицу с характеристикой каждого правильного многогранника.
Мною был проведен опрос старшеклассников о знании понятия «Платоновы тела». Результаты опроса я отобразила в виде диаграммы.
Я познакомилась с доказательством существования только пяти правильных многогранников, узнала причину названия каждого из них.
Закончить работу я бы хотела словами древнегреческого ученого Архимеда: «Геометрия показалась мне очень интересной и какой – то волшебной наукой». Я полностью согласна с его высказыванием!
СПИСОК ЛИТЕРАТУРЫ
Погорелов А. В. Геометрия. Учебное пособие для 7-11 классов. М., Просвещение, 2002.
Смирнова И. М. В мире многогранников. М., 1990.
Тихонов А. Н., Костомаров Д. П. Рассказы о прикладной математике. М.: Вита-Пресс, 2001.
Фридман Л. М. Изучаем математику, Москва, «Просвещение», 2002.
Интернет – ресурсы:
http://www.etudes.ru/data/localdocs/dolbilin_kvant1.pdf
http://www.etudes.ru/data/localdocs/dolbilin_kvant2.pdf
Многогранники.ru – сайт о создании моделей многогранников из бумаги https://www.mnogogranniki.ru/






 «Не геометр не войдет» - так было написано над воротами Академии Древнегреческого ученого и философа Платона (427 – 347 гг. до н.э.). Те, кто не был знаком с музыкой, геометрией и астрономией не принимались в платоновскую Академию. На правильных многогранниках построена философия Платона. Он писал об этих телах в своём трактате «Тимей» (360г до н. э.) В нём он сопоставил каждую из четырёх стихий: землю, воздух, воду и огонь определённому правильному многограннику. Огню - тетраэдр, земле — гексаэдр, воздуху — октаэдр, воде — икосаэдр. Такое сопоставление Платон пояснял следующим образом: «жар огня ощущается чётко и остро, как пирамидки-тетраэдры; мельчайшие компоненты воздуха - октаэдры настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков, к которым ближе всего икосаэдры; в противоположность воде, совершенно непохожие на шар кубики-гексаэдры составляют землю, которые являются причиной того, что земля рассыпается в руках, в противоположность плавному току воды». Относительно пятого элемента -додекаэдра, Платон сделал расплывчатое замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель же добавил пятый элемент — эфир. Он утверждал, что небеса сделаны из него, но он не относил этот элемент платоновскому пятому элементу. Аристотель подверг критике всю философию Платона о многогранниках. Но, тем не менее, во всемирной истории математики эти пять правильных многогранников известны как Платоновы тела.
«Не геометр не войдет» - так было написано над воротами Академии Древнегреческого ученого и философа Платона (427 – 347 гг. до н.э.). Те, кто не был знаком с музыкой, геометрией и астрономией не принимались в платоновскую Академию. На правильных многогранниках построена философия Платона. Он писал об этих телах в своём трактате «Тимей» (360г до н. э.) В нём он сопоставил каждую из четырёх стихий: землю, воздух, воду и огонь определённому правильному многограннику. Огню - тетраэдр, земле — гексаэдр, воздуху — октаэдр, воде — икосаэдр. Такое сопоставление Платон пояснял следующим образом: «жар огня ощущается чётко и остро, как пирамидки-тетраэдры; мельчайшие компоненты воздуха - октаэдры настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков, к которым ближе всего икосаэдры; в противоположность воде, совершенно непохожие на шар кубики-гексаэдры составляют землю, которые являются причиной того, что земля рассыпается в руках, в противоположность плавному току воды». Относительно пятого элемента -додекаэдра, Платон сделал расплывчатое замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель же добавил пятый элемент — эфир. Он утверждал, что небеса сделаны из него, но он не относил этот элемент платоновскому пятому элементу. Аристотель подверг критике всю философию Платона о многогранниках. Но, тем не менее, во всемирной истории математики эти пять правильных многогранников известны как Платоновы тела. ногогранник – пространственное геометрическое тело, состоящее из конечного числа многоугольников.
ногогранник – пространственное геометрическое тело, состоящее из конечного числа многоугольников. Выпуклый многогранник – многогранник, который располагается по одну сторону от плоскости любой его грани.
Выпуклый многогранник – многогранник, который располагается по одну сторону от плоскости любой его грани.





 Правильный тетраэдр – это многогранник, состоящий из четырех равносторонних треугольников. Каждая его вершина есть вершина трех треугольников, следовательно, сумма углов при каждой его вершине равна 180 градусам.
Правильный тетраэдр – это многогранник, состоящий из четырех равносторонних треугольников. Каждая его вершина есть вершина трех треугольников, следовательно, сумма углов при каждой его вершине равна 180 градусам.

 Куб (гексаэдр) – многогранник, состоящий из шести квадратов. Каждая вершина куба является вершиной трех квадратов, значит, сумма углов при каждой вершине куба равна 270 градусам.
Куб (гексаэдр) – многогранник, состоящий из шести квадратов. Каждая вершина куба является вершиной трех квадратов, значит, сумма углов при каждой вершине куба равна 270 градусам. Правильный икосаэдр – многогранник, состоящий из двадцати равносторонних треугольников. Каждая вершина его является вершиной пяти треугольников, значит, сумма углов при каждой вершине икосаэдра равна 300 градусам.
Правильный икосаэдр – многогранник, состоящий из двадцати равносторонних треугольников. Каждая вершина его является вершиной пяти треугольников, значит, сумма углов при каждой вершине икосаэдра равна 300 градусам.

















