Площадь поверхностей тел

Формулы площади поверхности тел

Площадь поверхности геометрической фигуры измеряется в квадратных единицах.  Очень часто используется в повседневной жизни, в строительстве, на производствах.  Например, нужно вам покрасить комнату, зная сколько краски используется на кв. метр,  и площади стен комнаты легко можно вычислить, сколько всего вам нужно купить краски.

Различают два вида площадей поверхности тел: S_бок — площадь боковой поверхности тела, и Р — площадь полной поверхности тела, которая равна сумме площадей боковой поверхности и основания тела.

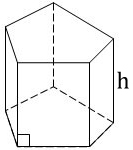
Формула площади поверхности призмы

Площадь боковой поверхности прямой призмы равна периметру основания умноженному на высоту призмы (высота=боковому ребру).

S_бок = ph=pl

р — периметр основания;

h — высота;

l — боковое ребро.

Формула площади поверхности куба

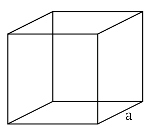Площадь боковой поверхности куба равна числу боковых граней умноженному на квадрат ребра.

S_бок = 4a²

Площадь полной поверхности куба равна числу всех граней куба умноженному на квадрат ребра.

P = 6a²

а — ребро куба.

Формула площади поверхности пирамиды

1) Правильная пирамида:

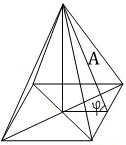S_бок = 1/2pA

p — периметр основания;

A — апофема.

S_бок = S/cos φ

S — площадь основания;

φ — угол между боковой гранью и основанием пирамиды.

S_бок = S_гр n

S_гр — площадь одной боковой грани;
n — количество боковых граней пирамиды.

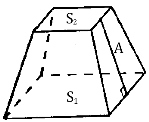2) Правильная усеченная пирамида:

S_бок = 1/2(p₁ + p₂)A

p₁ ,p₂ — периметры оснований;

A — апофема.

Р = S_бок + S₁ + S₂

Р — площадь полной поверхности правильной усеченной пирамиды;

S_бок — площадь боковой поверхности правильной усеченной пирамиды;

S₁ + S₂ — площади оснований.

Формула площади поверхности цилиндра

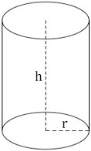S_бок = 2πrh = πdh

P = 2πr²+2πrh = 2π(r+h)

P — площадь полной поверхности цилиндра;

r — радиус цилиндра;

d — диаметр цилиндра;

h — высота цилиндра.

Формула площади поверхности конуса

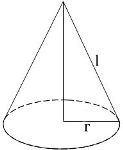
1) Прямой круговой конус:

S_бок = πrl = 1/2 πdl

P = πr² + πrl= πr(r+l)

P — площадь полной поверхности конуса;

r -радиус конуса;

d -диаметр конуса;

l — образующая конуса.

2) Усеченный прямой круговой конус:

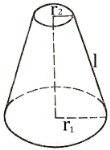
S_бок = πl(r₁ + r₂) = 1/2πl(d₁ + d₂)

P = πl(r₁ + r₂) + π(r₁ + r₂)

P — площадь полной поверхности усеченного конуса;

r₁, r₂ — радиусы оснований усеченного конуса;

d₁, d₂ — диаметры оснований усеченного конуса;

l — образующая усеченного конуса.

Формула площади поверхности шара (сферы)

Шар — тело, созданное вращением полукруга вокруг диаметра.

Сфера — поверхность шара.

P = 4πR² = πD²

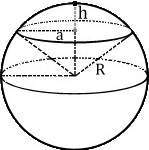
Формула площади поверхности сферического сегмента

Сферический сегмент — часть сферы, что отсекается от сферы плоскостью.

S_{сф. сегм.} = 2πRh = π(a² + h²)

Формула площади поверхности шарового сегмента

Шаровой сегмент — часть шара, что отсекается от шара плоскостью, и ограничивается кругом (основание шарового сегмента) и сферическим сегментом.

S_{шар. сегм.} = π(2Rh+a²)=π(h²+2a²)

R — радиус шара;

D — диаметр шара;

h — высота сегмента;

a — радиус основания сегмента.

Задачи:

Задание №1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.

Задание №2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 8. Найдите площадь ее поверхности.

Задание №3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 24, высота призмы равна 15. Найдите площадь ее поверхности.

Задание №4.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4, высота призмы равна 8. Найдите площадь ее поверхности.

Задание №5. Найдите площадь поверхности правильной четырехугольной пирамиды,  стороны основания которой равны 48 и высота равна 7.

Задание №6. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 40 и высота равна 15.

Задание №7 . Найдите площадь поверхности правильной четырехугольной пирамиды,  стороны основания которой равны 80 и высота равна 9..

Задание №8. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Задание №9. Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.

Задание №10. Ящик, имеющий форму куба с ребром 10 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.

Задание №11. Ящик, имеющий форму куба с ребром 20 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.