Площадь треугольника

Урок геометрии

8 класс

Тема урока: «Площадь треугольника»

Цели урока:

• Вывести формулы для вычисления площади треугольника и показать их применение в процессе решения задач.
• Совершенствовать навыки решения задач.

Не в количестве знаний заключается

образование, а в полном понимании

и искусном применении всего того,

что знаешь.

• Георг Гегель

4

5

8

11

5

3

2

5

7

2

12

Тема урока: «Площадь треугольника»

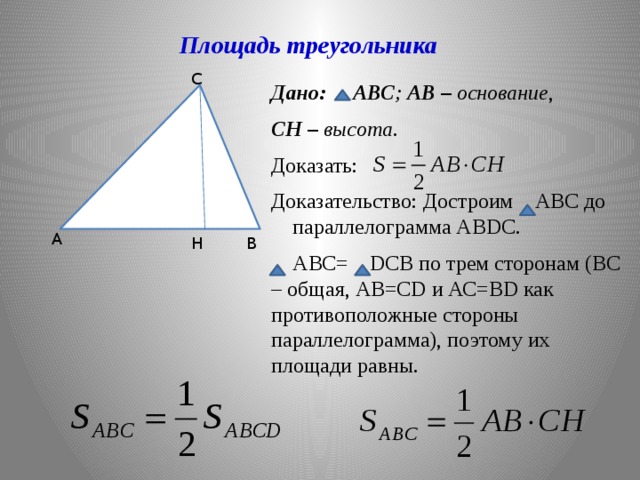
Площадь треугольника

С

Дано: АВС ; АВ – основание ,

СН – высота .

Доказать:

Доказательство: Достроим АBC до параллелограмма АВDC.

АВС= DCB по трем сторонам (ВС – общая, АВ=CD и АС=ВD как противоположные стороны параллелограмма), поэтому их площади равны.

А

Н

В

4

8

11

5

3

2

5

7

2

12

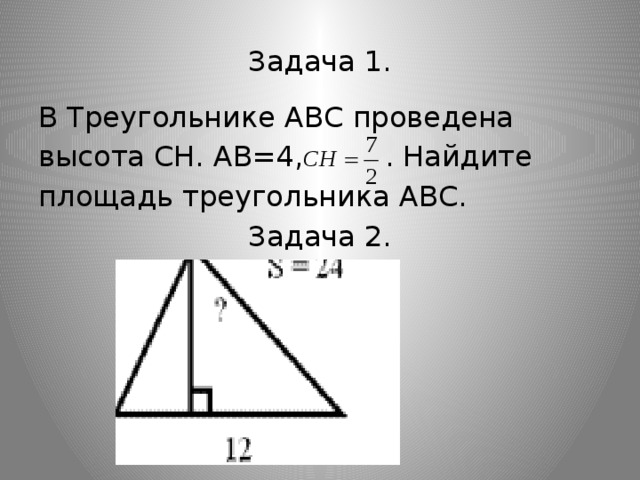
Задача 1.

В Треугольнике ABC проведена

высота СH. AB=4, . Найдите

площадь треугольника ABC.

Задача 2.

• В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.

2. Найдите площадь треугольника, изображённого на рисунке.

3. На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

Проверьте: 1) 25; 2) 84; 3) 16.

Оцените свою работу на уроке с помощью фраз:

- Сегодня на уроке я научился ….

-Я получил возможность научиться…

- Я пока еще не умею ….

- Я стал лучше понимать….

- Мне было сложно…

Домашнее задание п.52, № 468(а, в)

Дополнительная задача

Рекламная фирма для привлечения внимания решила сделать банерную растяжку треугольной формы АВС, закрепив вершину В на прямой, параллельной прямой АС. Удастся ли фирме сэкономить на материале, если будет изменяться только положение точки: а) В; б)С?

Спасибо за урок

Египетские пирамиды

Шаболовская телевизионная башня

Радиобашня Шухова — новаторская для XX века  гиперболоидная конструкция , выполненная в виде несущей стальной  сетчатой оболочки . Расположена в  Москве  на улице  Шухова . Построена в 1920—1922 годах по проекту академика  В. Г. Шухова

4

8

11

5

8

3

11

2

12

5

7

10

2