5 класс урок №106 27.02.18г
Наименьший общий знаменатель
Цели: формировать умения приводить дроби к наименьшему общему знаменателю различными способами и находить дополнительный множитель, решать задачи; развивать логическое мышление, память, трудолюбие.
Ход урока
I.Организационный момент
– Здравствуйте ребята!
Вот звенит для нас звонок – начинается урок. Ровно встали, подтянулись и друг другу улыбнулись.
Все улыбнулись и этим покажите, что у вас хорошее настроение, и вы готовы сегодня на уроке быть активными.
Приветствуют учителя, контролируют готовность к уроку, выполняют задание.
- проверка домашнего задания(что вы находили?)
II. Устный счет
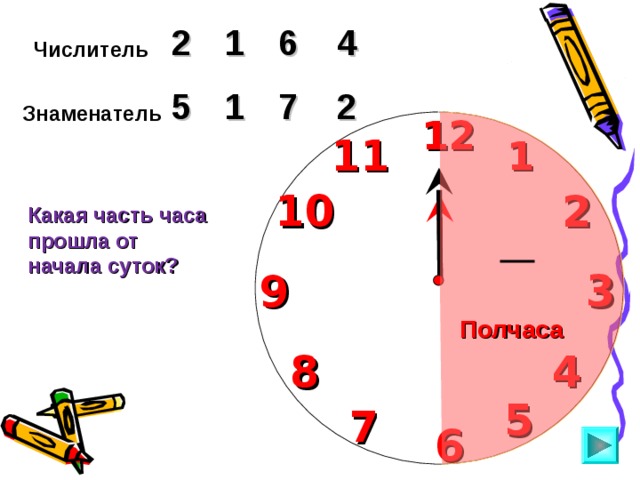
Найдите произведение чисел по готовым рисункам. (слайды 2,3,4)
Какой дробью еще можно записать 5/6? (слайд)
III. Актуализация знаний
1.Приведите дроби к знаменателю 36 (работа по слайу)
2.Приведите дроби к общему знаменателю 3/8 и 5/12 (назовие наименьший)
IV. Сообщение темы урока
— На прошлом уроке мы приводили дроби к новому знаменателю. Сегодня мы будем находить общий знаменатель для нескольких дробей и выясним, что такое наименьший общий знаменатель дробей.(слайд)
- Решение задачи
V. Изучение нового материала
1. Любые 2 дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.
— Найдите несколько общих знаменателей дробей. Назовите их наименьший общий знаменатель.
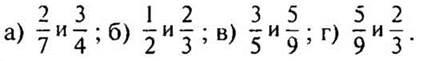
Общим знаменателем дробей может быть любое общее кратное их знаменателей.
При этом, как правило, стараются подобрать наименьший общий знаменатель (НОЗ) - тогда вычисления с дробями оказываются проще. Наименьший общий знаменатель равен наименьшему общему кратному знаменателей данных дробей.
2. Рассмотрим на примерах, как можно находить НОЗ дробей.
1) Приведем к общему знаменателю дроби 7/21 и 2/7.
— В чем особенность чисел 21 и 7? (21 делится нацело на 7.)
(Рассуждения приводит учитель.)
— Больший знаменатель — число 21 — делится на меньший знаменатель 7, следовательно, его можно взять в качестве общего знаменателя данных дробей. Этот общий знаменатель — наименьший из всех возможных.
Значит, нужно только дробь 2/7 привести к знаменателю 21. Для этого найдем дополнительный множитель: 21 : 7 = 3. 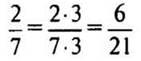
— Какой вывод можно сделать? (Если один знаменатель дроби делится на другой, то НОЗ будет больший знаменатель.)
2) Приведем к общему знаменателю дроби 3/4 и 2/5.
— Что можете сказать о числах 4 и 5? (Числа взаимно простые.) Общий знаменатель данных дробей должен делиться и на 4, и на 5, т.е. быть их общим кратным. Общих кратных 4 и 5 бесконечно много: 20, 40, 60, 80 и т. д. Наименьшее кратное число 20 — произведение 4 и 5.
Значит, нужно привести каждую из дробей к знаменателю 20: 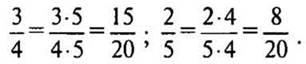
— Какой вывод можно сделать? (Если знаменатели дробей взаимно простые числа, то наименьшим общим знаменателем будет их произведение.)
3)3/4 и 1/6
— Какой вывод можно сделать?
VI. Физкультминутка
VII. Коллективное выполнение упражнений(слайд)
Работа над задачей
— О ком идет речь в задаче?
VIII. Закрепление изученного материала
1Работа в парах по карточкам.
Отвечает учителю кто-то один от пары.
2. № 799 (а—е) (с подробным комментарием у доски и в тетрадях, а) б) записать решение подробно, затем это все проговаривать устно, записывать только дроби с новым знаменателем).
3. Назовите числа, которые:
а) больше 4/7, но меньше 5/7; б) больше 1/6, но меньше 2/6; в) больше 5/8, но меньше 3/4.
— Что нужно сделать, чтобы выполнить задание? (Привести дроби к новому знаменателю.)
VIII. Самостоятельная работа
Вариант I
1. Приведите дроби к новому знаменателю 24: 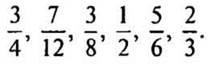
2. Приведите дробь 3/5 к новому знаменателю: 15; 25; 40; 55; 250; 300.
Вариант II
1. Приведите дроби к новому знаменателю 48: 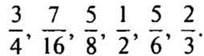
2. Приведите дробь 4/7 к новому знаменателю: 14; 28; 49; 70; 210; 350.
Вариант III (для более подготовленных учащихся)
1. Приведите дроби к новому знаменателю 84: 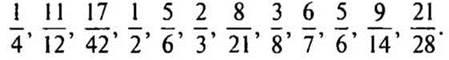
2. Приведите дробь 5/8 к новому знаменателю: 16; 24; 56; 80; 240; 3200.
IX. Подведение итогов урока. Рефлексия.
— Какое число может служить общим знаменателем двух дробей?
— Как привести дроби к наименьшему общему знаменателю?
— На каком свойстве основано правило приведения дробей к общему знаменателю?
Домашнее задание:
П.4.4 выучить правило№799 (д,е), 300 (г,е), 800(а,б), 803 (б)





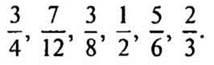
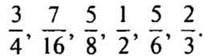
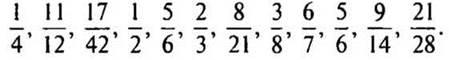
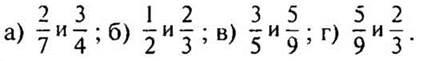
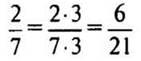
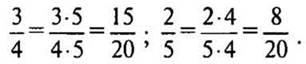
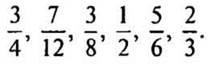
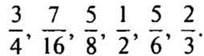
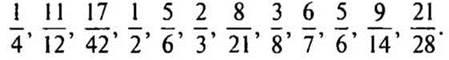









 . Значит девочек в классе больше." width="640"
. Значит девочек в классе больше." width="640"






















