Образцы решения задач
Решение задач уровня В
Задача 1. Высота правильной треугольной призмы равна 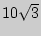 . Секущая плоскость проходит через среднюю линию нижнего основания и параллельную ей сторону верхнего основания и составляет с плоскостью нижнего основания двугранный угол величиной
. Секущая плоскость проходит через среднюю линию нижнего основания и параллельную ей сторону верхнего основания и составляет с плоскостью нижнего основания двугранный угол величиной 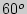 . Найдите площадь сечения призмы данной плоскостью.
. Найдите площадь сечения призмы данной плоскостью.
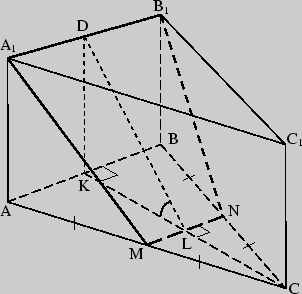
Решение: Сечением призмы является равнобедренная трапеция MA B
B N, так как
N, так как 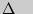 А
А М =
М = 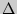 ВВ
ВВ N по двум катетам.
N по двум катетам.
MN 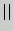 АВ как средняя линия
АВ как средняя линия  АВС:
АВС:
MN = 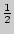 АВ =
АВ = 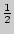 A
A B
B ;
;
В 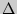 АВС KL = LC =
АВС KL = LC = 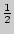 KC; КС = АВ
KC; КС = АВ 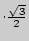 ; KL = АВ
; KL = АВ 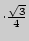 ;
;
В 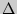 DKL: KL =
DKL: KL = 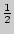 DL (так как
DL (так как 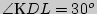 ); DL = 2
); DL = 2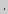 KL = АВ
KL = АВ 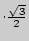 ;
;
DL = 20;
Ответ: 200 .
.
Задача 2. Найдите объем правильной четырехугольной пирамиды с апофемой, равной  , если ее боковое ребро составляет угол
, если ее боковое ребро составляет угол  с плоскостью основания.
с плоскостью основания.
Решение:
SM - апофема боковой грани.
По теореме о трех перпендикулярах
OM  DC; OM =
DC; OM = 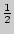 AD.
AD.
Обозначим высоту пирамиды  ,
,
сторону основания  .
.
В 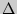 SOС:
SOС:  ; ОS =
; ОS = 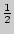 SС,
SС,
ОС = ОS  .
.
В 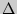 ADС: АС = AD
ADС: АС = AD  ;
;
ОС = AD  . Тогда,
. Тогда,  .
.
В 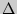 SOM: SM
SOM: SM = SO
= SO + OM
+ OM ;
;  ;
;
Составим систему уравнений:
Преобразуем систему к виду:
Решим систему уравнений методом подстановки:
Объем пирамиды  : V =
: V =  24
24 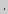 2 = 16. Ответ: 16.
2 = 16. Ответ: 16.
Задача 3. Найдите площадь осевого сечения конуса, если высота конуса равна 4, а площадь полной поверхности конуса  .
.
Решение:
Осевым сечением конуса является равнобедренный треугольник ASB:  =
=  AB
AB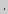 SO =
SO =  2
2  .
.
Площадь полной поверхности конуса вычисляется по формуле  .
.
 ; по условию
; по условию  = 24
= 24 .
.
Следовательно,  = 24;
= 24;  = 24 (*).
= 24 (*).
В 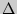 SOВ:
SOВ:  ;
;  ; (
; ( -
-  = 16.
= 16.
Составим систему уравнений: ;  .
.
Подставим найденное значение  в уравнение (*):
в уравнение (*):
= 9;  = 3;
= 3;  = 3
= 3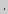 4 =12. Ответ: 12.
4 =12. Ответ: 12.
Задача 4. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус основания цилиндра  равен 15, длина отрезка АВ = 12
равен 15, длина отрезка АВ = 12 , а угол между прямой АВ и плоскостью основания цилиндра равен
, а угол между прямой АВ и плоскостью основания цилиндра равен  . Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки А и В.
. Найдите расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки А и В.
Решение:
ADBC - плоскость, параллельная оси  и перпендикулярная плоскости основания цилиндра.
и перпендикулярная плоскости основания цилиндра.
Искомое расстояние - длина отрезка О Р;
Р;
О Р
Р  AD;
AD;  ;
;
;
АР = РD = 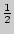 AD =
AD = 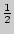 ВС = 9;
ВС = 9;
O D =
D =  = 15, следовательно, О
= 15, следовательно, О Р =
Р =  = 12. Ответ: 12.
= 12. Ответ: 12.
Задача 5. В треугольной пирамиде SABC с вершиной S ребра SA, SB, SC взаимно перпендикулярны и имеют длины соответственно 8, 6, 3. В пирамиду вписан куб, три грани которого лежат на гранях пирамиды, содержащих вершину S, а одна из вершин куба лежит на грани ABC. Найдите длину ребра куба.
Решение:
Решим задачу координатным методом. Пусть начало координат совпадает с вершиной S, а оси координат содержат ребра SA, SB, SC. Тогда точки S, A, B, С имеют координаты соответственно (0;0;0), (8;0;0), (0;6;0), (0;0;3). Уравнение плоскости АВС в отрезках в соответствии с общей формулой  имеет вид:
имеет вид:

Пусть ребро куба равно  . Тогда в плоскости АВС будет располагаться вершина куба, имеющая координаты (
. Тогда в плоскости АВС будет располагаться вершина куба, имеющая координаты ( ;
;  ;
;  . Подставим координаты этой вершины в уравнение плоскости АВС:
. Подставим координаты этой вершины в уравнение плоскости АВС:  .
.
Следовательно,  , откуда
, откуда  = 1,6.
= 1,6.
Ответ: 1,6.
Решение задач уровня С
Задача: В кубе ABCDA B
B C
C D
D со стороной, равной 2, на ребрах AD, DC, CC
со стороной, равной 2, на ребрах AD, DC, CC заданы соответственно точки M, N, L, причем AM=1, DN=1, CL =
заданы соответственно точки M, N, L, причем AM=1, DN=1, CL =  . Вокруг куба описан шар.
. Вокруг куба описан шар.
Определите площадь круга - сечения шара плоскостью, проходящей через точки M, N, L
Решение: Данная задача может быть решена различными способами.
1. Аналитико-синтетический способ:
Центр описанного шара совпадает с центром куба, а его радиус - с половиной диагонали куба. Длина диагонали куба 2 . Радиус шара
. Радиус шара  равен
равен  .
.
Чтобы найти площадь сечения шара указанной в условии плоскостью, удобнее определить сначала расстояние  от центра шара до заданной плоскости. Тогда
от центра шара до заданной плоскости. Тогда  - радиус сечения можно выразить из условия
- радиус сечения можно выразить из условия  , а искомая площадь находится по формуле
, а искомая площадь находится по формуле  .
.
Рассмотрим два чертежа: пространственный и выносной.
Чтобы построить сечение куба плоскостью, последовательно выполняем следующие действия:
1. Проводим прямую MN, обозначаем точки пересечения прямой MN с продолжениями ребер ВА и ВС (соответственно F и Р) и с диагональю BD (точка Q).
Доказываем, что BQ = 3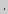 QD.
QD.
2. Строим прямую PL, обозначаем точку пересечения прямой PL с ребром BB - т. K.
- т. K.
Доказываем, что т. К - середина ВВ .
.
3. Соединяем точки K и F, KF  AA
AA = E.
= E.
4. Соединяем точки E и M, L и N. Искомое сечение - пятиугольник EKLNM.
Теперь рассмотрим сечение куба плоскостью BB D
D D, сохраняя введенные обозначения (выносной чертеж):
D, сохраняя введенные обозначения (выносной чертеж):
КО = 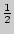 ВD =
ВD =  АВ
АВ  ;
;
KQ = BK
= BK + BQ
+ BQ ;
;
KQ ;
3)  ;
;
4)  ;
;
5) ; 6)  .
.
2. Координатный способ
Рассмотрим систему координат, совмещенную с заданным кубом. Разместим начало координат в точке D(0;0;0). Пусть ось О содержит ребро DА, точка М(0;1;0); ось О
содержит ребро DА, точка М(0;1;0); ось О содержит ребро DС, точка N(1;0;0); ось О
содержит ребро DС, точка N(1;0;0); ось О содержит ребро DD
содержит ребро DD , точка L(2;0;
, точка L(2;0;  .
.
Центр куба и описанного шара имеет координаты (1;1;1). Составим уравнение плоскости LMN и найдем  как расстояние от точки (
как расстояние от точки ( до плоскости
до плоскости
A + B
+ B + C
+ C + D = 0.
+ D = 0.
по формуле:
Составим систему уравнений для определения коэффициентов в уравнении плоскости, используя координаты точек L, M, N:
-3А = 3D.
Составим уравнение плоскости LMN: - D - D
- D + 3D
+ 3D + D = 0.
+ D = 0.
Разделив на (-D), получим уравнение плоскости  - 3
- 3 - 1 = 0. Легко убедиться подстановкой, что координаты точек L, M, N удовлетворяют полученному уравнению плоскости.
- 1 = 0. Легко убедиться подстановкой, что координаты точек L, M, N удовлетворяют полученному уравнению плоскости.
Подставим найденные величины в формулу расстояния от точки до плоскости:
Следовательно, площадь сечения равна  . Ответ:
. Ответ:  .
.

Подраздел
Домашнее задание № 2
Задачи уровня В
1. В основании пирамиды лежит равнобедренный треугольник с боковой стороной 2 и основанием 2,4. Боковые ребра пирамиды наклонены к плоскости основания под углом  . Найдите объем пирамиды. Ответ:
. Найдите объем пирамиды. Ответ:  1,2.
1,2.
2. Угол при вершине осевого сечения конуса равен 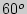 , а радиус описанной около конуса сферы равен 6. Найдите площадь боковой поверхности конуса. Ответ:
, а радиус описанной около конуса сферы равен 6. Найдите площадь боковой поверхности конуса. Ответ:  .
.
3. Высота цилиндра равна 16, радиус основания 10. Концы отрезка КМ, не являющегося образующей цилиндра, лежат на окружностях его оснований. Расстояние между осью цилиндра и параллельной ей плоскостью, проходящей через точки К и М, равно 6. Найдите угол в градусах между прямой КМ и плоскостью основания цилиндра.
Ответ:  .
.
Задача уровня С
4. В кубе ABCDA B
B C
C D
D со стороной 1 на ребрах AB, AD, CC
со стороной 1 на ребрах AB, AD, CC заданы соответственно точки M, N, L, причем AM =
заданы соответственно точки M, N, L, причем AM =  , AN =
, AN =  , CL =
, CL = 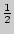 . В куб вписан шар. Определите площадь круга - сечения шара плоскостью, проходящей через точки M, N, L
. В куб вписан шар. Определите площадь круга - сечения шара плоскостью, проходящей через точки M, N, L
Ответ:  .
.
3


















