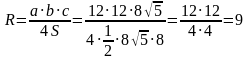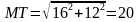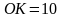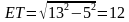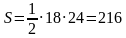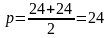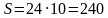Подготовка к контрольной работе

Дата:

Тема: Подготовка к контрольной работе

Задачи: обобщить и систематизировать теоретически знания и умения решать задачи по теме.

Ход урока

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Если около четырехугольника можно описать окружность, то его площадь равна

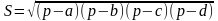
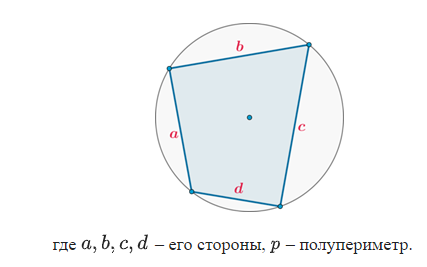
Если в четырехугольник можно вписать окружность, то его площадь равна

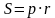
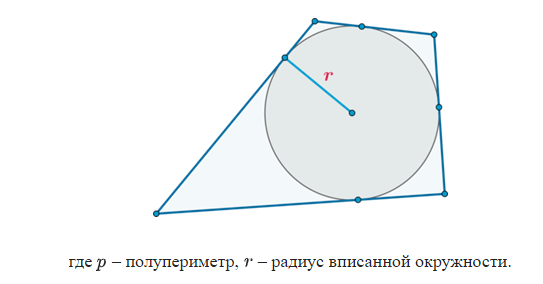
1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Задача 1. Равносторонний треугольник KME вписан в окружность радиуса 5. Найти сторону треугольника.

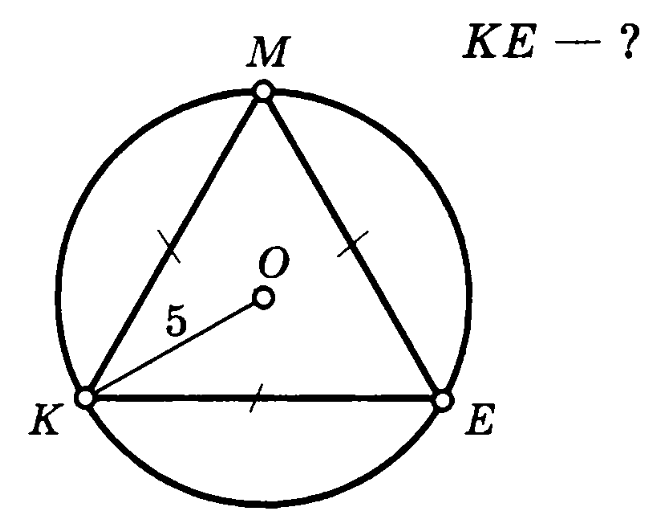
Решение (краткое). Воспользуемся формулой для радиуса описанной окружности около равностороннего треугольника:

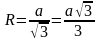
Преобразуем её в формулу для нахождения стороны:

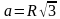
Тогда сторона треугольника:

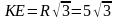
Ответ: .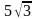

Задача 2. Равнобедренный треугольник QMT вписан в окружность. Высота треугольника MN=8, боковая сторона QM=MT=12. Найти радиус окружности.

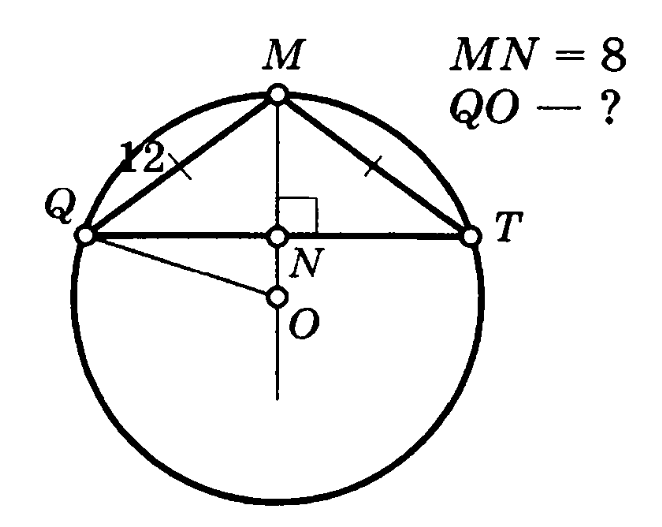
Решение (краткое). Найдем QN из треугольника QMN:

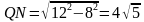
Тогда сторона QT= .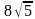

Применим формулу для нахождения радиуса описанной окружности:

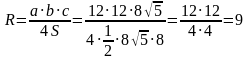
Ответ: 9

Задача 3. Треугольник MKT вписан в окружность, угол MKT опирается на диаметр. Стороны треугольника KM=12, KT=16. Найти радиус окружности.

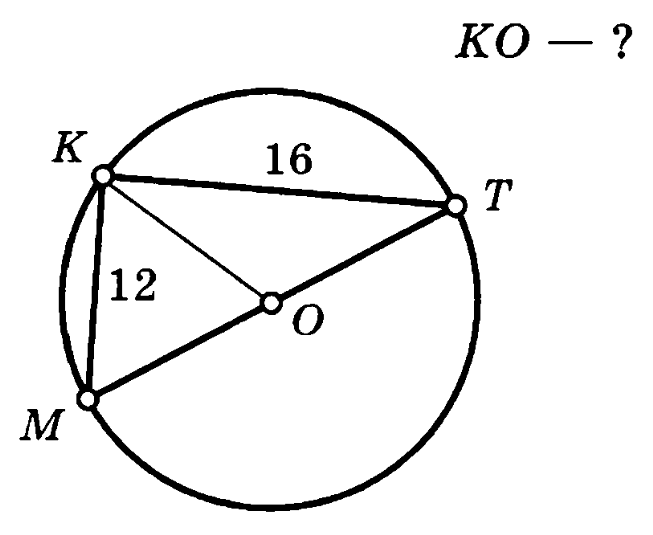
Решение (краткое). Найдем длину стороны MT:

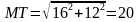
Т.к. MT – это диаметр окружности, то радиус вдвое меньше.

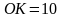
Ответ: 10.

Задача 4. Равнобедренный треугольник REF вписан в окружность. Центр окружности делит высоту треугольника RS на отрезки RO=13 и OT=5. Найти площадь треугольника REF.

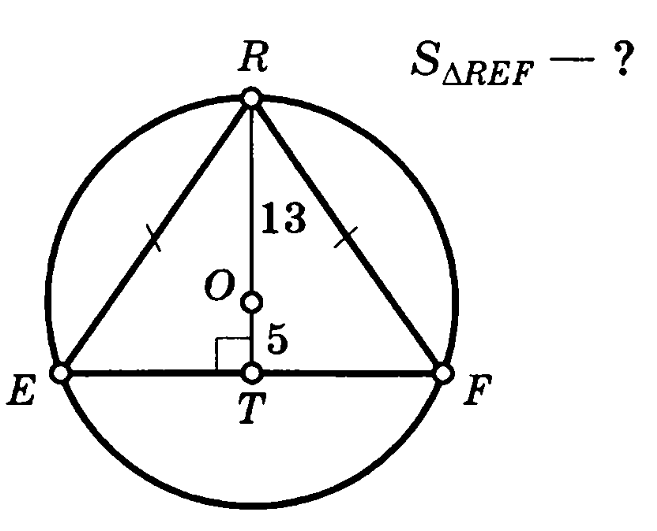
Решение (краткое). RO=OE=OF=13. Найдем ET:

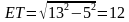
Тогда сторона EF=2ET=24.

Найдем площадь треугольника:

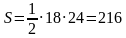
Ответ: 216.

Задача 5. В четырехугольник ABCD вписана окружность радиуса 10. Сумма противоположных сторон четырехугольника равна 24. Найти площадь четырехугольника.

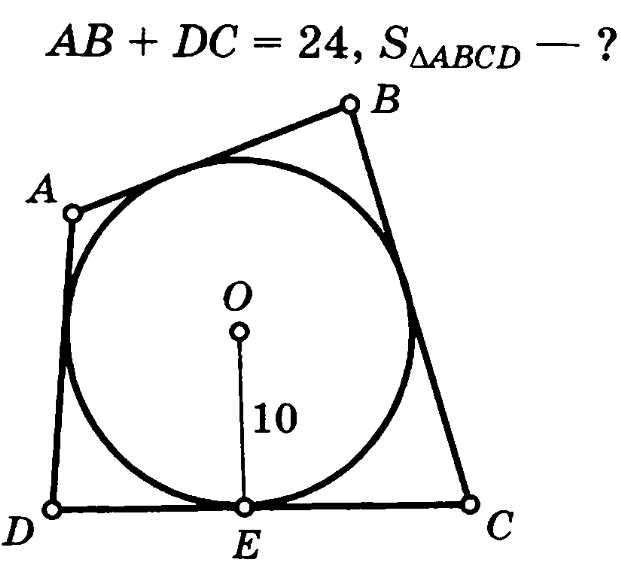
Решение (краткое). Найдем площадь четырехугольника по формуле .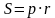

По свойству AB+DC=AD+BC=24, тогда полупериметр равен:

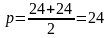
Тогда

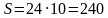
Ответ: 240.

Задача 6. Прямоугольник ABCD вписан в окружность. Меньшая из его сторон равна 10, а тупой угол между диагоналями равен 120°. Найти радиус окружности.

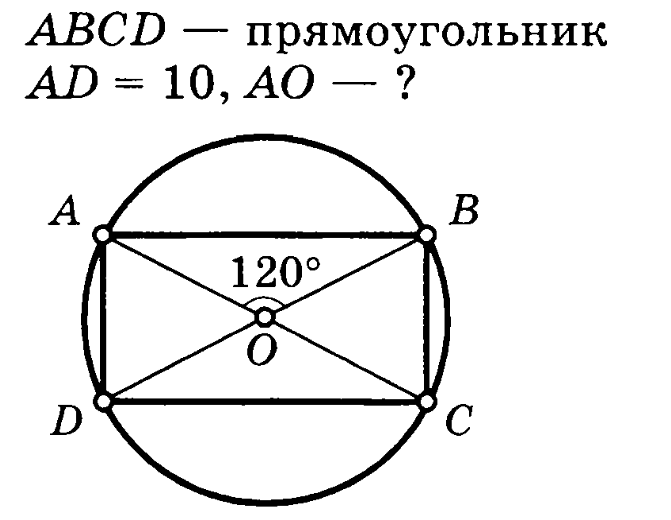
Решение (краткое). Угол AOD=60°, AO=DO, следовательно, треугольник AOD равносторонний. AO=10.

Ответ: 10.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: подготовиться к контрольной работе, вспомнить теорию и решения задач.
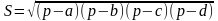
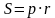
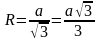
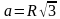
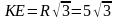
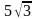
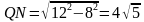
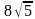