Подготовка к профильному ЕГЭ по математике. Задание 3.

Задание 3 (ЕГЭ профиль).

1. Площадь большого круга шара равна 1. Найдите площадь поверхности шара.

2. Площадь поверхности шара равна 20. Найдите площадь большого круга шара.

3. Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 80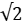 . Найдите площадь боковой поверхности конуса.

4. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 23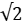 . Найдите радиус сферы.

5. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен 86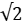 . Найдите образующую конуса.

6. Шар вписан в цилиндр. Площадь поверхности шара равна 170. найдите площадь полной поверхности цилиндра.

7. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 192. Найдите объём конуса.

8. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 48.

9. Шар, объём которого равен 90, вписан в цилиндр. Найдите объём цилиндра.

10. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 87. Найдите площадь поверхности шара.

11. Найдите объём многогранника, вершинами которого являются точки A, C, D, A₁, C₁, D₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого AB = 3, AD = 4, AA₁ = 7.

12. Найдите объём многогранника, вершинами которого являются точки C, D, B₁, D₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого AB = 10, AD = 9, AA₁ = 5.

13. Найдите объём многогранника, вершинами которого являются точки A, C, D, A₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого AB = 7, AD = 6, AA₁ = 9.

14. Найдите объём многогранника, вершинами которого являются точки A, B, C, A₁ правильной треугольной призмы ABCA₁B₁C₁, у которой площадь основания равна 8, а боковое ребро равно 6.

15. Найдите объём многогранника, вершинами которого являются точки A, B, C, A_1, B_1, C₁ правильной треугольной призмы ABCA₁B₁C₁, у которой площадь основания равна 6, а боковое ребро равно 7.

16. Найдите объём многогранника, вершинами которого являются точки B, A_1, B_1, C₁, D₁, E₁, F₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 3, а боковое ребро равно 3.

17. Найдите объём многогранника, вершинами которого являются точки A_, B_, C, D, E, F, C₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 7, а боковое ребро равно 9.

18. Найдите объём многогранника, вершинами которого являются точки B_, C, D, E, B₁, C_1, D₁, E₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 12, а боковое ребро равно 7.

19. Дано два цилиндра. Объем первого цилиндра равен 81. У второго цилиндра высота в 4 раза больше, а радиус в 3 раза меньше, чем у первого. Найдите объём второго цилиндра.

20. Дано два цилиндра. Объем первого цилиндра равен 45. У второго цилиндра высота в 3 раза больше, а радиус в 2 раза меньше, чем у первого. Найдите объём второго цилиндра.

21. Даны два шара. Радиус первого шара в 70 раз больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

22. Во сколько раз уменьшится объём конуса, если его высота уменьшится в 8,5 раза, а радиус основания останется прежним?

23. Во сколько раз увеличится объём конуса, если его радиус основания увеличится в 26 раз, а высота останется прежней?

24. Во сколько раз увеличится объём шара, если его радиус увеличится в 7 раз?

25. Через среднюю линию основания треугольной призмы, объём которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.

26. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объём этой призмы, если отсечённой треугольной призмы равен 5,5.

27. Объём правильной четырёхугоной пирамиды SABCD равен 152. точка E - середина ребра SB. Найдите объём треугольной пирамиды EABC.

28. От треугольной пирамиды, объём которой равен 44, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объём отсечённой треугольной пирамиды.

29. Объём треугольной пирамиды равен 36. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 7 : 5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.

30. Длина окружности основания цилиндра равна 4, высота равна 7. Найдите площадь боковой поверхности цилиндра.

31. Длина окружности основания конуса равна 5, образующая равна 10. Найдите площадь боковой поверхности конуса.

32. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 15 раз, а радиус основания останется прежним?

33. Во сколько раз уменьшится площадь боковой поверхности конуса, если его радиус основания уменьшится в 28 раз, а образующая останется прежней?

34. Во сколько раз увеличится площадь поверхности октаэдра, если все его рёбра увеличатся в 17 раз?

35. Ребро правильного тетраэдра равно 6. Найдите площадь сечения, проходящего через середины четырёх его рёбер.

36. Объём куба равен 123. Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной - центр куба.

37. Найлите объём параллелепипеда ABCDA₁B₁C₁D₁, если объём треугольной пирамиды ABDA₁ равен 5.

38. В цилиндрическом сосуде уровень жидкости достигает 98 см. На какой высоте будет находится уровень жидкости, если её перелить в цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.

39. В сосуд, имеющий форму конуса (вершина конуса внизу), налили 50 мл жидкости до половины высоты конуса. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?

40. Объём цилиндра равен 12. Чему равен объём конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?

41. Шар, объём которого равен 42ℼ, вписан в куб. Найдите объём куба.

42. Объём данного правильного тетраэдра равен 64. Найдите объём правильного тетраэдра, ребро которого в 2 раза меньше ребра данного тетраэдра.

43. В правильной четырёхугольной пирамиде SABCD точка O - центр основания, S - вершина, SO = 8, SB = 10. Найдите длину отрезка BD.

44. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке P. площадь треугольника ABC равна 8, объём пирамиды равен 48. Найдите длину отрезка PS.

45. В правильной треугольной пирамиде SABC Q - середина ребра AB, S - вершина. Известно, что SQ = 28, а площадь боковой поверхности равна 294. Найдите длину отрезка BC.

46. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке K. Объём пирамиды равен 70. KS = 21. Найдите площадь треугольника ABC.

47. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны D₁B = √77, BB₁ = 5, B₁C₁ = 6. Найдите длину ребра A₁B₁.

48. Высота конуса равна 7, а диаметр основания - 48. Найдите образующую конуса.

49. Диаметр основания конуса равен 30, а длина образующей - 17. Найдите высоту конуса.

50. Площадь боковой поверхности цилиндра равна 56ℼ, а диаметр основания - 8. Найдите высоту цилиндра.

51. Площадь боковой поверхности цилиндра равна 45ℼ, а высота - 5. Найдите диаметр основания.

52. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны A₁B₁ = √92, AA₁ = 4, A₁D₁ = 6. Найдите длину диагонали D₁B.

53. Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом 30⁰. Боковое ребро равно 3. Найдите диагональ призмы.

54. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB = 27, AA₁ = 10, AD = 36. Найдите площадь сечения, проходящего через вершины D, D₁, B.

55. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 9. Найдите объём параллелепипеда.

56. Прямоугольный параллелепипед описан около сферы радиуса 6. Найдите его объём.

57. В цилиндрический сосуд налили 3000 см³ воды. Уровень воды при этом достигает 15 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 6 см. Чему равен объём детали? Ответ выразите с см³.

58. В цилиндрическом сосуде уровень жидкости достигает 45 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй сосуд, диаметр основания которого в 3 раза больше первого?

59. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 4 см. На какой высоте будет находиться уровень воды, если её перелить в другой такой же сосуд, у которого сторона основания в 2 раза больше, чем у первого?

60. В сосуд, имеющий форму правильной треугольной призмы, налили 1400 см³ воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объём детали. Ответ дайте в см³.

61. В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра равны 2/ℼ. Найдите объём цилиндра, описанного около этой призмы.

62. В основании прямой призмы лежит квадрат со стороной 4. Боковые рёбра равны 9/ℼ. Найдите объём цилиндра, описанного около этой призмы.

63. Цилиндр и конус имеют общее основание и общую высоту. Найдите объём цилиндра, если объём конуса равен 40.

64. Объём конуса равен 48. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же высотой. Найдите объём меньшего конуса.

65. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в два раза?

66. Объём одного куба в 8 раз больше объёма другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

67. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь поверхности равна 248. Найдите боковое ребро этой призмы.

68. Через среднюю линию основания треугольной наклонной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

69. Во сколько раз увеличится площадь поверхности пирамиды, если все её рёбра увеличить в 2 раза?

70. В правильной четырёхугольной пирамиде все рёбра равны 80. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

71. Площадь основания конуса равна 36. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 17 и 34, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

72. Середина ребра куба со стороной 0,7 является центром шара радиуса 0,35. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответ запишите S/ℼ.

73. Объём параллелепипеда ABCDA₁B₁C₁D₁ равен 4,8. Найдите объём треугольной пирамиды ABCB_1.