ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа разработана на основе авторской программы Е.А.Бунимович«Математика. Рабочие программы. Предметная линия учебников «Сфера» 6 класс»– Москва «Просвещение», 2011 .
В рабочей программе учтены идеи и положения Концепции духовно-нравственного развития и воспитания личности гражданина России. Программы развития и формирования универсальных учебных действий, которые обеспечивают формирование российской гражданской идентичности, овладения ключевыми компетенциями, составляющими основу для саморазвития и непрерывного образования, целостность общекультурного, личностного и познавательного развития учащихся, и коммуникативных качеств личности.
Эта программа является основой для организации работы учителя, ведущего преподавание по указанному учебно-методическому комплекту. В ней цели и требования к результатам обучения математике в основной школе конкретизированы применительно к этапу 6 класс. Программа задаёт содержание и структуру курса, последовательность учебных тем в учебниках линии «Сферы». В ней также приводится характеристика видов учебной и познавательной деятельности, которые служат достижению поставленных целей и обеспечиваются УМК «Сферы».
Цели и задачи курса математики
Продолжение формирования центральных математических понятий (число, величина, геометрическая фигура), обеспечивающих преемственность и перспективность математического образования школьников.
Подведение учащихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, понимание математики как части общей культуры человечества.
Развитие интеллектуальных и творческих способностей учащихся, познавательной активности, критичности мышления, интереса к изучению математики.
Формирование умения извлекать информацию, новое знание, работать с учебным математическим текстом.
Вклад математики в достижение целей основного общего образования
Математическое образование играет важную роль, как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что её предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологически идей. Каждому человеку в своей жизни приходится выполнять расчёты, находить в справочниках нужные формулы и применят), и владеть практическими приёмами геометрических измерении и построений, читать информацию, представленную в виде таблиц диаграмм, графиков, понимать вероятностный характер случайных событий, составлять алгоритмы и др.
В школе математика служит опорным предметом для изучения смежных дисциплин. Всё больше специальностей, где пси, ходим высокий уровень образования, связано с непосредственными применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психологияи др.). Реальной необходимостью в наши дни является
непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической.
В процессе школьной математической деятельности происходит овладение такими мыслительными операциями, как индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, отличиях математического метода от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, входит в интеллектуальный багаж каждого культурного человека.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
Общая характеристика курса математики 6 класса
В Федеральном государственном образовательном стандартеи Примерной программе основного общего образования сформулированы цели обучения математике в основной школе и требования к результатам освоения содержания курса. Эти целевые установки носят общий характер и задают направленность обучения математике в основной школе в целом. В данной рабочей программе они конкретизированы применительно к этапу 5-6 классов с учетом возрастных возможностей учащихся. В качестве приоритетных выдвигаются следующие цели:
подведение учащихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, пониманию математики как части общей культуры человечества;
развитие познавательной активности; формирование мыслительных операций, являющихся основой интеллектуальной деятельности; развитие логического мышления, алгоритмического мышления; формирование умения точно выразить мысль;
развитие интереса к математике, математических способностей;
формирование знаний и умений, необходимых для изучения курсов математики 7-9 классов, смежных дисциплин, применения в повседневной жизни.
В данной рабочей программе курс 6 класса линии УМК «Сферы» представлен как арифметико-геометрический с включением элементов алгебры. Кроме того, к нему отнесено начало изучения вероятностно-статистической линии, а также элементов раздела «Логика и множества», возможность чего предусмотрено Примерной программой по математике для 5 - 9 классов.
Содержание раздела «Арифметика» служит базой для дальнейшего изучения математики и смежных предметов, способствует развитию логического мышления учащихся, формированию умения пользоваться алгоритмами, а также приобретении практических навыков, необходимых в повседневной жизни. При изучении арифметики формирование теоретических знании сочетается с развитием вычислительной культуры, которая актуальна и при наличии вычислительной техники, в частности, г обучением простейшим приёмам прикидки и оценки результата вычислений. Развитие понятия о числе связано с изучением рациональных чисел: натуральных чисел, обыкновенных и десятичных дробей, положительных и отрицательных чисел. Параллельно на доступном для учащихся данного возраста уровне г. курсе представлена научная идея — расширение понятия числа.
В задачи изучения раздела «Геометрия» входит развитие геометрических представлений учащихся, образного мышления, пространственного воображения, изобразительных умений. Этотэтап изучения геометрии осуществляется в 6 классах на наглядно-практическом уровне, при этом большая роль отводится опыту, эксперименту. Учащиеся знакомятся с геометрическими фигурами и базовыми конфигурациями, овладевают некоторыми приёмами построения, открывают их свойства, применяют эти свойства при решении задач конструктивного и вычислительного характера.
Изучение раздела «Алгебра» в основной школе предполагает, прежде всего, овладение формальным аппаратом буквенного исчисления. Это материал более высокого, нежели арифметика уровня абстракции. Его изучение решает целый ряд задач методологического, мировоззренческого, личностного характера, но в то же время требует определенного уровня интеллектуального развития. Поэтому в курсе 6 классов представлены только начальные, базовые алгебраические понятия, и он играет роль своего рода мостика между арифметикой и алгеброй, назначение которого можно образно описать так: от чисел к буквам.
Изучение раздела «Вероятность и статистика» вносит существенный вклад в осознание учащимися прикладного и практического значения математики. В задачи его изучения входит формирование умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, оценивать вероятность наступления события. Основное содержание этого раздела отнесено к 7-9 классам. Для курса 6 классов выделены следующие вопросы: формирование умений работать с информацией, представленной в форме таблиц и диаграмм, первоначальных знаний о приёмах сбора и представления информации, первое знакомство с комбинаторикой, решение комбинаторных задач.
Введение в курс элементарных теоретико-множественных понятий и соответствующей символики способствует обогащению математического языка школьников, формированию умения точно и сжато формулировать математические предложения, помогает обобщению и систематизации знаний.
В содержание основного общего образования, предусмотренного Примерными программами по математике для 5-9 классов, включён также раздел «Математика в историческом развитии». Его элементы представлены и в содержании курса 6 классов. Назначение этого материала состоит в создании гуманитарного, культурно-исторического фона при рассмотрении проблематики основного содержания.
Место математики в учебном плане основной школы
В соответствии с учебным планом основного общего образования в курсе математики выделяются два этапа — 5-6 классы и 7-9 классы, у каждого из которых свои самостоятельные функции. В 5-6 классах изучается интегрированный предмет «Математика», в 7—9 классах — два предмета «Алгебра» и «Геометрия». Курс 5—6 классов, с одной стороны, является непосредственным продолжением курса математики начальной школы, систематизирует, обобщает и развивает полученные там знания, с другой стороны, позволяет учащимся адаптироваться к новому уровню изучения предмета, создает необходимую основу, на которой будут базироваться систематические курсы 7-9 классов.
На изучение математики в основной школе отводится 5 часов в неделю в течение всех лет обучения. Таким образом, на интегрированный курс «Математика» в 6 классах всего отводится 175 уроков.
Личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса;
К важнейшим результатам обучения математике в 6 классах при преподавании по УМК «Сферы» относятся следующие:
• в личностном направлении:
1) знакомство с фактами, иллюстрирующими важные этапы развития математики (изобретение десятичной нумерации, обыкновенных дробей, десятичных дробей; происхождение геометрии из практических потребностей людей);
способность к эмоциональному восприятию математических объектов, рассуждений, решений задач, рассматриваемых проблем;
умение строить речевые конструкции (устные и письменные) с использованием изученной терминологии и символики, понимать смысл поставленной задачи, осуществлять перевод с естественного языка на математический и наоборот;
вметапредметном направлении:
умение планировать свою деятельность при решении учебных математических задач, видеть различные стратегии решения задач, осознанно выбирать способ решения;
умение работать с учебным математическим текстом, находить ответы на поставленные вопросы, выделять смысловые фрагменты и пр.);
умение проводить несложные доказательные рассуждения, опираясь на изученные определения, свойства, признаки, распознавать верные и неверные утверждения; иллюстрировать примерами изученные понятия и факты; опровергать с помощью контрпримеров неверные утверждения;
умение действовать в соответствии с предложенным алгоритмом, составлять несложные алгоритмы вычислений и построений;
применение приёмов самоконтроля при решении учебных задам ,
умение видеть математическую задачу в несложных практических ситуациях;
впредметном направлении:
владение базовым понятийным аппаратом по основным разделам содержания;
владение навыками вычислений с натуральными числа ми, обыкновенными и десятичными дробями, положительными и отрицательными числами;
умение решать текстовые задачи арифметическим способом, используя различные стратегии и способы рассуждения;
усвоение на наглядном уровне знаний о свойствах плоских и пространственных фигур; приобретение навыков их изображения; умение использовать геометрический язык для описания предметов окружающего мира;
приобретение опыта измерения длин отрезков, величин углов, вычисления площадей и объёмов; понимание идеи измерения длин, площадей, объёмов;
знакомство с идеями равенства фигур, симметрии; умение распознавать и изображать равные и симметричные фигуры;
умение проводить несложные практические расчеты (включающие вычисления с процентами, выполнение необходимых измерений, использование прикидки и оценки);
использование букв для записи общих утверждений, фор мул, выражений, уравнений; умение оперировать понятием «буквенное выражение», осуществлять элементарную деятельность, связанную с понятием «уравнение»;
знакомство с идеей координат на прямой и на плоскости выполнение стандартных процедур на координатной плоскости:
понимание и использование информации, представленной в форме таблицы, столбчатой или круговой диаграммы;
умение решать простейшие комбинаторные задачи перебором возможных вариантов.
СОДЕРЖАНИЕ КУРСА МАТЕМАТИКИ 6 КЛАССА
Арифметика
Натуральные числа. Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий.
Степень с натуральным показателем.
Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическим способом.
Делители и кратные. Свойства и признаки делимости. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком.
Дроби. Обыкновенная дробь. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части.
Десятичная дробь. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.
Проценты; нахождение процента от величины и величины по ее проценту. Отношение; выражение отношения в процентах.
Решение текстовых задач арифметическим способом.
Рациональные числа. Положительные и отрицательные числа, модуль числа. Множество целых чисел. Множестворациональных чисел; рациональное число как отношение 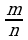 ,где т — целое число,п — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.
,где т — целое число,п — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.
Координатная прямая; изображение чисел точками координатной прямой.
Измерения, приближения, оценки. Единицы измерения длины, площади, объёма, массы, времени, скорости. Приближённое значение величины. Округление натуральных чисел и десятичных дробей. Прикидка и оценка результатов вычислений.
Элементы алгебры
Использование букв для обозначения чисел, для записи свойств арифметических действий. Буквенные выражения. Числовое значение буквенного выражения. Допустимые значения букв в выражении.
неизвестных компонентов арифметических действий. Примеры решения текстовых задач с помощью уравнений.
Декартовы координаты на плоскости. Построение точки по координатам, определение координат точки на плоскости.
Описательная статистика. Комбинаторика
Представление данных в виде таблиц, диаграмм.
Решение комбинаторных задач перебором вариантов.
Наглядная геометрия
Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг,четырёхугольник, прямоугольник, квадрат. Треугольник, видь треугольников. Правильные многоугольники. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности.
Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины.
Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Биссектриса угла.
Понятие площади фигуры; единицы измерения площади Площадь прямоугольника, квадрата. Приближённое измерение площади фигур на клетчатой бумаге. Равновеликие фигуры.
Наглядные представления о пространственных фигурах: куб параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примерь развёрток многогранников, цилиндра и конуса.
Понятие объёма; единицы объёма. Объём прямоугольного параллелепипеда, куба.
Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.
Логика и множества
Множество, элемент множества. Задание множества перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначения. Подмножество. Объединение и пересечение множеств.
Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна.Пример и контрпример.
6 класс (175 ч)
Дроби и проценты (20 ч)
Повторение: понятие дроби, основное свойство дроби, сравнение и упорядочивание дробей, правила выполнения арифметических действий с дробями. Преобразование выражений с помощью основного свойства дроби. Решение основных задач на дроби. Понятие процента. Нахождение процента от величины. Столбчатые диаграммы: чтение и построение. Круговые диаграммы.
Основные цели - систематизировать знания об обыкновенных дробях, закрепить и развить навыки действий с обыкновенными дробями, познакомить учащихся с понятием процента, а также развить умение работать с диаграммами.
Прямые на плоскости и в пространстве (7 ч)
Пересекающиеся прямые. Вертикальные углы, их свойство. Параллельные прямые. Построение параллельных и перпендикулярных прямых. Примеры параллельных и перпендикулярных прямых в окружающем мире. Расстояние между двумя точками, от точки до прямой, между двумя параллельными прямыми, от точки до плоскости.
Основные цели - создать у учащихся зрительные образы всех основных конфигураций, связанных с взаимным расположением двух прямых на плоскости и в пространстве, сформировать навыки построения параллельных и перпендикулярных прямых, научить находить расстояние от точки до прямой, между двумя параллельными прямыми.
Десятичные дроби (10 ч)
Десятичная запись дробей. Представление обыкновенной дроби в виде десятичной и десятичной в виде обыкновенной; критерий обратимости обыкновенной дроби в десятичную. Изображение десятичных дробей точками на координатной прямой. Сравнение десятичных дробей. Десятичные дроби и метрическая система мер.
Основные цели - ввести понятие десятичной дроби, выработать навыки чтения записи десятичных дробей, их сравнения; сформировать умения переходить от десятичной дроби к обыкновенной, выполнять обратные преобразования.
Действия с десятичными дробями (27 ч)
Сложение и вычитание десятичных дробей. Умножение и деление десятичной дроби на 10. Умножение и деление десятичных дробей. Округление десятичных дробей. Приближенное частное. Выполнение действий с обыкновенными и десятичными дробями.
Основная цель - сформировать навыки действий с десятичными дробями, а также навыки округления десятичных дробей.
Окружность (9 ч)
Взаимное расположение прямой и окружности, двух окружностей. Касательная к окружности и ее построение. Построение треугольника по трем сторонам. Неравенство треугольника. Круглые тела.
Основные цели - создать у учащихся зрительные образы основных конфигураций, связанных с взаимным расположением прямой и окружности, двух окружностей на плоскости; научить строить треугольник по трем сторонам, сформировать представление о круглых телах (шар, конус, цилиндр).
Отношения и проценты (17 ч)
Отношение чисел и величин. Масштаб. Деление в данном отношении.
Выражение процентов десятичными дробями; решение задач на проценты. Выражение отношения величин в процентах.
Основные цели - познакомить с понятием "отношение" и сформировать навыки использования соответствующей терминологии; развить навыки вычисления с процентами.
Выражения, формулы, уравнения (15 ч)
Применение букв для записи математических выражений и предложений. Буквенные выражения и числовые подстановки. Формулы. Формулы периметра треугольника, периметра и площади прямоугольника, объема параллелепипеда. Формулы длины окружности и площади круга.
Уравнение. Корень уравнения. Составление уравнения по условию текстовой задачи.
Основные цели - сформировать первоначальные представления о языке математики, описать с помощью формул некоторые известные учащимся зависимости, познакомить с формулами длины окружности и площади круга.
Симметрия (8 ч)
Осевая симметрия. Ось симметрии фигуры. Центральная симметрия. Построение фигуры, симметричной данной относительно прямой и относительно точки. Симметрия в окружающем мире.
Основные цели - познакомить учащихся с основными видами симметрии на плоскости; научить строить фигуру, симметричную данной фигуре относительно прямой, а также точку, симметричную данной относительно точки; дать представление о симметрии в окружающем мире.
Целые числа (15 ч)
Числа, противоположные натуральным. "Ряд" целых чисел. Изображение целых чисел точками на координатной прямой. Сравнение целых чисел. Сложение и вычитание целых чисел; выполнимость операции вычитания. Умножение и деление целых чисел; правила знаков.
Основные цели - мотивировать введение отрицательных чисел; сформировать умение сравнивать целые числа с опорой на координатную прямую, а также выполнять действия с целыми числами.
Рациональные числа (17 ч)
Отрицательные дробные числа. Понятие рационального числа. Изображение чисел точками на координатной прямой. Противоположные числа. Модуль числа, геометрическая интерпретация модуля. Сравнение рациональных чисел. Арифметические действия с рациональными числами, свойства арифметических действий.
Примеры использования координат в реальной практике. Прямоугольная система координат на плоскости. Координаты точки на плоскости, абсцисса и ордината. Построение точек и фигур на координатной плоскости.
Основные цели - выработать навыки действий с положительными и отрицательными числами; сформировать представление о декартовой системе координат на плоскости.
Многоугольники и многогранники (10 ч)
Сумма углов треугольника. Параллелограмм и его свойства, построение параллелограмма. Правильные многоугольники. Площади, равновеликие и равносоставленные фигуры. Призма.
Основные цели - развить знания о многоугольниках; развить представление о площадях, познакомить со свойством аддитивности площади, с идеей перекраивания фигуры с целью определения ее площади; сформировать представление о призме; обобщить приобретенные геометрические знания и умения и научить применять их при изучении новых фигур и их свойств.
Множества. Комбинаторика. (9 ч)
Понятие множества. Примеры конечных и бесконечных множеств. Подмножества. Основные числовые множества и соотношения между ними. Разбиение множества. Объединение и пересечение множеств. Иллюстрация отношений между множествами с помощью кругов Эйлера.
Решение комбинаторных задач перебором всех возможных вариантов.
Случайное событие. Достоверное и невозможное события. Сравнение шансов событий.
Основные цели - познакомить с простейшими теоретико-множественными понятиями, а также сформировать первоначальные навыки использования теоретико-множественного языка; развить навыки решения комбинаторных задач путем перебора всех возможных вариантов.
13. Повторениекурса (11 ч)
Тематическое планирование 6 класс 175 часов
| № п\п | Разделы, темы | Количество часов |
| Авторская программа | Рабочая программа |
| 1. | Количество тем | 13 | 13 |
| 2. | Объем часов на прохождение всех тем | 175 | 175 |
| 3. | Объем часов на прохождение каждой темы |
|
|
| 3.1 | Дроби и проценты | 22 | 22 |
| 3.2 | Прямые на плоскости и в пространстве | 7 | 7 |
| 3.3 | Десятичные дроби | 9 | 9 |
| 3.4 | Действия с десятичными дробями | 28 | 28 |
| 3.5 | Окружность | 9 | 9 |
| 3.6 | Отношения и проценты | 17 | 17 |
| 3.7 | Выражения, формулы, уравнения | 15 | 15 |
| 3.8 | Симметрия | 9 | 9 |
| 3.9 | Целые числа | 13 | 13 |
| 3.10 | Рациональные числа | 17 | 17 |
| 3.11 | Многоугольники и многогранники | 10 | 10 |
| 3.12 | Множества. Комбинаторика. | 8 | 8 |
| 3.13 | Повторение курса | 11 | 11 |
| 4. | Контрольные работы | 13 | 13 |
Перечень контрольных работ. 6 класс
Контрольная работа №1 по теме «Дроби и проценты»
Контрольная работа № 2 по теме «Прямые на плоскости и в пространстве»
Контрольная работа №3 по теме «Десятичные дроби»
Контрольная работа №4 по теме «Действия с десятичными дробями»
Контрольная работа № 5 по теме «Окружность»
Контрольная работа №6 по теме «Отношения и проценты»
Контрольная работа №7 по теме «Выражения, формулы, уравнения»
Контрольная работа №8 по теме «Симметрия»
Контрольная работа №9 по теме «Целые числа»
Контрольная работа №10 по теме «Рациональные числа»
Контрольная работа № 11 по теме «Многоугольники и многогранники»
Контрольная работа № 12 по теме «Множества. Комбинаторика»
Контрольная работа № 13 по теме «Повторение к
6 класс
1.Бунимович Е.А. Математика. Арифметика. Геометрия. 6 класс: учебник для общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др. — М.: Просвещение, 2010.
2.Электронное приложение к учебнику. — М. : Просвещение, 2011.
3. Бунимович Е.А. Математика. Арифметика. Геометрия. Тетрадь-тренажёр. 6 класс: пособие для учащихся общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др. — М. : Просвещение, 2010.
4. Бунимович Е.А. Математика. Арифметика. Геометрия. Задачник. 6 класс: пособие для учащихся общеобразоват. учреждений. / Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и Ф. — М. : Просвещение, 2010.
5. Кузнецова Л.В. Математика. Арифметика. Геометрия. Тетрадь - экзаменатор. 6 класс: пособие для учащихся общеобразоват. учреждений. / Л.В. Кузнецова, С.С. Минаева, Л.С. и др. М. : Просвещение, 2010.
6. Кузнецова Л.В. Математика. Поурочное тематическое планирование 6 класс: пособие для учителей общеобразоват. учреждений. / Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова и др М. : Просвещение, 2011
Оснащение процесса обучения математике обеспечивается библиотечным фондом, печатными пособиями, а также информационно-коммуникативными средствами, экранно-звуковыми пособиями, техническими средствами обучения, учебно-практическим и учебно-лабораторным оборудованием.
коллекция медиаресурсов, электронные базы данных;
Интернет.Гиперссылки на ресурс:http://eorhelp.ru/
http://www.fcior.edu.ru
http://www.school-collection.edu.ru
http://www.openclass.ru/
http://powerpoint.net.ru/
http://karmanform.ucoz.ru/
доска магнитная с координатной сеткой;
комплект чертежных инструментов (классных и раздаточных): линейка, транспортир, угольник (30°, 60°), угольник (45°, 45°), циркуль;
комплекты планиметрических и стереометрических тел (демонстрационный и раздаточный);
комплекты для моделирования (цветная бумага, картон, калька, клей, ножницы, пластилин).
таблицы по математике для 5 -6 классов;
портреты выдающихся деятелей математики.
Сайт интернет-поддержки УМК «Сферы»: www.sрhегеs.ги
Планируемые результаты изучения учебного предмета, курса.
В результате изучения математики ученик будет
знать/понимать
в личностном направлении:
1) знакомство с фактами, иллюстрирующими важные этапы развития математики (изобретение десятичной нумерации, обыкновенных дробей, десятичных дробей; происхождение геометрии из практических потребностей людей);
способность к эмоциональному восприятию математических объектов, рассуждений, решений задач, рассматриваемых проблем;
умение строить речевые конструкции (устные и письменные) с использованием изученной терминологии и символики, понимать смысл поставленной задачи, осуществлять перевод с естественного языка на математический и наоборот;
вметапредметном направлении:
особенности десятичной системы счисления;
названия рядов и классов;
термины «приближённое значение с недостатком», «приближённое значение с избытком»; «степень числа», «основание степени», «показатель степени»
как связаны между собой действия сложения и вычитания, умножения и деления;
переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения относительно сложения;
что такое «делитель», «кратное», взаимосвязь между ними;
обозначения НОД(а;в) и НОК (а;в);
определение простого числа;
признаки делимости на 2, на 5, на 10, на 3 и на 9;
что означают знаменатель и числитель дроби;
правила сложения, вычитания, умножения и деления дробей с одинаковыми и разными знаменателями;
уметь в предметном направлении:
различать виды линий и углов;
проводить и обозначать прямую, луч, отрезок, ломаную;
строить отрезок заданной длины, угол заданной величины, биссектрису угла; равнобедренный треугольник по боковым сторонам и углу между ними, прямоугольник на нелинованной бумаге с помощью чертёжных инструментов; находить длину отрезка и величину угла;
распознавать окружность, многоугольники, цилиндр, конус, шар, многогранники; проводить окружность заданного радиуса; изображать многоугольники с заданными свойствами, вычислять периметр многоугольника;
переходить от одних единиц измерения к другим единицам, выбирать подходящие единицы измерения в зависимости от контекста задачи;
представлять натуральное число в виде суммы разрядных слагаемых:
читать и записывать натуральные числа, а также числа, записанные римскими цифрами;
сравнивать и упорядочивать натуральные числа и дроби; читать и записывать двойные неравенства;
изображать натуральные числа на координатной прямой;
округлять натуральные числа до указанного разряда, поясняя при этом свои действия;
выполнять арифметические действия с натуральными числами, находить значения числовых выражений, устанавливая порядок выполнения действий;
находить неизвестное число в равенстве на основе зависимости между компонентами действий;
возводить натуральное число в натуральную степень;
решать несложные текстовые задачи арифметическим методом; решать несложные арифметические задачи на движение; на части и уравнивание;
представлять произведение нескольких равных множителей в виде степени с натуральным показателем;
использовать свойства сложения и умножения для преобразования числовых выражений;
находить НОК и НОД;
находить дробь от величины;
соотносить дроби и точки на координатной плоскости;
сокращать дроби, приводить к новому знаменателю, к общему знаменателю;
выделять целую часть из неправильной дроби и представлять смешанное число в виде неправильной дроби;
анализировать готовые таблицы и диаграммы;
заполнять несложные таблицы, следуя инструкции.
| раздел | Планируемые результаты |
| личностные | метапредметные | предметные |
| Арифметика | Ученик получит возможность: Ответственно относится к учебе, Грамотно излагать свои мысли Критично мыслить, быть инициативным, находчивым, активным при решении математических задач. | Ученик научится: Действовать по алгоритму, Видеть математическую задачу в окружающей жизни. Представлять информацию в различных моделях Ученик получит возможность:
Устанавливать причинно-следственные связи. Строить логические рассуждения, Умозаключения и делать выводы Развить компетентность в области использования информационно- коммуникативных технологий. | Ученик научится: •понимать особенности десятичной системы счисления; Формулировать и применять при вычислениях свойства действия над рациональными( неотриц.) числами4 Решать текстовые задачи с рациональными числами; Выражать свои мысли с использованием математического языка. Ученик получит возможность: Углубить и развить представления о натуральных числах; Использовать приемы рационализирующие вычисления и решение задач с рациональными(неотр) числами. |
| Элементы алгебры. | Ученик получит возможность: Ответственно относится к учебе. Грамотно излагать свои мысли Контролировать процесс и результат учебной деятельности Освоить национальные ценности, традиции и культуру родного края используя краеведческий материал. | Ученик научится: Действовать по алгоритму; видеть математическую задачу в различных формах. Ученик получит возможность: Выделять альтернативные способы достижения цели и выбирать эффективные способы решения. | Ученик научится: Читать и записывать буквенные выражения, составлять буквенные выражения. Составлять уравнения по условию. Решать простейшие уравнения. Ученик получит возможность: Развить представления о буквенных выражениях Овладеть специальными приемами решения уравнений, как текстовых, так и практических задач. |
| Описательная статистика. Комбинаторные задачи | Ученик получит возможность :ответственно относится к учебе, контролировать процесс и результат учебной и математической деятельности. Критично мыслить, быть инициативным, находчивым, активным при решении комбинаторных задач. | Ученик научится: Представлять информацию в различных моделях. Ученик получит возможность: Выделять альтернативные способы достижения цели и выбирать эффективные способы решения | Ученик научится: Решать комбинаторные задачи с помощью перебора вариантов.
Ученик получит возможность: Приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения; Осуществлять их анализ, представлять результаты опроса в виде таблицы. •научится некоторым приемам решения комбинаторных задач. |
| Наглядная геометрия | Ученик получит возможность :ответственно относится к учебе, контролировать процесс и результат учебной и математической деятельности. Критично мыслить, быть инициативным, находчивым, активным при решении геометрических задач. | Ученик научится: действовать по алгоритму, видеть геометрическую задачу в окружающей жизни, представлять информацию в различных моделях. Ученик получит возможность: Извлекать необходимую информацию, анализировать ее, точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования.
| Ученик научится:изображать фигуры на плоскости; • использовать геометрический «язык» для описания предметов окружающего мира; • измерять длины отрезков, величины углов, вычислять площади и объёмы фигур; • распознавать и изображать равные и симметричные фигуры; • проводить не сложные практические вычисления.
Ученик получит возможность: углубить и развить представления о геометрических фигурах. |
| Логика имножества | Ученик получит возможность :ответственно относится к учебе, контролировать процесс и результат учебной и математической деятельности. Обсуждать соотношение между основными числовыми множествами. Записывать на символическом языке соотношения между множествами и приводить примеры различных вариантов их перевода на русский язык | Ученик научится: . Исследовать вопрос о числе подмножеств конечного множества Ученик получит возможность :Проводитьлогические рассуждения по сюжетам текстовых задач с помощью кругов Эйлера. Приводить примеры классификаций из математики и из других областей знания | Ученик научится: Формулировать определения объединения и пересечения множеств. Иллюстрировать эти понятия с помощью кругов Эйлера.
Ученик получит возможность : Использовать схемы в качестве наглядной основы для разбиения множества на непересекающиеся подмножества. |
Критерии и нормы оценки знаний, умений и навыков учащихся.
Оценка письменных контрольных работ обучающихся по математике
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.







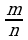 ,где т — целое число,п — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.
,где т — целое число,п — натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.









