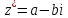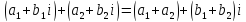Тема: Понятие комплексного числа. Действия с комплексными числами в алгебраической форме.
Цели:
Образовательные: расширить понятие числа, ввести понятие комплексного числа, действия над комплексными числами, заданными в алгебраической форме.
Воспитательные: прививать интерес к математике, ознакомить обучающихся с историей развития комплексных чисел.
Развивающие: развивать творческое мышление, пространственное мышление, научить применять теоретические знания при решении практических задач, формировать активность и самостоятельность при работе в группах.
Вид занятия: усвоение новых знаний.
План занятия:
Организационный момент.
Изучение нового материала.
Закрепление нового материала.
Контроль и самопроверка знаний.
Рефлексия.
Домашнее задание.
Ход занятия:
Организационный момент.
Приветствие студентов, перекличка и отметка отсутствующих в журнале.
Изучение нового материала.
После того как мы определили тему занятия, давайте послушаем краткую историю возникновения комплексных чисел. Выступает студент с сообщением (Приложение 1, примерный текст сообщения). Остальные делают записи в тетрадях.
После того как все прослушали сообщение выступающего, предлагается ответить на вопросы:
В каком веке появилась необходимость извлечение квадратного корня из отрицательного числа?
Кто ввел в обиход понятие «мнимые» числа?
Кто изменил название «мнимые числа» на «комплексные»?
Запишем в тетрадях:
Определение: комплексными числами называются числа вида 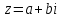 , где а и b- действительные числа, а число i, определяемое равенством i² = –1, называется мнимой единицей.
, где а и b- действительные числа, а число i, определяемое равенством i² = –1, называется мнимой единицей.
Запись комплексного числа в виде 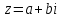 , называется алгебраической формой записи комплексного числа.
, называется алгебраической формой записи комплексного числа.
Определение: комплексное число  называется комплексно-сопряженным с числом
называется комплексно-сопряженным с числом 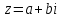 и обозначается
и обозначается 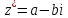
Определение: Модулем комплексного числа 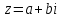 , называется число
, называется число 
Правило сложения:
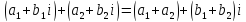
Решим пример
(3+5i)+(6+3i)=9+8i
Правило вычитания:

Решим пример
(4+2i)–(1+5i)=3–3i
Правило умножения:

Решим пример
(2+5i)·(4+2i)=8+4i+20i+10i²=8+24i–10=–2+24i
Правило деления:

Решим пример

Закрепление нового материала.
Тренировочные упражнения №1 (Приложение 2).
Выполняется у доски, желающие делают самостоятельно на оценку, в конце пары сдаются тетради на проверку.
Контроль и самопроверка знаний.
Самостоятельная работа
Раздаются карточки с заданиями для самостоятельной работы.
6 вариантов (Приложение 3)
Рефлексия.
О каком множестве чисел вы сегодня узнали?
Кто ввел понятие «комплексные числа»?
Можно ли вычислить корень из отрицательного числа?
Домашнее задание.
Найти модуль комплексного числа: 
Решить уравнение: 
Выполнить деление: 
Приложение 1.
Примерное сообщение студента
История развития числа уходит корнями в древние времена. В VIII в. Ученые знали, что у положительного числа существует два квадратных корня: один –положительное число, другой – отрицательное, но считали, что из отрицательных чисел нельзя извлекать квадратный корень.
В XVI в. В связи с изучением решений кубических уравнений возникла необходимость извлечения квадратных корней из отрицательных чисел. В 1545 г. итальянский математик Дж. Кардано (1501-1576) опубликовал работу «Великое искусство», в которой привел формулу корней кубического уравнения, для которой понадобились числа новой природы, которые он назвал «чисто отрицательными» или «софистически отрицательными» и считал их бесполезными.
Однако, уже в 1572 г. в книге другого итальянского математика Р. Бомбелли (1530-1572) были изложены правила арифметических действий над комплексными числами в том виде, в каком они известны и нам. В те времена комплексные числа называли мнимыми. Такое название ввел в обиход Р.Декарт, а обозначать буквой i предложил в 1777 г. Л.Эйлер. В математической литературе символ i широко стал использоваться после публикации в 1831 г. работы немецкого математика К. Гаусса (1777-1855) «Теория биквадратных остатков». В этой работе Гаусс заменил название «мнимых чисел» на комплексные и окончательно закрепил для науки геометрическую интерпретацию комплексного числа как точки координатной плоскости. Позднее комплексные числа также стали изображать с помощью векторов на координатной плоскости.
Так же значительный вклад в развитие теории функций комплексной переменной внести видные отечественные математики М.В. Келдыш, М.А. Лаврентьев, Н.Н. Боголюбов и др.
Приложение 2.
Тренировочные упражнения
Найти действительные числа х и у, если:
6х+3уi=4+2i
х-3уi=-5- i
i
х-(4-у)i=- i
i
х-(х+у)i=3+2i
(х+у)+(х-у)i=8+2i
Найти сумму комплексных чисел:
(1+i)+(-1-i)


( -2i)+(
-2i)+( )
)
(-4+3i)+(4-3i)
Найти произведение комплексных чисел:
(-5+ i)(-6-3
i)(-6-3 )
)
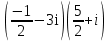

(5-3i)(2-5i)
(4+7i)(2-i)
Найти разность комплексных чисел:
1)
2) ( )-(2
)-(2 )
)
3) (7+2i)-(3+2i)
4) (4+i)-(-5+i)
5) (4+3i)-(4-3 )
)
5. Найти частное двух комплексных чисел:
1) 
2) 
3) 
4) 
5) 
6. Найти модуль и главное значение аргумента:
1) z=i 2) z=-5i 3) z=-1+i 4) z=2-2i 5) z=3 6) z=-3 7) z=3i 8) z=-3i
9) z=-2-2i 10) z=1+ i 11) z=1-
i 11) z=1- i 12) z=
i 12) z= i 13) z=-1+i
i 13) z=-1+i
14) z= i
i
7. Решить уравнение:
1) (2+3i)+z=-4+i 2) (-1+2i)+z=5 - i
i
3)  4) 6-i=z+(5-
4) 6-i=z+(5- )i
)i
Приложение 3.
Самостоятельная работа
Вариант № 1
Даны комплексные числа:  .
.
Вычислить: а)  , б)
, б) , в)
, в) , г)
, г)  , д)
, д) , е)
, е)
Упростить выражение:
(a+2bi)+(a-3bi)
(2a+3bi)(2a-3bi)
Найти частное комплексных чисел:


Вариант № 2
Даны комплексные числа:  .
.
Вычислить: а)  , б)
, б) , в)
, в) , г)
, г)  , д)
, д) , е)
, е)
Упростить выражение:
(4a+5bi)+(-3a-5bi)
(2a+3bi)(3b+2ai)
Найти частное комплексных чисел:

Вариант № 3
Даны комплексные числа:  .
.
Вычислить: а)  , б)
, б) , в)
, в) , г)
, г)  , д)
, д) , е)
, е)
Упростить выражение:
(a+5bi) (-3a-bi)
(4a+3bi)(5b+ai)
Найти частное комплексных чисел:
-

Вариант № 4
Даны комплексные числа: .
Вычислить: а)  , б)
, б) , в)
, в) , г)
, г)  , д)
, д) , е)
, е)
Упростить выражение:
(4-3i)-(1+2i)(2-3i)
(1+i)(2-3i)
Найти частное комплексных чисел:


Вариант № 5
Даны комплексные числа:  .
.
Вычислить: а)  , б)
, б) , в)
, в) , г)
, г)  , д)
, д) , е)
, е)
Упростить выражение:
(1-2i)- (5+7i)(2-i)
(-4+2i)(5+i)
Найти частное комплексных чисел:


Вариант № 6
Даны комплексные числа:  .
.
Вычислить: а)  , б)
, б) , в)
, в) , г)
, г)  , д)
, д) , е)
, е)
Упростить выражение:
(2-i)(2+i)-(3-2i)+7
(1+5i)(2-i)
Найти частное комплексных чисел:









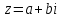 , где а и b- действительные числа, а число i, определяемое равенством i² = –1, называется мнимой единицей.
, где а и b- действительные числа, а число i, определяемое равенством i² = –1, называется мнимой единицей. называется комплексно-сопряженным с числом
называется комплексно-сопряженным с числом