МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ВЫСОТИНСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»
Тема: « Построение многоугольников циркулем и линейкой»
Выполнила : ученица 7 класса
Федосенко Кристина
Руководитель: Сергеева Наталья Владимировна
Учитель математики
ВЫСОТИНО 2014
Содержание
| Название раздела | Страница |
Введение
| 3 |
Простейшие построения
| 3 |
Построение отрезка, равного данному
| 3 |
Построение угла равного данному
| 3 |
Построение биссиктрисы угла
| 4 |
Построение перпендикулярной прямой через точку, лежащую на прямой
| 4 |
Построение середины отрезка
| 4 |
Построение перпендикулярной прямой через точку, не лежащую на прямой
| 4 |
Многоугольники (определение , виды)
| 5 |
Построение произвольных многоугольников
| 6 |
Построение правильных многоугольников
| 8 |
Вывод
| 10 |
Литература | 11 |
Приложения |
|
Объект исследования: задачи на построения
Предмет исследования: построения многоугольников
Проблема: Можно ли построить многоугольники с помощью циркуля и линейки
Гипотеза: любой многоугольник можно построить с помощью циркуля и немасштабной линейки.
Введение
В геометрии мы имеем дело с геометрическими построениями: построение прямой, откладывание отрезка определенной длины, построение угла, построение треугольников и других фигур, но при этом пользуемся масштабной линейкой, циркулем, транспортиром, чертежным угольником. В задачах на построение циркуль и линейка считаются идеальными инструментами, в частности:
Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
Циркуль может иметь сколь угодно большой или сколь угодно малый раствор (то есть может чертить окружность произвольного радиуса).
С помощью линейки можно провести прямую и построить прямую, проходящую через две точки. С помощью циркуля можно провести окружность произвольного радиуса с центром в данной точке и радиусом, равным данному отрезку. Выполняя эти несложные операции, можно решить много интересных задач на построения.
Цель моей работы: исследовать построение многоугольников с помощью циркуля и линейки
Для достижения своей цели я ставлю перед собой следующие задачи:
Определить простейшие построения.
Рассмотреть виды многоугольников.
Рассмотреть построение произвольных многоугольников.
Рассмотреть построение правильных многоугольников.
Сделать вывод.
Простейшие построения.
Построение отрезка, равного данному.
Задача: На данном луче от его начала отложить отрезок, равный данному.
Дано: отрезок АВ, луч ОС
Построить: ОД=АВ
Построение:
| Алгоритм построения |
Построить окружность радиуса АВ с центром в точке О. Точка Д – точка пересечения окружности и луча. ОД – искомый отрезок |
Построение: Приложение 1
Построение угла, равного данному.
Задача: Отложить от данного луча угол, равный данному.
Дано: угол с вершиной А, луч ОМ
Построить: угол ЕОД так, чтобы луч ОД и ОМ совпали
Построение:
| Алгоритм построения |
Построить окружность произвольного радиуса с центром в вершине А данного угла. Точки В и С – точки пересечения окружности и сторон угла А. Проведем окружность того же радиуса с центром в точке О. Точка Д – точка пересечения окружности и луча ОМ. Построить окружность радиуса ВС с центром в точке Д. Точка Е – точка пересечения окружностей с центрами О и Д. Угол МОЕ – искомый угол |
Построение: Приложение 2
Построение биссектрисы угла.
Задача: Построить биссектрису данного угла.
Дано: угол с вершиной ВАС
Построить: АЕ – биссектрису угла ВАС
Построение:
| Алгоритм построения |
Построить окружность произвольного радиуса с центром в вершине А данного угла. Точки В и С – точки пересечения окружности и сторон угла А. Проведем окружность радиуса ВС с центром в точке В. Проведем окружность радиуса ВС с центром в точке С. Точки Е и М – точки пересечения окружностей. Е- лежит внутри угла ВАС. АЕ – биссектриса угла |
Построение: Приложение 3
Построение перпендикулярной прямой через точку, лежащую на прямой
Задача: даны прямая а и точка М на прямой. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.
Дано: прямая а, точка М, принадлежащая прямой.
Построить: РМ ┴а
Построение:
| Алгоритм построения |
Построить на лучах прямой а отрезки МА=МВ Проведем окружность радиуса АВ с центром в точке В. Проведем окружность радиуса АВ с центром в точке А. Точки Р и Q – точки пересечения окружностей. Проведем прямую PМ – искомая прямая |
Построение: Приложение 4
Построение середины отрезка
Задача: построить середину данного отрезка
Дано: отрезок АВ
Построить: О – середина отрезка
Построение:
| Алгоритм построения |
Проведем окружность радиуса АВ с центром в точке В. Проведем окружность радиуса АВ с центром в точке А. Точки Р и Q – точки пересечения окружностей. Проведем прямую PQ . О – точка пересечения отрезка АВ и прямой PQ. О – середина отрезка АВ |
Построение: Приложение 5
Построение перпендикулярной прямой через точку, не лежащую на прямой
Задача: даны прямая а и точка М не лежит на прямой. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.
Дано: прямая а, точка М, не принадлежащая прямой.
Построить: РМ ┴а
Построение:
| Алгоритм построения |
Проведем окружность с центром в точке М и пересекающую прямую в двух точках А и В. Проведем окружность радиуса ВМ с центром в точке В. Проведем окружность радиуса АМ с центром в точке А. Точки Р и М – точки пересечения окружностей. Проведем прямую PМ – искомая прямая |
Построение: Приложение 6
Многоугольники.
Многоугольник - фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имею общих точек.
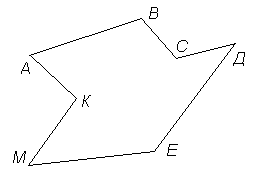
АВСДЕМК – многоугольник; А, В, С, Д, Е, М, К – вершины многоугольника; отрезки АВ, ВС, СД, ДЕ, ЕМ, МК, КА – стороны многоугольника.
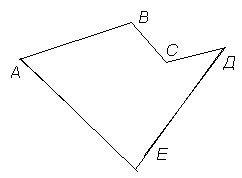
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его вершины.
| Выпуклый многоугольник | Не выпуклый многоугольник |
|
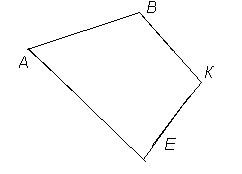
| 
|
Построение произвольных многоугольников.
Многоугольник, у которого все стороны равны, называется правильным.
Я сначала рассмотрю построение произвольных многоугольников, а затем правильных.
| Треугольник | Четырехугольник | Пятиугольник | Шестиугольник | n- угольник |
Произвольный треугольник Поставить три точки, не лежащие на одной прямой Соединить точки последовательно Построение: Приложение7 | Произвольный четырехугольник Построение: Приложение10 | Произвольный пятиугольник
Построение: Приложение13 |
Построение: Приложение 14 |
|
Прямоугольный треугольник Построение: Приложение8 | 2.Четырехугольник с прямым углом построить прямой угол О построить точку К построить отрезок О М на стороне прямого угла, построить ОС на другой стороне прямого угла соединить точку К с точками С и М, О С К М искомый
Построение: Приложение 11 |
| 3.Равнобедренный треугольник построить отрезок А В построить окружность с центром в точке А, любого радиуса построить окружность того же радиуса с центром в точке В одну из точек (М) пересечения окружностей соединить с точками А и В, треугольник АМВ – искомый. Построение: Приложение 9
| 3.Прямоугольник
угол О прямой ОС, ОМ на сторонах угла Угол С прямой, угол М прямой К точка пересечения сторон угла С и угла М
Построение: Приложение12 |
| Вывод: С помощью циркуля и линейки можно построить : произвольный и равнобедренный , прямоугольный треугольники; четырех- ,пяти- и многоугольники |
Построение правильных многоугольников.
Многоугольник, у которого все стороны равны, называется правильным.
| Треугольник | Четырехугольник |
| Правильный треугольник (равносторонний) – все стороны равны
Построить произвольный отрезок АВ построить окружность с центром в точке А, радиуса АВ построить окружность радиуса АВ с центром в точке В одну из точек (М) пересечения окружностей соединить с точками А и В, треугольник АМВ – искомый.
Построение: Приложение 15 | Квадрат угол О прямой ОС = ОМ на сторонах угла Угол С прямой, угол М прямой К точка пересечения сторон угла С и угла М
Построение: Приложение16 |
|
| Ромб
Построить произвольный отрезок АВ построить окружность с центром в точке А, любого радиуса построить окружность того же радиуса с центром в точке В (М), (К)-точки пересечения окружностей, соединить их с точками А и В, полученный четырехугольник АМВК – ромб Построение: Приложение 17 |
Построить правильный шестиугольник, сторона которого равна данному отрезку. АВ – данный отрезок( материал учебника « Геометрия 7- 9», Л.С.Атанасян.)
Построить окружность радиуса АВ.
Отметить на окружности произвольную точку К1.
Не меняя раствор циркуля , построим точки К2, К3, К4, К5, К6 на этой окружности так, чтобы К1К2=К2К3=К3К4=К4К5=К5К6.
Соединим последовательно эти точки.
К1К2К3К4К5К6 – искомый шестиугольник
Приложение 18
А1А2А3..... Аn
построим биссектрисы двух смежных углов
О — точка пересечения биссектрис
построим окружность с центром в точке О , радиусом ОА1
построим серединные перпендекуляры к сторонам n угольника
В1В2...Вn – точки пересечения серединных перпендекуляров и окружности
А1В1 А2В2... - искомый 2n- угольник
Приложение 19
Мы рассмотрели построение многоугольников с четным числом сторон.
Как построить правильный многоугольник с произвольным числом сторон?
Алгоритм построения правильных многоугольников, с помощью с циркуля и линейки.
Задача построения правильного n – угольника сводиться к делению окружности на n равных частей. Один практический приём такого деления предложил французский математик Н. Бион.
Приём состоит в следующем: пусть требуется разделить окружность, например, на 9 равных частей.
На диаметре окружности строится равносторонний треугольник АВС. Диаметр АВ делим на 9 равных частей.
Проведём луч из точки А и отложим на нём с помощью циркуля 9 равных отрезков.
Соединим конец девятого отрезка с точкой В.
Далее через точки проведём параллельные отрезки.
Соединяя вторую точку деления с вершиной треугольника С, продолжим прямую до пересечения с окружностью в точке Д.
Дуга АД является девятой частью окружности, хорда АД – стороной правильного девятиугольника.
Проверим, можно ли с помощью этого приёма разделить окружность на любое число n –равных частей, как на чётное число n, так и на нечётное.
Если соединить вершину равностороннего треугольника, построенного на диаметре окружности не со второй, а с первой точкой деления диаметра окружности, при этом разделяя диаметр на n частей, то в результате получиться 2n – угольник.
Например, если разделить диаметр на пять равных отрезков, соединить вершину треугольника с первой точкой деления диаметра окружности, разделить всю окружность на дуги, равные полученной дуге. Соединить точки деления окружности и в результате получится правильный 10 – угольник.
При делении диаметра окружностей на 9 равных частей можно построить не только 9 –угольник, но и 6 – угольник, для этого нужно соединить вершину равностороннего треугольника с третьей точкой деления диаметра.
Построение пятиугольника, Приложение 20
Построение шестиугольника, Приложение 21
Построение семиугольника, Приложение 22
Построение девятиугольника, Приложение 23
Вывод: с помощью циркуля и линейки , используя простейшие построения я смогла построить произвольные и правильные многоугольники ( трех-, четырех-, пятиугольники и т.д.)
Литература:
Интернет – ресурсы
Учебник «Геометрия 7-9», Атанасян Л. С.
Приложения выполнены на листах: построения с помощью циркуля и линейки
Построение отрезка, равного данному
Построение угла, равного данному.
Построение биссектрисы угла
Построение перпендикулярной прямой через точку, лежащую на прямой.
Построение середины отрезка.
Построение перпендикулярной прямой через точку, не лежащую на прямой.
Построение произвольного треугольника.
Построение прямоугольного треугольника.
Построение равнобедренного треугольника.
Построение произвольного четырехугольника.
Построение четырехугольника с прямым углом.
Построение прямоугольника.
Построение произвольного пятиугольника.
Построение произвольного шестиугольника.
Построение равностороннего треугольника.
Построение квадрата.
Построение ромба.
Построение правильного шестиугольника. (1 способ).
Построение правильного шестиугольника. (2 способ).
Построение правильного пятиугольника.
Построение правильного шестиугольника (способ Н. Биона).
Построение правильного семиугольника (способ Н. Биона).
Построение правильного девятиугольника (способ Н. Биона).
5


















