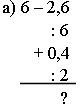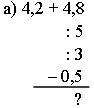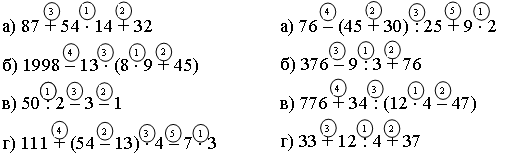Поурочное планирование

Урок № 135
Среднее арифметическое (п. 38)

Цели: научить давать определение среднего арифметического, находить среднее арифметическое чисел.

Оборудование: кодоскоп, кодопозитивы.

Ход урока

I. Сообщение темы урока.

Учитель: Вы часто слышите по телевизору, читаете в газете такие слова: средняя зарплата трудящихся, средний размер пенсии, средний удой молока, средний урожай с 1 га и т. д. Какое слово повторяется в этих словосочетаниях?

Выясним его смысл.

II. Объяснение нового материала.

На экран проецируется план работы с текстом.

1. Прочитайте внимательно задачу № 1, ее решение и ответьте на вопросы:

а) Какое действие выполнили с числами?

б) Почему сумму разделили на 3?

2. Прочитайте и запомните определение среднего арифметического нескольких чисел.

Закончите самостоятельно предложение: «Чтобы найти среднее арифметическое пяти чисел, нужно …».

3. Придумайте задачу, в которой нужно найти среднюю зарплату рабочего за день.

4. Найдите среднее арифметическое чисел 3,7; 2,4; 5,6.

Ответ: 3,9. Если допустили ошибку, выполните вычисления ещё раз.

III. Тренировочные упражнения.

1. № 1496, 1497 (б, в), 1502, 1500.

2. На повторение № 1516 (а, б) – самостоятельно, № 1512.

IV. Итог урока.

1. Повторить определение среднего арифметического.

2. Решите задачи:

а) В волейбольной команде двум игрокам по 21 году, трем по 20 лет и одному 24 года. Каков средний возраст игроков?

б) Найдите среднее арифметическое чисел: 23,86; 22,7 и 36,6.

3. Занимательный вопрос:

Девочка выходит к доске и пишет: «Двести сорок да двести сорок будет четыреста сорок». Девочка не ошиблась. В чем дело?

V. Домашнее задание: п. 38 (до задачи № 2); № 1524 (а), 1525, 1534 (а). В математический словарь: среднее арифметическое.

Урок № 136
Среднее арифметическое (п. 38)

Цели: сформировать понятие средней скорости движения и научить находить среднюю скорость движения.

Оборудование: плакат для устных упражнений.

Ход урока

I. Проверка домашнего задания.

1. Консультанты докладывают о результатах выполнения домашнего задания.

2. Соседи по парте обмениваются тетрадями и сверяют решение № 1524 (а) и 1534 (а) с доской.

II. Устные упражнения.

1. Вычислите:

3,18 – 1,08 2,06 + 1,04 5,4  0,1 4,08 : 4.

2. Выполните деление: 40 : 0,4 0,8 : 0,2 100 : 0,1

3. Найдите сумму результатов вычислений:

5,77 + 0,23 2,85 – 1,85 0,8  0,5 0,5  2.

4. Может ли произведение двух чисел оказаться меньше одного из множителей? Меньше обоих множителей? Примеры. Может ли частное оказаться больше делимого? Приведите примеры.

III. Изучение нового материала.

Работа с текстом по плану:

1. Прочитайте условие задачи № 2. О каких величинах в задаче идет речь?

2. Внимательно прочитайте решение задачи № 2. Что обозначают произведения 4,6  2; 5,1  3? Что обозначает выражение

4,6  2 + 5,1  3?

Что обозначает частное 24,5 : 5? Как по-другому называют эту скорость?

3. Каким еще способом можно вычислить среднюю скорость движения?

4. Придумайте задачу, в которой нужно вычислить среднюю скорость движения.

5. Какие ещё средние величины можно вычислить таким же способом?

6. Прочитайте задачи и скажите, как будете отвечать на поставленные в них вопросы.

Задача № 1

За первый час лыжник прошел 10,8 км, за второй 9,4 км и за третий 9,1 км. Сколько километров в среднем проходил лыжник за час?

Задача № 2

Токарь точил три одинаковые детали. Первую деталь он обточил за 1 мин, вторую за 56 с и третью за 1 мин 1 с. Какое время в среднем он затратил на обработку одной детали?

Задача № 3

Взвешиванием установили массы пяти овец: 28,5 кг, 32,6 кг, 35,1 кг, 30,3 кг и 27 кг. Вычислить среднюю массу овец.

III. Работа по теме урока.

1. № 1495 (а); 1499.

2. Задача. Велосипедист ехал 3 ч со скоростью 14 км/ч и 2 ч со скоростью 18 км/ч. Найдите среднюю скорость велосипедиста за все время движения.

3. № 1503.

4. На повторение № 1516 (в, д), 1517 (а).

IV. Итог урока.

Решите задачу (комментирование с места).

1. Мотоциклист проехал 100 км со скоростью 50 км/ч и ещё 120 км со скоростью 40 км/ч. Найдите среднюю скорость мотоциклиста на всем пути.

2. Найдите среднее арифметическое чисел: 4,27; 4,05; 3,22; 3,76; 4 и 4,16.

3. Сценка.

1-й ученик: Из парикмахерской я вышел остриженным наголо. Лето, жарко. Иду и радуюсь. Навстречу мне приятель, очень любознательный и хитроумный парень.

2-й ученик: Привет. Что же это ты столько волос оставил на голове?

1-й ученик делает удивленное лицо, пожимает плечами, разводит руки в стороны.

2-й ученик: Сколько, по-твоему, метров волос осталось у тебя на голове?

1-й ученик: Метр-два, может быть, и будет, если собрать все остатки.

2-й ученик рассмеялся: «Ошибся. И во много раз. Подумай как следует, прежде чем ответить на этот простой с первого взгляда вопрос».

Пауза.

2-й ученик: Считая, что после стрижки остаются волосы длиной в 0,1 см, а число их на голове человека в среднем равно 200 000, можно получить удивительный итог: после стрижки «наголо» на голове остается около 200 м волос.

V. Домашнее задание: п. 38; № 1486 (б), 1524, 1526, 1534 (а).

Урок № 137
Среднее арифметическое (п. 38)

Оборудование: ксерокопии тестов, таблицы для заполнения ответов, калька.

Ход урока

I. Выполнить тест (у каждого ученика свой лист с тестом).

Вариант I

1. Найдите среднее арифметическое чисел: 0,1; 4,4; 6.

1) 5,25; 2) 3,5; 3) 1,7; 4) 2,85.

2. Вычислите: 3,57 + 2,23 – 4,8.

1) 10,7; 2) 1; 3) 5,79; 4) 1,3.

3. Вычислите: (17,28 : 3,2 + 1,4  2,5) : 89 + 1,9.

1) 1,1; 2) 2; 3) 2,9; 4) 11,9.

4. Решите уравнение: 1,5х – 1,15 = 1,1

1) х = 2,25; 2) х = 0,75; 3) х = 2,16; 4) х = 1,5.

Фамилия, имя ___________________________ класс_______
№ задания	1	2	3	4
№ ответа

Вариант II

1. Найдите среднее арифметическое чисел: 4,7; 3; 0,1.

1) 1,7; 2) 3,9; 3) 2,55; 4) 2,6.

2. Вычислите: 4,67 + 3,23 – 5,8.

1) 13,7; 2) 2,2; 3) 2,1; 4) 7,24.

3. Вычислите: (37,41 : 4,3 + 1,3  2,6) : 4.

1) 41,06; 2) 2,3; 3) 3,02; 4) 0,302.

4. Решите уравнение: 2,5х – 3,15 = 2,1

1) х = 2,75; 2) х = 13,175; 3) х = 0,42; 4) х = 2,1.

Фамилия, имя ___________________________ класс_______
№ задания	1	2	3	4
№ ответа

II. Работа по теме урока.

1. № 1501, 1498, 1506, 1509.

2. Среднее арифметическое трёх чисел 0,43. Первое в 1,5 раза больше второго. Найдите эти числа.

3. На повторение № 1516 (г), 1517 (б), 1518.

4. Может ли произведение двух чисел оказаться меньше одного из множителей? Меньше обоих множителей? Примеры. Может ли частное оказаться больше делимого? Приведите примеры.

III. Итог урока.

1. Имеется 9 чисел. Их среднее арифметическое 14,2. Среднее арифметическое первых пяти чисел 12,6. Найдите среднее арифметическое остальных чисел.

IV. Домашнее задание: п. 38; № 1527, 1529, 1535 (б). Повторить п. 32–37 (повторить все правила).

Урок № 138
Среднее арифметическое (п. 38)

Оборудование: плакат с вопросами.

Ход урока

I. Устные упражнения.

1. «Математическая перестрелка».

Вывешивается плакат с вопросами, три ряда – три команды. (Вопросы можно взять из тех, которые даны после пункта, команды по очереди задают их друг другу.)

2. № 1510 (г), 1511 (д, е), 1512.

3. «Думай и соображай».

а) Какой знак можно поставить между числами 7 и 8, чтобы получившееся число было больше 7 и меньше 8.

б) Между числами 5,2 и 5,3 поставьте число, большее 5,2 и меньшее 5,3.

II. Работа по теме урока.

1. № 1497 (г).

2. Среднее арифметическое трёх чисел 3,5. Второе число больше первого в 2,5 раза, а третье число больше второго на 0,6. Найдите каждое из этих чисел.

3. С поля площадью 23,4 га собрали по 5,2 ц гречихи с 1 га; с поля площадью 19,5 га собрали по 4,8 ц гречихи с 1 га и с поля площадью 15,6 га собрали по 5,4 ц гречихи с 1 га. Найдите среднюю урожайность гречихи с 1 га на этих трех полях.

III. Итог урока.

Самостоятельная работа

Вариант I	Вариант II
1. Найти среднее арифметическое чисел:
13,84; 14,23; 12,66 и 15,03.	23,12; 24,23; 22,11 и 25,06
2. Турист шел 6 ч со скоростью 5 км/ч и 2 ч ехал на автомашине со скоростью 45 км/ч. Найдите среднюю скорость движения туриста на всем пути.	2. Поезд шел 2 ч со скоростью 80 км/ч и 3 ч со скоростью 90 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.
3. Среднее арифметическое двух чисел равно 1,36. Одно число в 2,4 раза меньше другого. Найдите эти числа.	3. Среднее арифметическое двух чисел 1,68. Одно число в 3,2 раза больше другого. Найдите эти числа.
4. Среднее арифметическое четырех чисел 1,4, а среднее арифметическое трех других чисел равно 2,1. Найдите среднее арифметическое этих семи чисел.	4. Среднее арифметическое пяти чисел равно 2,4, а среднее арифметическое трех других чисел 3,2. Найдите среднее арифметическое этих восьми чисел.

IV. Домашнее задание: п. 38, повторить п. 32–37; № 1530, 1532, 1535 (б). № 1512 – выучить таблицу. Подготовиться к контрольной работе.

Урок № 139
Контрольная работа № 11 (п. 36–38)

Вариант I

1. Выполните действия:

а) 3,2  5,125; б) 0,084  6,9; в) 60,03 : 8,7; г) 36,4 : 0,065.

2. Найдите значение выражения (21 – 18,3)  6,6 + 3 : 0,6.

3. В магазин привезли 10 ящиков яблок по 3,6 кг в одном ящике и 40 ящиков яблок по 3,2 кг в ящике. Сколько в среднем килограммов яблок в одном ящике?

4. Из одного гнезда одновременно вылетели в противоположные стороны две вороны. Через 0,12 ч между ними было 7,8 км. Скорость одной вороны 32,8 км/ч. Найдите скорость полета второй вороны.

5. Как изменится число, если его разделить на 0,25? Приведите примеры.

Вариант II

1. Выполните действия:

а) 1,6  7,125; б) 0,069  5,2; в) 53,82 : 6,9; г) 32,3 : 0,095.

2. Найдите значение выражения (41 – 38,7)  8,8 + 4 : 0,8.

3. Для обшивки стен использовали 8 досок длиной 4,2 м каждая и 12 досок 4,5 м каждая. Найдите среднюю длину одной доски.

4. С одного цветка одновременно вылетели в противоположные стороны две стрекозы. Через 0,08 ч между ними было 4,4 км. Скорость одной стрекозы 28,8 км/ч. Найдите скорость полета другой стрекозы.

5. Как изменится число, если его умножить на 0,25? Приведите примеры.

Домашнее задание: решить другой вариант; принести на следующий урок микрокалькулятор.

Урок № 140

Микрокалькулятор (п. 39)

Цели: научить правилам вычисления на МК, вычислять с помощью МК и составлять программу вычислений.

Оборудование: плакаты с «табло» и «клавиатурой» МК, с примерами; вопросы к п. 39.

Ход урока

I. Анализ контрольной работы.

II. Изучение нового материала.

Работа с текстом по плану:

1. При помощи какого инструмента выполняют вычисления?

2. Какие арифметические действия можно выполнять с помощью микрокалькулятора?

3. С чего начинается работа на микрокалькуляторе?

4. Как ввести в микрокалькулятор натуральное число? Десятичную дробь?

5. Как сбросить число с индикатора?

6. Выполните действия на микрокалькуляторе.

Вывешивается плакат.

СЛОЖЕНИЕ
Задание	2,5 + 0,6 =
Последовательность операций	2,5 0,6 3,1
ВЫЧИТАНИЕ
Задание	2,5 – 0,6 =
Последовательность операций	2,5 0,6 1,9
УМНОЖЕНИЕ
Задание	10,5  3 = 31,5
Последовательность операций	10,5 3 31,5
ДЕЛЕНИЕ
Задание	10,5 : 3 = 3,5
Последовательность операций	10,5 3 3,5

7. Почему прибор называется «микрокалькулятор»?

От греческого слова «mikros» – малый, от латинского слова «calculation» – счет, вычисления.

III. Закрепление.

1. № 1536, 1537, 1539 (а, б), 1538 (а–г) (1-е пары чисел), 1540 (а, д).

2. На повторение № 1548 (а), 1555 (а, б), 1549.

IV. Итог урока.

1. Обратить внимание на правильное написание слов: микрокалькулятор, табло, индикатор, клавиатура, клавиши.

2. Ответить на вопросы п. 39.

3. Вычислить с помощью калькулятора: 871,017 : 5,05 – 11,376.

V. Домашнее задание: п. 39; № 1556 (а–г), 1557 (а), 1559, 1547. Прочитать с. 317 (об истории развития вычислительных устройств). В математический словарь: микрокалькулятор.

Урок № 141

Микрокалькулятор (п. 39)

Оборудование: листочки для записи ответов к устным заданиям.

Ход урока

I. Проверка домашнего задания.

1. Сообщение консультантов о результате выполнения домашнего задания.

2. Проверить правильность решения № 1557 (а), 1559, 1545.

II. Устные упражнения.

1. Составить задачу по числовому выражению:

(3,8 + 3,7 + 3,6) : 3.

а) Как по-другому можно назвать это выражение?

б) Что называется средним арифметическим?

2. Задания по вариантам: устно вычислить и записать только ответ.

Вариант I	Вариант II
б) Выполнить деление:
; 1 : 2: 0,8 : 0,04.	; 5 : 0,2; 1 : 1,25
в) Каким одним действием можно уменьшить число в 10 раз?	в) Каким одним действием можно уменьшить число в 100 раз?
г) Каким одним действием можно увеличить число в 1000 раз?	Каким одним действием можно увеличить число в 100 раз?

Листы сдаются на проверку.

III. Работа по теме урока.

1. № 1539 (в, г), 1538 (а–г) (2-е и 3-и пары чисел), 1540 (б, г).

2. На повторение № 1546 (б), 1551, 1555 (в), 1553.

IV. Итог урока.

1. Вопросы к п. 39.

Самостоятельная работа

Вариант I	Вариант II
а) Вычислите с помощью микрокалькулятора:
43,5  (387,38 + 392,43) – 920,035 94,27  3,796 : 4,7135 – 5,38 (438,25322 : 53,78 + 24,051)  4,2867 3,22226 : 4,39  0,245 – 0,04483	(4,3257 + 2,8345)  53,9 – 5,00478 5,843  74,86 : 2,9215 + 30,28 (377,26366 : 431,8 + 0,7463)  39,831 72,4176 : 85,6  4,35 – 0,0584

V. Домашнее задание: п. 39; № 1556 (д, е), 1557 (б), 1560, 1558.

Урок № 142

Проценты (п. 40, ч. 1)

Цели: научить давать определение процента, обозначать, читать и находить процент чисел и величин, переводить процент в десятичную дробь и обратно.

Оборудование: плакаты для устных упражнений и объяснения нового материала.

Ход урока

I. Устные упражнения.

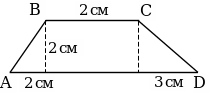
1. Квадрат ABCD разделен на равные части. Площадь заштрихованной фигуры равна 6 м². Найдите площадь квадрата AВCD.

(Вывешивается плакат.)

2. Учитель: Если вы правильно выполните вычисления и выпишите в таблицу буквы, соответствующие найденным ответам, то узнаете тему сегодняшнего урока.

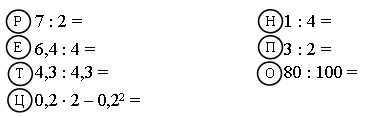
Примечание: сначала вычисляются примеры, а потом открывается таблица.

	3,5	0,8	0,36	1,6	0,25	0,1

Итак, тема нашего урока «Проценты».

II. Изучение нового материала.

1. Объяснение можно проводить методом беседы.

Вопросы: 1) Сколько килограммов в одном центнере? (100 кг). Какую часть центнера составляет 1 кг? (0,01).

2) Сколько сантиметров в одном метре? (100 см)

Какую часть метра составляет 1 см? (0,01)

3) Сколько ар в одном гектаре? (100 а)

Какую часть гектара составляет 1 а? (0,01)

4) Принято называть сотую часть любой величины или числа процентом. Слово «процент» происходит от латинского «центи» (по- французски «санти»), указывающего на уменьшение единицы измерения в 100 раз. Для краткости слово «процент» после числа заменяют знаком «%».

5) Записать в тетради:

6) Предлагается ученикам найти определение процента, прочитать и запомнить. В тетради записывается определение процента:

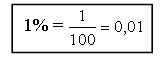
7) Как правильно читать? (Читают соответствующий абзац пункта до задачи № 1.)

8) Запомнить равенства: (вывешивается плакат).

0,1 = = 10% 0,25 = = 25% 0,5 = = 50%

0,75 = = 75% 1 = 100%

III. Закрепление.

1. Повторить по вопросам:

а) Что называется процентом?

б) Как называют 1% от центнера, метра, гектара, рубля?

2. Решить № 1561 (1–3), 1562 (1–3), 1563 (1–3), 1566, 1567.

3. На повторение № 1594.

IV. Итог урока.

1. Тест.

1) Процент – это:

а) тысячная часть числа; б) сотая часть числа;

в) десятая часть числа.

2) 8% – это:

а) 0,08; б) 0,8; в) 0,007; г) 0,0007.

3) 0,269 – это:

а) 269% б) 2,69% в) 26,9% г) 0,269%.

4) 25% класса – это:

а) половина учеников класса; б) четверть учеников класса;

в) пятая часть класса; г) двадцать пятая часть класса.

2. Составьте текст задачи, используя чертеж:

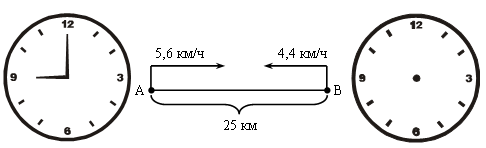
Узнайте и покажите на циферблате часов, когда пройдет встреча, если указано время выхода.

V. Домашнее задание: п. 40 (до задачи № 1); № 1596, 1599, 1602 (а). В математический словарь: процент.

Урок № 143
Проценты (п. 40, ч. 2)

Цели: научить решать задачи на проценты.

Оборудование: плакат с «лабиринтом» для устных упражнений.

Ход урока

I. Устные упражнения.

1. «Лабиринт». Заполнить пропуски числами:

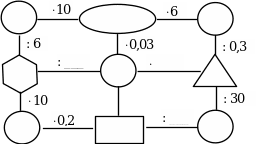
2. Задача. Лучшим ученикам подарили 100 книг, причем каждый получил по 5 книг. Сколько процентов составляют книги, полученные каждым учеником?

3. Задача. На пастбище было 100 животных: 39 телят, 52 овцы, а остальные козы. Сколько процентов от общего количества животных составляют овцы, телята и козы?

II. Изучение нового материала.

1. Разработать и решить задачи № 1 и № 2 из п. 40.

2. Какое сходство у этих задач в решении? Чем отличаются эти задачи?

III. Закрепление.

1. Закончить № 1561, 1562, 1563, 1565, 1569, 1573, 1572.

2. На повторение № 1592 (а), 1599.

3. На повторение № 1594.

IV. Итог урока.

1. Как правильно говорить и читать?

2. Исторические сведения о процентах и их обозначении.

Урок № 144

Проценты (п. 40, ч. 3)

Цели: научить находить процентное отношение величин.

Оборудование: ксерокопии тестов, таблица для ответов, калька.

Ход урока

I. Проверка домашнего задания.

Выполнить тест.

Вариант I

1. 4% – это:

1) 0,4 2) 0,004 3) 0,04 4) 0,0004

2. 0,103 – это:

1) 1,03% 2) 10,3% 3) 103% 4) 0,103%

3. 20% избирателей – это:

1) двадцатая часть избирателей 2) половина избирателей

3) четвертая часть избирателей 4) пятая часть избирателей.

4. При помоле пшеницы получается 80% муки. Сколько муки получится из 90 тонн пшеницы?

1) 112,5 т 2) 10 т 3) 72 т 4) 7200 т.

5. За первую половину урока Петя выполнил 60% задания, а за вторую – 27%. Сколько процентов задания не выполнил Петя?

1) 13% 2) 33% 3) 23% 4) 87%.

6. Найдите число, если 12% от него составляет 30.

1) 42; 2) 3,6 3) 2,5 4) 250.

Вариант II

1. 7% – это:

1) 0,07 2) 0,7 3) 0,007 4) 0,0007

2. 0,204 – это:

1) 204% 2) 2,04% 3) 20,4% 3) 0,204%

3. 25% учеников класса – это:

1) половина учеников класса;

2) четверть учеников класса;

3) пятая часть учеников класса;

4) двадцать пятая часть учеников.

4. 40% от 70 равно:

1) 28 2) 30 3) 175 4) 2800.

5. За первую минуту спортсмен пробежал 18% дистанции, а во вторую – 30%. Сколько процентов дистанции осталось преодолеть бегуну?

1) 48% 2) 12% 3) 62% 4) 52%.

6. В шкафу было 60 учебников, что составляет 40% имеющихся там книг. Сколько было книг в шкафу?

1) 24; 2) 100 3) 150 4) 15.

Таблица ответов для каждого варианта.

Фамилия, имя_________________________ класс________
№ задания	1	2	3	4	5	6
№ ответа

Работу сдают на проверку.

II. Изучение нового материала.

1. Разработать и решить задачи № 3 из п. 40.

2. Как обратить десятичную дробь в проценты?

3. Как перевести проценты в десятичную дробь?

III. Закрепление.

1. Закончить № 1564.

2. № 1568, 1575, 1580.

3. На повторение № 1592 (б), 1596.

IV. Итог урока.

1. Таблица процентов:

а) перевести в проценты:

б) перевести в десятичную дробь: 10%, 1; 0,5; 0,02; 0,05; 0,2.

2. Дан прямоугольник:

Если его площадь принять за 100%, то площади других прямоугольников будут составлять:

а) ________% б) ________%

в) ______% г) _____%.

V. Домашнее задание: п. 40 (весь); № 1600, 1603, 1612 (б).

Урок № 145

Проценты (п. 40)

Оборудование: ксерокопии заданий; игрушки для «магазина», «ценники», плакат о снижении цен.

Ход урока

I. Устные упражнения.

1. Выполнить действия (написано на доске).

а) 0,25 : = б) 7,5 : = в) 6 : 10 =

г) 11,11 : 11 = д) 1,634  5 = е) 7 – 7 : 10 =

ж) 1 : 0,2 – 0,2 = з) 1,63  5 =

II. Работа по теме урока (каждому ученику выдается ксерокопия задания № 1 и № 2).

1. Найдите:

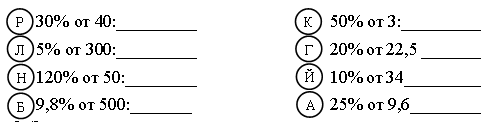
2. Заполните пропуски:

3. Выполните действия:

(0,32  3,5 6 0,25 + 0,02)  3,2 + 321,6 =

4. Заполните пропуски в тексте:

49	2,4	3,4	1,5		15

– самое глубокое озеро в мире. Его называют «жемчужной» нашей планеты, так как в нем самая чистая вода. Его глубина составляет . В него впадает больших и малых рек, а вытекает лишь одна –

2,4	60	4,5	2,4	12

Задание № 2

В тексте «Вода на Земле» замените буквенные обозначения х, у, t и m числами, предварительно выполнив математические задания. Прочитайте текст с учетом найденных значений.

Вода на Земле

% поверхности Земли покрыто водой. Пресная вода составляет % от всех водных запасов.

% всей пресной воды находится в озере Байкал.

% всей пресной воды содержится в ледниках Арктики и Антарктиды.

х =(0,2² + 9,96)  6,7 = _______________

у = 1,5  4 – 0,5  8 = ________________

t = = ________

m = 2,3  3  (3² + 0,2  5) = ____________

5. Быстро оформляется «витрина магазина»: выставляются игрушки и вывешивается объявление

К товару прикрепляются ценники, в которых зачеркнута старая цена, нужно внести изменения в ценники.

Назначается «директор магазина», который приглашает несколько «бухгалтеров», которые на доске выполняют нужные вычисления.

6. Разобрать устно решение задач № 1570, 1574, 1576.

7. Решить письменно № 1582.

III. Самостоятельная работа (обучающая, можно посадить парами «сильный – слабый»).

Задача № 1

Из овса получается 40% муки. Сколько муки получится из 26,5 т овса?

Задача № 2

Засеяли 65% поля, что составляет 325 га. Найдите площадь всего поля.

Задача № 3

В старших классах 120 учащихся. Из них 102 ученика работали летом на ферме. Сколько процентов учащихся старших классов работали летом на ферме?

IV. Домашнее задание: п. 40; № 1602, 1604, 1552. Подготовиться к самостоятельной работе.

Урок № 146
Задачи на проценты (п. 40)

Оборудование: плакат для устных вычислений.

Ход урока

I. Устные упражнения.

Вывешивается плакат.

1. Из пункта А одновременно в противоположных направлениях отправились лодка и плот. Собственная скорость лодки – 12 км/ч. Через 1 час плот оказался в пункте В, а лодка – в пункте С.

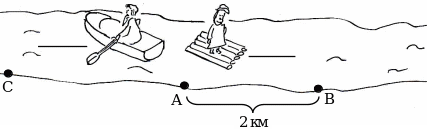
1) Какова скорость течения реки?

2) С какой скоростью движется лодка?

3) Какое расстояние проплыла лодка?

4) Какое расстояние будет между участниками движения, если они будут плыть еще 1 час?

5) Сколько времени пройдет с момента отплытия из пункта А, когда расстояние между ними будет 30 км?

2. № 1591.

II. Работа по теме урока.

1. Решить двумя способами № 1571.

2. № 1577, 1585, 1584.

III. Самостоятельная работа.

Вариант I	Вариант II
1. В первый день вспахали 100 га, во второй 150 га. Сколько процентов всей этой площади вспахали в первый день?	1. В первую смену засеяли 270 га, а во вторую – остальные 180 га. Сколько процентов всей площади засеяли в первую смену?
2. Никелевая руда содержит 4% никеля. Сколько никеля содержится в 150 т такой руды?	2. В железной руде содержится 54% железа. Сколько тонн железа содержится в 475 т такой руды?
3. Заасфальтировав 27,5 км дороги, ремонтники тем самым выполнили 25% плана. Сколько километров дороги надо заасфальтировать по плану?	3. Ученик прочитал 35 страниц. Это составляет 17,5% книги. Сколько страниц в книге?
4. Выполнить действия: (3,1  5,3 – 14,39) : 1,7 + 0,8	4. Выполнить действия: (21,98 – 4,2  4,6) : 1,9 + 0,6.
5. Необязательное задание.
В двух корзинах по 25 кг винограда. Вначале из первой корзины взяли 20% имевшегося там винограда и положили его во вторую корзину. Потом из второй корзины взяли 20% оказавшегося там винограда и положили в первую. В какой корзине винограда больше и насколько?	В двух корзинах по 32 кг яблок. Вначале из первой корзины взяли 25% имевшихся там яблок и положили их во вторую корзину. Потом из второй корзины взяли 25% оказавшихся там яблок и положили их в первую. В какой корзине яблок стало больше и насколько?

IV. Домашнее задание: п. 39, 40; № 1605, 1607, 1610. Подготовиться к контрольной работе.

Урок № 147
Контрольная работа № 12 (п. 39–40)

Вариант I	Вариант II
1. Надоили 150 л молока. После того как отправили молоко в детский сад, осталось 80% имевшегося молока. Сколько литров молока отправили в детский сад?	1. В ящике 120 кг риса. Через несколько дней в ящике осталось 25% находившегося там риса. Сколько килограммов риса взяли из ящика?
2. Смешали 4 кг сушеных яблок и 6 кг сушеных груш. Сколько процентов полученной смеси составляют яблоки?	2. В поселке построили 16 одноэтажных и 4 двухэтажных дома. Сколько процентов всех построенных домов составляют одноэтажные дома?
3. Решите уравнение:
11 + 2,3у + 1,3у = 38	2,3у + 31 + 2,5у = 67
4. Найдите значение выражения:
102 –(155,4 : 14,8 + 2,1)  3,5	(42 – 149,1 : 14,2)  5,3 + 6,15
5. В коробке были карандаши. Сначала из коробки взяли 50% карандашей, а затем 40% остатка. После этого в коробке осталось 3 карандаша. Сколько карандашей было в коробке первоначально?	5. На полке стояли книги. Сначала с полки сняли 25% всех книг, а потом 70% оставшихся книг. После этого на полке осталось 27 книг. Сколько книг было на полке первоначально?

Домашнее задание: 1) Решить другой вариант.

2) Повторить п. 2 и 3.

Урок № 148
Угол, обозначение. Сравнение углов (п. 41)

Цели: научить давать определение угла, находить вершины угла, стороны, обозначать углы, определять углы.

Оборудование: плакат для устных упражнений; цветные мелки; модель часов.

Ход урока

I. Устные упражнения.

1) Какие фигуры изображены на плакате.

Как обозначается луч?

Как называется точка О?

Можно ли измерить длину луча?

Почему?

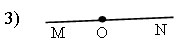Что делает точка, лежащая на прямой?

Как называются лучи ОМ и ON?

II. Изучение нового материала.

План изучения:

1. Определение угла, сторон угла, вершины угла.

2. Обозначение угла.

3. Точки, лежащие внутри угла, вне угла, на сторонах угла.

4. Сравнение углов с помощью наложения.

5. Определение развернутого угла.

III. Закрепление.

1. Повторить по вопросам изучаемый материал.

2. Выполнить № 1613, 1615, 1617.

3. На повторение № 1631, 1632.

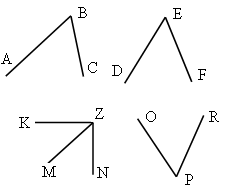
4. Запишите обозначение углов, изображенных на рисунке. Назвать стороны и вершину каждого угла.

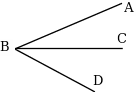
IV. Итог урока.

Тест

1. Стороны угла – это:

а) отрезки; б) лучи; в) прямые.

2. На рисунке изображен угол:

а) О; б) KZO; в) ZKO.

3. На рисунке изображено:

а) 3 угла; б) 5 углов; в) 6 углов.

V. Домашнее задание: п. 41 (до определения прямого угла); № 1638, 1639, 1643. В математический словарь: угол, стороны угла, вершина угла.

Урок № 149
Прямой и развернутый углы.
Чертежный треугольник (п. 41)

Цели: сформировать понятие развернутого угла, научить формулировать определение прямого угла и строить его при помощи чертежного треугольника.

Оборудование: модель часов, лист бумаги, чертежный треугольник, плакат с развернутым и прямым углами.

Ход урока

I. Письменный опрос по домашнему заданию.

Вариант I	Вариант II
1. Начертите угол NOK, отметьте точку А внутри угла, точку В вне угла и точку С на стороне угла.	1. Начертите угол PNS, отметьте точку М внутри угла, точку А на стороне угла и точку К вне угла.
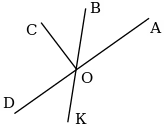
2. Запишите обозначение углов, изображенных на рисунке.

Для каждого угла назвать стороны и вершину, данные занести в таблицу.

Название угла	Стороны	Вершина

II. Устные упражнения.

1. На доске начерчена таблица, нужно заполнить её.

х	Формула решения	х = 10	х = 4	х = 1,2
50% от х
20% от х
120% от х
х% от х

2. № 1624 (б, в).

3. Блиц-турнир.

Проанализируйте данные чертежи. Запишите, как найти расстояние между участниками движения через 2 часа после одновременного выхода:

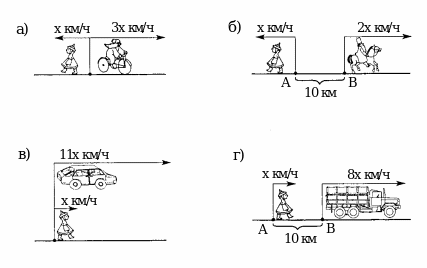
III. Изучение нового материала.

1. Вспомнить определение дополнительных друг другу лучей, сформулировать понятие развернутого угла, продемонстрировать развернутый угол на модели часов.

2. Продемонстрировать, как при сгибании листа два раза получаются 4 угла, дать определение прямого угла.

3. Построение прямого угла при помощи чертежного треугольника.

IV. Закрепление.

1. № 1613, 1619.

2. По рисунку найти развернутые и прямые углы.

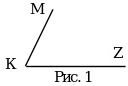
3. № 1616, 1620 (устно), 1618, 1621.

4. На повторение № 1634, 1636.

V. Итог урока.

1. Ответить на вопросы:

а) Какие лучи называют дополнительными?

б) Какой угол называют развернутым?

в) Дать определение прямого угла.

г) Рассказать и показать у доски, как с помощью чертежного треугольника построить прямой угол.

2. Самостоятельная работа (обучающая).

а) Проведите луч ОК. Постройте прямой угол, одной из сторон которого является луч ОК.

б) Начертите угол, который образуют стрелки часов, когда часы показывают 4 часа. Получится:

1) развернутый угол;

2) прямой угол;

3) не развернутый и не прямой.

VI. Домашнее задание: п. 41 (2); № 1640, 1645, 1642 (а), 1646 (а, б). В математический словарь: прямой угол, развернутый угол.

Урок № 150
Прямой и развернутый углы.

Чертежный треугольник (п. 41)

Оборудование: чертежный треугольник, индивидуальные карточки для письменного опроса.

Ход урока

I. Проверка домашнего задания. (Письменный опрос.)

Вариант I	Вариант II
1. Найдите с помощью чертежного треугольника прямые углы.
2. Начертите четыре луча АВ, АС, AD и АК. Запишите названия шести углов, сторонами которых являются эти лучи.	2. Начертите четыре луча ВА, ВС, ВМ, BZ. Запишите названия шести углов, сторонами которых являются эти лучи.

II. Устные упражнения.

1. Выясните, какая фигура лежит сверху, какая в середине, а какая снизу. Заполните таблицу символами: .

Рис. 1 Рис. 2 Рис. 3

	Рис. 1	Рис. 2	Рис. 3
лежит сверху
лежит в середине
лежит снизу

2. Найдите число, если 5% этого числа равны: 100; 0,1.

3. Сколько процентов от 400 составляют числа: 200; 4; 40; 80?

4. Составьте задачу по числовому выражению: а) 0,09  200;

б) 208  0,4.

III. Работа по теме урока.

1. Повторение теоретического материала (плакат).

а) Как называется эта фигура?

б) Что называется углом?

в) Указать стороны и вершину угла.

а) Какой угол изображен на рисунке?

б) Какой угол называется развернутым?

в) Назовите стороны угла.

а) Какой угол изображен на рис. 3?

б) Дайте определение прямого угла.

Рис. 3

2. Выполните задания № 1616, 1620 (устно), 1628, 1621.

3. На повторение № 1633, 1635.

IV. Итог урока.

Самостоятельная работа. (Каждому ученику дается нелинованный лист бумаги с заданиями).

Вариант I	Вариант II
1. По рисунку назвать прямые и развернутые углы.
2. Построить квадрат со стороной 3,6 см.	2. Построить квадрат со стороной 4,3 см.
3. Построить прямоугольник, длина которого 5 см, а ширина 3 см. Вычислить периметр и площадь этого многоугольника.	3. Построить прямоугольник, длина которого равна 6 см, а ширина 2 см. Вычислить периметр и площадь этого многоугольника.

V. Домашнее задание: п. 41; № 1641, 1644, 1646 (в, г). Принести на урок транспортир (показать ученикам, что это за инструмент

Урок № 151

Транспортир, градус, алгоритм измерения углов
(п. 42, ч. 1)

Цель: научить давать определение градуса, обозначать его, измерять углы с помощью транспортира.

Оборудование: демонстрационный транспортир; кодоскоп, кодопозитивы.

Ход урока

I. Поверка домашнего задания.

1. Консультанты докладывают о выполнении домашнего задания.

2. Проверить № 1644, 1646 (в, г).

II. Устные упражнения.

1. Кто быстрее сосчитает?

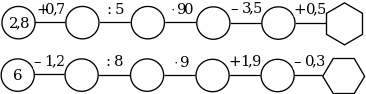
2. Назвать углы, изображенные на чертеже (задание проецируется на экран).

Найти среди этих углов прямые и развернутые углы.

III. Изучение нового материала.

На доске написан план.

1. Какой инструмент используют для измерения углов?

2. Как устроен транспортир?

3. Что такое градус? Каким знаком обозначают градус?

4. Как измеряют углы транспортиром?

Выделите три этапа: а) Совместить вершину развернутого угла на транспортире с углом, который мы измеряем; б) Один луч должен проходить через нулевую отметку (начало отсчета); в) второй луч проходит через отметку, которая показывает градусную меру угла.

IV. Закрепление.

1. № 1645, 1650, 1653 (устно), 1665, 1667.

V. Итог урока.

Повторить, как устроен транспортир, алгоритм измерения углов с помощью транспортира.

VI. Домашнее задание: п. 42 (ч. 1); № 1683, 1687, 1689. В математический словарь: транспортир, градус, алгоритм.

Урок № 152

Сравнение величин углов. Классификация углов
по градусной мере (п. 42, ч. 2)

Цель: научить давать определение прямого, тупого и острого углов, биссектрисы угла, находить равные углы, зная их градусную меру.

Оборудование: заранее написать на доске тезисы к новой теме и текст самостоятельной работы.

Ход урока

I. Проверка домашнего задания.

№ 1683, 1687, 1689.

II. Устные упражнения.

1. 5% некоторого числа равны 11. Найдите 15%, 20%, 35%, 50%, 100% этого числа.

2.

а) Число 60 увеличили на 15. На сколько процентов увеличилось число?

б) Число 75 уменьшили на 15. На сколько процентов уменьшилось число?

в) Некоторое число увеличили в 2 раза. На сколько процентов увеличилось число?

г) Некоторое число уменьшили в 2 раза. На сколько процентов уменьшилось число?

III. Изучение нового материала.

Изучение ведется методом беседы и поэтапно открываются основные тезисы темы:

1. Прямой угол равен 90.

2. Равные углы имеют равные градусные меры.

3. Острый угол меньше 90.

4. Тупой угол больше 90, но меньше 180.

IV. Закрепление.

1. Устно № 1660.

2. Письменно № 1661, 1666, 1669, 1668.

3. Повторение № 1678.

V. Итог урока.

Самостоятельная работа (выполняется на листочках).

1. Начертите какие-нибудь острый и тупой углы и обозначьте их. Измерьте каждый угол и запишите результаты измерений.

2. Луч разделил развернутый угол на два угла. Один из этих углов 56. Найдите градусную меру другого угла.

3. Начертите треугольник CDK, такой, что  CKD = 90. Измерьте два других угла этого треугольника.

VI. Домашнее задание: п. 42 (ч. 2); № 1684, 1686, 1688, 1692 (а). В математический словарь занести определения острого, прямого и тупого углов. (Дать указания к № 1686.)

Урок № 153
Сравнение величин углов. Классификация

углов по градусной мере (п. 42)

Цель: научить строить угол заданной градусной меры.

Оборудование: плакат для устных упражнений; ксерокопии тестов для домашнего задания.

Ход урока

I. Проверка домашнего задания.

№ 1684 (сверить с доской чертеж).

II. Устные упражнения.

1. Выполнить вычисления по схеме:

а)

2. Решить несколькими способами:

а) Найти 5% от 360; б) 15% от 350.

3. № 1653.

III. Работа по теме урока.

1. № 1651, 1656 (устно).

2. № 1657 (записать определение: луч, имеющий начало в вершине угла и делящий его на два равных угла, называется биссектрисой угла).

3. № 1659, 1663, 1662 (можно показать способ деления окружности на 6 равных частей).

4. На повторение № 1681 (комментирование с места).

IV. Домашнее задание: п. 42; № 1682, 1685, 1680, 1692 (б). Тесты (выдаются ксерокопии, каждому ученику свой вариант).

Вариант I

1. Для какого из углов верно обозначение:  PMК?

1) 2) 3) 4)

2. Определите вид угла ADK.

1) прямой; 2) тупой; 3) острый; 4) развернутый.

3. Каким является угол, если его градусная мера равна 97?

1) прямым; 2) тупым; 3) острым; 4) развернутым.

4. Измерить с помощью транспортира угол CBD. Выберите вариант ответа, наиболее близкий результату вашего измерения.

1) 114; 2) 112; 3) 66; 4) 116.

5. Луч МО лежит внутри угла AMB, причем  АМО = 48,  ВМО = 32. Определите градусную меру угла между АМВ.

1) 100; 2) 16; 3) 164; 4) 80.

6. Известно, что  СКО = 65. Определите градусную меру угла ОКВ.

1) 155; 2) 115; 3) 25; 4) 65.

Фамилия, имя ____________________________ класс______
№ задания	1	2	3	4	5	6
№ ответа

Вариант II

1. Для какого из углов верно обозначение:  ТРА?

1) 2) 3) 4)

2. Определите вид угла MNK.

1) тупой; 2) развернутый; 3) прямой; 4) острый.

3. Каким является угол, если его градусная мера равна 84?

1) развернутым; 2) острым; 3) прямым; 4) тупым.

4. Измерьте с помощью транспортира угол АBК. Выберите вариант ответа, наиболее близкий результату вашего измерения.

1) 113; 2) 69; 3) 67; 4) 65.

5. Луч AD лежит внутри угла КАС, причем  КАС = 45,  DAC = 18. Определите градусную меру угла между КАD.

1) 27; 2) 153; 3) 63; 4) 117.

6. Известно, что  МОА = 145. Определите градусную меру угла АОВ.

1) 55; 2) 35; 3) 125; 4) 145.

Фамилия, имя ____________________________ класс______
№ задания	1	2	3	4	5	6
№ ответа

V. Итог урока.

1. Проверить алгоритм построения углов заданной градусной меры.

2. Выполните задание:

а) Начертите угол АОВ, равный 80.

б) Отметьте на стороне ОА точку М, а на стороне ОВ точку К.

в) Соедините отрезком точку М и К.

г) Измерьте углы и стороны треугольника ОКМ. Вычислите периметр.

д) Заполните пропуски:

 МОК = …,  ОКМ = …,  ОМК – …,

ОК = …, ОМ = …, МК = …, Р_ = …

3. Луч ОЕ разделил СОD на два угла СОЕ и ЕОD. Найдите градусную меру угла CОD, если  СОЕ = 68, а  EOD = 37.

Урок № 154

Сравнение величин углов. Классификация

углов по градусной мере (п. 42)

Оборудование: демонстрационный транспортир, треугольник.

Ход урока

I. Проверка домашнего задания.

№ 1685, 1682.

II. Устные упражнения.

1. В зале кинотеатра 600 зрителей.

Определите: а) Сколько человек составляет 1%, 5%, 10%, 40% всех зрителей. б) Сколько процентов зрителей составляют 12 человек, 90 человек, 300 человек?

2. № 1680, 1654.

III. Работа по теме урока.

1. Устно № 1658, 1654.

2. Письменно № 1652, 1664.

IV. Самостоятельная работа.

Вариант I	Вариант II
1. Построить углы SDK и AMN, если  SDK = 90, а  AMN = 134.	1. Построить углы MNE и DBK, если  MNE = 112,  DBK = 90.
2. Начертите луч ОС и постройте с одной стороны этого луча угол АОС, равный 125, а с другой стороны угол DOC, равный 80.	2. Начертите луч РК и постройте с одной стороны этого луча угол DPK, равный 75, а с другой стороны угол FPK, равный 140.
3. Угол CBE разделен лучом ВК на два угла СВК и КВЕ. Угол СВК равен 63 и составляет угла СВЕ. Найдите градусную меру углов.	3. Угол CAF разделен лучом АВ на два угла САВ и BAЕ. Угол BAE равен 72 и составляет угла САЕ. Найдите градусную меру углов САЕ и САВ.
4. Из одной точки А проведены лучи AD, АВ и АМ так, что  DAВ = 130,  DAM = 170. Какую градусную меру может иметь угол BAM?	4. Из одной точки К проведены три луча КВ, КА и КС так, что  АКВ = 120,  ВКС = 140. Какую градусную меру может иметь угол АКС?

V. Домашнее задание: № 1671 (измерить углы и записать их градусную меру). Для любознательных № 1676.

Урок № 155

Круговые диаграммы (п. 43)

Цель: сформировать понятие диаграммы, научить читать и строить диаграммы.

Оборудование: различные круговые диаграммы; сигнальные карточки, модель часов.

Ход урока

I. Проверка домашнего задания.

1. Устно № 1671, 1690, 1691.

2. По вопросам повторить учебный материал п. 41, 42.

II. Устные упражнения.

1. Покажите зеленую карточку, если высказывание истинное, красную – если высказывание ложное.

а) Развернутый угол в три раза больше прямого.

б) Если  М = 90,1, то  М – тупой.

в) Проецируется на экран: на чертеже  А В.

г) Когда часы показывают 15 часов 30 мин, то стрелки образуют прямой угол.

2. Дано:  МРК и  СРК.

а) У этих углов общий луч РК;

б) у этих углов общая вершина К;

в) Если  МРК =  СРК, то РК – биссектриса  МРС.

3. «Страница для любознательных» (проводит ученик).

Основная единица измерения углов называется __________.

Но существуют и более мелкие единицы измерения углов. Например, ___________ (учащиеся записывают).

1 : 60 = = 1 – минута. Значит 1 = ___________

1 : 60 = = 1 – секунда. Значит 1 = _________.

Прочитайте: 1945; 1442456; 4521.

III. Изучение нового материала.

План:

1. Задача о магнитном железняке.

2. Изображение этого положения диаграммой.

3. Построение круговой диаграммы площадей океанов.

4. Привести примеры и продемонстрировать другие диаграммы.

IV. Закрепление.

1. № 1695, 1694.

2. На повторение: а) № 1702; б) начертите луч MN и постройте с одной стороны этого луча угол AMN, равный 124, а с другой стороны прямой угол CMN; в) Луч CD разделил угол KCF на два угла KCD и DCF. Найдите градусную меру угла KCF, если  KCD = 120, а угол DCF меньше угла KCD в 3 раза.

V. Итог урока.

1. Беседа по данной теме; сделать вывод и записать его в тетрадь: «Диаграмма – один из наглядных способов изображения зависимости между величинами».

2. Разобрать решение домашней задачи № 1706.

VI. Домашнее задание: п. 43; № 1706, 1703, 1709. Принести диаграммы. В математический словарь: диаграмма.

Урок № 156

Круговые диаграммы (п. 43)

Оборудование: заранее написать решение задачи № 1706 на доске; два вида демонстрационных треугольников, транспортир; кодоскоп.

Ход урока

I. Проверка домашнего задания.

1. № 1706 – сверить решение задачи с записями на доске.

II. Практическая работа.

1. На доске изображены контуры двух видов треугольников.

Ученик у доски измеряет углы на чертеже, другой измеряет углы непосредственно на треугольниках, за партами измеряют свои треугольники.

Ученики приходят к выводу, что существуют треугольники двух видов: с углами 90; 60; 30 и с углами 90; 45; 45.

Вопросы учителя.

1. Чему равна сумма всех углов треугольника?

2. Как не имея транспортира, только при помощи треугольников, построить угол в 120? 135? 150? 75? 105?

III. Устные упражнения.

1. № 1697 (в–д).

2. Проецируется на экран чертеж.

Вычислите градусную меру угла АОВ.

3. Вычислите неизвестные углы треугольника.

4. Найдите число, если 25% этого числа составляют 2; 10; 25; 0,5; 1,2.

5. Сколько процентов составляет:

а) 8 кг от 1 ц; б) 15 с от 1 мин; в) 35 см от 1 м?

IV. Работа по теме урока.

1. № 1696, 1693.

2. На повторение № 1705.

3. Самостоятельная работа (обучающая, посадить парами «сильный – слабый»).

а) Постройте углы РОК и SED, если  РОК = 27, а  SED = 127.

б) Луч CD разделил угол FCK на два угла FCD и DCK. Угол DCK равен 99 и составляет угла FCK. Найдите градусную меру углов FCK и FCD.

в) Из одной точки В проведены лучи ВС, ВА и BD так, что  АВС = 150 и  ABD = 90. Какую градусную меру может иметь  CBD?

V. Домашнее задание: п. 43; № 1707, 1708, 1710. Прочитать об истории развития геометрии. Подготовиться к контрольной работе.

Урок № 157

Контрольная работа № 13 (п. 41–43)

Оборудование: ксерокопии вариантов для каждого учащегося.

Вариант I

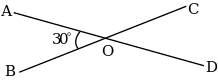
1. Измерьте углы ХОК и АОК, изображенные на рисунке. Вычислите градусную меру угла ХОА.

2. Постройте углы САВ, MNK и РОЕ, если  САВ = 53,  MNK = 90,  РОЕ = 108.

3. Луч ST делит прямой угол KSZ на два угла KST и TSZ. Найдите градусную меру угла TSZ, если угол KST составляет угла KSZ.

4. Луч АС делит развернутый угол MAN на два угла МАС и CAN. Найдите градусную меру этих углов, если угол CAN меньше угла МАС в 2,6 раза.

5. Два угла ADC и KDC имеют общую сторону DC. Какую градусную меру может иметь угол ADK, если  ADC = 130,  CDK = 30?

Вариант II

1. Измерьте углы MDC и MDК, изображенные на рисунке. Вычислите градусную меру угла CDK.

2. Постройте углы ВСА, KMN и ОРЕ, если  ВСА = 154,  KMN = 28,  ОРЕ = 90.

3. Луч MN делит прямой угол СMD на два угла CMN и NMD. Найдите градусную меру угла CMN, если угол NMD составляет угла CMD.

4. Луч BD делит развернутый угол ABC на два угла ABD и DBC. Найдите градусную меру этих углов, если угол ABD в 1,5 раза больше угла DBC.

5. Два угла KNM и PNM имеют общую сторону MN. Какую градусную меру может иметь угол KNP, если  KNM = 110,  PNM = 40?

Домашнее задание.

1. Решить другой вариант.

2. Повторить: действия с натуральными числами.

3. Повторить по этим пунктам математические термины, используя математический словарь.

Урок № 158

Повторение. Действия с натуральными числами

(урок-игра)

Оборудование: плакаты: «Счет и вычисления – основа порядка в голове» – И.Песталоцци; «Твой ум без числа ничего не постигает» – Николай Казанский; билеты для лотереи, много кружков красного и синего цвета, на кружках номера; музыкальное оформление.

Ход урока-игры

I тур. Лотерея.

Ученики разделились на 3 команды (каждая команда садится на свой ряд). По два человека от команды должны разыграть лотерею: вытащить билет и ответить на него. В билет включается теоретический материал по данной теме.

Пример заданий, предлагаемых участникам лотереи.

Билет № 1

а) Какие числа называются натуральными? Сколько цифр используют для написания чисел? Назвать эти цифры.

б) Как называются числа при умножении?

в) В каком порядке выполняются действия в выражении без скобок, если в нем встречаются только сложение и деление?

Билет № 2

а) Как называются числа при сложении? Может ли сумма быть равной одному из слагаемых?

б) Свойства умножения.

в) Записать число 365057000606 на доске, прочитать его и назвать классы.

Билет № 3

а) Как называются числа при вычитании?

Найти число а: а + а = а – а.

б) Что показывает частное? Всегда ли можно выполнить деление?

в) Назвать действия I ступени, II ступени.

Билет № 4

а) Как называют числа при делении?

б) Что показывает разность двух чисел?

в) Вычислить: 15².

Билет № 5

а) Как из суммы вычесть число? Привести пример.

б) Как называются числа при делении с остатком?

в) Вычислить: 4³.

Билет № 6

а) Как сравнить четырехзначное и трехзначное числа? Два шестизначных числа?

б) Как вычесть сумму из числа?

в) Как найти делимое при делении с остатком? Пример.

Если ответ правильный и полный, то участник лотереи и последующих конкурсов за каждый вопрос получает красный кружок; если правильный, но не полный – то синий кружок. Члены команды могут помогать, также получая красный кружок. Кружки с номерами выдаются соответственно произвольно.

II тур. Конкурс «бухгалтеров».

Вывешивается объявление: «Цены повышены на 2%» и ценники:

Под ценниками поместить картинки тех предметов, для которых нужно вычислить новую цену.

III тур. Конкурс «историков» команд.

Сообщают исторические сведения по данной теме, можно использовать другие книги по математике.

IV тур. Конкурс капитанов.

1. В карманах денег поровну. Из одного в другой карман положили 1 рубль. На сколько больше там стало?

2. Подсчитай, какое стадо обслужить ребятам надо.

Индюшат, их 240, водит Катя на пригорок.

Машет прутиком Илья, напевая:

«8 уток, один я, куда утки, туда и я».

Что-то громко чересчур раскричались курицы,

Сотен пять их было, и они как развоюются!

А на речке уток 200, как закрякали все вместе.

3. Сумма двух чисел больше одного из них на 17 и больше другого на 13. Чему равны эти числа?

4. Назовите число, если половина – треть его.

5. В саду 33 сучка, на каждом по 33 яблока. Сколько яблок всего?

6. Из спичек составлено равенство (открывается запись на доске), которое, как вы видите, неверное. Как переложить одну спичку, чтобы получить верное равенство?

V. «Хорошо ли ты усвоил действия с натуральными числами?»

На доске написаны 3 текста заданий с двумя вариантами. Капитаны вытаскивают номер своего задания и вся команда решает свое задание по вариантам.

Задание № 1

Вариант I	Вариант II
Вычислить:
1) 60000 – 408  120 + 1012  (24  10 – 235) 2) (8016  276 + 429  1014 – 264810) : 422	1) 805  712 – 304  501 + 834  (245  10 – 2300) 2) (708  398 – 892  211) : 93572 + 209

Задание № 2

Вариант I	Вариант II
Вычислить:
1) (10000 – 1867)  (10201 – 8634) + 204  18 2) (367710 : 35 + 302  49) – 50702 : 101	1) 901  701 + (20000 – 18904)  99 – 208  400 2) (1067154 : 4807 + 707  390) – 14904 : 23

Задание № 3

Вариант I	Вариант II
Вычислить:
1) 100000 + 60 (140000 – 702  120) + 24  400 2) (2875270 : 703 + (1499  508 – 448560 : 712)	1) (78213 – 74899)  217 + (300000 – 299809)  702 2) 428  1017 – (729 206 + 898656 : 1012)

Работы сдаются на проверку. За каждый правильно решенный пример – кружок красного или синего цвета. Подсчитывается количество кружков у каждого участника команды и выставляется оценка. Кроме этого, вывешивается таблица беспроигрышной лотереи по номерам, которые записаны на кружках.

VI. Домашнее задание: № 1716, 1717 (5, 6, 7). Повторить п. 2, 3, 20, 22, 41, 42, 43.

Урок № 159
Геометрические фигуры

(игра «Поле чудес»)

Оборудование: учебники за старшие классы; барабан; задания для выбора тройки и вопросы тройкам; плакаты с чертежами геометрических фигур; музыкальное оформление.

Ход урока

I. Вводная беседа учителя: что такое геометрическая фигура, вспомнить изученные фигуры, найти их на плакате, дать определение; какая наука изучает свойства геометрических фигур; показать учебники, по которым ученики будут заниматься в старших классах.

Объяснить правила игры «Поле чудес»:

а) Выбор троек игроков после правильного ответа на вопрос.

б) Барабан представлен на рисунке.

Обозначение секторов:

 – открыть первую букву;

 – назвать букву;

 – открыть последнюю букву;

 – совет друга;

 – переход хода.

II. Выбор первой тройки:

Вопросы:

1. Сосчитать, сколько углов, меньших 180, изображено на рисунке.

Ответ: 10 углов.

2. На рисунке изображены 4 угла. Величина одного из них известна. Найти градусные меры остальных трех углов.

3. Как убедиться, что площадь треугольника ACD больше площади треугольника DCE в 2 раза?

Задание. Как называется фигура, которая получается от вращения прямоугольного треугольника вокруг катета (принадлежность клоуна).

К

О

Н

У

С

III. Выбор второй тройки:

Вопросы:

1) Сколько здесь треугольников? (Ответ: 18.)

2) Сколько прямоугольников? (Ответ: 18.)

3) Проведите два отрезка так, чтобы получилось 5 квадратов.

Задание.

Как назвать четырехугольник, у которого две стороны параллельны, а две другие непараллельны? (Это слово часто употребляется в цирке).

Т

Р

А

П

Е

Ц

И

Я

IV. Выбор третьей тройки.

Вопросы.

1. Два прямоугольника имеют одну и ту же площадь. Длина первого прямоугольника равна 4 дм, а ширина 0,9 м. Чему равна длина второго прямоугольника, если его ширина 3 дм.

2. Найдите объем прямоугольного параллелепипеда, если длина его равна 1,2 м, ширина 0,5 м, а высота 0,3 м.

3. Из деревянного бруска, длина которого 8 см, ширина 0,6 дм и высота 4 см, вырезали куб с ребром 0,04 м. Чему равен объем оставшейся части бруска?

Задание.

Как называется прямая, которая с окружностью имеет одну общую точку.

К

А

С

А

Т

Е

Л

Ь

Н

А

Я

V. Игра со зрителями.

Вычислить площадь фигуры.

VI. Финал.

Как называется одна из сторон прямоугольного треугольника?

Г

И

П

О

Т

Е

Н

У

З

А

VII. Супер-игра.

Как называли куб или шестигранник в Древней Греции?

Г

Е

К

С

А

Э

Д

Р

VIII. Домашнее задание: № 1842, 1843, 1844. Повторить п. 23–29.

Урок № 160
Обыкновенная дробь

(урок самооценки знаний)

Оборудование: лист самооценки знаний.

Ход урока

I. Повторение и обобщение изученного материала.

Сценка. Заходят три девочки: на груди первой плакат с дробью , у второй – , а у третьей (девочек предварительно подготовить). «Здравствуйте, мы Обыкновенные Дроби. А сейчас мы проверим, что вы о нас знаете». Вперед выходит «Дробь » и задает вопросы.

1) Как называется число 2? Где записывается числитель?

2) Как называется число 5? Где записывается знаменатель?

3) Что показывает знаменатель? Что показывает числитель?

4) Что вы еще можете обо мне сказать? ( – правильная дробь (объяснить), её можно изображать на числовом луче (как?); дробь можно записать в виде частного (дробь меньше 1).

Выходит вперед «Дробь » (также предлагает вопросы классу: что еще можно сказать о дроби ?…), а потом задает вопрос: чем отличается дробь от дроби ? ( – правильная дробь, а – неправильная). Выходит «Дробь », и ученики делают вывод, что дробь тоже неправильная, и продолжается беседа о неправильных дробях.

II. Какие математические операции можно выполнить с обыкновенными дробями? (Сравнивать, складывать, вычитать) – повторить правила. Ученики оценивают.

Примечание: так как это урок самооценки знаний, то на каждый ряд раздать листки по форме:

№ п/п	Фамилия, имя учащегося	Теоретическая часть	Выделение целой части числа	Записать в виде неправильной дроби	Сложение и вычитание дробей	Итоговая оценка
1	Иванов С.	3	4	4	5	4
2	Петров Е.
3	Сидоров А.

III. Тренировочные упражнения.

1. Выделить целую часть:

а) из дробей: .

б) из дробной части: .

2. Записать в виде неправильной дроби смешанные числа: .

3. Записать числа в порядке убывания: .

4. Выполнить действия:

а) ; г) ;

б) ; д) ;

в) ; е) .

IV. Домашнее задание: № 1820, 1821, 1822, 1823. Повторить действия с десятичными дробями.

Урок № 161

Сложение, вычитание, умножение

и деление десятичных дробей

Оборудование: индивидуальные карточки.

Ход урока

I. Устные упражнения.

1. Правила выполнения действий с десятичными дробями повторяются, уточняются во время устных упражнений.

Вычислить:

а) 3 + 0,3 0,01 + 0,03 0,007 + 0,02 0,02 + 0,004

б) 3,75 – 2 6,5 – 0,4 15,8 – 3,4 3,25 – 2,1

в) 6  0,6 7  0,02 0,5  0,08 4,2  1,5 + 4,2  0,5 2  3,9  0,5 4  7,8  0,25

г) 24,6 : 3 6,8 : 2 0,08 : 2 2 : 0,2 2,4 : 1,2 0,8 : 0,02

2. Округлить число 37,2573 до тысячных, сотых, десятых, единиц.

3. Игра «Заполни клетку».

Учащиеся получают листочки, текст которых приведен в таблице.

Вариант I. Фамилия________		Вариант II. Фамилия________
1,4 + 0,6 = – 1,7 =  1,2 = : 9 = + 0,96 = – 0,2 =  0,5 = : 0,02 =		2,6 + 0,04 = – 2,8 =  1,8 = : 12 = + 0,97 = – 0,1 =  0,5 = : 0,15 =

Примечание: Правило заполнения клеток состоит в том, что ответ предыдущего действия ставится в первую клетку следующего.

II. Выполнение письменных упражнений.

1. № 1834 (д, е).

2. Самостоятельно № 1836 (а).

3. № 1835 (а), 1836 (а).

III. Итог урока.

Соревнование «Думай и соображай».

1. Какой знак можно поставить между числами 7 и 8, чтобы получившееся число было больше 7 и меньше 8?

2. Между числами 7,3 и 7,4 поставьте число, большее 7,3 и меньшее 7,4.

3. Даны числа: 0,3; 7,7; 0,125. Поставьте между ними такие знаки, чтобы в результате выполнения указанных вами действий получилась единица. (Ответ: (0,3 + 7,7)  0,125).

4. Найти устно значение выражения: (13 – 2,46 : 3,54)  (0,5 – ).

IV. Домашнее задание: № 1834 (а, б), 1835 (б), 1836 (б).

Урок № 162
Решение уравнений

Оборудование: ксерокопии текстов каждого варианта.

Ход урока

I. Проверка домашнего задания.

Выполнить тест.

Вариант I

1. Вычислите: 3,34 + 28,7.

1) 32,04; 2) 31,41; 3) 31,04; 4) 62,1.

2. Вычислите: 0,34  0,8.

1) 2,72; 2) 0,272; 3) 27,2; 4) 0,0272.

3. Вычислите: 20,4 : 0,8.

1) 25,5; 2) 2,55; 3) 0,255; 4) 255

4. Округлите 0,6539 до сотых.

1) 0,7; 2) 0,65; 3) 0,66; 4) 0,654.

5. Расположите в порядке убывания числа 3,78; 3,784; 3,7801.

1) 3,7801; 3,78; 3,784; 2) 3,784; 3,78; 3,7801;

3) 3,784; 3,7801; 3,78; 4) 3,78; 3,7801; 3,784.

6. Выразите в метрах 0,002 км.

1) 20 м; 2) 200 м; 3) 2 м; 4) 2000 м.

7. Найдите площадь квадрата, сторона которого равна 1,1 дм.

1) 4,4 дм²; 2) 1,21 дм²; 3) 2,2 дм²; 4) 121 дм².

8. Из чисел 1; ; 1,05; выберите наименьшее.

1) 1; 2) ; 3) 1,05; 4) .

Фамилия, имя____________________________ класс________
№ задания	1	2	3	4	5	6	7	8
№ ответа

Вариант II

1. Вычислите: 6,35 – 3,5.

1) 2,85; 2) 3,3; 3) 6; 4) 3,85.

2. Вычислите: 0,7  0,26.

1) 0,182; 2) 0,0182; 3) 1,82; 4) 18,2.

3. Представьте в виде десятичной дроби .

1) 0,725; 2) 0,28; 3) 0,028; 4) 2,8

4. Округлите 0,2518 до десятых.

1) 0,25; 2) 0,2; 3) 0,3; 4) 0,251.

5. Расположите в порядке возрастания числа 1,4302; 1,43; 1,437.

1) 1,437; 1,4302; 1,43; 2) 1,43; 1,4302; 1,437;

3) 1,437; 1,43; 1,4302; 4) 1,4302; 1,43; 1,437.

6. Выразите в тоннах 16 кг.

1) 0,16 т; 2) 0,00016 т; 3) 0,0016 т; 4) 0,016 т.

7. Найдите периметр квадрата, сторона которого равна 1,3 дм.

1) 16,9 дм; 2) 2,6 дм; 3) 5,2 дм; 4) 1,3 дм.

8. Из чисел 0,98; ; 1; выберите наибольшее.

1) 0,98; 2) ; 3) 1; 4) .

Фамилия, имя____________________________ класс________
№ задания	1	2	3	4	5	6	7	8
№ ответа

II. Устные упражнения.

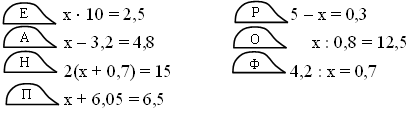
1. Решите уравнения. Заполните таблицу буквами, учитывая найденные ответы.

0,45	8	4,7	6	0,25	6,8	10

Что означает полученное слово?

(Ответ: Парфенон, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики, построен в 432 г. до н. э.)

2. Найдите корни уравнения:

х  1 = 0 0  х = 1 х – х = 0 х – х = 1

х – 10 = 10 х + 10 = 10 0  х = 0 0 + х = 10

х – 10 = 0 х : 10 = 10 0 : х = 1.

III. Тренировочные упражнения:

1. Решить уравнение:

а) (х – 5,6) : 12 = 3,7 б) (х + 2,1)  4 = 15,2 (2-я способами)

в) 3,4 – 9х = 1,6 г) 8,1 : х – 0,7 = 3

д) s : 2,3 = 4,6 е) 9,88 : (6,7 – х) = 2,6

ж) 6,7  (7,9 – у) = 28,81 з) 9,14z – (3,78z + 2,87z) = 12,45.

2. Решить самостоятельно:

а) 41 – 7,08у = 23,3 б) 4,6х + 3,8х –1,6 = 0,5

IV. Итог урока.

1. Можно привести высказывание Д. Чосера:

«Посредством уравнений, теорем

Он уйму всяких разрешил проблем:

И засуху предсказывал, и ливни.

Поистине его познанья дивны».

2. Решить уравнения:

а) 0,3х + 2,4 х = 270; б) 0,2  (4х + х) = 12; в) 2х + х + 0,6 = 4,2.

Используя найденные ответы, узнайте имена клоунов, если известно, что у Бима корень уравнения совпадает с ответом примера 40  1,25  0,8  2,5 =…, а у Бома корень уравнения наименьший. Третьего клоуна зовут Бум.

V. Домашнее задание: № 1817, 1828, 1876.

Урок № 163
Решение задач

Оборудование: плакат «Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!» (Д. Пойа).

Ход урока

I. Проверка домашнего задания.

1. Консультанты докладывают об итогах выполнения домашнего задания.

2. Соседи по парте обмениваются тетрадями, проверяют, исправляют и оценивают.

II. Устные упражнения.

1. Блиц-турнир.

1) В одной бригаде – х человек, а в другой – в 2 раза больше. Сколько человек в двух бригадах вместе?

2) Ботинки стоят х рублей, и они на 20 рублей дешевле шляпы.

а) Сколько стоит шляпа?

б) Сколько стоят ботинки и шляпа вместе?

3) Футбольный мяч стоит у рублей. Его цена была снижена на 25%. Какова новая цена мяча?

4) Чайный сервиз стоил 600 рублей. Через некоторое время цена его была снижена на х%. Сколько теперь стоит сервиз?

5) Свитер стоил у рублей. Его цена увеличилась наполовину. Сколько стал стоить свитер?

6) Рабочий делает х деталей за минуту. Сколько деталей он сделает за 1 час?

2. Переведите на математический язык каждое предложение и запишите его в виде равенства, если х – это количество яблок; у – количество груш.

1) Яблок в корзине столько же, сколько груш:_____________

2) Яблок на 6 меньше, чем груш: ________________________

3) Яблок в 3 раза больше, чем груш: _____________________

III. Выполнение письменных упражнений.

1. № 1729, 1731, 1778, 1780.

2. № 1784 (разобрать решение по готовому чертежу).

IV. Итог урока.

Самостоятельно решить № 1788.

V. Домашнее задание: № 16728, 1732, 1779.

Урок № 164
Решение задач

Ход урока

I. Самостоятельная работа.

На доске записан текст работы. Устно разбирается каждое задание, ученики вспоминают и обосновывают их теорией, а затем выполняют эту работу.

Задача № 1

Собственная скорость полета голубя 55 км/ч, а скорость ветра 5,5 км/ч. Голубь летит 0,2 ч против ветра и 0,4 ч по ветру. Какой путь пролетел голубь за все это время?

Задача № 2

Из имевшихся 15,4 рублей истратили 35%. Сколько рублей было истрачено?

Задача № 3

Турист прошел 12 км, что составило 30% всего намеченного пути. Сколько еще километров надо пройти туристу?

Задача № 4

Мама испекла 45 пирожных, из них со сладкой начинкой. Сколько пирожных со сладкой начинкой испекла мама?

Решить уравнение: 13,4х + 2,8 = 10,84.

II. Домашнее задание: № 1834 (б), 1785, 1839. Подготовиться к контрольной работе.

Урок № 165
Контрольная работа (итоговая)

Вариант I

1. Выполните действия: 3,8  0,15 – 1,04 : 2,6 + 0,83.

2. Имелось три куска материи. В первом куске было 19,4 м, во втором – на 5,8 больше, чем в первом, а в третьем куске было в 1,2 раза меньше, чем во втором. Сколько метров материи было в трех кусках вместе?

3. В книге 120 страниц. Рисунки занимают 35% книги. Сколько страниц занимают рисунки?

4. Два поля занимают площадь 156,8 га. Одно поле на 28,2 га больше другого. Найдите площадь каждого поля.

5. Начертите угол MKN, равный 140. Лучом КР разделите этот угол на два угла так, чтобы угол PKN был равен 55. Вычислите градусную меру угла MPK.

Вариант II

1. Выполните действия: 0,84 : 2,1 + 3,5  0,18 – 0,08.

2. В понедельник туристы прошли на лыжах 27,5 км, во вторник они прошли на 1,3 км больше, чем в понедельник. В среду туристы прошли в 1,2 раза меньше, чем во вторник. Сколько всего километров прошли туристы за эти три дня?

3. В книге 360 страниц. Повесть занимает 40% всей книги. Сколько страниц занимает повесть?

4. Два поля занимают площадь 79,9 га. Площадь первого поля в 2,4 раза больше второго. Какова площадь каждого поля?

5. Начертите угол МОК, равный 155. Лучом OD разделите этот угол так, чтобы получившийся угол MOD был равен 103. Вычислить градусную меру угла DOK.

Домашнее задание: решить другой вариант.

Урок № 44

Деление (п. 12)

Цели: научить формулировать ответ на вопрос: «Какое действие называется делением?», повторить, как называются числа при делении, выработать навык деления натуральных чисел.

Оборудование: на доске записать план изучения новой темы.

Ход урока

I. Устные упражнения.

1. Какой ряд быстрее сосчитает? (По количеству поднятых рук).

№ 493 (а, б).

2. № 497, 501 (вместо «подчеркнуть» употребите слово «назвать»).

II. Изучение нового материала (идет по вопросам плана).

1. Определение действия деления.

Решают задачу из текста и формулируют определение действия деления; читают несколько раз, 2–3 ученика формулируют это определение, и затем каждый своему соседу дает это определение.

2. Как называются числа при делении:

3. Что показывает частное? (Ответ сами ученики находят в учебнике).

4. Всегда ли возможно деление?

В тетради ученики записывают: Ни одно число нельзя делить на нуль.

5. Свойство единицы и нуля при делении.

а : 1 = а а : а = 1 0 : а = 0.

III. Закрепление.

1. Ученикам предлагается по учебнику найти ответы на вопросы плана.

2. № 473 (а–г) – комментирование с места.

3. Устно № 474 (а, б); 465; 467; 466.

4. № 472 (а, в, г, д, е, к).

5. Ответить на вопросы 1–4 к п. 12.

IV. Итог урока.

1. Найти значение выражения:

а) 285 : с, если с = 1; с = 3; с = 19.

б) d : 8, если d = 0; d = 96; d = 14.

2. Делимое в 14 раз больше частного. Можно ли найти делитель?

3. Каков правильный ответ?

В равенстве (а – 37) : (b +43) = 5 выражение (b + 43) является

а)частным; б) делителем; в) делимым.

IV. Домашнее задание: п. 12; № 517 (а, в); 518 (а, б), 515.

Заполнить таблицу.

а	b	a  b	a : b
42	6
	7	98
36		144
	5		15
63			21

Урок № 45

Деление (п. 12)

Цель: закрепить свойства деления.

Оборудование: пленки к кодоскопу по проверке домашней работы.

Ход урока

I. Проверка домашней работы (пленка к кодоскопу).

Учащиеся обменялись тетрадями и сверяют решения с экраном.

II. Устные упражнения (проверяют два ученика).

1. Продумайте , как проще выполнить умножение, и вычислите:

а) 19  2  5; б) 4  27  25; в) 13  6  50.

2. Угадайте корни уравнения: 15  а = 15 : а.

3. Из данных выражений составьте верные равенства:

Можно соединить графами.

4. Вставьте вместо кружков знаки арифметических действий и при необходимости скобки так, чтобы равенства были верными.

а) 100 o 8 o 6 = 52

б) 100 o 8 o 6 = 86

в) 100 o 8 o 6 = 98

III. Работа по теме урока.

1. Устно: № 474 (в, г); № 476; № 478 (а).

2. № 473 (д, е); 468, 469 (с комментированием).

№ 472 (б, з, и).

3. На повторение: № 499 (а); 500 (а); 506.

IV. Итог урока.

1. Составьте выражения для решения задачи.

а) Ракета пролетела за t мин 23380 км. С какой скоростью летела ракета?

б) d : 8, если d = 0; d = 96; d = 14.

2. Ракета пролетела S км со скоростью 540 км/мин.

Сколько минут летела ракета?

V. Домашнее задание: п. 12; № 517 (б, г), 518 (в), 514, 520.

Урок № 46
Деление (п. 12)

Цели: научить находить неизвестный множитель, делимое, делитель.

Оборудование: девиз урока «Чем больше я знаю, тем больше умею»; плакаты на каждый этап устных упражнений.

Ход урока

I. Устные упражнения (проводят ученики).

1. Первый ученик: «Отгадайте кроссворд».

1		6
	2
3
	4
5

По горизонтали:

1) Геометрическая фигура:

2) Символ, с помощью которого обозначают натуральные числа.

3) Инструмент для проведения отрезков.

4) Результат сложения.

5) Результат деления.

По вертикали: 6) Знак одного из действий.

2. Второй ученик предлагает задание. Вычислить:

3. Третий ученик: «Отгадайте корень уравнения».

а) z + z = z  z;

б) 16 : b = 16  b.

II. Работа по теме урока.

1. Устно № 475, 478 (б, в), 483.

2. Перед выполнением следующих заданий нужно задать вопросы:

а) Какое равенство называется уравнением?

б) Какое число называется корнем уравнения?

в) Что значит решить уравнение?

г) Как проверить, верно ли решено уравнение?

3. Решить: № 482 (а, б, г) – трое учеников одновременно решают у доски, затем класс проверяет их решение.

№ 485 (а, в); 487 (а).

4. На повторение: 499 (б), 501 (б).

Можно соединить графами.

III. Самостоятельная работа (по вариантам).

Вариант I	Вариант II
1) Найти частное:
а) 6237 : 9 б) 61596 : 87 в) 15792 : 329	а) 3424 : 8 б) 35088 : 86 в) 13608 : 243
2) Решить задачу из учебника
№ 512 (1)	№ 512 (2)
3) Частное меньше делимого в 12 раз. Можно ли найти делитель?	3) Произведение в 27 раз больше одного из двух множителей. Можно ли найти другой множитель?
4) Найти значение выражения:
а) 1326 : t, если t = 1; t = 6; t = 17. б) l : 15, если l = 0; l = 120; l = 210.	а) 1672 : р, если р = 1, р = 8, р = 19. б) k : 12, если k = 0; k = 108; k = 168.

IV. Домашнее задание: п. 12 (2-я часть); № 524 (а, б, в), 516, 519, 527 (а, д).

Урок № 47

Деление. Свойства деления (п. 12)

Цели: научить находить неизвестный множитель, делимое, делитель.

Ход урока

I. Проверка домашнего задания.

Консультанты докладывают о выполнении домашнего задания. Отмечают аккуратно выполненные работы.

II. Устные упражнения.

1. № 493 (д) (какой ряд быстрее сосчитает?).

2. № 495.

3. Вопросы по таблице домашнего задания.

а) Во сколько раз скорость автомобиля «Волга» больше скорости почтового голубя?

б) Во сколько раз скорость улитки меньше скорости пчелы?

в) На сколько км/ч скорость автомобиля «Ока» больше скорости верблюда?

III. Работа по теме урока.

1. № 464, 482 (б), 487 (в. г), 490, 488, 471 (а, б), 477, 486 (а, б).

2. На повторение: № 499 (в), 501, 502 (а, г).

IV. Итог урока.

1. № 485 (б, г).

2. Повторить теоретический материал п. 12.

V. Домашнее задание: п. 12; № 524 (г, д); 521, 523, 526 (а); 554 (б, е).

Урок № 48

Деление (п. 12)

Цели: вырабатывать навык деления натуральных чисел и применения свойств деления.

Оборудование: плакат для логического теста.

Ход урока

I. Устные упражнения.

1. Среди чисел 10; 20; 0 найти корень уравнения: у  10 = у : 10.

2. № 498.

3. Логический тест № 1. Анаграммой называется слово, в котором поменялись местами все или несколько букв в сравнении с исходным словом. Решить анаграмму – означает определить исходное слово.

Учитель вывешивает плакат с анаграммами.

Ответ: 1) прямая, луч, отрезок, периметр.

2) Лишнее слово «периметр», так как «периметр» – метрическая величина, а «прямая», «луч», «отрезок» – геометрические фигуры.

4. Логический тест № 2 (символико-графического типа).

II. Работа по теме урока.

1. Устно № 491, 478.

2. № 492 (а) – с разбором, № 492 (б) – самостоятельно, № 472.

3. На повторение: № 502, 511.

4. Самостоятельная работа обучающего характера.

(До начала урока пересадить учащихся так, чтобы в паре были «сильный» – «слабый»).

№ 472 (ж, л); 470; 487 (б, е); 479.

III. Домашнее задание.

п. 12; № 524 (е); 525; 522; 526 (б); 527 (в).

Урок № 49

Деление (п. 12)

Поэтическое звучание темы: Скорость, расстояние, время и таинственные отношения между ними

«Я люблю математику не только потому, что

она находит применение в технике, но и потому,

что она красива».

Петер Ропсе

Оборудование: тексты задач на плакатах; ксерокопии листов с домашним заданием; плакаты с высказываниями о задачах; костюм для дяди Степы-милиционера.

«Математическая задача иногда столь же увлекательна, как кроссворд, и напряженная умственная работа может быть столь же желанным упражнением, как стремительный теннис».

Д. Пойа

«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!»

Д. Пойа

«При решении задачи плохой план часто оказывается полезным, он может вести к лучшему плану».

Д. Пойа

«В задачах, которые ставит перед нами жизнь экзаменатором является сама природа».

У. Сойер

Ход урока

I. Устные упражнения.

На доске записаны краткие условия задач.

1. Из пунктов А и В навстречу друг другу выехали автомобиль со скоростью 60 км/ч и велосипедист со скоростью 15 км/ч. Встретятся ли автомобиль и велосипедист через 2 часа, если расстояние между пунктами 160 км? (Решить задачу двумя способами.)

2. Из лагеря геологоразведчиков выехал вездеход со скоростью 30 км/ч. Через 2 часа вслед за ним был послан другой вездеход. С какой скоростью он должен ехать, чтобы догнать первый через 4 часа после своего выхода? (Можно сделать чертеж к задаче.)

II. Работа по теме урока.

1. Повторить, как найти расстояние, время, скорость, и решить задачи.

2. По рисунку составить задачу на движение и решить ее.

3. Викторина (3 ученика).

а) Первый ученик: «Автомобиль «Москвич» за 3 часа может проехать 360 км. Бескрылая птица страус – лучший бегун в мире – развивает скорость до 120 км/ч. Сравните скорости автомобиля «Москвич» и страуса».

б) Второй ученик предлагает классу свою задачу.

«Скорость распространения света самая большая в природе – 300000 км/с. На Солнце произошла вспышка. Через какое время ее увидят на Земле, если расстояние от Земли до Солнца равно 150000000 км?

в) Третий ученик:

«Пройденный путь пешехода S, его скорость  и время движения t связаны соотношением S = t. Если пешеход за 4 часа прошел 24 км, то его скорость равна:

1) 12 км/ч; 2) 6 км/ч; 3) 96 км/ч; 4) 8 км/ч.

4. Решить олимпиадную задачу.

Из пунктов А и В, расстояние между которыми 100 км, со скоростями 20 км/ч и 30 км/ч выезжают навстречу друг другу два велосипедиста. Вместе с ними со скоростью 50 км/ч вылетают две мухи, летят до встречи, поворачивают и летят обратно до встречи с велосипедистами, снова поворачивают и т. д. Сколько километров пролетит каждая муха в направлении от А до В до того момента, когда велосипедисты встретятся?

Решение: Велосипедисты встретятся через 2 часа на расстоянии 40 км/ч от А. За это время каждая муха пролетела 100 км. Муха, вылетевшая из А, пролетела в направлении от А до В на 40 км больше, чем в обратном направлении, и поэтому от АВ она пролетела 70 км. Аналогично, вторая муха в направлении от А к В пролетела на 60 км меньше, чем в обратном, то есть 20 км.

Ответ: первая муха в направлении от А к В пролетела 70 км, вторая – 20 км.

5. Входит дядя Степа-милиционер и предлагает задачу из сборника задач по основам безопасности дорожного движения.

а) Ширина проезжей части дороги 15 м, зеленый сигнал светофора горит 20 секунд. С какой наименьшей скоростью может двигаться пешеход с момента загорания светофора, чтобы благополучно перейти дорогу?

Решение:

1) 15 м = 1500 см

2) 1500 : 20 = 75 см/с.

Ответ: пешеход может двигаться со скоростью 75 см/с.

б) Мотоциклист едет со скоростью 95 км/ч, а скорость велосипедиста на 76 км/ч меньше. Во сколько раз скорость мотоциклиста больше скорости велосипедиста? Кому из них легче остановиться?

Решение:

1) 95 – 76 = 19 км/ч

2) 95 : 19 = 5 раз.

Ответ: в 5 раз легче остановиться велосипедисту, так как при меньшей скорости короче тормозной путь.

III. Итог урока.

Отметить особо отличившихся учеников, если есть возможность, то наградить сувенирами.

VI. Домашнее задание: ученикам раздаются ксерокопии заданий.

1) Помогите французским девочкам.

Однажды Жанин и Моника поплыли по маленькой речке, отправившись из одного и того же места, но только Жанин поплыла против течения, а Моника поплыла по течению. Оказалось, что Моника забыла снять большие деревянные бусы. Через четверть часа девочки повернули обратно. Кто же из них подберет бусы Моники: сама Моника или Жанин? (Скорость обеих пловчих в неподвижной воде одинакова.)

2) Задача от дяди Степы.

Скорость легкового автомобиля 60 км/ч, а грузовика 15 км/ч. Во сколько раз скорость легкового автомобиля больше скорости грузовика? Какой автомобиль опаснее для школьника, начавшего движение по пешеходному переходу?

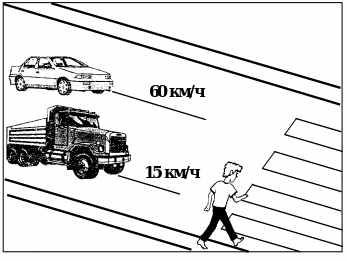
3) Задание от «Знающего человека». Заполнить таблицу.

Объект	Скорость 	Время t	Расстояние S
«Волга»	100 км/ч	5 ч
«Ока»	60 км/ч		420 км
«Москвич»		3 ч	240 км
Пчела	60 км/ч		180 км
Стрекоза		2 ч	200 км
Стриж	100 км/ч	4 ч
Меч-рыба	100 км/ч		300 км
Земля (вокруг Солнца)	30 км/ч	24 ч
Черепаха		6 мин	18 м
Улитка		7 ч	35 км
Верблюд	8 км/ч	5 ч
Почтовый голубь	50 км/ч		150 км

4) Составить по одной анаграмме.

Ответы для учителя.

Задача № 1

Скорости девушек относительно неподвижной воды одинакова. Но ведь по отношению к воде в реке бусы остаются неподвижными – они движутся в точности с такой же скоростью, что и вода (со скоростью течения). Пловчихи проплывают относительно воды одинаковое расстояние и по истечении получаса встречаются в том месте, где в этот момент находятся бусы. Таким образом, обе девушки могут подобрать бусы с равным основанием, так как встречаются в тот самый момент, когда подплывут бусы.

Задача № 2

Опаснее легковой автомобиль, так как у него скорость больше, кроме того, для водителя легкового автомобиля мальчик появится неожиданно, так как обзор будет закрыт грузовым автомобилем.

Урок № 50

Деление с остатком (п. 13)

Цели: объяснить учащимся, что деление натурального числа на другое нацело не всегда возможно; научить называть компоненты при делении с остатком и выполнять деление.

Оборудование: пленка для устных упражнений; кодоскоп.

Ход урока

I. Устные упражнения.

1. № 540 (а, б, в), 541 (а, б) – просвечивается на экран.

2. Учащиеся из своего домашнего задания задают анаграммы классу.

II. Изучение нового материала.

1. Ученики читают каждый абзац пункта, обсуждают и озаглавливают, в результате получается примерно такой конспект:

а) Деление одного натурального числа на другое нацело не всегда возможно;

б) При делении с остатком числа называются так.

в) Остаток всегда меньше делителя;

г) Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток.

23 = 4  5 + 3.

III. Закрепление.

1. Ответить на вопросы п. 13.

2. № 533 (д, б, в), 533 (а, е), 532 (3-я строка); 538.

3. На повторение. № 548 (3, 4) – самостоятельно.

IV. Итог урока.

Тест

1) При делении числа на 46 может получиться остаток:

а) 48; б) 45; в) 46; г) 47.

2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода?

а) в 2 раза; б) в 3 раза; в) в 4 раза; г) на 15 км/ч.

3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода?

а) в 4 раза; б) в 3 раза; в) в 2 раза.

V. Домашнее задание: п. 13 (уметь пересказать конспект); № 550 (а, в); 552; 553 (а); 555 (а, г), повторить п. 12.

Урок № 51
Деление с остатком (п. 13)

Цели: научить учащихся выполнять деление с остатком, решать задачи, используя действие деления.

Оборудование: билеты для проверки домашнего задания; плакат для устных упражнений и итогового теста; билеты с дополнительными вопросами.

Ход урока

I. Сообщается тема урока и цель, которая стоит перед учащимися. 10 человек вызываются к доске. Каждый из них вытаскивает себе билет. Пока класс выполняет устные упражнения, ученики готовятся к ответу, а потом отвечают.

Устные упражнения.

6 человек за первыми партами, 4 человека у доски обдумывают ответ на свои билеты.

1. Вывешивается плакат: «Восстановите цепочку вычислений».

2. Кто быстрее сосчитает?

60 – 22

: 2

+ 64

3. № 540 (д), 542.

Задания на билетах:

Билет № 1	Билет № 2
1) С помощью какого действия находят неизвестный множитель? 2) Вычисли: 1789405 : 2143.	1) Как называется число, которое делят? 2) Вычисли: 18291000 : 273.
Билет № 3	Билет № 4
1) Что такое делитель? 2) Частное 18252 : 36 равно: а) 57; б) 570; в) 4170; г) 507.	1) Как называется результат деления? 2) Значение выражения 972 : 9 : 3 равно: а) 6; б) 36; в) 324; г) 108.
Билет № 5	Билет № 6
1) Как найти неизвестное делимое? 2) Найди неполное частное и остаток: 1732 :41.	1) Как найти неизвестный делитель? 2) Найди неполное частное и остаток: 4183 : 53.
Билет № 7	Билет № 8
1) Чему равно а : 1, а : а, 0 : а? 2) Выполни действия: 782 : 26.	1) Может ли остаток быть больше делителя? Равным делителю? 2) Выполни действия: 312 : 19.
Билет № 9	Билет № 10
1) Как называются числа при делении с остатком? 2) Вырази делимое через неполное частное, делитель и остаток: 406 : 16.	1) Как найти делимое по неполному частному, делителю и остатку? 2) Вырази делимое через неполное частное, делитель и остаток: 810 : 25.

II. Тренировочные упражнения.

1. Вызываются к доске 4 ученика, решают предложенные задания, затем берут билет с дополнительным вопросом. После этого вставляется оценка.

1) № 533 (ж); 2) 533 (и);

3) 532 (1-я строка); 4) 532 (2-я строка).

2. № 529; 530.

3. Повторение: № 548 (1, 2); 549, 547.

III. Итог урока.

1. Придумать задачу, используя равенство: 2891 = 2  1000 + 891.

2. Тест (с международного конкурса «Кенгуру»).

Вывешивается плакат. Вдали мы видим силуэты замка. Какая из следующих линий не является частью этого силуэта?

III. Домашнее задание: п. 13, повторить п. 12; № 550 (б, г); 553 (б); 555 (в, г); 556 (а).

Урок № 52
Деление с остатком (п. 13)

Цели: научить учащихся выполнять деление с остатком, решать задачи, используя действие деления.

Оборудование: плакат на доске к № 526 (б).

Ход урока

I. Устные упражнения.

Одновременно трое учеников с текстами домашних заданий решают у доски. По окончании выполнения устных упражнений класс сверяет домашнее задание с доской.

1) Восстанови цепочку вычислений: (вывешивается плакат или откидная доска с № 539 (б). 2) 541 (в, г), 544.

1) № 550 (б, г), 553 (б), 555 (в, г). 2) № 556 (а).

II. Тренировочные упражнения.

1. Устно № 534, 537, 536 (а).

2. № 531, 535 (а) – у доски. № 535 (б) (комментирование с места).

3. Повторение: № 545, 546.

III. Домашнее задание: п. 11–12; № 553 (в), 551, 554, 556 (б).

Подготовиться к контрольной работе.

Урок № 53
Контрольная работа № 4 (п. 11–13)

Вариант I	Вариант II
1) Найдите значение выражения:
а) 8  99 – 816 : 8 б) 5713 : 197  (166 + 138)	а) 7  98 – 636 : 6 б) (167 + 238)  39 : 117
2) Упростите выражение:
а) m  75  6; б) 350  х  2	а) 35  с  8; б) у  450  4.
3) Решите уравнение:
а) 13590 : k = 45; б) 40 – 3х = 10.	а) 26520 : m = 65 б) 4z – 22 = 26.
4) Решите задачу с помощью уравнения:
Из 14 м2 материи сшили 2 пододеяльника. На каждый пододеяльник израсходовали 6 м2. Сколько квадратных метров материи осталось?	Туристы за 5 дней проплыли на байдарке 98 км. В первый день они проплыли 22 км. А в каждый из последующих дней они проплыли одно и то же расстояние. Найдите это расстояние.
5) Найдите корень уравнения и сделайте проверку.
5 – х  х = 1	х  х – 1 =15.

Домашнее задание. Решить другой вариант.

Урок № 54
Распределительное свойство

умножения (п. 14, ч. I)

Цели: научить формулировать и применять распределительное свойство умножения относительно сложения и вычитания.

Оборудование: плакат по теме с рис. 53.

Ход урока

I. Анализ контрольной работы.

а) Общий анализ контрольной работы.

б) Объяснение задания, с которым не справилось большинство учащихся.

в) Демонстрация лучших работ.

При проверке контрольной работы вести индивидуальный учет пробелов знаний и давать ученикам соответствующее задание.

II. Изучение нового материала.

1. Материал излагается в соответствии с учебником; учащимся предлагается вспомнить, что в учебнике отмечается двумя вертикальными чертами; они прочитывают несколько раз, запоминают, рассказывают друг другу, затем предлагается одному ученику на доске записать эти свойства.

2. Вспомнить переместительное и сочетательное свойства.

3. № 559 (а) – показать образец оформления.

4. Решить № 559 (д, б, е); 559 (в, и, г, к) – полусамостоятельно.

5. № 560 (а–г); 561 (б, г); 557, 558.

6. На повторение: № 585, 587 (а), 588.

III. Итог работы.

Чтобы учителю получить информацию о КПД урока, предложить учащимся письменно (на листочках) сформулировать свойство умножения и листочки потом собрать.

IV. Домашнее задание: п. 14 (1-я часть); № 609 (а), 610 (а, в), 611 (а, в), 625 (а).

Урок № 55
Упрощение выражений (п. 14)

Цели: научить применять свойства умножения при упрощении выражений.

Оборудование: плакат или пленка для кодоскопа (№ 577, 578).

Ход урока

I. Проверка домашнего задания.

Консультант докладывает о результатах выполнения домашнего задания; к тем номерам, которые вызвали затруднение у многих, дается пояснение.

II. Устные упражнения.

1. Повторение теоретического материала п. 14 (1-я часть).

2. № 590 (в, г), 591 (а).

3. На доске написать большую цифру «0».

Учитель: Что вы, ребята, об этом числе и цифре знаете? При сложении каких чисел может получиться «0»? В каких случаях получается нуль при вычитании, при умножении, при делении?

III. Изучение нового материала.

1. Вопрос классу: «Для чего мы изучали распределительное свойство умножения?». Далее учитель объясняет, как это свойство применяется для упрощения выражений.

Можно сделать в тетради такую запись:

IV. Закрепление.

1. Каким свойством умножения воспользуемся при выполнении № 559? Устно: № 559 (ж, з), 564, 575 (а, б).

2. № 561 (а, б), 560 (д, е) – Чем отличаются задания этих номеров? в) 550 (б, д, в, ж) – комментирование с места.

3. Вызываются 4 человека к доске.

1) № 568 (а); б) № 568 (в); в) № 568 (д); г) № 576 (а).

4. № 577 (решить уравнением и арифметически).

5. На повторение № 603, 601 (г, е) – самостоятельно.

V. Итог урока.

Тест

1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?

а) х; б) 2х; в) 3х; г) 4х.

2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе?

а) 4а; б) 6а; в) 2а + 4; г) а +4.

3) Даны два выражения: 9(856 + 342) и 9  856 + 8  342. Какое выражение больше?

а) равны; б) первое; в) второе.

VI. Домашнее задание. п. 14; № 609 (б, г); № 614 (а, б); 612, 613 (б, г); 625 (б). Повторить п. 11–13. Придумать частушки про «нуль». Вопросы из п. 11–14.

Урок № 56

Упрощение выражений (п. 14)

Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений.

Оборудование: ксерокопии к домашнему заданию.

Ход урока

I. Проверка домашнего задания (решение записано заранее).

Соседи по парте обмениваются тетрадями, сверяют решение с доской.

II. Устные упражнения.

591 (б, в); 592 (в, г); 572 (б, г).

III. Изучение нового материала.

1. На доске записано краткое условие № 578. Ученики под руководством учителя устно рассуждают, составляют уравнение, а затем открывают учебники, где предлагается правильное оформление решения; ученики записывают его в тетрадь.

2. № 565, 566 (б), 566 (а) – самостоятельно.

3. Три ученика у доски:

а) 568 (б); б) 568 (г); г) 568 (е).

4. № 579, 580.

5. На повторение № 607 (2).

IV. Итог урока.

«Математическая перестрелка».

Выбирается жюри из 3–5 человек.

Класс делится на две команды.

1) Конкурс частушек про «нуль» (было задано на дом).

2) Команды друг другу задают вопросы по п. 11–14, примеры для устного выполнения. Те, кто не смог ответить на вопрос, выбывают из игры.

Жюри подводит итоги.

V. Домашнее задание. п. 14. Заполнить таблицу (даются ксерокопии), № 614 (в, г); 616; 623; 625 (в).

Образец таблицы

Словесная запись	Символическая запись
1) а на 70 больше b	а – b = 70
2) b на 4 меньше а
3) а в 70 раз больше b
4) а меньше b на 37
5)	а = b + 17
6)	а = 17 b
7)	b = 17 а
8) Одно число больше другого на 7
9)	27 – х = 15
10) Если собственная скорость катера 42 км/ч, а скорость течения реки х км/ч, то скорость катера по течению реки равна
11) Сумма, затраченная на покупку 5 тетрадей по х рублей, у карандашей по 15 рублей и одного дневника по 33 рубля, равна

Урок № 57
Упрощение выражений (п. 14)

Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений.

Оборудование: карточки для устных упражнений.

Ход урока

I. Проверка домашнего задания.

1. Сверить с доской решение задачи № 623.

II. Устные упражнения.

№ 593 (а. б); 594 (а), 600.

Каждому ученику дается карточка, в которой нужно записать только ответ.

Фамилия, имя класс
№ п/п	Номер задания	Ответ
1.	№ 593 (а)
2.	№ 593 (б)
3.	№ 600
4.	№ 562 (д)
6.	№ 594

III. Изучение нового материала.

1. № 569 (а, в), 573 (а), 574 (а).

2. № 587, 586 – устно разобрать, а затем учащиеся решают самостоятельно, № 584.

3. На повторение по вариантам № 608 (1, 2).

IV. Итог урока. Разобрать решение домашней задачи № 621.

V. Домашнее задание. п. 14, повторить п. 1, 2; № 613 (а), 615, 621, 624.

Урок № 58
Упрощение выражений (п. 14)

Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений.

Оборудование: плакат с натуральными числами, магнитная доска, набор магнитов.

Ход урока

I. Проверка домашнего задания.

1. Задача № 621 (сравнить решение с доской).

2. Вопросы к п. 1, 2. Прочитать числа.

II. Устные упражнения.

1. № 590 (д); 593 (в); 594 (б).

2. Повторить свойства умножения.

III. Работа по теме урока.

1. № 567 (а, б); 567 (б, д); 572, 574 (г).

2. Самостоятельная работа.

Вариант I	Вариант II
№ 529 (б), 570 (в)	№ 529 (в), 570 (г)
Решить задачу:
Бронза состоит из 3 частей олова и 17 частей меди. Сколько олова в бронзовой детали, если масса детали 660 г?	Смесь, состоящая из 3 частей грузинского чая и 4 частей индийского чая, имеет массу 210 г. Сколько граммов грузинского чая в этой смеси?

IV. Итог урока. 1) Дать пояснение к задаче № 615.

2) Отгадать чайнворд (№ 625).

V. Домашнее задание. п. 14, повторить п. 3, 4; № 622, 617, 625 (г).

Урок № 59
Порядок выполнения действий (п. 15)

Цели: научить различать действия первой ступени и действия второй ступени, правильно выполнять порядок действий.

Оборудование: плакат для устного счета, магниты; плакат для развития внимания и памяти.

Ход урока

I. Устные упражнения.

1. Восстановить цепочку вычислений.

2. Вычислить устно:

15  4 25  3

+16 : 15

: 19 +29

–4 : 17

? ?

3. Упростите выражение: а) 2а + 612 + 7а + 324

б) 38 + 5а + 75 + 6а.

II. Изучение нового материала.

1.	Умножение, деление
Сложение, вычитание	2-я ступень
1-я ступень

2. Три правила выполнения действий (работа с учебником).

3. Рассмотреть примеры № 1–4.

4. Изменить порядок действий можно на основе свойств сложения, вычитания и умножения.

III. Закрепление.

1. Повторить теоретический материал по вопросам п. 15.

2. Решить у доски:

а) № 627 (а); б) 627 (в); в) 627 (д); г) 627 (и).

а) № 628 (а); б) 628 (г); в) 628 (д); г) 628 (в).

3. Самостоятельная работа обучающего характера.

№ 627 (е, з); 639 (а, д, ж); 642.

IV. Итог урока. Тренировка внимания.

Учитель показывает ребятам плакат и обращается к ним: «Внимательно посмотрите на плакат. Вам дается 1 секунда, после чего плакат будет убран, а вы должны сложить три числа, которые были на нем, и назвать сумму этих чисел».

Эксперимент заключается в том, что дана установка: назвать сумму трех чисел. А вопросы будут иметь другое содержание: какое число записано внутри квадрата, треугольника и круга.

V. Домашнее задание. п. 15 (до программ и команд); № 647 (а, б, ж, з), 648 (б, г), 650.

Урок № 60

Порядок выполнения действий (п. 15)

Цели: закрепить навык в выполнении порядка действий; научить составлять программу и схему программы вычислений.

Оборудование: ксерокопии тестов каждому ученику; таблица для ответов, калька.

Ход урока

I. Проверка домашнего задания.

Выполнить тест.

1) В выражении 200 + (20 –10 : 2)  8 последним выполняется действие: а) умножение; б) деление; в) вычитание; г) сложение.		1) В выражении 400 – (40 + 2  7) : 2 последним выполняется действие: а) умножение; б) сложение; в) деление; г) вычитание
2) В выражении 19  57 – 69 + 120 : 5 последним выполняется действие: а) сложение; б) вычитание; в) деление; г) умножение.		2) В выражении 740 – 600 : 15 + 7  33 последним выполняется действие: а) умножение; б) деление; в) вычитание; г) сложение.
3) Составьте выражение для решения задачи:
В классе 25 человек. После уроков 7 человек пошли домой, а остальные разбились поровну на три команды для игры. Сколько человек в каждой команде? а) 25 : 3 – 7; б) 25 – 7: 3; в) (25 –7) : 3; г) (25 – 3) : 7.	У Белоснежки и 7 гномов было 25 конфет. Белоснежка съела 4 конфеты, а остальные конфеты гномы разделили между собой поровну. Сколько конфет стало у каждого гнома? а) (25 – 4) : 7; б) (25 – 7) : 4 в) 25 – 4 : 7; г) 25 : 7 – 4.
4) Не производя вычислений определите, в каком из примеров указанный порядок действий приводит к неверному результату:

Таблица для заполнения.

Фамилия, имя___________________класс______					Оценка учителя
Номер задания	1	2	3	4
Правильный ответ

Калька прикрепляется к таблице скрепками, ученики пишут ответ на кальке, через кальку хорошо видна таблица. После проверки работы ученика скрепки удаляются, калька с записями открепляется от карточки и с выставленной оценкой возвращается ученику.

II. Устные упражнения.

1. Восстановите цепочку вычислений:

2. Кто быстрее сосчитает?

3. № 638 (а, в).

III. Изучение нового материала.

1. Изложение теоретического материала согласно учебнику: при разборе примера (можно взять для начала проще, чем в учебнике) соответственно чертится схема вычислений.

(68 – 15)  4 = 212

IV. Закрепление.

1. Каким правилам подчиняется порядок выполнения действий?

2. № 628 (б, е), 627 (б, г, и), 629, 631, 632 (а).

3. На повторение самостоятельно: 639 (з, к), 639 (б, м), 640.

V. Итог урока.

Тест

1) Значение числового выражения равно 100. Где нужно поставить скобки?

а) (140 : 4 + 3)  5; б) 140 : (4 + 3  5); в) 140 : (4 + 3)  5.

2) Дано выражение 157  18 – 57  18. Как нужно изменить порядок действий, чтобы удобно было считать?

а) 157 – 18  57; б) 158  18 – 57; в) 18  (157 – 57).

VI. Домашнее задание: п. 15; № 632, 631, 634 (а, в). Составить числовое выражение из 4 действий и схему к нему.

Урок № 61

Порядок выполнения действий (п. 15)

Цели: выработать навык правильного выполнения порядка действий, составления схем для вычисления значений числовых выражений.

Оборудование: карточки к самостоятельной работе.

Ход урока

I. Самостоятельная работа.

I вариант	II вариант
1) Выполните вычисления по схеме. Запишите выражение со скобками, соответствующее вычислительной схеме.
2) Составьте программу вычисления выражения:
(75  234 + 27  53)  2	(67  42 – 73  21) : 3

Запишите эту программу в виде схемы. Найдите значение выражения.

II. Устные упражнения.

№ 634 (д), 635, 637, 638 (б, г).

III. Работа по теме урока.

1. Что такое команда? (Последовательность выполнения действий в выражении). № 630 (ниже дан образец выполнения).

Числовое выражение: 381  29 – 7248 : 24.

Программа вычислений:

1) Умножить 381 на 29.

2) Разделить 7248 на 24.

3) От результата выполнения команды 1 отнять результат выполнения команды 2.

Схема выполнения.

2. № 632 (б).

3. Записать числовые выражения: № 646, 645 (домашние упражнения).

4. Выполнить № 627 (ж, к).

5. Самостоятельная работа по вариантам.

Вариант I: № 627 (л); 643 (1).

Вариант II: № 627 (м); 643 (2).

IV. Итог урока.

1. Ответить на вопросы к п. 15.

2. Соревнование соседей по парте: № 651.

V. Домашнее задание. п. 15 повторить 5, 6; № 644, 647 (в, г, д, е), 649. Составьте числовое выражение из 4 действий и схему к нему.

Урок № 62
Квадрат и куб числа (п. 16)

Цели: научить формулировать определение квадрата и куба числа, возводить числа в квадрат и куб, находить значения числовых выражений, содержащих вторую и третью степень натурального числа.

Оборудование: план изучения темы; плакаты для устных упражнений.

Ход урока

I. Изучение нового материала.

1. Сообщение темы урока.

2. Изучение соответствует плану (заранее написан на доске).

а) Что называется квадратом числа?

б) Таблица квадратов первых 10 натуральных чисел.

в) Что называется кубом числа?

г) Таблица кубов первых 10 натуральных чисел.

д) В каком порядке выполняются действия, если в числовое выражение входят квадраты и кубы чисел.

II. Закрепление.

1. № 655, 652 (составить таблицу и выучить).

2. № 657 (а, г, и).

3. Самостоятельно: № 657 (б, в).

4. На повторение: № 663. Девочки – № 665 (1), мальчики № 665 (2).

III. Устные упражнения.

1. 2³ – 4; 2) 5² + 2²; 3) 15² – 25.

2. Каков порядок действий: а) 160 + 37 – 20 + 5².

б) 90 – 60 : 15.

3. «Быстро сообрази».

Найдите математический термин из четырех букв, который служит окончанием слов:

Пери…, диа…, мано…

IV. Домашнее задание. п. 16; № 666, 671, 669, 673. Выучить таблицу квадратов (от 1 до 20) и кубов (от 1 до 7), повторить п. 7, 8.

Поставить скобки так, чтобы равенство было верным:

9664 : 32 – 2  195 – 37  5 = 3000.

Урок № 63
Квадрат и куб числа (п. 16)

Цели: выработать навык в вычислении значения выражения, содержащего квадрат и куб числа.

Оборудование: карточки, таблицы, калька для выполнения теста; набор карточек с числами от 1 до 20.

Ход урока

I. Выполнить тест.

I вариант	II вариант
1) Вычислите:
82 а) 64; б) 16; в) 2; г) 8.	103 а) 30; б) 3; в) 10; г) 1000.
2) Вычислите:
2  43 а) 24; б) 128; в) 512; г) 32.	3  52 а) 45; б) 30; в) 225; г) 75.
3) Упростите выражение:
11а – а – 21	11у + у + 3
а) 11а –2; б) 8а; в) 3а; в) 10 а – 2	а) 11у + 3; б) 12у + 3; в) 14у; г) 15у.
4) Найдите значение выражения:
у3 – 2 при у = 6. а) 16; б) 216; в) 214; д) 64.	х2 + 5 при х = 11 а) 126; б) 121; в) 27; г) 256.
5) Упростите выражение:
19 –(14 + с) а) 5с; б) 5 + с; в) 33 – с; г) 5 – с.	15 – (b + 2) а) 17 – b; б) 13 – b; в) 13b; г) 13 + b.
6) Для того чтобы разность 2874 945 12 была верной, вместо  надо поставить цифру: а) 9; б) 1; в) 0; г) 3.	6) Для того чтобы разность 3284 648 22 была верной, вместо  надо поставить цифру: а) 3; б) 7; в) 6; г) 4.

Таблица (с калькой) для заполнения результатов

Фамилия, имя _________________________класс_____							Оценка учителя
Номер задания	1	2	3	4	5	6
Ответ

II. Устные упражнения.

1. № 660 (а, в), 659 (г, д), 661.

2. Учитель показывает карточку и говорит «квадрат», ученики называют квадрат этого числа; аналогично повторяют кубы чисел.

3. Самостоятельно: № 657 (б, в).

4. На повторение: № 663. Девочки – № 665 (1), мальчики № 665 (2).

III. Тренировочные упражнения:

1. № 657 (д, з, е, ж), 658.

2. На повторение: № 664, 665 (з, и).

а) Вычислите (4³ – 7²)  84.

б) В каких случаях квадрат числа с равен частному с : с?

в) Вычислить устно и записать только ответ.

138 + 189 – 118 245  25  8

243 + 589 – 489 38  37 + 63  38

IV. Домашнее задание. п. 14–16; № 668,670, 672. Таблицы квадратов и кубов. Прочитать с. 117. Подготовиться к контрольной работе.

Урок № 64
Контрольная работа № 5

I вариант	II вариант
1) Найдите значение выражения:
а) (1142600 – 890778) : 74 + + 309  708. б) 132 + (52 – 49)3	а) 508  609 – (223136 + 18916) : 69 б) (44 – 38)2 + 132
2) Решите уравнение:
а) 4а + 8а = 204 б) 12у – 7у = 315	а) 5m + 6m = 231 б) 7х – 3х = 412
3) Решите задачу:
В двух пачках 168 тетрадей. В одной пачке в 3 раза меньше тетрадей, чем в другой. Сколько тетрадей в меньшей пачке?	В двух ящиках 75 кг яблок. В первом ящике в 2 раза больше яблок, чем во втором. Сколько яблок во втором ящике?
4) Упростите выражение
147 + 23х + 39х и найдите его значение при х = 3 и при х = 10	67х + 133 + 27х и найдите его значение при х = 4 и при х = 10
5) У Коли несколько трехкопеечных и несколько пятикопеечных монет. Всего 80 копеек. Трехкопеечных монет у него столько же, сколько и пятикопеечных. Сколько трехкопеечных монет у Коли?	5) У Сережи столько двухкопеечных монет, сколько и гривенников. Все монеты составляют сумму 60 копеек. Сколько двухкопеечных монет у Сережи?

II. Домашнее задание.

а) Решить другой вариант.

б) Познакомиться с п. 17.

Урок № 65

Формулы (п. 17)

Цели: научить определять, что такое формула, закрепить формулу пути (времени, скорости); учить вычислять по формуле.

Оборудование: карточки с индивидуальными заданиями по работе над ошибками; карточки с числом для № 668; раздаточный материал: прямоугольник и квадрат.

Ход урока

I. Анализ контрольной работы.

а) Общий анализ контрольной работы.

б) Объяснение заданий, с которыми не справились большинство учеников.

в) Демонстрация лучших работ.

Карточки с индивидуальными заданиями можно вложить в тетради с контрольной работой.

II. Устные упражнения.

1. № 686. (Учитель показывает карточку с числом, ученики находят квадраты чисел; аналогично находятся кубы чисел).

2. № 684 (а, б). (Выясняется, является ли полученный результат квадратом какого-либо числа?)

3. № 690, 692 – полуписьменно.

III. Изучение нового материала.

1. Работа по учебнику.

Запись в тетради: S – путь;  – скорость; t – время.

Формула пути:

2. По учебнику разбирается задача № 2.

t = S : .

3. Задача № 3

 = S : t.

4. Вспоминаются известные формулы.

Если а и b – стороны треугольника, Р – периметр, то Р = (а + b)  2.

5. Если а – стороны квадрата, то Р = 4а.

6. Если а – делимое, b – делитель, q – неполное частное и r – остаток, то а = b  q + r.

IV. Закрепление.

1. Что называется формулой?

2. Какое равенство называется формулой пути?

3. Что из этой формулы можно найти?

4. Какие еще формулы знаете?

5. На повторение: № 698 (устно), № 693 (а, в).

V. Итог урока. Практическая работа.

1) Измерить стороны прямоугольника и вычислить периметр.

2) Измерить сторону квадрата и вычислить периметр.

3) Сравнить полученные периметры.

VI. Домашнее задание. п. 17 (знать все изученные формулы и уметь их применять); № 701, 704, 707 (а, б); 708 (а).

Урок № 66
Формулы (п. 17)

Цели: научить читать и записывать формулы, производить вычисления по формулам.

Оборудование: «Ромашка с лепестками».

Ход урока

I. Проверка домашнего задания.

1. На доске написаны числа на шарах. Ответом к какому заданию они являются?

2. Какие единицы измерения должны быть у каждого числа?

3. Устно проверить решение № 704.

II. Устные упражнения.

1. Вычислить:

3. № 687, 691, 688 (а, б, в).

III. Тренировочные упражнения.

1. На доске прикреплена ромашка, на лепестках которой с обратной стороны записаны задания из № 675 (б), 676 (б), 679 (а), 679 (б), 678 (б), 677 (б), 683 и такое задание:

Выразите m из формулы а = 150 : m + 1 (всего 8 лепестков).

(4 человека вызываются к доске, после ответа одного вызываются по одному; можно включить дополнительный вопрос).

2. На повторение № 693 (б, г).

3. Самостоятельная работа на оценку:

Вариант I – № 699 (1); вычислить: (2³ + 5²)  3.

Вариант II – № 699 (2); вычислить: (6² + 3³) : 21

IV. Итог урока.

1. Повторить все формулы.

2. Какие формулы нужно использовать при решении домашнего задания № 702, 703.

V. Домашнее задание. п. 17, повторить п. 7, 8; № 702, 703, 707 (в, г), 708 (б).

Урок № 67
Площадь. Площадь прямоугольника (п. 18, ч. 1)

Цели: сформировать понятия квадратного сантиметра, площади фигуры; научить находить площадь прямоугольника, сложной фигуры, научить определять равные фигуры.

Оборудование: квадрат со стороной 1 см; раздаточный материал (по две фигуры, разбитые на кв. сантиметры); демонстрационные равные фигуры.

Ход урока

I. Проверка домашнего задания.

Консультанты до урока проверили домашние работы у учащихся и докладывают о их выполнении.

II. Устные упражнения.

1. Восстановить цепочку вычислений.

2. (70 : 5 +2)  4 – 64 Результат разделить на 11.

(48 : 4 – 2)  9 : 45 + 18 Результат возвести в квадрат.

3. Можно ли указать число, которое не является корнем уравнения:

а) х : х = 1; б) 0 : х = 0; в) m : 0 = 0; г)   1 = ?

4. Наименьшее четырехзначное число уменьшите на 100. Какой получится результат?

III. Изучение нового материала.

1) Что такое квадратный сантиметр?

2) Как найти площадь фигуры?

3) Рассмотреть примеры рис. 62, 63; найти площади фигур, лежащих на парте у учащихся.

4) S – площадь прямоугольника, а – длина, b – ширина.

S = аb.

5) Определение равных фигур (продемонстрировать).

6) Каковы площади равных фигур?

7) Чему равна площадь всей фигуры, если фигура разделена на части?

IV. Закрепление.

1. Устно № 709, 711, 712, 714.

2. № 716, 717.

3. На повторение: № 731, 732.

V. Итог урока.

Ответить на вопросы или найти в учебнике ответ на вопросы к п. 18.

VI. Домашнее задание. п. 18 (до площади квадрата); № 736, 741 (а), 744, 745.

Урок № 68

Квадрат. Формула площади квадрата (п. 18)

Цели: научить находить площадь треугольника, квадрата.

Оборудование: карточки для проверки домашнего задания; кодоскоп, пленки с устными упражнениями; пленки с рис. 64, 65; фигуры прямоугольника, квадрата, опорный конспект.

Ход урока

I. Проверка домашнего задания.

1. Проверить фронтально только ответы.

2. Площадь одного квадрата равна 1 см².

Какова площадь каждой фигуры.

Шесть человек за первыми партами выполняют работу по карточкам.

Карточки для учащихся.

Вариант I

1) Заполните таблицу, где а и b – стороны прямоугольника.

а	b	S	Р
32 см	7 см

2) Начертите две неравные фигуры, имеющие одинаковую площадь 3 см².

Вариант II

1) Заполните таблицу, где а и b – стороны прямоугольника.

а	b	S	Р
27 см	8 см

2) Начертите две неравные фигуры, имеющие одинаковую площадь 4 см².

II. Устные упражнения.

1. Найти значение выражения: 5² + 3²; (27 – 17)³; 1³ + 2³; 5²  2²; 0³ + 4².

2. № 724 (б), 723 (в, г, д), 726 (а, в).

III. Изучение нового материала.

1. Повторить по вопросам п. 18 (ч. 1).

2. На экран проецируется рис. 64 (работа с учебником).

3. Нахождение площади треугольника.

4. Определение квадрата.

5. Формула площади квадрата S = а².

6. Повторение единиц площади.

IV. Закрепление.

1. Устно № 710, 715, 719, 720.

2. № 713, 718.

3. На повторение: № 734 (по вариантам).

V. Итог урока.

Вывешивается опорный конспект по теме «Площадь».

Учитель показывает на какой-нибудь фрагмент, а ученики объясняют, комментируют.

VI. Домашнее задание. п. 18; 738, 739, 742 (б), 741 (а, б).

Урок № 69

Единицы измерения площади (п. 19)

Цели: научить учащихся отвечать на вопрос, какие единицы измерения площадей существуют, переводить одни единицы измерения площадей в другие, использовать знания при решении задач.

Оборудование: таблица единиц площади; индивидуальные задания для практической работы, кодоскоп, пленки с устными упражнениями.

Ход урока

I. Практическая работа.

Ученикам раздаются листы с чертежами прямоугольника и квадрата. Выполнить необходимые измерения и вычислить площадь и периметр фигур.

II. Устные упражнения.

№ 764 (а), 763 (а, б), 767.

III. Изучение нового материала.

1. Вспомнить, какие единицы измерения площади ученики знают.

2. Что такое квадратный миллиметр, квадратный сантиметр?

3. Что такое гектар?

4. Что за единица измерения площади 1 ар?

5. Что надо помнить при вычислении площадей?

6. Повторение единиц площади.

IV. Закрепление.

1. Вывешивается таблица, ученики изучают ее слева направо и наоборот.

2. № 748, 749, 751, 756 (а, б).

3. На повторение: № 583, 589.

V. Итог урока.

Ответить на вопросы п. 19.

VI. Домашнее задание. п. 19; 779, 781 (б), 784, 789 (а).

Урок № 70
Единицы измерения площади (п. 19)

Цели: научить учащихся отвечать на вопрос, какие единицы измерения площадей существуют, переводить одни единицы измерения площадей в другие, использовать знания при решении задач.

Оборудование: карточки для проверки домашнего задания.

Ход урока

I. Проверка домашнего задания.

1. За первые парты: 6 человек.

2. У доски: 4 человека.

3. Остальные выполняют устные упражнения.

За первыми партами:

Вариант I

1) Одна сторона прямоугольника равна 3 м, а другая на 2 м больше. Найдите площадь.

2) Найдите площадь треугольника ACD, если АВ = 3 см, AD = 6 см.

Вариант II

1) Одна сторона прямоугольника равна 4 м, а другая на 3-м больше. Найдите площадь.

2) Найдите площадь треугольника ABD, если АВ = AD = CD = ВС = 4 см.

Отвечающие у доски:

1. 1) Найдите площадь фигуры, считая, что площадь одной клетки равна 1 см².

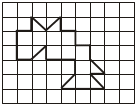
2) Как найти площадь всей фигуры, если известна площадь всех частей этой фигуры?

2. 1) Найдите периметр прямоугольника, площадь которого равна 30 см², а одна из его сторон – 5 см.

2) Что можно сказать о площадях равных фигур?

3. 1) Длина прямоугольника 32 см, а его ширина в 4 раза меньше. Чему равна площадь прямоугольника?

2) Что такое гектар?

4. 1) Найдите площадь всей фигуры, если даны следующие размеры: AD = АВ = 4 см, DN = 6 см.

2) Назовите в порядке возрастания единицы измерения площади.

II. Устные упражнения.

№ 554 (б), 765 (а, б, в), 772.

III. Тренировочные упражнения по теме урока.

1. № 747 (в, а), 750, 753, 756 (в), 760.

2. На повторение: № 769, 774, 776 (1, 2).

IV. Итог урока.

Вопросы к п. 19, таблица единиц площади.

V. Домашнее задание. п. 19; № 778, 780 (а), 785, 789 (б).

Урок № 71
Единицы измерения площади (п. 19)

Цели: научить учащихся отвечать на вопрос, какие единицы измерения площадей существуют, переводить одни единицы измерения площадей в другие, использовать знания при решении задач.

Оборудование: ксерокопии тестов.

Ход урока

I. Самостоятельная работа.

I вариант	II вариант
1. Найти площадь квадрата, сторона которого равна 11 см. 1) 44 см2; 2) 121 см2; 3) 22 см2; 4) 121 см.	1. Найти площадь квадрата, сторона которого равна 9 см. 1) 18 см2; 2) 81 см2; 3) 81 см; 4) 36 см2.
2. Найти площадь прямоугольника со сторонами 6 см и 4 см. 1) 24 см2; 2) 10 см2; 3) 20 см2; 4) 24 см.	2. Найти площадь прямоугольника со сторонами 3 см и 10 см. 1) 26 см2; 2) 30 см2; 3) 13 см2; 4) 30 см.
3. Найти периметр прямоугольника, одна из сторон которого равна 9 см, а его площадь – 36 см2. 1) 4 см; 2) 324 см; 3) 13 см; 26 см.	3. Найти периметр прямоугольника, площадь которого равна 40 см2, а одна из его сторон равна 5 см. 1) 26 см; 2) 8 см; 3) 13 см; 4) 200 см.
4. Найти площадь фигуры. 1) 14 см2; 2) 35 см2; 3) 26 см2; 4) 27 см2.	4. Найти площадь фигуры. 1) 48 см2; 2) 24 см2; 3) 33 см2; 4) 39 см2.
5. Найти площадь четырех-угольника ABCD. 1) 7 см2; 2) 14 см2; 3) 4 см2; 4) 9 см2.	5. Найти площадь четырёхугольника ABCD. 1) 7 см2; 2) 14 см2; 3) 4 см2; 4) 9 см2.

(Таблицы учета решений см. в ранее написанных разработках уроков.)

II. Устные упражнения.

№ 763 (в, г, д), 733, 768.

III. Тренировочные упражнения.

1. № 752 (с комментированием с места); № 756 (г), 755, 759.

2. Самостоятельная работа обучающего характера.

а) Площадь поля, имеющего форму прямоугольника, равна 54 га. Найдите ширину этого поля, если его длина 900 м.

б) Площадь земельного участка прямоугольной формы равна 12 а. Ширина участка 30 м. Найдите длину участка.

3. На повторение № 749 (а), 752, 756 (з, и).

IV. Итог урока.

«Догадайся».

Из 10 спичек составлен рисунок ключа (рис. 1). Переложите в нем 4 спички так, чтобы получить 3 квадрата

Ответ: Необходимо снять спички, изображающие кольцо ключа, и расположить их так, как показано на рис. 2

Рис. 1 Рис. 2

V. Домашнее задание. п. 19 повторить; № 770, 773, 777.

Урок № 72
Прямоугольный параллелепипед (п. 20)

Цели: сформировать понятие прямоугольного параллелепипеда, куба, научить находить ребра и грани, вычислять площадь поверхности прямоугольного параллелепипеда.

Оборудование: модели параллелепипеда, куба; плакат с числовым кроссвордом; индивидуальные листы с чертежом для итога урока.

Ход урока

I. Устные упражнения.

Отгадать числовой кроссворд (на столе листок для вычислений).

По горизонтали:

1) Наибольшее четырехзначное число; 2) 10³ – 1; 3) Число, показывающее, во сколько раз 3 км 500 м больше 250 м; 6) Наибольшее трехзначное число, записанное цифрами 5, 7 и 9; 7) 88 + 77 + 55 + 44; 9) 10  35  20 + 2148; 10) Длина всего отрезка, если отрезок разделен на части 12 см, 15 см, 7 см и 14 см; 11) Число минут в двух уроках по 40 минут плюс 10 минут; 13) Число, запись которого римскими цифрами выглядит так: LXIV; 14) Количество сотен в числе 10000; 15) Неизвестное слагаемое в равенстве 71 + х = 96; 17) Число, которое в виде суммы разрядных слагаемых выглядит так: 4  1000 + 3  10; 18) Число, которое в 3 раза больше числа 203; 19) Самолет пролетел 2100 км за 3 часа. Чему равна его средняя скорость?

По вертикали:

2) Количество сантиметров в 95 м 48 см; 3) Число, на 1 большее, чем 4²; 4) Число, которое в виде суммы разрядных слагаемых выглядит так: 4  1000 + 5  100 + 7  10 + 8; 5) Число, которое надо записать в рамочку: 1289071  тыс.; 7) 17²; 8) Сколько понадобится трехлитровых банок, чтобы разлить в них 86 л сока? 10) 200²; 12) Сумма числа 5134 и числа, записанного теми же цифрами, но в обратном порядке; 14) Наибольшее из чисел, которое можно подставить в неравенство: + 10 16) Неизвестный множитель в равенстве а  3 = 168; 17) Число 98 в 2 раза больше этого числа.

	1	2				3	4
5					6
7				8
				9		10
11			12
		13			14
15	16		17
	18				19

II. Изучение нового материала.

П. 20 – объяснение учителя с использованием моделей в соответствии с учебником.

III. Закрепление.

1. Ответ на вопросы п. 20.

2. № 791, 790, 792 (а), 953.

3. На повторение: № 805, 808 (самостоятельно)

IV. Итог урока.

Каждому выдается лист с заданием:

1) Рассмотрите рисунок и впишите пропущенные слова.

На рисунке изображен прямоугольный_____________________.

Точка К – его _________________________________________.

Отрезок АВ – его ______________________________________.

Прямоугольник АВКМ – его _____________________________.

2) Обведите равные ребра параллелепипеда одним цветом.

V. Домашнее задание. п. 20; № 811, 814, 816, 817 (а), 818.

Из плотной бумаги сделать прямоугольный параллелепипед, измерения которого равны:

Вариант I: а = 15 см, b = 12 см, с = 8 см.

Вариант II: а = 18 см, b = 10 см, с = 6 см.

Урок № 73
Объемы. Объем прямоугольного

параллелепипеда (п. 21)

Цели: сформировать понятия «больший объем», «меньший объем», «равенство объемов», научить вычислять объем прямоугольного параллелепипеда и куба.

Оборудование: два неравных сосуда, подкрашенная жидкость для сравнения объемов; два равных сосуда; модели кубического сантиметра, кубического дециметра; пленка, кодоскоп для выполнения устных упражнений.

Ход урока

I. Устные упражнения.

№ 830 (а), 829 (а, б), 831 (а, б).

II. Изучение нового материала.

План изложения нового материала.

1) Сравнение объемов.

2) Единицы измерения объемов.

3) Что такое 1 см³, 1 дм³?

4) Вывод правила вычисления объема прямоугольного параллелепипеда.

5) Формула объема прямоугольного параллелепипеда.

6) Как можно прочитать формулу V = abc.

7) Формула объема куба: V = а³.

III. Закрепление.

1. Ответить на вопросы п. 21 (вопросы 1–4).

2. Устно: № 814, 820 (а, в), 826, 823 – самостоятельно.

3. На повторение: № 814 (1, 2) – самостоятельно.

IV. Итог урока.

1. Предложить ученикам ответить на вопросы «Что нового узнали на уроке? Чему научились?».

2. А теперь я научу вас, как строить прямоугольный параллелепипед. Строим следующим образом:

V. Домашнее задание. п. 21; № 839, 841, 846 (а), 848 (а, в).

Практическая работа: сделать необходимые измерения и вычислить объем своей комнаты.

Урок № 74
Объемы. Соотношения между

единицами объема (п. 21)

Цели: научить переводить одни единицы объема в другие; закрепить навык вычисления объемов прямоугольного параллелепипеда и куба.

Оборудование: тесты, таблица ответов, калька для каждого ученика.

Ход урока

I. Проверка домашнего задания.

Выполнить тестирование по вариантам.

I вариант

1. В прямоугольном параллелепипеде ABCDMKSP равны ребра (см. рис.):

1) АМ и PS; 2) РМ и DC; 3) PD и ВК; 4) AB и KS.

2. В прямоугольном параллелепипеде ABCDMKSP равны грани (см. рис.):

1) MPDA и MPSK; 2) MABK и DPSC;

3) MABK и KBCS; 4) DPSC и MPDA.

3. Найдите объем прямоугольного параллелепипеда, длина которого 6 см, ширина – 2 см, а высота – 3см.

1) 12 см³; 2) 11 см³; 3) 36 см³; 4) 15 см³.

4. Найдите объем куба с ребром, равным 4 м.

1) 16 м³; 2) 12 м³; 3) 4 м³; 4) 64 м³.

Фамилия, имя класс
Номер задания	1	2	3	4
Номер ответа

Вариант II

1. В прямоугольном параллелепипеде ABCDMKSP равны ребра (см. рис.):

1) AD и PS; 2) МК и DC;

3) PD и ВС; 4) ВС и МК.

2. В прямоугольном параллелепипеде ABCDMKSP равны грани (см. рис.):

1) АМКВ и KBCS;

2) ADCB и BKSC;

3) MPDA и AMKB;

4) MPDA и KSCB.

3. Найдите объем прямоугольного параллелепипеда, длина которого равна 4 см, ширина – 2 см, а высота – 3 см.

1) 24 см³; 2) 8 см³; 3) 12 см³; 4) 9 см³.

4. Найдите объем куба с ребром, равным 5 дм.

1) 25 дм³; 2) 125 дм³; 3) 15 дм³; 4) 5 дм³.

Фамилия, имя класс
Номер задания	1	2	3	4
Номер ответа

II. Устные упражнения.

1. № 829 (в, г, д), 835, 832.

2. Решите анаграммы: ДВАКАТР, РОЗТЕКО, ТЕРГАК.

Объясните, что означает каждое слово.

Ответ: квадрат, отрезок, гектар.

III. Изучение нового материала.

План беседы.

1) Вспомнить, что такое 1 см³, 1 дм³.

2) Провести аналогию: 1 мм³, 1 м³, 1 км³.

3) 1 м³ = 10³ дм³ = 1000 дм³ = 1000 л.

4) 1 л = 1 дм³ = 1000 см³ 1 см³ = 1000 мм³

5) 1 км³ = 1 000 000 000 м³.

Примечание: во время объяснения пункты 3–5 не записывают; учитель обращает внимание на компактную запись единиц измерения объема, которая расположена на форзаце, её ученики записывают в тетради.

IV. Закрепление.

1. Назвать единицы измерения объема, начиная с самой малой.

2. Решить: № 825 (а, б, в), 820 (б, д), 824, 821, 828.

3. На повторение № 837 (самостоятельно).

V. Итог урока.

1. Повторить формулы объема.

2. Вопросы п. 21 (№ 5–8).

3. № 849.

VI. Домашнее задание. п. 21; № 840, 844, 846 (е, г), 848 (б, д), 834. Познакомиться с № 838.

Урок № 75
Объемы. Соотношения между

единицами объема (п. 21)

Цели: научить переводить одни единицы объема в другие; закрепить навык вычисления объемов прямоугольного параллелепипеда и куба.

Оборудование: на отдельном плакате каждая изученная формула; магнитная доска, набор магнитов.

Ход урока

I. Проверка домашнего задания.

Консультант докладывает о результатах выполнения домашней работы; если были затруднения, то учитель дает пояснения.

II. Устные упражнения.

1. Вспомнить все изученные формулы: S = t;  = S : t; t = S : ; Р = (а + b)  2; Р = 4а; а = bq + r; S = ab; S = a²; V = abc; V = a³.

2. Вычислить устно: 2³ + 3²; 3³ + 5²; 4³ + 6; 10³ – 10.

3. № 834.

III. Работа по теме урока.

1. № 820 (г), 825 (а, б, в) – с комментариями с места, № 822, 827.

2. Самостоятельная работа обучающего характера (ДМ, В. 2, 3).

Вариант I	Вариант II
1) Найти объем прямоугольного параллелепипеда, измерения которого равны:
24 м, 30 м и 450 дм.	26 дм, 25 дм и 4 м.
2) Объем физкультурного зала 1800 м3. Его высота 5 м. Какова площадь пола?	2) Объем ящика 13600 см3. Найдите площадь дна этого ящика, если его высота 16 см.
3) Чему равен объем куба, ребро которого 11 см?	3) Чему равен объем куба, ребро которого 12 см?
Дополнительное задание: Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 2 раза, но больше высоты на 4 см. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем.	Дополнительное задание: Длина прямоугольного параллелепипеда 24 см, и она больше ширины в 3 раза, а ширина на 3 см меньше высоты. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем.

IV. Итог урока.

Заполнить таблицы.

Скорость, v	Время, t	Расстояние, S		Длина: а	3 дм	16 см		5 см
18 км/ч	3 ч			Ширина: b	4 дм		20 дм
90 км/ч		450 км		Площадь: S		64 см2	80 дм2
	20 ч	600 км		Периметр: P				24

V. Домашнее задание. п. 21, повторить п. 17–19; № 845, 843, 846 (в), 848 (г, е). Подготовиться к контрольной работе.

Урок № 76

Контрольная работа № 6

Вариант I

1. Найдите по формуле S = t:

а) путь S, если t = 3 ч,  = 408 км/ч.

б) время t, если S = 7200 м,  = 800 м/мин.

2. Длина прямоугольного участка земли 650 м, а ширина на 50 м меньше. Найдите площадь участка и выразите ее в гектарах.

3. Длина прямоугольного параллелепипеда 45 см, ширина в 3 раза меньше длины, а высота на 2 см больше ширины. Найдите объем параллелепипеда.

4. Найдите значение выражения:

17040 – 69  238 – 43776 : 72.

5. Длина прямоугольника 84 см. Насколько уменьшится площадь прямоугольника, если его ширину уменьшить на 5 см?

Вариант II

1. Найдите по формуле S = t:

а) путь S, если t = 11 ч,  = 65 км/ч.

б) скорость , если S = 600 км, t = 50 с.

2. Ширина прямоугольного участка земли 600 м, а длина на 150 м больше. Найдите площадь участка и выразите ее в гектарах.

3. Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 3 раза. Высота параллелепипеда на 12 см меньше длины. Найдите объем параллелепипеда.

4. Найдите значение выражения:

350  92 – 66600 : 36 + 9670.

5. Ширина прямоугольника 44 см. Насколько уменьшится площадь этого прямоугольника, если его длину уменьшить на 5 см?

Домашнее задание.

Решить другой вариант. На урок принести циркуль, линейку.

Урок № 77
Окружность и круг

Цели: научить учащихся понимать, что такое окружность, круг, давать определения и строить радиус, диаметр, полукруг, полуокружность.

Оборудование: циркуль, линейка.

Ход урока

I. Анализ контрольной работы.

а) Общий анализ контрольной работы.

б) Объяснение заданий, с которыми не справились многие ученики.

в) Демонстрация лучших работ.

Карточки с индивидуальными заданиями для работы над ошибками ученики получают вместе с тетрадью для контрольных работ.

II. Устные упражнения.

1. Заполните клетки:

Является ли полученное число квадратом какого-либо числа?

Получившееся число возвести в куб и отнять 64.

2. № 861, 863.

III. Изучение нового материала.

Изложение учебного материала можно провести по плану:

1) Понятие окружности, определение круга, центра.

2) Свойства точек окружности.

3) Определение радиуса и диаметра.

4) Соотношение длин радиуса и диаметра.

5) Понятие полукруга, полуокружности, дуги, концов дуги.

IV. Закрепление.

1. Устно № 850.

2. Практическая работа № 851, 859, 855.

3. На повторение: № 868 (найти опечатку в учебнике: не сторона куба, а длина ребра куба).

№ 870, самостоятельно № 872 (1).

V. Итог урока.

Найти в тексте ответы на вопросы п. 22.

VI. Домашнее задание. п. 22 (то, что отмечено чертой); № 874, 875, 878 (а, в, д), 883 (а, в).

Урок № 78
Окружность, круг. Круговые шкалы

Цели: закрепить понятия окружности, круга, полукруга, полуокружности, дуги, навык построения этих фигур.

Оборудование: циркуль, линейка; модели шкал, расположенных по окружности и на дугах окружности; билеты с вопросами для проверки домашнего задания; плакат для устных упражнений, набор магнитов, магнитная доска.

Ход урока

I. Проверка домашнего задания.

Устные упражнения.

1. № 860 (в, г, д).

2. Плакат с заданием: укажите координаты точек А, В, С, D, если М(10). Сравните координаты точек В и С; С и D.

3. № 840.

Четыре человека у доски во время устных упражнений готовятся к ответу.

Содержание билетов.

Билет № 1

а) Рассказать, как строят окружность с помощью циркуля. Какой отрезок называется радиусом окружности? Построить окружность и радиус.

б) Перечислить свойства сложения.

Билет № 2

а) Какой отрезок называется диаметром окружности? Начертить его. Во сколько раз диаметр длиннее радиуса?

б) Как называются числа при сложении? Как найти неизвестное слагаемое (привести пример).

Билет № 3

а) Есть ли у окружности два радиуса различной длины? А два диаметра различной величины?

б) Как из числа отнять сумму двух чисел? Привести пример.

Билет № 4

а) Что называется кругом? Что такое окружность?

б) Как из суммы вычесть число? Привести примеры.

II. Изучение нового материала.

1. Сообщение темы урока.

2. Учащиеся читают соответствующий пункт учебника, а затем беседуют по содержанию пункта.

III. Закрепление.

1. Устно № 857, 858.

2. Письменно № 852, 854.

3. На повторение № 867, 871 (1) самостоятельно.

IV. Итог урока.

1. Узнайте, как называется наука, занимающаяся изучением происхождения слов. Для этого решите пример и заполните таблицу:

70	50	20	31	2	64	2	4	20	240

2. Верно ли высказывание: «Слово «цирк» и «циркуль» имеют одинаковое этимологическое происхождение». Для проверки дома воспользуйтесь этимологическим словарем.

V. Домашнее задание. п. 22, повторить п. 8, 9; № 876, 878, 880 (б, г, е), 883 (б, г).