СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Поурочные планы по математике 5 класс к книге Н.Я.Виленкина 2 четверть
Поурочные планы по математике 5 класс к книге Н.Я.Виленкина 2 четверть
Просмотр содержимого документа
«Поурочные планы по математике 5 класс к книге Н.Я.Виленкина 2 четверть»
Урок тема: Деление
Цели: научить формулировать ответ на вопрос: «Какое действие называется делением?», повторить, как называются числа при делении, выработать навык деления натуральных чисел.
Оборудование: на доске записать план изучения новой темы.
Ход урока
I. Устные упражнения.
1. Какой ряд быстрее сосчитает? (По количеству поднятых рук).
№ 493 (а, б).
2. № 497, 501 (вместо «подчеркнуть» употребите слово «назвать»).
II. Изучение нового материала (идет по вопросам плана).
1. Определение действия деления.
Решают задачу из текста и формулируют определение действия деления; читают несколько раз, 2–3 ученика формулируют это определение, и затем каждый своему соседу дает это определение.
2. Как называются числа при делении:

3. Что показывает частное? (Ответ сами ученики находят в учебнике).
4. Всегда ли возможно деление?
В тетради ученики записывают: Ни одно число нельзя делить на нуль.
5. Свойство единицы и нуля при делении.
а : 1 = а а : а = 1 0 : а = 0.
III. Закрепление.
1. Ученикам предлагается по учебнику найти ответы на вопросы плана.
2. № 473 (а–г) – комментирование с места.
3. Устно № 474 (а, б); 465; 467; 466.
4. № 472 (а, в, г, д, е, к).
5. Ответить на вопросы 1–4 к п. 12.
IV. Итог урока.
1. Найти значение выражения:
а) 285 : с, если с = 1; с = 3; с = 19.
б) d : 8, если d = 0; d = 96; d = 14.
2. Делимое в 14 раз больше частного. Можно ли найти делитель?
3. Каков правильный ответ?
В равенстве (а – 37) : (b +43) = 5 выражение (b + 43) является
а)частным; б) делителем; в) делимым.
IV. Домашнее задание: п. 12; № 517 (а, в); 518 (а, б), 515.
Урок тема: Деление
Цель: закрепить свойства деления.
Оборудование: пленки к кодоскопу по проверке домашней работы.
Ход урока
I. Проверка домашней работы (пленка к кодоскопу).
Учащиеся обменялись тетрадями и сверяют решения с экраном.
II. Устные упражнения (проверяют два ученика).
1. Продумайте , как проще выполнить умножение, и вычислите:
а) 19 2 5; б) 4 27 25; в) 13 6 50.
2. Угадайте корни уравнения: 15 а = 15 : а.
3. Из данных выражений составьте верные равенства:
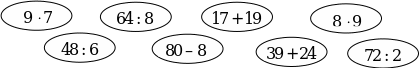
Можно соединить графами.
4. Вставьте вместо кружков знаки арифметических действий и при необходимости скобки так, чтобы равенства были верными.
а) 100 o 8 o 6 = 52
б) 100 o 8 o 6 = 86
в) 100 o 8 o 6 = 98
III. Работа по теме урока.
1. Устно: № 474 (в, г); № 476; № 478 (а).
2. № 473 (д, е); 468, 469 (с комментированием).
№ 472 (б, з, и).
3. На повторение: № 499 (а); 500 (а); 506.
IV. Итог урока.
1. Составьте выражения для решения задачи.
а) Ракета пролетела за t мин 23380 км. С какой скоростью летела ракета?
б) d : 8, если d = 0; d = 96; d = 14.
2. Ракета пролетела S км со скоростью 540 км/мин.
Сколько минут летела ракета?
V. Домашнее задание: п. 12; № 517 (б, г), 518 (в), 514, 520.
Урок тема:Деление
Цели: научить находить неизвестный множитель, делимое, делитель.
Оборудование: девиз урока «Чем больше я знаю, тем больше умею»; плакаты на каждый этап устных упражнений.
Ход урока
I. Устные упражнения ( презентация)
«Отгадайте корень уравнения».
а) z + z = z z;
б) 16 : b = 16 b.
II. Работа по теме урока.
1. Устно № 475, 478 (б, в), 483.
2. Перед выполнением следующих заданий нужно задать вопросы:
а) Какое равенство называется уравнением?
б) Какое число называется корнем уравнения?
в) Что значит решить уравнение?
г) Как проверить, верно ли решено уравнение?
3. Решить: № 482 (а, б, г) – трое учеников одновременно решают у доски, затем класс проверяет их решение.
№ 485 (а, в); 487 (а).
4. На повторение: 499 (б), 501 (б).
Можно соединить графами.
III. Самостоятельная работа (по вариантам).
| Вариант I | Вариант II |
| 1) Найти частное: | |
| а) 6237 : 9 б) 61596 : 87 в) 15792 : 329 | а) 3424 : 8 б) 35088 : 86 в) 13608 : 243 |
| 2) Решить задачу из учебника | |
| № 512 (1) | № 512 (2) |
| 3) Частное меньше делимого в 12 раз. Можно ли найти делитель? | 3) Произведение в 27 раз больше одного из двух множителей. Можно ли найти другой множитель? |
| 4) Найти значение выражения: | |
| а) 1326 : t, если t = 1; t = 6; t = 17. б) l : 15, если l = 0; l = 120; l = 210. | а) 1672 : р, если р = 1, р = 8, р = 19. б) k : 12, если k = 0; k = 108; k = 168. |
IV. Домашнее задание: п. 12 (2-я часть); № 524 (а, б, в), 516, 519, 527 (а, д).
Урок тема:Деление. Свойства деления
Цели: научить находить неизвестный множитель, делимое, делитель.
Ход урока
I. Проверка домашнего задания.
Консультанты докладывают о выполнении домашнего задания. Отмечают аккуратно выполненные работы.
II. Устные упражнения.
1. № 493 (д) (какой ряд быстрее сосчитает?).
2. № 495.
3. Вопросы по таблице домашнего задания.
а) Во сколько раз скорость автомобиля «Волга» больше скорости почтового голубя?
б) Во сколько раз скорость улитки меньше скорости пчелы?
в) На сколько км/ч скорость автомобиля «Ока» больше скорости верблюда?
III. Работа по теме урока.
1. № 464, 482 (б), 487 (в. г), 490, 488, 471 (а, б), 477, 486 (а, б).
2. На повторение: № 499 (в), 501, 502 (а, г).
IV. Итог урока.
1. № 485 (б, г).
2. Повторить теоретический материал п. 12.
V. Домашнее задание: п. 12; № 524 (г, д); 521, 523, 526 (а); 554 (б, е).
Урок тема: Деление
Цели: вырабатывать навык деления натуральных чисел и применения свойств деления.
Оборудование: плакат для логического теста.
Ход урока
I. Устные упражнения.
1. Среди чисел 10; 20; 0 найти корень уравнения: у 10 = у : 10.
2. № 498.
3. Логический тест № 1. Анаграммой называется слово, в котором поменялись местами все или несколько букв в сравнении с исходным словом. Решить анаграмму – означает определить исходное слово.
Учитель вывешивает плакат с анаграммами.

Ответ: 1) прямая, луч, отрезок, периметр.
2) Лишнее слово «периметр», так как «периметр» – метрическая величина, а «прямая», «луч», «отрезок» – геометрические фигуры.
4. Логический тест № 2 (символико-графического типа).

II. Работа по теме урока.
1. Устно № 491, 478.
2. № 492 (а) – с разбором, № 492 (б) – самостоятельно, № 472.
3. На повторение: № 502, 511.
4. Самостоятельная работа обучающего характера.
(До начала урока пересадить учащихся так, чтобы в паре были «сильный» – «слабый»).
№ 472 (ж, л); 470; 487 (б, е); 479.
III. Домашнее задание.
п. 12; № 524 (е); 525; 522; 526 (б); 527 (в).
Урок тема:Деление (п. 12)
Поэтическое звучание темы: Скорость, расстояние, время и таинственные отношения между ними
«Я люблю математику не только потому, что
она находит применение в технике, но и потому,
что она красива».
Петер Ропсе
Оборудование: тексты задач на плакатах; ксерокопии листов с домашним заданием; плакаты с высказываниями о задачах; костюм для дяди Степы-милиционера.
«Математическая задача иногда столь же увлекательна, как кроссворд, и напряженная умственная работа может быть столь же желанным упражнением, как стремительный теннис».
Д. Пойа
«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!»
Д. Пойа
«При решении задачи плохой план часто оказывается полезным, он может вести к лучшему плану».
Д. Пойа
«В задачах, которые ставит перед нами жизнь экзаменатором является сама природа».
У. Сойер
Ход урока
I. Устные упражнения.
На доске записаны краткие условия задач.
1. Из пунктов А и В навстречу друг другу выехали автомобиль со скоростью 60 км/ч и велосипедист со скоростью 15 км/ч. Встретятся ли автомобиль и велосипедист через 2 часа, если расстояние между пунктами 160 км? (Решить задачу двумя способами.)
2. Из лагеря геологоразведчиков выехал вездеход со скоростью 30 км/ч. Через 2 часа вслед за ним был послан другой вездеход. С какой скоростью он должен ехать, чтобы догнать первый через 4 часа после своего выхода? (Можно сделать чертеж к задаче.)
II. Работа по теме урока.
1. Повторить, как найти расстояние, время, скорость, и решить задачи.
2. По рисунку составить задачу на движение и решить ее.
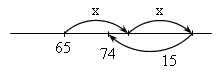
3. Викторина (3 ученика).
а) Первый ученик: «Автомобиль «Москвич» за 3 часа может проехать 360 км. Бескрылая птица страус – лучший бегун в мире – развивает скорость до 120 км/ч. Сравните скорости автомобиля «Москвич» и страуса».
б) Второй ученик предлагает классу свою задачу.
«Скорость распространения света самая большая в природе – 300000 км/с. На Солнце произошла вспышка. Через какое время ее увидят на Земле, если расстояние от Земли до Солнца равно 150000000 км?
в) Третий ученик:
«Пройденный путь пешехода S, его скорость и время движения t связаны соотношением S = t. Если пешеход за 4 часа прошел 24 км, то его скорость равна:
1) 12 км/ч; 2) 6 км/ч; 3) 96 км/ч; 4) 8 км/ч.
4. Решить олимпиадную задачу.
Из пунктов А и В, расстояние между которыми 100 км, со скоростями 20 км/ч и 30 км/ч выезжают навстречу друг другу два велосипедиста. Вместе с ними со скоростью 50 км/ч вылетают две мухи, летят до встречи, поворачивают и летят обратно до встречи с велосипедистами, снова поворачивают и т. д. Сколько километров пролетит каждая муха в направлении от А до В до того момента, когда велосипедисты встретятся?
Решение: Велосипедисты встретятся через 2 часа на расстоянии 40 км/ч от А. За это время каждая муха пролетела 100 км. Муха, вылетевшая из А, пролетела в направлении от А до В на 40 км больше, чем в обратном направлении, и поэтому от АВ она пролетела 70 км. Аналогично, вторая муха в направлении от А к В пролетела на 60 км меньше, чем в обратном, то есть 20 км.
Ответ: первая муха в направлении от А к В пролетела 70 км, вторая – 20 км.
5. Входит дядя Степа-милиционер и предлагает задачу из сборника задач по основам безопасности дорожного движения.
а) Ширина проезжей части дороги 15 м, зеленый сигнал светофора горит 20 секунд. С какой наименьшей скоростью может двигаться пешеход с момента загорания светофора, чтобы благополучно перейти дорогу?
Решение:
1) 15 м = 1500 см
2) 1500 : 20 = 75 см/с.
Ответ: пешеход может двигаться со скоростью 75 см/с.
б) Мотоциклист едет со скоростью 95 км/ч, а скорость велосипедиста на 76 км/ч меньше. Во сколько раз скорость мотоциклиста больше скорости велосипедиста? Кому из них легче остановиться?
Решение:
1) 95 – 76 = 19 км/ч
2) 95 : 19 = 5 раз.
Ответ: в 5 раз легче остановиться велосипедисту, так как при меньшей скорости короче тормозной путь.
III. Итог урока.
Отметить особо отличившихся учеников, если есть возможность, то наградить сувенирами.
VI. Домашнее задание: ученикам раздаются ксерокопии заданий.
1) Помогите французским девочкам.
Однажды Жанин и Моника поплыли по маленькой речке, отправившись из одного и того же места, но только Жанин поплыла против течения, а Моника поплыла по течению. Оказалось, что Моника забыла снять большие деревянные бусы. Через четверть часа девочки повернули обратно. Кто же из них подберет бусы Моники: сама Моника или Жанин? (Скорость обеих пловчих в неподвижной воде одинакова.)
2) Задача от дяди Степы.
Скорость легкового автомобиля 60 км/ч, а грузовика 15 км/ч. Во сколько раз скорость легкового автомобиля больше скорости грузовика? Какой автомобиль опаснее для школьника, начавшего движение по пешеходному переходу?
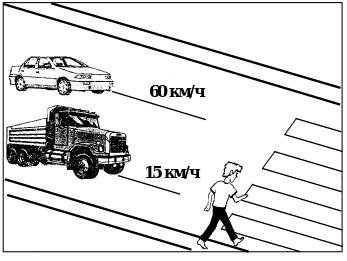
3) Задание от «Знающего человека». Заполнить таблицу.
| Объект | Скорость | Время t | Расстояние S |
| «Волга» | 100 км/ч | 5 ч |
|
| «Ока» | 60 км/ч |
| 420 км |
| «Москвич» |
| 3 ч | 240 км |
| Пчела | 60 км/ч |
| 180 км |
| Стрекоза |
| 2 ч | 200 км |
| Стриж | 100 км/ч | 4 ч |
|
| Меч-рыба | 100 км/ч |
| 300 км |
| Земля (вокруг Солнца) | 30 км/ч | 24 ч |
|
| Черепаха |
| 6 мин | 18 м |
| Улитка |
| 7 ч | 35 км |
| Верблюд | 8 км/ч | 5 ч |
|
| Почтовый голубь | 50 км/ч |
| 150 км |
4) Составить по одной анаграмме.
Ответы для учителя.
Задача № 1
Скорости девушек относительно неподвижной воды одинакова. Но ведь по отношению к воде в реке бусы остаются неподвижными – они движутся в точности с такой же скоростью, что и вода (со скоростью течения). Пловчихи проплывают относительно воды одинаковое расстояние и по истечении получаса встречаются в том месте, где в этот момент находятся бусы. Таким образом, обе девушки могут подобрать бусы с равным основанием, так как встречаются в тот самый момент, когда подплывут бусы.
Задача № 2
Опаснее легковой автомобиль, так как у него скорость больше, кроме того, для водителя легкового автомобиля мальчик появится неожиданно, так как обзор будет закрыт грузовым автомобилем.
Урок тема:Деление с остатком
Цели: объяснить учащимся, что деление натурального числа на другое нацело не всегда возможно; научить называть компоненты при делении с остатком и выполнять деление.
Оборудование: пленка для устных упражнений; презентация
Ход урока
I. Устные упражнения.
1. № 540 (а, б, в), 541 (а, б) – просвечивается на экран.
2. Учащиеся из своего домашнего задания задают анаграммы классу.
II. Изучение нового материала.
1. Ученики читают каждый абзац пункта, обсуждают и озаглавливают, в результате получается примерно такой конспект:
а) Деление одного натурального числа на другое нацело не всегда возможно;
б) При делении с остатком числа называются так.
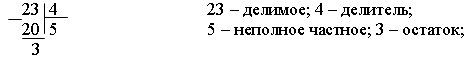
в) Остаток всегда меньше делителя;
г) Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток.
23 = 4 5 + 3.
III. Закрепление.
1. Ответить на вопросы п. 13.
2. № 533 (д, б, в), 533 (а, е), 532 (3-я строка); 538.
3. На повторение. № 548 (3, 4) – самостоятельно.
IV. Итог урока.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода?
а) в 2 раза; б) в 3 раза; в) в 4 раза; г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода?
а) в 4 раза; б) в 3 раза; в) в 2 раза.
V. Домашнее задание: п. 13 (уметь пересказать конспект); № 550 (а, в); 552; 553 (а); 555 (а, г), повторить п. 12.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза;б) в 3 раза; в) в 4 раза; г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода ? а) в 4 раза; б) в 3 раза; в) в 2 раза.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза; б) в 3 раза; в) в 4 раза; г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода? а) в 4 раза; б) в 3 раза; в) в 2 раза.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза; б) в 3 раза; в) в 4 раза;г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода? а) в 4 раза; б) в 3 раза; в) в 2 раза.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза; б) в 3 раза; в) в 4 раза;г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода? а) в 4 раза; б) в 3 раза; в) в 2 раза.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза; б) в 3 раза; в) в 4 раза;г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода? а) в 4 раза; б) в 3 раза; в) в 2 раза.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза; б) в 3 раза; в) в 4 раза; г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода? а) в 4 раза; б) в 3 раза; в) в 2 раза.
Тест
1) При делении числа на 46 может получиться остаток:
а) 48; б) 45; в) 46; г) 47.
2) Скорость пешехода 5 км/ч, а скорость велосипедиста 20 км/ч. Во сколько раз скорость велосипедиста больше скорости пешехода? а) в 2 раза; б) в 3 раза;в) в 4 раза; г) на 15 км/ч.
3) За 3 часа теплоход проплыл 105 км, а поезд за 2 часа проехал 110 км. Во сколько раз скорость поезда больше скорости теплохода? а) в 4 раза; б) в 3 раза; в) в 2 раза.
Урок тема: Деление с остатком
Цели: научить учащихся выполнять деление с остатком, решать задачи, используя действие деления.
Оборудование: билеты для проверки домашнего задания; презентация для устных упражнений и итогового теста; билеты с дополнительными вопросами.
Ход урока
I. Устные упражнения. (презентация)
Задания на билетах:
| Билет № 1 | Билет № 2 |
| 1) С помощью какого действия находят неизвестный множитель? 2) Вычисли: 1789405 : 2143. | 1) Как называется число, которое делят? 2) Вычисли: 18291000 : 273. |
| Билет № 3 | Билет № 4 |
| 1) Что такое делитель? 2) Частное 18252 : 36 равно: а) 57; б) 570; в) 4170; г) 507. | 1) Как называется результат деления? 2) Значение выражения 972 : 9 : 3 равно: а) 6; б) 36; в) 324; г) 108. |
| Билет № 5 | Билет № 6 |
| 1) Как найти неизвестное делимое? 2) Найди неполное частное и остаток: 1732 :41. | 1) Как найти неизвестный делитель? 2) Найди неполное частное и остаток: 4183 : 53. |
| Билет № 7 | Билет № 8 |
| 1) Чему равно а : 1, а : а, 0 : а? 2) Выполни действия: 782 : 26. | 1) Может ли остаток быть больше делителя? Равным делителю? 2) Выполни действия: 312 : 19. |
| Билет № 9 | Билет № 10 |
| 1) Как называются числа при делении с остатком? 2) Вырази делимое через неполное частное, делитель и остаток: 406 : 16. | 1) Как найти делимое по неполному частному, делителю и остатку? 2) Вырази делимое через неполное частное, делитель и остаток: 810 : 25. |
II. Тренировочные упражнения.
1) № 533 (ж); 2) 533 (и);
3) 532 (1-я строка); 4) 532 (2-я строка).
2. № 529; 530.
3. Повторение: № 548 (1, 2); 549, 547.
III. Итог урока.
III. Домашнее задание: п. 13, повторить п. 12; № 550 (б, г); 553 (б); 555 (в, г); 556 (а).
| Билет № 1 | Билет № 2 |
| 1) С помощью какого действия находят неизвестный множитель? 2) Вычисли: 1789405 : 2143. | 1) Как называется число, которое делят? 2) Вычисли: 18291000 : 273. |
| Билет № 3 | Билет № 4 |
| 1) Что такое делитель? 2) Частное 18252 : 36 равно: а) 57; б) 570; в) 4170; г) 507. | 1) Как называется результат деления? 2) Значение выражения 972 : 9 : 3 равно: а) 6; б) 36; в) 324; г) 108. |
| Билет № 5 | Билет № 6 |
| 1) Как найти неизвестное делимое? 2) Найди неполное частное и остаток: 1732 :41. | 1) Как найти неизвестный делитель? 2) Найди неполное частное и остаток: 4183 : 53. |
| Билет № 7 | Билет № 8 |
| 1) Чему равно а : 1, а : а, 0 : а? 2) Выполни действия: 782 : 26. | 1) Может ли остаток быть больше делителя? Равным делителю? 2) Выполни действия: 312 : 19. |
| Билет № 9 | Билет № 10 |
| 1) Как называются числа при делении с остатком? 2) Вырази делимое через неполное частное, делитель и остаток: 406 : 16. | 1) Как найти делимое по неполному частному, делителю и остатку? 2) Вырази делимое через неполное частное, делитель и остаток: 810 : 25. |
Урок тема:Деление с остатком
Цели: научить учащихся выполнять деление с остатком, решать задачи, используя действие деления.
Оборудование: презентация
Ход урока
I. Устные упражнения.презентация
II. Тренировочные упражнения.
1. Устно № 534, 537, 536 (а).
2. № 531, 535 (а) – у доски. № 535 (б) (комментирование с места).
3. Повторение: № 545, 546.
III. Домашнее задание: п. 11–12; № 553 (в), 551, 554, 556 (б).
Подготовиться к контрольной работе.
Урок Контрольная работа №4 по теме: «Умножение и деление натуральных чисел»
Вариант 1
1.Выполните действия:
а) 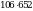 ; б)
; б) 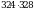 ;
;
в) 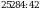 ; г)
; г) 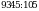 .
.
3.Выполните действия: а) 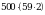 ; б)
; б) 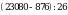 .
.
4.В магазин привезли 6 ящиков с красками. В каждом ящике 68 коробок, а в каждой коробке 16 тюбиков с красками. Сколько тюбиков привезли в магазин?
5.Решите уравнение: 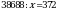 .
.
Вариант 2
1.Выполните действия:
а) 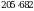 ; б)
; б) 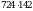 ;
;
в) 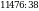 ; г)
; г) 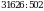 .
.
2.Выполните действия: а) 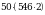 ; б)
; б) 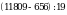 .
.
3. За год завод изготовил 4032 станка. Сколько станков в среднем изготавливал завод ежедневно, если в каждым месяце было 24 рабочих дня.
4. Решите уравнение: 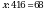 .
.
Вариант 1
1.Выполните действия:
а) 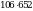 ; б)
; б) 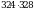 ;
;
в) 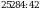 ; г)
; г) 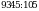 .
.
2.Выполните действия: а) 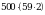 ; б)
; б) 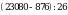 .
.
3.В магазин привезли 6 ящиков с красками. В каждом ящике 68 коробок, а в каждой коробке 16 тюбиков с красками. Сколько тюбиков привезли в магазин?
4.Решите уравнение: 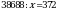 .
.
Вариант 2
1.Выполните действия:
а) 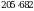 ; б)
; б) 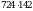 ;
;
в) 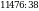 ; г)
; г) 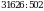 .
.
2.Выполните действия: а) 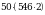 ; б)
; б) 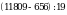 .
.
3. За год завод изготовил 4032 станка. Сколько станков в среднем изготавливал завод ежедневно, если в каждым месяце было 24 рабочих дня.
4. Решите уравнение: 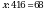 .
.
Вариант 1
1.Выполните действия:
а) 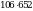 ; б)
; б) 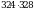 ;
;
в) 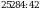 ; г)
; г) 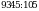 .
.
2,.Выполните действия: а) 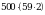 ; б)
; б) 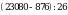 .
.
3.В магазин привезли 6 ящиков с красками. В каждом ящике 68 коробок, а в каждой коробке 16 тюбиков с красками. Сколько тюбиков привезли в магазин?
4.Решите уравнение: 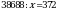 .
.
Урок тема:Распределительное свойство умножения
Цели: научить формулировать и применять распределительное свойство умножения относительно сложения и вычитания.
Оборудование: презентация
Ход урока
I. Анализ контрольной работы.
а) Общий анализ контрольной работы.
б) Объяснение задания, с которым не справилось большинство учащихся.
в) Демонстрация лучших работ.
При проверке контрольной работы вести индивидуальный учет пробелов знаний и давать ученикам соответствующее задание.
II. Изучение нового материала. (Презентация)
1. Материал излагается в соответствии с учебником; учащимся предлагается вспомнить, что в учебнике отмечается двумя вертикальными чертами; они прочитывают несколько раз, запоминают, рассказывают друг другу, затем предлагается одному ученику на доске записать эти свойства.
2. Вспомнить переместительное и сочетательное свойства.
3. № 559 (а) – показать образец оформления.
4. Решить № 559 (д, б, е); 559 (в, и, г, к) – полусамостоятельно.
5. № 560 (а–г); 561 (б, г); 557, 558.
6. На повторение: № 585, 587 (а), 588.
III. Итог работы.
Чтобы учителю получить информацию о КПД урока, предложить учащимся письменно (на листочках) сформулировать свойство умножения и листочки потом собрать.
IV. Домашнее задание: п. 14 (1-я часть); № 609 (а), 610 (а, в), 611 (а, в), 625 (а).
Урок тема: Упрощение выражений
Цели: научить применять свойства умножения при упрощении выражений.
Оборудование: презентация
Ход урока
I. Проверка домашнего задания.
Консультант докладывает о результатах выполнения домашнего задания; к тем номерам, которые вызвали затруднение у многих, дается пояснение.
II. Устные упражнения. (Презентация)
1. Повторение теоретического материала п. 14 (1-я часть).
2. № 590 (в, г), 591 (а).
3. На доске написать большую цифру «0».
Учитель: Что вы, ребята, об этом числе и цифре знаете? При сложении каких чисел может получиться «0»? В каких случаях получается нуль при вычитании, при умножении, при делении?
III. Изучение нового материала.
1. Вопрос классу: «Для чего мы изучали распределительное свойство умножения?». Далее учитель объясняет, как это свойство применяется для упрощения выражений.
Можно сделать в тетради такую запись:
![]()
IV. Закрепление.
1. Каким свойством умножения воспользуемся при выполнении № 559? Устно: № 559 (ж, з), 564, 575 (а, б).
2. № 561 (а, б), 560 (д, е) – Чем отличаются задания этих номеров? в) 550 (б, д, в, ж) – комментирование с места.
3. Вызываются 4 человека к доске.
1) № 568 (а); б) № 568 (в); в) № 568 (д); г) № 576 (а).
4. № 577 (решить уравнением и арифметически).
5. На повторение № 603, 601 (г, е) – самостоятельно.
V. Итог урока.
Тест
1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе?
а) 4а; б) 6а; в) 2а + 4; г) а +4.
3) Даны два выражения: 9(856 + 342) и 9 856 + 8 342. Какое выражение больше?
а) равны; б) первое; в) второе.
VI. Домашнее задание. п. 14; № 609 (б, г); № 614 (а, б); 612, 613 (б, г); 625 (б). Повторить п. 11–13. Придумать частушки про «нуль». Вопросы из п. 11–14.
Тест
1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе?
а) 4а; б) 6а; в) 2а + 4; г) а +4.
3) Даны два выражения: 9(856 + 342) и 9 856 + 8 342. Какое выражение больше?
а) равны; б) первое; в) второе.
Тест
1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе?
а) 4а; б) 6а; в) 2а + 4; г) а +4.
3) Даны два выражения: 9(856 + 342) и 9 856 + 8 342. Какое выражение больше?
а) равны; б) первое; в) второе.
Тест
1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе?
а) 4а; б) 6а; в) 2а + 4; г) а +4.
3) Даны два выражения: 9(856 + 342) и 9 856 + 8 342. Какое выражение больше?
а) равны; б) первое; в) второе.
Тест
1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе?
а) 4а; б) 6а; в) 2а + 4; г) а +4.
3) Даны два выражения: 9(856 + 342) и 9 856 + 8 342. Какое выражение больше?
а) равны; б) первое; в) второе.
Тест
1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе?
а) 4а; б) 6а; в) 2а + 4; г) а +4.
3) Даны два выражения: 9(856 + 342) и 9 856 + 8 342. Какое выражение больше?
а) равны; б) первое; в) второе.
Тест
1) В одном мешке было х кг картофеля, а в другом в 2 раза больше. Сколько килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
2) Вася решил а задач, а Миша – на 4 задачи больше. Сколько задач решили Вася и Миша вместе? а) 4а; б) 6а; в) 2а + 4; г) а +4.
3) Даны два выражения: 9(856 + 342) и 9 856 + 8 342. Какое выражение больше?
а) равны; б) первое; в) второе.
Урок тема:Упрощение выражений
Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений.
Оборудование: Презентация.
Ход урока
I. Проверка домашнего задания
II. Устные упражнения. Презентация
591 (б, в); 592 (в, г); 572 (б, г).
III. Изучение нового материала.
1. На доске записано краткое условие № 578. Ученики под руководством учителя устно рассуждают, составляют уравнение, а затем открывают учебники, где предлагается правильное оформление решения; ученики записывают его в тетрадь.
2. № 565, 566 (б), 566 (а) – самостоятельно.
3. Три ученика у доски:
а) 568 (б); б) 568 (г); г) 568 (е).
4. № 579, 580.
5. На повторение № 607 (2).
IV. Итог урока.
«Математическая перестрелка».
Выбирается жюри из 3–5 человек.
Класс делится на две команды.
1) Конкурс частушек про «нуль» (было задано на дом).
2) Команды друг другу задают вопросы по п. 11–14, примеры для устного выполнения. Те, кто не смог ответить на вопрос, выбывают из игры.
Жюри подводит итоги.
V. Домашнее задание. п. 14. № 614 (в, г); 616; 623; 625 (в).
Урок Тема: Упрощение выражений
Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений.
Оборудование: карточки для устных упражнений.
Ход урока
I. Проверка домашнего задания.
1. Сверить с доской решение задачи № 623.
II. Устные упражнения.
№ 593 (а. б); 594 (а), 600.
Каждому ученику дается карточка, в которой нужно записать только ответ.
| Фамилия, имя класс | ||
| № п/п | Номер задания | Ответ |
| 1. | № 593 (а) |
|
| 2. | № 593 (б) |
|
| 3. | № 600 |
|
| 4. | № 562 (д) |
|
| 6. | № 594 |
|
III. Изучение нового материала.
1. № 569 (а, в), 573 (а), 574 (а).
2. № 587, 586 – устно разобрать, а затем учащиеся решают самостоятельно, № 584.
3. На повторение по вариантам № 608 (1, 2).
IV. Итог урока. Разобрать решение домашней задачи № 621.
V. Домашнее задание. п. 14, повторить п. 1, 2; № 613 (а), 615, 621, 624.
Урок тема: Упрощение выражений
Цели: выработать навык в применении свойств умножения при упрощении выражений и при решении уравнений.
Оборудование: плакат с натуральными числами, магнитная доска, набор магнитов.
Ход урока
I. Проверка домашнего задания.
1. Задача № 621 (сравнить решение с доской).
2. Вопросы к п. 1, 2. Прочитать числа.
II. Устные упражнения.
1. № 590 (д); 593 (в); 594 (б).
2. Повторить свойства умножения.
III. Работа по теме урока.
1. № 567 (а, б); 567 (б, д); 572, 574 (г).
2. Самостоятельная работа.
| Вариант I | Вариант II |
| № 529 (б), 570 (в) | № 529 (в), 570 (г) |
| Решить задачу: | |
| Бронза состоит из 3 частей олова и 17 частей меди. Сколько олова в бронзовой детали, если масса детали 660 г? | Смесь, состоящая из 3 частей грузинского чая и 4 частей индийского чая, имеет массу 210 г. Сколько граммов грузинского чая в этой смеси? |
IV. Итог урока. 1) Дать пояснение к задаче № 615.
2) Отгадать чайнворд (№ 625).
V. Домашнее задание. п. 14, повторить п. 3, 4; № 622, 617, 625 (г).
Урок тема:Порядок выполнения действий
Цели: научить различать действия первой ступени и действия второй ступени, правильно выполнять порядок действий.
Оборудование: плакат для устного счета, магниты; презентация
Ход урока
I. Устные упражнения. Презентация. Упростите выражение: а) 2а + 612 + 7а + 324
б) 38 + 5а + 75 + 6а.
II. Изучение нового материала.
| 1. | Умножение, деление |
| Сложение, вычитание | 2-я ступень |
| 1-я ступень | |
2. Три правила выполнения действий (работа с учебником).
3. Рассмотреть примеры № 1–4.
4. Изменить порядок действий можно на основе свойств сложения, вычитания и умножения.
III. Закрепление.
1. Повторить теоретический материал по вопросам п. 15.
2. Решить у доски:
а) № 627 (а); б) 627 (в); в) 627 (д); г) 627 (и).
а) № 628 (а); б) 628 (г); в) 628 (д); г) 628 (в).
3. Самостоятельная работа обучающего характера.
№ 627 (е, з); 639 (а, д, ж); 642.
IV. Итог урока. Тренировка внимания.
Учитель показывает ребятам плакат и обращается к ним: «Внимательно посмотрите на плакат. Вам дается 1 секунда, после чего плакат будет убран, а вы должны сложить три числа, которые были на нем, и назвать сумму этих чисел».

Эксперимент заключается в том, что дана установка: назвать сумму трех чисел. А вопросы будут иметь другое содержание: какое число записано внутри квадрата, треугольника и круга.
V. Домашнее задание. п. 15 (до программ и команд); № 647 (а, б, ж, з), 648 (б, г), 650.
Урок Тема:Порядок выполнения действий
Цели: закрепить навык в выполнении порядка действий; научить составлять программу и схему программы вычислений.
Оборудование: ксерокопии тестов каждому ученику; таблица для ответов, калька, презентация
Ход урока
I. Проверка домашнего задания.
II. Устные упражнения. презентация
№ 638 (а, в).
III. Изучение нового материала.
1. Изложение теоретического материала согласно учебнику: при разборе примера (можно взять для начала проще, чем в учебнике) соответственно чертится схема вычислений.
(68 – 15) 4 = 212
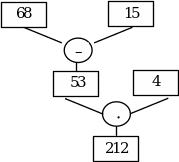
IV. Закрепление.
1. Каким правилам подчиняется порядок выполнения действий?
2. № 628 (б, е), 627 (б, г, и), 629, 631, 632 (а).
3. На повторение самостоятельно: 639 (з, к), 639 (б, м), 640.
V. Итог урока.
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
VI. Домашнее задание: п. 15; № 632, 631, 634 (а, в). Составить числовое выражение из 4 действий и схему к нему.
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
Тест
1) Значение числового выражения равно 100. Где нужно поставить скобки?
а) (140 : 4 + 3) 5; б) 140 : (4 + 3 5); в) 140 : (4 + 3) 5.
2) Дано выражение 157 18 – 57 18. Как нужно изменить порядок действий, чтобы удобно было считать?
а) 157 – 18 57; б) 158 18 – 57; в) 18 (157 – 57).
Урок тема:Порядок выполнения действий (п. 15)
Цели: выработать навык правильного выполнения порядка действий, составления схем для вычисления значений числовых выражений.
Оборудование: карточки к самостоятельной работе.
Ход урока
I. Проверка домашнего задания.
Запишите эту программу в виде схемы. Найдите значение выражения.
II. Устные упражнения.
№ 634 (д), 635, 637, 638 (б, г).
III. Работа по теме урока.
1. Что такое команда? (Последовательность выполнения действий в выражении). № 630 (ниже дан образец выполнения).
Числовое выражение: 381 29 – 7248 : 24.
Программа вычислений:
1) Умножить 381 на 29.
2) Разделить 7248 на 24.
3) От результата выполнения команды 1 отнять результат выполнения команды 2.
Схема выполнения.
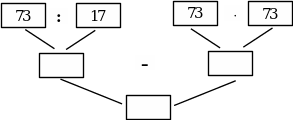
2. № 632 (б).
3. Записать числовые выражения: № 646, 645 (домашние упражнения).
4. Выполнить № 627 (ж, к).
5. Самостоятельная работа по вариантам.
Вариант I: № 627 (л); 643 (1).
Вариант II: № 627 (м); 643 (2).
IV. Итог урока.
1. Ответить на вопросы к п. 15.
2. Соревнование соседей по парте: № 651.
V. Домашнее задание. п. 15 повторить 5, 6; № 644, 647 (в, г, д, е), 649. Составьте числовое выражение из 4 действий и схему к нему.
Урок Тема: Квадрат и куб числа
Цели: научить формулировать определение квадрата и куба числа, возводить числа в квадрат и куб, находить значения числовых выражений, содержащих вторую и третью степень натурального числа.
Оборудование: план изучения темы;презентация.
Ход урока
I. Изучение нового материала, презентация
1. Сообщение темы урока.
2. Изучение соответствует плану (заранее написан на доске).
а) Что называется квадратом числа?
б) Таблица квадратов первых 10 натуральных чисел.
в) Что называется кубом числа?
г) Таблица кубов первых 10 натуральных чисел.
д) В каком порядке выполняются действия, если в числовое выражение входят квадраты и кубы чисел.
II. Закрепление.
1. № 655, 652 (составить таблицу и выучить).
2. № 657 (а, г, и).
3. Самостоятельно: № 657 (б, в).
4. На повторение: № 663. Девочки – № 665 (1), мальчики № 665 (2).
III. Устные упражнения.
1. 23 – 4; 2) 52 + 22; 3) 152 – 25.
2. Каков порядок действий: а) 160 + 37 – 20 + 52.
б) 90 – 60 : 15.
3. «Быстро сообрази».
Найдите математический термин из четырех букв, который служит окончанием слов:
Пери…, диа…, мано…
IV. Домашнее задание. п. 16; № 666, 671, 669, 673. Выучить таблицу квадратов (от 1 до 20) и кубов (от 1 до 7), повторить п. 7, 8.
Поставить скобки так, чтобы равенство было верным:
9664 : 32 – 2 195 – 37 5 = 3000.
Урок тема: Квадрат и куб числа
Цели: выработать навык в вычислении значения выражения, содержащего квадрат и куб числа.
Оборудование: карточки, таблицы, калька для выполнения теста; набор карточек с числами от 1 до 20.
Ход урока
I. Выполнить тест.
| I вариант | II вариант |
| 1) Вычислите: 1) Вычислите: | |
| 82 а) 64; б) 16; в) 2; г) 8. | 103 а) 30; б) 3; в) 10; г) 1000. |
| 2) Вычислите: 1) Вычислите: | |
| 2 43 а) 24; б) 128; в) 512; г) 32. | 3 52 а) 45; б) 30; в) 225; г) 75. |
| 3) Упростите выражение: Упростите выражение | |
| 11а – а – 21 | 11у + у + 3 |
| а) 11а –2; б) 8а; в) 3а; в) 10 а – 2 | а) 11у + 3; б) 12у + 3; в) 14у; г) 15у. |
| 4) Найдите значение выражения: Найдите значение выражения | |
| у3 – 2 при у = 6. а) 16; б) 216; в) 214; д) 64. | х2 + 5 при х = 11 а) 126; б) 121; в) 27; г) 256. |
| 5) Упростите выражение: Упростите выражение: | |
| 19 –(14 + с) а) 5с; б) 5 + с; в) 33 – с; г) 5 – с. | 15 – (b + 2) а) 17 – b; б) 13 – b; в) 13b; г) 13 + b. |
| 6) Для того чтобы разность 2874 945 12 была верной, вместо надо поставить цифру: а) 9; б) 1; в) 0; г) 3. | 6) Для того чтобы разность 3284 648 22 была верной, вместо надо поставить цифру: а) 3; б) 7; в) 6; г) 4. |
II. Тренировочные упражнения:
1. № 657 (д, з, е, ж), 658.
2. На повторение: № 664, 665 (з, и).
а) Вычислите (43 – 72) 84.
III. Домашнее задание. п. 14–16; № 668,670, 672. Таблицы квадратов и кубов. Прочитать с. 117. Подготовиться к контрольной работе.
Урок Тема: Контрольная работа №5 по теме «Упрощение выражений»
| I вариант | II вариант |
| 1) Найдите значение выражения: 1) Найдите значение выражения | |
| а) (1142600 – 890778) : 74 + + 309 708. б) 132 + (52 – 49)3 | а) 508 609 – (223136 + 18916) : 69 б) (44 – 38)2 + 132 |
| 2) Решите уравнение: 2) Решите уравнение: | |
| а) 4а + 8а = 204 б) 12у – 7у = 315 | а) 5m + 6m = 231 б) 7х – 3х = 412 |
| 3) Решите задачу: 3) Решите задачу: | |
| В двух пачках 168 тетрадей. В одной пачке в 3 раза меньше тетрадей, чем в другой. Сколько тетрадей в меньшей пачке? | В двух ящиках 75 кг яблок. В первом ящике в 2 раза больше яблок, чем во втором. Сколько яблок во втором ящике? |
| 4) Упростите выражение 4) Упростите выражение | |
| 147 + 23х + 39х и найдите его значение при х = 3 и при х = 10 | 67х + 133 + 27х и найдите его значение при х = 4 и при х = 10 |
| 5) У Коли несколько трехкопеечных и несколько пятикопеечных монет. Всего 80 копеек. Трехкопеечных монет у него столько же, сколько и пятикопеечных. Сколько трехкопеечных монет у Коли? | 5) У Сережи столько двухкопеечных монет, сколько и гривенников. Все монеты составляют сумму 60 копеек. Сколько двухкопеечных монет у Сережи? |
II. Домашнее задание.
а) Решить другой вариант.
б) Познакомиться с п. 17.
| I вариант | II вариант |
| 1) Найдите значение выражения: 1) Найдите значение выражения | |
| а) (1142600 – 890778) : 74 + + 309 708. б) 132 + (52 – 49)3 | а) 508 609 – (223136 + 18916) : 69 б) (44 – 38)2 + 132 |
| 2) Решите уравнение: 2) Решите уравнение: | |
| а) 4а + 8а = 204 б) 12у – 7у = 315 | а) 5m + 6m = 231 б) 7х – 3х = 412 |
| 3) Решите задачу: 3) Решите задачу: | |
| В двух пачках 168 тетрадей. В одной пачке в 3 раза меньше тетрадей, чем в другой. Сколько тетрадей в меньшей пачке? | В двух ящиках 75 кг яблок. В первом ящике в 2 раза больше яблок, чем во втором. Сколько яблок во втором ящике? |
| 4) Упростите выражение 4) Упростите выражение | |
| 147 + 23х + 39х и найдите его значение при х = 3 и при х = 10 | 67х + 133 + 27х и найдите его значение при х = 4 и при х = 10 |
| 5) У Коли несколько трехкопеечных и несколько пятикопеечных монет. Всего 80 копеек. Трехкопеечных монет у него столько же, сколько и пятикопеечных. Сколько трехкопеечных монет у Коли? | 5) У Сережи столько двухкопеечных монет, сколько и гривенников. Все монеты составляют сумму 60 копеек. Сколько двухкопеечных монет у Сережи? |
| I вариант | II вариант |
| 1) Найдите значение выражения: 1) Найдите значение выражения | |
| а) (1142600 – 890778) : 74 + + 309 708. б) 132 + (52 – 49)3 | а) 508 609 – (223136 + 18916) : 69 б) (44 – 38)2 + 132 |
| 2) Решите уравнение: 2) Решите уравнение: | |
| а) 4а + 8а = 204 б) 12у – 7у = 315 | а) 5m + 6m = 231 б) 7х – 3х = 412 |
| 3) Решите задачу: 3) Решите задачу: | |
| В двух пачках 168 тетрадей. В одной пачке в 3 раза меньше тетрадей, чем в другой. Сколько тетрадей в меньшей пачке? | В двух ящиках 75 кг яблок. В первом ящике в 2 раза больше яблок, чем во втором. Сколько яблок во втором ящике? |
| 4) Упростите выражение 4) Упростите выражение | |
| 147 + 23х + 39х и найдите его значение при х = 3 и при х = 10 | 67х + 133 + 27х и найдите его значение при х = 4 и при х = 10 |
| 5) У Коли несколько трехкопеечных и несколько пятикопеечных монет. Всего 80 копеек. Трехкопеечных монет у него столько же, сколько и пятикопеечных. Сколько трехкопеечных монет у Коли? | 5) У Сережи столько двухкопеечных монет, сколько и гривенников. Все монеты составляют сумму 60 копеек. Сколько двухкопеечных монет у Сережи? |
Урок Тема: Формулы
Цели: научить определять, что такое формула, закрепить формулу пути (времени, скорости); учить вычислять по формуле.
Оборудование: карточки с индивидуальными заданиями по работе над ошибками; карточки с числом для № 668; раздаточный материал: прямоугольник и квадрат.
Ход урока
I. Анализ контрольной работы.
а) Общий анализ контрольной работы.
б) Объяснение заданий, с которыми не справились большинство учеников.
в) Демонстрация лучших работ.
Карточки с индивидуальными заданиями можно вложить в тетради с контрольной работой.
II. Устные упражнения.
1. № 686. (Учитель показывает карточку с числом, ученики находят квадраты чисел; аналогично находятся кубы чисел).
2. № 684 (а, б). (Выясняется, является ли полученный результат квадратом какого-либо числа?)
3. № 690, 692 – полуписьменно.
III. Изучение нового материала.
1. Работа по учебнику.
Запись в тетради: S – путь; – скорость; t – время.
Формула пути: ![]()
2. По учебнику разбирается задача № 2. t = S : .
3. Задача № 3 = S : t.
4. Вспоминаются известные формулы.
Если а и b – стороны треугольника, Р – периметр, то Р = (а + b) 2.
5. Если а – стороны квадрата, то Р = 4а.
6. Если а – делимое, b – делитель, q – неполное частное и r – остаток, то а = b q + r.
IV. Закрепление.
1. Что называется формулой?
2. Какое равенство называется формулой пути?
3. Что из этой формулы можно найти?
4. Какие еще формулы знаете?
5. На повторение: № 698 (устно), № 693 (а, в).
V. Итог урока. Практическая работа.
1) Измерить стороны прямоугольника и вычислить периметр.
2) Измерить сторону квадрата и вычислить периметр.
3) Сравнить полученные периметры.
VI. Домашнее задание. п. 17 (знать все изученные формулы и уметь их применять); № 701, 704, 707 (а, б); 708 (а).
Урок тема: Формулы
Цели: научить читать и записывать формулы, производить вычисления по формулам.
Оборудование: Презентация
Ход урока
I. Проверка домашнего задания.
Устно проверить решение № 704.
II. Устные упражнения.
1. Вычислить: Презентация.
2. № 687, 691, 688 (а, б, в).
III. Тренировочные упражнения.
1. На доске прикреплена ромашка, на лепестках которой с обратной стороны записаны задания из № 675 (б), 676 (б), 679 (а), 679 (б), 678 (б), 677 (б), 683 и такое задание:
Выразите m из формулы а = 150 : m + 1 (всего 8 лепестков).
(4 человека вызываются к доске, после ответа одного вызываются по одному; можно включить дополнительный вопрос).
2. На повторение № 693 (б, г).
3. Самостоятельная работа на оценку:
Вариант I – № 699 (1); вычислить: (23 + 52) 3.
Вариант II – № 699 (2); вычислить: (62 + 33) : 21
IV. Итог урока.
1. Повторить все формулы.
2. Какие формулы нужно использовать при решении домашнего задания № 702, 703.
V. Домашнее задание. п. 17, повторить п. 7, 8; № 702, 703, 707 (в, г), 708 (б).
Урок Тема: Площадь. Площадь прямоугольника
Цели: сформировать понятия квадратного сантиметра, площади фигуры; научить находить площадь прямоугольника, сложной фигуры, научить определять равные фигуры.
Оборудование: квадрат со стороной 1 см; раздаточный материал (по две фигуры, разбитые на кв. сантиметры); демонстрационные равные фигуры.
Ход урока
I. Проверка домашнего задания.
Консультанты до урока проверили домашние работы у учащихся и докладывают о их выполнении.
II. Устные упражнения.
1. Восстановить цепочку вычислений.
![]()
2. (70 : 5 +2) 4 – 64 Результат разделить на 11.
(48 : 4 – 2) 9 : 45 + 18 Результат возвести в квадрат.
3. Можно ли указать число, которое не является корнем уравнения:
а) х : х = 1; б) 0 : х = 0; в) m : 0 = 0; г) 1 = ?
4. Наименьшее четырехзначное число уменьшите на 100. Какой получится результат?
III. Изучение нового материала.
1) Что такое квадратный сантиметр?
2) Как найти площадь фигуры?
3) Рассмотреть примеры рис. 62, 63; найти площади фигур, лежащих на парте у учащихся.

4) S – площадь прямоугольника, а – длина, b – ширина.
S = аb.
5) Определение равных фигур (продемонстрировать).
6) Каковы площади равных фигур?
7) Чему равна площадь всей фигуры, если фигура разделена на части?
IV. Закрепление.
1. Устно № 709, 711, 712, 714.
2. № 716, 717.
3. На повторение: № 731, 732.
V. Итог урока.
Ответить на вопросы или найти в учебнике ответ на вопросы к п. 18.
VI. Домашнее задание. п. 18 (до площади квадрата); № 736, 741 (а), 744, 745.
Урок Тема: Квадрат. Формула площади квадрата
Цели: научить находить площадь треугольника, квадрата.
Оборудование: карточки для проверки домашнего задания; фигуры прямоугольника, квадрата, опорный конспект. Презентация
Ход урока
I. Проверка домашнего задания.
1. Проверить фронтально только ответы.
2. Устный счет: Презентация.
Вариант I
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 32 см | 7 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 3 см2.
Вариант II
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 27 см | 8 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 4 см2.
II. Устные упражнения.
1. Найти значение выражения: 52 + 32; (27 – 17)3; 13 + 23; 52 22; 03 + 42.
2. № 724 (б), 723 (в, г, д), 726 (а, в).
III. Изучение нового материала.
1. Повторить по вопросам п. 18 (ч. 1).
2. На экран проецируется рис. 64 (работа с учебником).
3. Нахождение площади треугольника.
4. Определение квадрата.
5. Формула площади квадрата S = а2.
6. Повторение единиц площади.
IV. Закрепление.
1. Устно № 710, 715, 719, 720.
2. № 713, 718.
3. На повторение: № 734 (по вариантам).
V. Итог урока.
VI. Домашнее задание. п. 18; 738, 739, 742 (б), 741 (а, б).
Вариант I
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 32 см | 7 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 3 см2.
Вариант II
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 27 см | 8 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 4 см2.
Вариант I
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 32 см | 7 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 3 см2.
Вариант II
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 27 см | 8 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 4 см2.
Вариант I
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 32 см | 7 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 3 см2.
Вариант II
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 27 см | 8 см |
|
|
Вариант I
1) Заполните таблицу, где а и b – стороны прямоугольника.
| а | b | S | Р |
| 32 см | 7 см |
|
|
2) Начертите две неравные фигуры, имеющие одинаковую площадь 3 см2.
Урок Тема: Единицы измерения площади
Цели: научить учащихся отвечать на вопрос, какие единицы измерения площадей существуют, переводить одни единицы измерения площадей в другие, использовать знания при решении задач.
Оборудование: таблица единиц площади; индивидуальные задания для практической работы, презентация
Ход урока
I. Практическая работа.
Ученикам раздаются листы с чертежами прямоугольника и квадрата. Выполнить необходимые измерения и вычислить площадь и периметр фигур.
II. Устные упражнения. Презентация
№ 764 (а), 763 (а, б), 767.
III. Изучение нового материала.
1. Вспомнить, какие единицы измерения площади ученики знают.
2. Что такое квадратный миллиметр, квадратный сантиметр?
3. Что такое гектар?
4. Что за единица измерения площади 1 ар?
5. Что надо помнить при вычислении площадей?
6. Повторение единиц площади.
IV. Закрепление.
1. Вывешивается таблица, ученики изучают ее слева направо и наоборот.
2. № 748, 749, 751, 756 (а, б).
3. На повторение: № 583, 589.
V. Итог урока.
Ответить на вопросы п. 19.
VI. Домашнее задание. п. 19; 779, 781 (б), 784, 789 (а).
Урок Тема:Единицы измерения площади
Цели: научить учащихся отвечать на вопрос, какие единицы измерения площадей существуют, переводить одни единицы измерения площадей в другие, использовать знания при решении задач.
Оборудование: карточки для проверки домашнего задания.
Ход урока
I. Проверка домашнего задания.
1. За первые парты: 6 человек.
2. У доски: 4 человека.
3. Остальные выполняют устные упражнения.
За первыми партами:
Вариант I
1) Одна сторона прямоугольника равна 3 м, а другая на 2 м больше. Найдите площадь.
2) Найдите площадь треугольника ACD, если АВ = 3 см, AD = 6 см.

Отвечающие у доски:
1. Как найти площадь всей фигуры, если известна площадь всех частей этой фигуры?
2. 1) Найдите периметр прямоугольника, площадь которого равна 30 см2, а одна из его сторон – 5 см.
2) Что можно сказать о площадях равных фигур?
3. 1) Длина прямоугольника 32 см, а его ширина в 4 раза меньше. Чему равна площадь прямоугольника?
2) Что такое гектар?
4. 1) Найдите площадь всей фигуры, если даны следующие размеры: AD = АВ = 4 см, DN = 6 см.
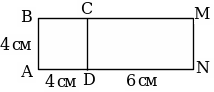
2) Назовите в порядке возрастания единицы измерения площади.
II. Устные упражнения.
№ 554 (б), 765 (а, б, в), 772.
III. Тренировочные упражнения по теме урока.
1. № 747 (в, а), 750, 753, 756 (в), 760.
2. На повторение: № 769, 774, 776 (1, 2).
IV. Итог урока.
Вопросы к п. 19, таблица единиц площади.
V. Домашнее задание. п. 19; № 778, 780 (а), 785, 789 (б).
Урок Тема: Единицы измерения площади
Цели: научить учащихся отвечать на вопрос, какие единицы измерения площадей существуют, переводить одни единицы измерения площадей в другие, использовать знания при решении задач.
Оборудование: ксерокопии тестов.
Ход урока
I. Самостоятельная работа.
| I вариант | II вариант |
| 1. Найти площадь квадрата, сторона которого равна 11 см. 1) 44 см2; 2) 121 см2; 3) 22 см2; 4) 121 см. | 1. Найти площадь квадрата, сторона которого равна 9 см. 1) 18 см2; 2) 81 см2; 3) 81 см; 4) 36 см2. |
| 2. Найти площадь прямоугольника со сторонами 6 см и 4 см. 1) 24 см2; 2) 10 см2; 3) 20 см2; 4) 24 см. | 2. Найти площадь прямоугольника со сторонами 3 см и 10 см. 1) 26 см2; 2) 30 см2; 3) 13 см2; 4) 30 см. |
| 3. Найти периметр прямоугольника, одна из сторон которого равна 9 см, а его площадь – 36 см2. 1) 4 см; 2) 324 см; 3) 13 см; 26 см. | 3. Найти периметр прямоугольника, площадь которого равна 40 см2, а одна из его сторон равна 5 см. 1) 26 см; 2) 8 см; 3) 13 см; 4) 200 см. |
| 4. Найти площадь фигуры. 1) 14 см2; 2) 35 см2; 3) 26 см2; 4) 27 см2. | 4. Найти площадь фигуры. 1) 48 см2; 2) 24 см2; 3) 33 см2; 4) 39 см2. |
| 5. Найти площадь четырех-угольника ABCD. 1) 7 см2; 2) 14 см2; 3) 4 см2; 4) 9 см2. | 5. Найти площадь четырёхугольника ABCD. 1) 7 см2; 2) 14 см2; 3) 4 см2; 4) 9 см2. |
II. Устные упражнения.
№ 763 (в, г, д), 733, 768.
III. Тренировочные упражнения.
№ 752 (с комментированием с места); № 756 (г), 755, 759.
IV. Итог урока.
V. Домашнее задание. п. 19 повторить; № 770, 773, 777.
Урок тема: Прямоугольный параллелепипед
Цели: сформировать понятие прямоугольного параллелепипеда, куба, научить находить ребра и грани, вычислять площадь поверхности прямоугольного параллелепипеда.
Оборудование: модели параллелепипеда, куба; плакат с числовым кроссвордом; индивидуальные листы с чертежом для итога урока. Презентация.
Ход урока
I. Устные упражнения. Презентация
II. Изучение нового материала. Презентация
П. 20 – объяснение учителя с использованием моделей в соответствии с учебником.
III. Закрепление.
1. Ответ на вопросы п. 20.
2. № 791, 790, 792 (а), 953.
3. На повторение: № 805, 808 (самостоятельно)
IV. Итог урока.
Каждому выдается лист с заданием:
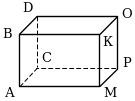
1) Рассмотрите рисунок и впишите пропущенные слова.
На рисунке изображен прямоугольный_____________________.
Точка К – его _________________________________________.
Отрезок АВ – его ______________________________________.
Прямоугольник АВКМ – его _____________________________.
2) Обведите равные ребра параллелепипеда одним цветом.
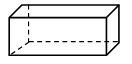
V. Домашнее задание. п. 20; № 811, 814, 816, 817 (а), 818.
Из плотной бумаги сделать прямоугольный параллелепипед, измерения которого равны:
Вариант I: а = 15 см, b = 12 см, с = 8 см.
Вариант II: а = 18 см, b = 10 см, с = 6 см.
Урок Тема:Объемы. Объем прямоугольного
параллелепипеда.
Цели: сформировать понятия «больший объем», «меньший объем», «равенство объемов», научить вычислять объем прямоугольного параллелепипеда и куба.
Оборудование: два неравных сосуда, подкрашенная жидкость для сравнения объемов; два равных сосуда; модели кубического сантиметра, кубического дециметра; Презентация
Ход урока
I. Устные упражнения.
№ 830 (а), 829 (а, б), 831 (а, б).
II. Изучение нового материала. Презентация
План изложения нового материала.
1) Сравнение объемов.
2) Единицы измерения объемов.
3) Что такое 1 см3, 1 дм3?
4) Вывод правила вычисления объема прямоугольного параллелепипеда.
5) Формула объема прямоугольного параллелепипеда.
6) Как можно прочитать формулу V = abc.
7) Формула объема куба: V = а3.
III. Закрепление.
1. Ответить на вопросы п. 21 (вопросы 1–4).
2. Устно: № 814, 820 (а, в), 826, 823 – самостоятельно.
3. На повторение: № 814 (1, 2) – самостоятельно.
IV. Итог урока.
1. Предложить ученикам ответить на вопросы «Что нового узнали на уроке? Чему научились?».
2. А теперь я научу вас, как строить прямоугольный параллелепипед. Строим следующим образом:
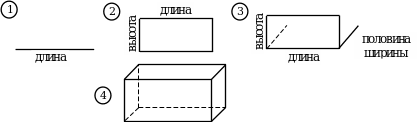
V. Домашнее задание. п. 21; № 839, 841, 846 (а), 848 (а, в).
Практическая работа: сделать необходимые измерения и вычислить объем своей комнаты.
Урок Тема:Объемы. Соотношения между
единицами объема.
Цели: научить переводить одни единицы объема в другие; закрепить навык вычисления объемов прямоугольного параллелепипеда и куба.
Оборудование: тесты, таблица ответов.
Ход урока
I. Проверка домашнего задания.
Выполнить тестирование по вариантам.
I вариант
1. В прямоугольном параллелепипеде ABCDMKSP равны ребра (см. рис.):
1) АМ и PS; 2) РМ и DC; 3) PD и ВК; 4) AB и KS.
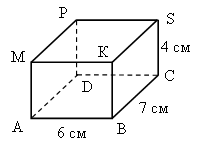
2. В прямоугольном параллелепипеде ABCDMKSP равны грани (см. рис.):
1) MPDA и MPSK; 2) MABK и DPSC;
3) MABK и KBCS; 4) DPSC и MPDA.
3. Найдите объем прямоугольного параллелепипеда, длина которого 6 см, ширина – 2 см, а высота – 3см.
1) 12 см3; 2) 11 см3; 3) 36 см3; 4) 15 см3.
4. Найдите объем куба с ребром, равным 4 м.
1) 16 м3; 2) 12 м3; 3) 4 м3; 4) 64 м3.
II. Устные упражнения.
1. № 829 (в, г, д), 835, 832.
2. Решите анаграммы: ДВАКАТР, РОЗТЕКО, ТЕРГАК.
Объясните, что означает каждое слово.
Ответ: квадрат, отрезок, гектар.
III. Изучение нового материала.
План беседы.
1) Вспомнить, что такое 1 см3, 1 дм3.
2) Провести аналогию: 1 мм3, 1 м3, 1 км3.
3) 1 м3 = 103 дм3 = 1000 дм3 = 1000 л.
4) 1 л = 1 дм3 = 1000 см3 1 см3 = 1000 мм3
5) 1 км3 = 1 000 000 000 м3.
IV. Закрепление.
1. Назвать единицы измерения объема, начиная с самой малой.
2. Решить: № 825 (а, б, в), 820 (б, д), 824, 821, 828.
3. На повторение № 837 (самостоятельно).
V. Итог урока.
1. Повторить формулы объема.
2. Вопросы п. 21 (№ 5–8).
3. № 849.
VI. Домашнее задание. п. 21; № 840, 844, 846 (е, г), 848 (б, д), 834. Познакомиться с № 838.
I вариант
1. В прямоугольном параллелепипеде ABCDMKSP равны ребра (см. рис.):
1) АМ и PS; 2) РМ и DC; 3) PD и ВК; 4) AB и KS.

2. В прямоугольном параллелепипеде ABCDMKSP равны грани (см. рис.):
1) MPDA и MPSK; 2) MABK и DPSC;
3) MABK и KBCS; 4) DPSC и MPDA.
3. Найдите объем прямоугольного параллелепипеда, длина которого 6 см, ширина – 2 см, а высота – 3см.
1) 12 см3; 2) 11 см3; 3) 36 см3; 4) 15 см3.
4. Найдите объем куба с ребром, равным 4 м.
1) 16 м3; 2) 12 м3; 3) 4 м3; 4) 64 м3.
| Фамилия, имя класс | ||||
| Номер задания | 1 | 2 | 3 | 4 |
| Номер ответа |
|
|
|
|
Вариант II
1. В прямоугольном параллелепипеде ABCDMKSP равны ребра (см. рис.):
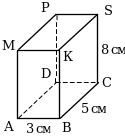
1) AD и PS; 2) МК и DC;
3) PD и ВС; 4) ВС и МК.
2. В прямоугольном параллелепипеде ABCDMKSP равны грани (см. рис.):
1) АМКВ и KBCS;
2) ADCB и BKSC;
3) MPDA и AMKB;
4) MPDA и KSCB.
3. Найдите объем прямоугольного параллелепипеда, длина которого равна 4 см, ширина – 2 см, а высота – 3 см.
1) 24 см3; 2) 8 см3; 3) 12 см3; 4) 9 см3.
4. Найдите объем куба с ребром, равным 5 дм.
1) 25 дм3; 2) 125 дм3; 3) 15 дм3; 4) 5 дм3.
| Фамилия, имя класс | ||||
| Номер задания | 1 | 2 | 3 | 4 |
| Номер ответа |
|
|
|
|
Урок Тема: Объемы. Соотношения между
единицами объема
Цели: научить переводить одни единицы объема в другие; закрепить навык вычисления объемов прямоугольного параллелепипеда и куба.
Оборудование: на отдельном плакате каждая изученная формула; магнитная доска, набор магнитов.
Ход урока
I. Проверка домашнего задания.
II. Устные упражнения.
1. Вспомнить все изученные формулы: S = t; = S : t; t = S : ; Р = (а + b) 2; Р = 4а; а = bq + r; S = ab; S = a2; V = abc; V = a3.
2. Вычислить устно: 23 + 32; 33 + 52; 43 + 6; 103 – 10.
3. № 834.
III. Работа по теме урока.
1. № 820 (г), 825 (а, б, в) – с комментариями с места, № 822, 827.
2. Самостоятельная работа обучающего характера (ДМ, В. 2, 3).
| Вариант I | Вариант II | |
| 1) Найти объем прямоугольного параллелепипеда, измерения которого равны: | Найти объем прямоугольного параллелепипеда, измерения которого равны: | |
| 24 м, 30 м и 450 дм. | 26 дм, 25 дм и 4 м. | |
| 2) Объем физкультурного зала 1800 м3. Его высота 5 м. Какова площадь пола? | 2) Объем ящика 13600 см3. Найдите площадь дна этого ящика, если его высота 16 см. | |
| 3) Чему равен объем куба, ребро которого 11 см? | 3) Чему равен объем куба, ребро которого 12 см? | |
| Дополнительное задание: Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 2 раза, но больше высоты на 4 см. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем. | Дополнительное задание: Длина прямоугольного параллелепипеда 24 см, и она больше ширины в 3 раза, а ширина на 3 см меньше высоты. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем. | |
IV. Итог урока.
Заполнить таблицы.
| Скорость, v | Время, t | Расстояние, S |
| Длина: а | 3 дм | 16 см |
| 5 см |
| 18 км/ч | 3 ч |
|
| Ширина: b | 4 дм |
| 20 дм |
|
| 90 км/ч |
| 450 км |
| Площадь: S |
| 64 см2 | 80 дм2 |
|
|
| 20 ч | 600 км |
| Периметр: P |
|
|
| 24 |
V. Домашнее задание. п. 21, повторить п. 17–19; № 845, 843, 846 (в), 848 (г, е). Подготовиться к контрольной работе.
| Вариант I | Вариант II | |
| 1) Найти объем прямоугольного параллелепипеда, измерения которого равны: | Найти объем прямоугольного параллелепипеда, измерения которого равны: | |
| 24 м, 30 м и 450 дм. | 26 дм, 25 дм и 4 м. | |
| 2) Объем физкультурного зала 1800 м3. Его высота 5 м. Какова площадь пола? | 2) Объем ящика 13600 см3. Найдите площадь дна этого ящика, если его высота 16 см. | |
| 3) Чему равен объем куба, ребро которого 11 см? | 3) Чему равен объем куба, ребро которого 12 см? | |
| Дополнительное задание: Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 2 раза, но больше высоты на 4 см. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем. | Дополнительное задание: Длина прямоугольного параллелепипеда 24 см, и она больше ширины в 3 раза, а ширина на 3 см меньше высоты. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем. | |
| Вариант I | Вариант II | |
| 1) Найти объем прямоугольного параллелепипеда, измерения которого равны: | Найти объем прямоугольного параллелепипеда, измерения которого равны: | |
| 24 м, 30 м и 450 дм. | 26 дм, 25 дм и 4 м. | |
| 2) Объем физкультурного зала 1800 м3. Его высота 5 м. Какова площадь пола? | 2) Объем ящика 13600 см3. Найдите площадь дна этого ящика, если его высота 16 см. | |
| 3) Чему равен объем куба, ребро которого 11 см? | 3) Чему равен объем куба, ребро которого 12 см? | |
| Дополнительное задание: Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 2 раза, но больше высоты на 4 см. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем. | Дополнительное задание: Длина прямоугольного параллелепипеда 24 см, и она больше ширины в 3 раза, а ширина на 3 см меньше высоты. Найдите: а) сумму длин всех ребер; б) площадь его поверхности; в) объем. | |
Урок Тема: Контрольная работа № 6 по теме «Площади и объемы»
Вариант I
1. Найдите по формуле S = t:
а) путь S, если t = 3 ч, = 408 км/ч.
б) время t, если S = 7200 м, = 800 м/мин.
2. Длина прямоугольного участка земли 650 м, а ширина на 50 м меньше. Найдите площадь участка и выразите ее в гектарах.
3. Длина прямоугольного параллелепипеда 45 см, ширина в 3 раза меньше длины, а высота на 2 см больше ширины. Найдите объем параллелепипеда.
4. Найдите значение выражения:
17040 – 69 238 – 43776 : 72.
5. Длина прямоугольника 84 см. Насколько уменьшится площадь прямоугольника, если его ширину уменьшить на 5 см?
Вариант II
1. Найдите по формуле S = t:
а) путь S, если t = 11 ч, = 65 км/ч.
б) скорость , если S = 600 км, t = 50 с.
2. Ширина прямоугольного участка земли 600 м, а длина на 150 м больше. Найдите площадь участка и выразите ее в гектарах.
3. Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 3 раза. Высота параллелепипеда на 12 см меньше длины. Найдите объем параллелепипеда.
4. Найдите значение выражения:
350 92 – 66600 : 36 + 9670.
5. Ширина прямоугольника 44 см. Насколько уменьшится площадь этого прямоугольника, если его длину уменьшить на 5 см?
Домашнее задание.
Решить другой вариант. На урок принести циркуль, линейку.
Вариант I
1. Найдите по формуле S = t:
а) путь S, если t = 3 ч, = 408 км/ч.
б) время t, если S = 7200 м, = 800 м/мин.
2. Длина прямоугольного участка земли 650 м, а ширина на 50 м меньше. Найдите площадь участка и выразите ее в гектарах.
3. Длина прямоугольного параллелепипеда 45 см, ширина в 3 раза меньше длины, а высота на 2 см больше ширины. Найдите объем параллелепипеда.
4. Найдите значение выражения:
17040 – 69 238 – 43776 : 72.
5. Длина прямоугольника 84 см. Насколько уменьшится площадь прямоугольника, если его ширину уменьшить на 5 см?
Вариант II
1. Найдите по формуле S = t:
а) путь S, если t = 11 ч, = 65 км/ч.
б) скорость , если S = 600 км, t = 50 с.
2. Ширина прямоугольного участка земли 600 м, а длина на 150 м больше. Найдите площадь участка и выразите ее в гектарах.
3. Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 3 раза. Высота параллелепипеда на 12 см меньше длины. Найдите объем параллелепипеда.
4. Найдите значение выражения:
350 92 – 66600 : 36 + 9670.
5. Ширина прямоугольника 44 см. Насколько уменьшится площадь этого прямоугольника, если его длину уменьшить на 5 см?
Вариант I
1. Найдите по формуле S = t:
а) путь S, если t = 3 ч, = 408 км/ч.
б) время t, если S = 7200 м, = 800 м/мин.
2. Длина прямоугольного участка земли 650 м, а ширина на 50 м меньше. Найдите площадь участка и выразите ее в гектарах.
3. Длина прямоугольного параллелепипеда 45 см, ширина в 3 раза меньше длины, а высота на 2 см больше ширины. Найдите объем параллелепипеда.
4. Найдите значение выражения:
17040 – 69 238 – 43776 : 72.
5. Длина прямоугольника 84 см. Насколько уменьшится площадь прямоугольника, если его ширину уменьшить на 5 см?
Вариант II
1. Найдите по формуле S = t:
а) путь S, если t = 11 ч, = 65 км/ч.
б) скорость , если S = 600 км, t = 50 с.
2. Ширина прямоугольного участка земли 600 м, а длина на 150 м больше. Найдите площадь участка и выразите ее в гектарах.
3. Ширина прямоугольного параллелепипеда 14 см, она меньше длины в 3 раза. Высота параллелепипеда на 12 см меньше длины. Найдите объем параллелепипеда.
4. Найдите значение выражения:
350 92 – 66600 : 36 + 9670.
5. Ширина прямоугольника 44 см. Насколько уменьшится площадь этого прямоугольника, если его длину уменьшить на 5 см?
Урок Тема:Окружность и круг
Цели: научить учащихся понимать, что такое окружность, круг, давать определения и строить радиус, диаметр, полукруг, полуокружность.
Оборудование: циркуль, линейка. Презентация
Ход урока
I. Анализ контрольной работы.
а) Общий анализ контрольной работы.
б) Объяснение заданий, с которыми не справились многие ученики.
в) Демонстрация лучших работ.
Карточки с индивидуальными заданиями для работы над ошибками ученики получают вместе с тетрадью для контрольных работ.
II. Устные упражнения.
1. Заполните клетки:
![]()
Является ли полученное число квадратом какого-либо числа?

Получившееся число возвести в куб и отнять 64.
2. № 861, 863.
III. Изучение нового материала. Презентация
Изложение учебного материала можно провести по плану:
1) Понятие окружности, определение круга, центра.
2) Свойства точек окружности.
3) Определение радиуса и диаметра.
4) Соотношение длин радиуса и диаметра.
5) Понятие полукруга, полуокружности, дуги, концов дуги.
IV. Закрепление.
1. Устно № 850.
2. Практическая работа № 851, 859, 855.
3. На повторение: № 868 (найти опечатку в учебнике: не сторона куба, а длина ребра куба).
№ 870, самостоятельно № 872 (1).
V. Итог урока.
Найти в тексте ответы на вопросы п. 22.
VI. Домашнее задание. п. 22 (то, что отмечено чертой); № 874, 875, 878 (а, в, д), 883 (а, в).
Урок Тема:Окружность, круг. Круговые шкалы
Цели: закрепить понятия окружности, круга, полукруга, полуокружности, дуги, навык построения этих фигур.
Оборудование: циркуль, линейка; модели шкал, расположенных по окружности и на дугах окружности; билеты с вопросами для проверки домашнего задания; Презентация, набор магнитов, магнитная доска.
Ход урока
I. Проверка домашнего задания.
Устные упражнения. Презентация
1. № 860 (в, г, д).
Содержание билетов.
Билет № 1
а) Рассказать, как строят окружность с помощью циркуля. Какой отрезок называется радиусом окружности? Построить окружность и радиус.
б) Перечислить свойства сложения.
Билет № 2
а) Какой отрезок называется диаметром окружности? Начертить его. Во сколько раз диаметр длиннее радиуса?
б) Как называются числа при сложении? Как найти неизвестное слагаемое (привести пример).
Билет № 3
а) Есть ли у окружности два радиуса различной длины? А два диаметра различной величины?
б) Как из числа отнять сумму двух чисел? Привести пример.
Билет № 4
а) Что называется кругом? Что такое окружность?
б) Как из суммы вычесть число? Привести примеры.
II. Изучение нового материала.
1. Сообщение темы урока.
2. Учащиеся читают соответствующий пункт учебника, а затем беседуют по содержанию пункта.
III. Закрепление.
1. Устно № 857, 858.
2. Письменно № 852, 854.
3. На повторение № 867, 871 (1) самостоятельно.
IV. Итог урока.
Узнайте, как называется наука, занимающаяся изучением 2. Верно ли высказывание: «Слово «цирк» и «циркуль» имеют одинаковое этимологическое происхождение». Для проверки дома воспользуйтесь этимологическим словарем.
V. Домашнее задание. п. 22, повторить п. 8, 9; № 876, 878, 880 (б, г, е), 883 (б, г).