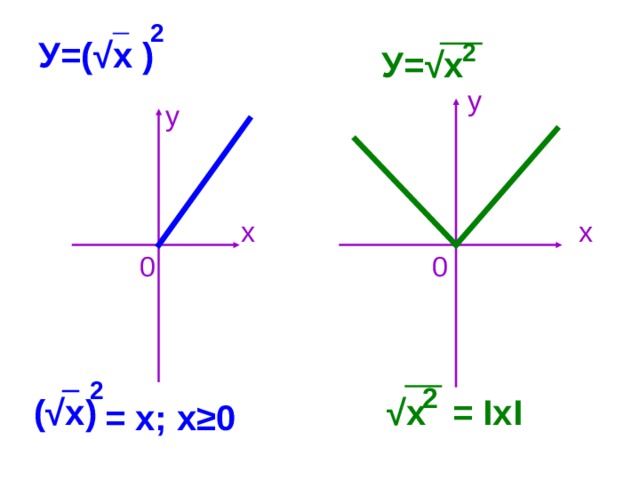Повторяем функции ОГЭ математика

Урок повторения 9 кл

Тема урока: «Функции и их графики».

Цель урока: повторение и систематизация знаний и формирование практических навыков.

Задачи урока:

Образовательные:

правильно употреблять функциональную терминологию;

уметь распознавать графики функций;

иметь наглядное представление о некоторых свойствах функций;

закрепить навыки построения простейших графиков функций,

использование их при решении уравнений.

Развивающие:

расширение кругозора;

быстрота реакции;

развитие математической речи при комментировании решений.

Воспитательные:

воспитание взаимопомощи в процессе выполнения работы в парах;

воспитание внимания, собранности и аккуратности;

формирование адекватной самооценки.

Оборудование:

1. Мультимедийная установка.

2. Карточки с индивидуальными заданиями.

(Вступительное слово учителя)

Идея функциональной зависимости восходит к древности, она содержится уже в первых формулах для нахождения объемов и площадей фигур (4-5 тысяч лет назад).

Начиная с 17 века понятие «функция» становится одним из важнейших. Функция сыграла и поныне играет большую роль в познании реального мира.

Функция – это математическая модель, позволяющая изучать и описывать разнообразные зависимости между реальными величинами.

Умение анализировать эти зависимости сделает вас в дальнейшем успешными в своем поле деятельности.

В настоящее время построение графиков функций, использование свойств функций при решении уравнений необходимо для успешной сдачи экзаменов.

Сегодня на уроке мы повторим все ранее изученные функции, их графики и некоторые свойства.

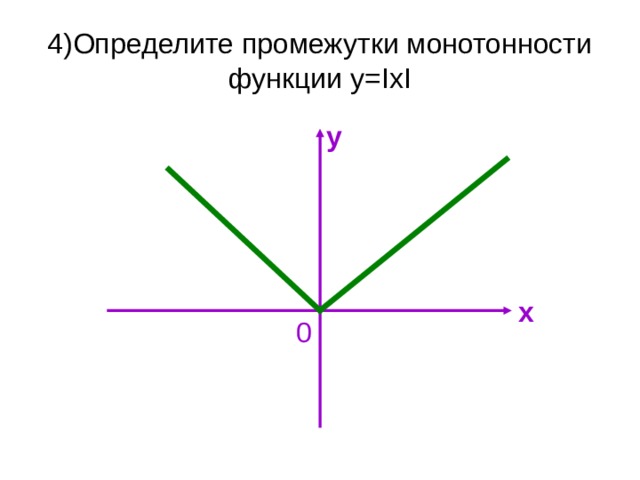
I. Устная работа (задания проектируются на экран):

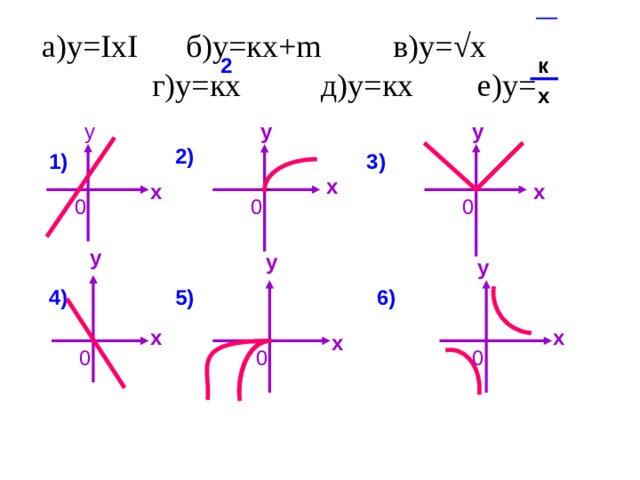
1) Установите соответствие между графиками функций и формулами, задающими эти функции: (ученик должен сказать название функции и графика)

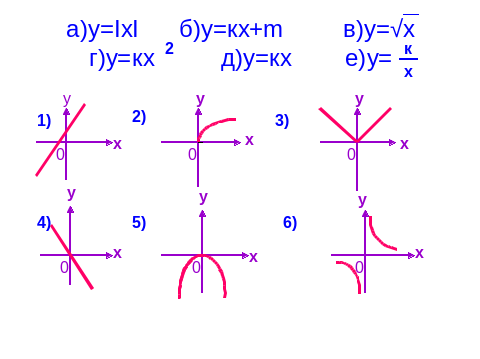
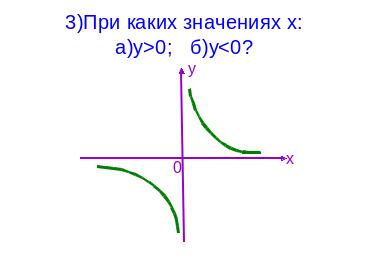
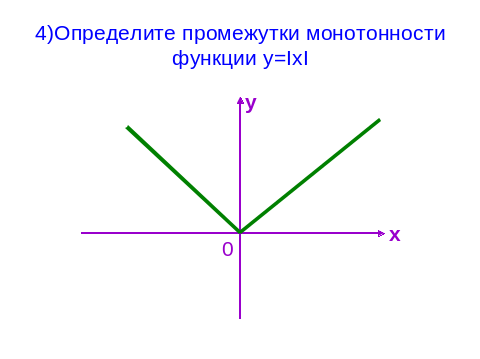
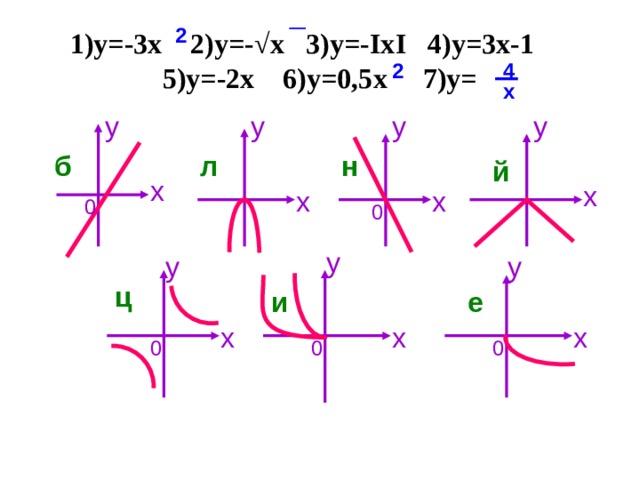
II. (Задание выполняет весь класс. Нужно выписать буквы, соответствующие верным ответам. Получится слово «Лейбниц». Учитель контролирует выполнение задания, при необходимости оказывает помощь.)

Установите соответствие между графиками функций и формулами.

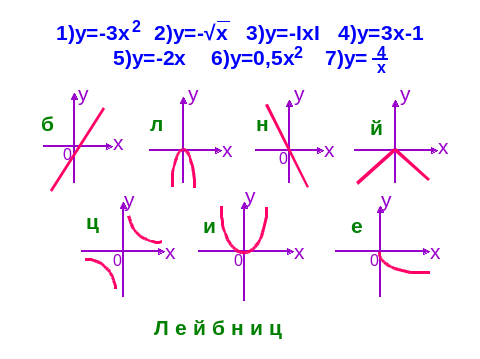
III. (Сообщение учителя. На экран проектируется портрет Вильгельма Лейбница.)

Вильгельм Лейбниц – выдающийся немецкий математик, физик, философ, языковед в 1673 году ввел слово «функция», от латинского function – совершение, выполнение.

IV. (Работа в парах. Учащиеся, по желанию, решение выполняют на листочках, чтобы сдать на проверку. Правильность выполнения задания проверяется с помощью проектора.)

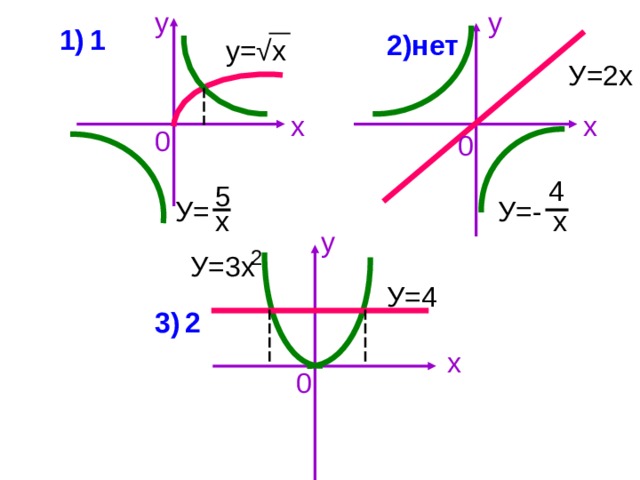
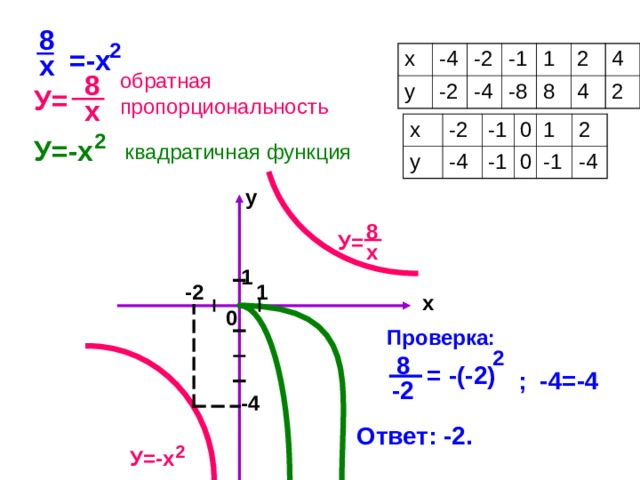
Изобразив схематически графики функций, выясните, имеет ли корни уравнение, и сколько?

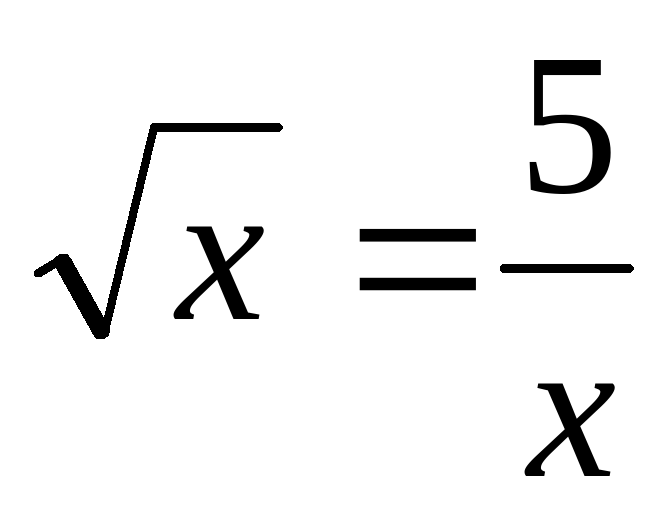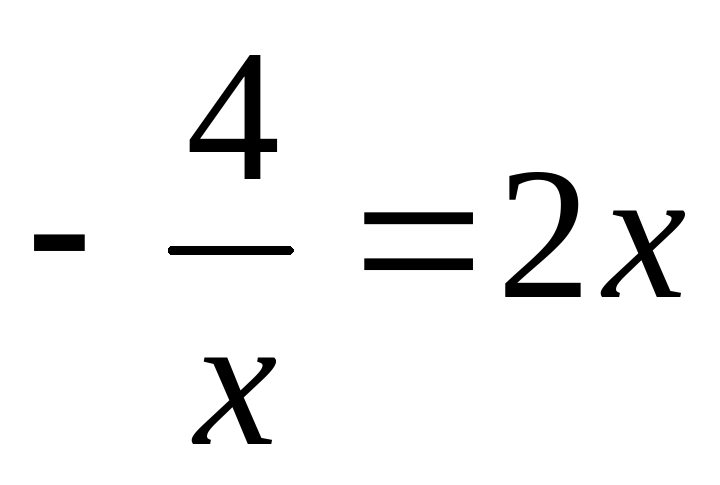1) 2) 3)

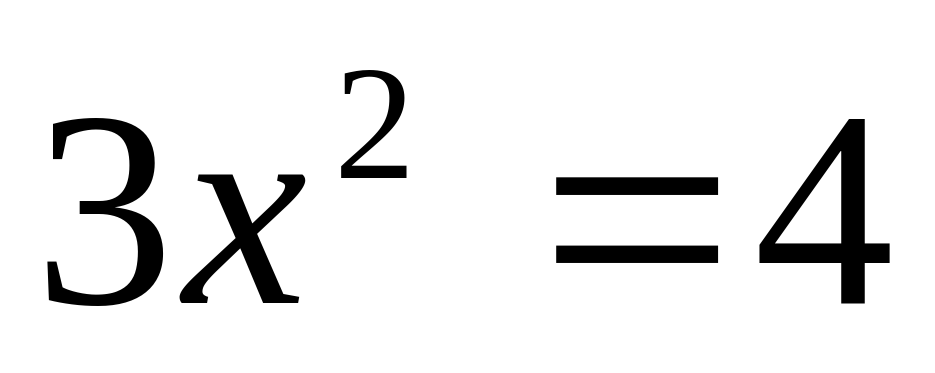
V. (Задание учащиеся выполняют по вариантам. Два ученика решают уравнения с обратной стороны доски. Правильность выполнения и оформления проверяется с помощью проектора. Учитель контролирует выполнение задания, при необходимости помогает учащимся.)

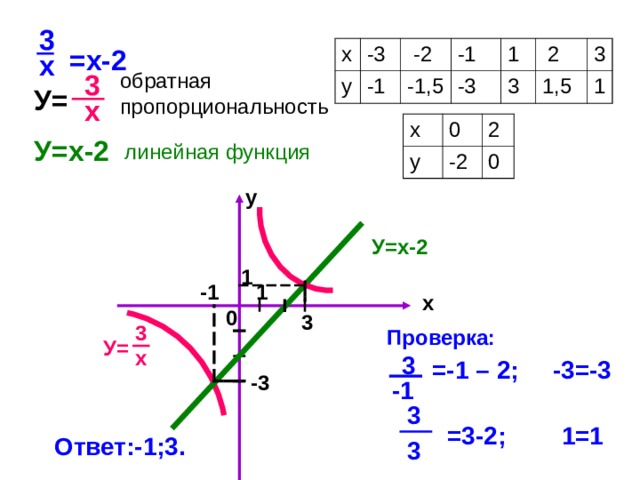
Решите графически уравнение:

I вариант II вариант

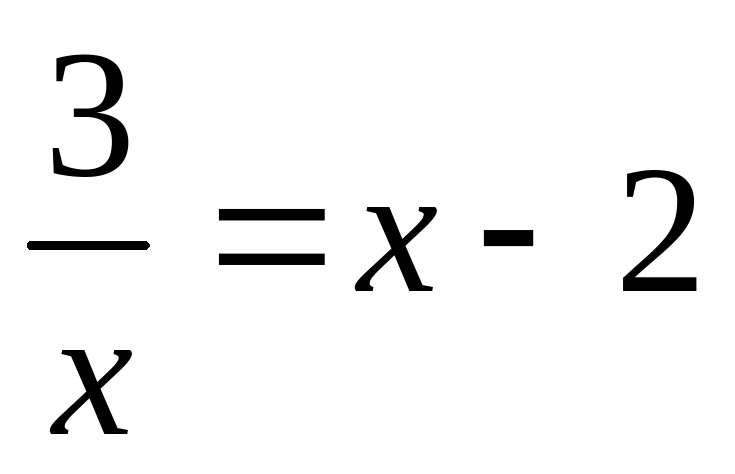
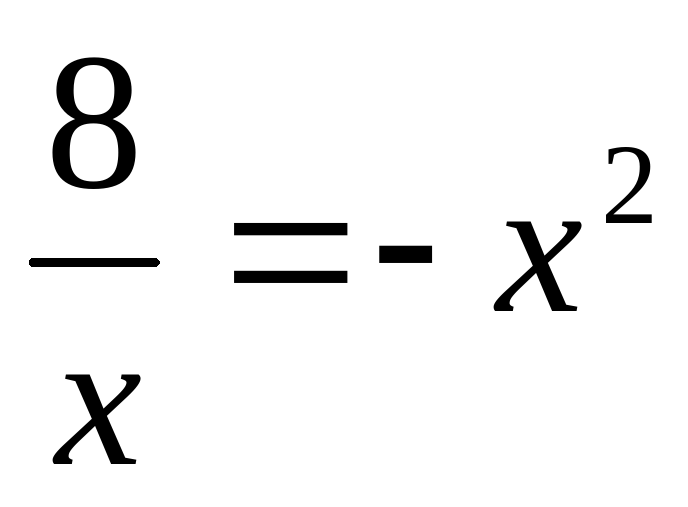
VI. Минута отдыха.

(Задание выполняется устно.)

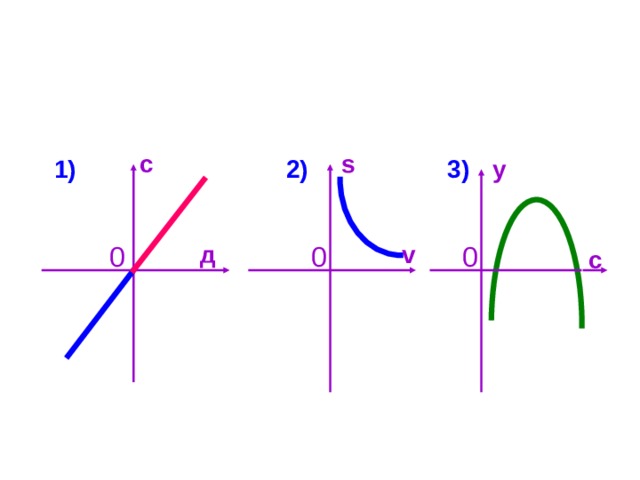
Установите соответствие между пословицами и графиками функций:

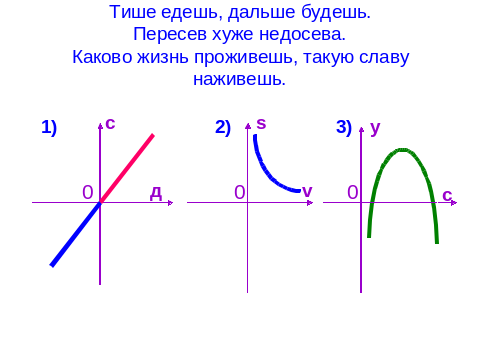
Учитель комментирует все ответы. ( 1)По оси абсцисс – дела, по оси ординат – слава: если дела и поступки положительные, то и слава о человеке идет добрая.

3) По оси абсцисс – семена, по оси ординат – урожай. Для получения высокого урожая необходимо посеять оптимальное количество семян.)

VII. (Тест учащиеся выполняют по вариантам. Учащиеся, по желанию, сдают ответы на листочках. Учитель контролирует выполнение задания. Проверка осуществляется после выполнения задания большинством. Задания, где больше всего встречалось ошибок, разбираются вместе с классом.)

II вариант

Выберите верный ответ:

1)На рисунке изображен график функции вида у=kx+m.

Определите знаки k и m.

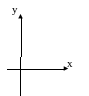
А) k0; m0 Б) kmm0

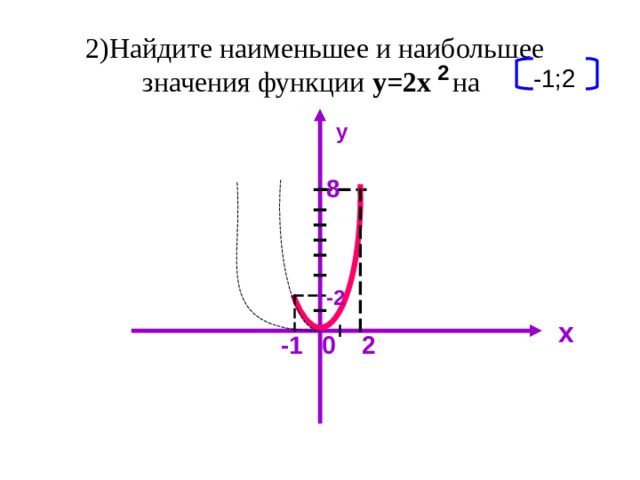
2)Укажите график функции убывающей на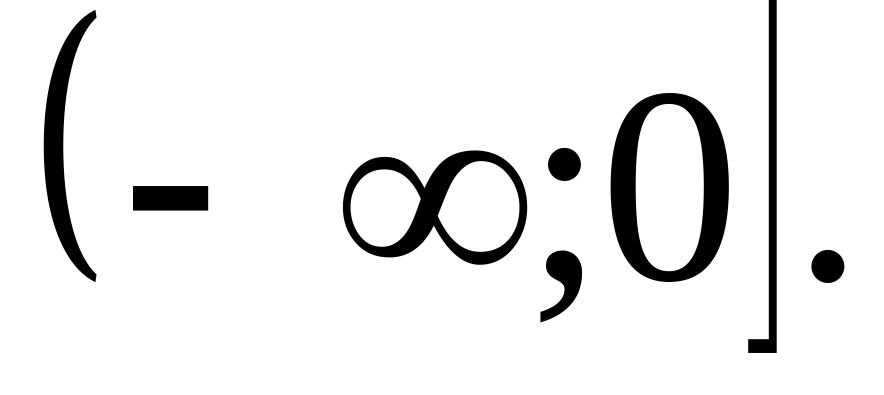

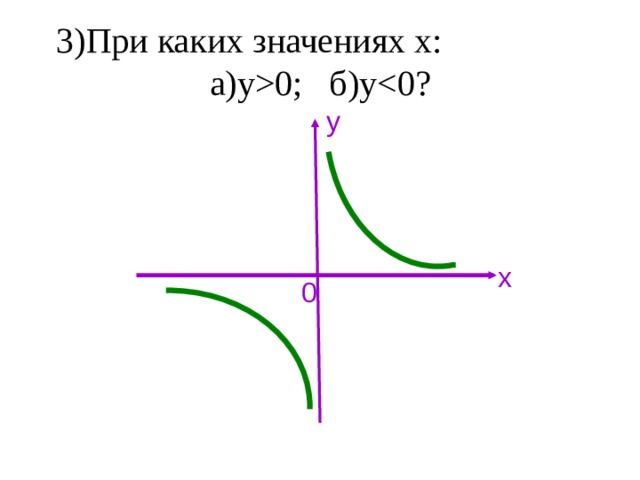
3)Укажите график функции ограниченной снизу.

4)Дан график функции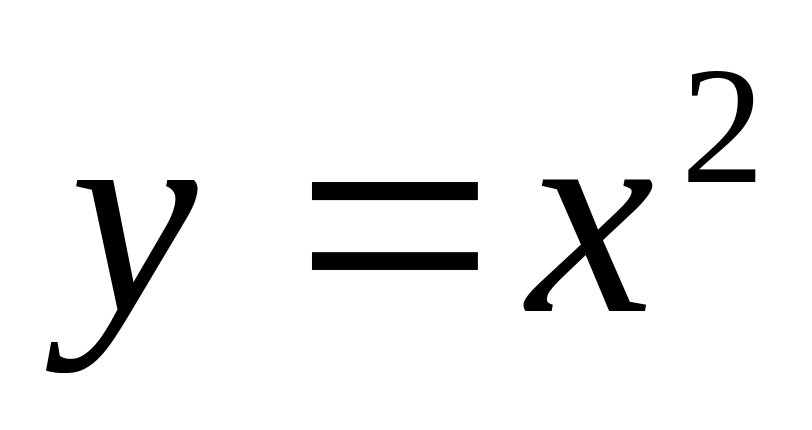 . Какие из утверждений верны?

1.Функция ограничена сверху.

2.

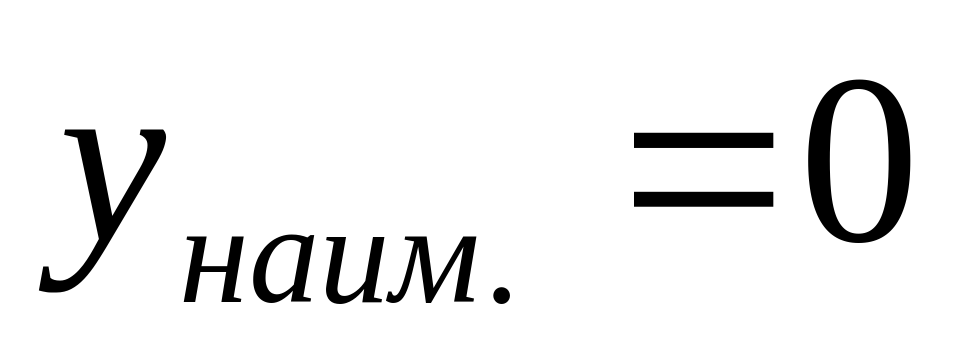
3.Выпукла вверх.

4.Непрерывна.

А) 2 и 4 Б) 1 и 2 В) 2 и 3

I вариант

Выберите букву, соответствующую верному ответу:

1) На рисунке изображен график функции вида у=kх+m.

Определите знаки к и m.

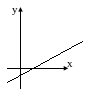
А) k0; m0 Б) k0; mm0

2)Укажите график функции возрастающей на .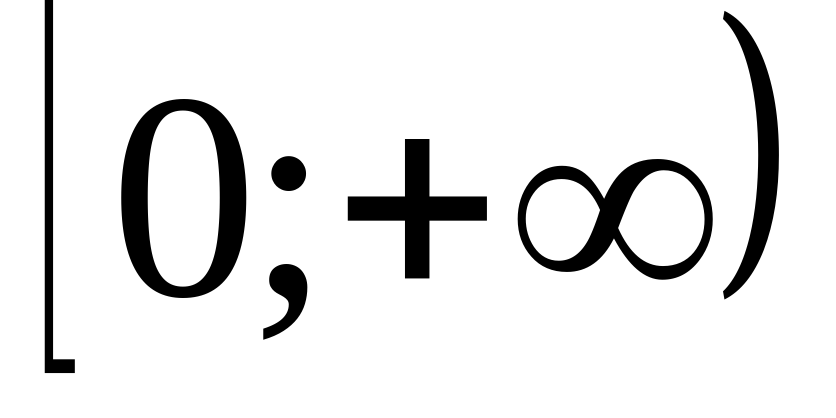

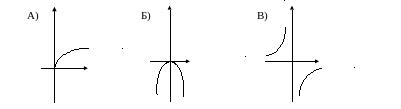
3)Укажите график функции ограниченной сверху.

4)Дан график функции у=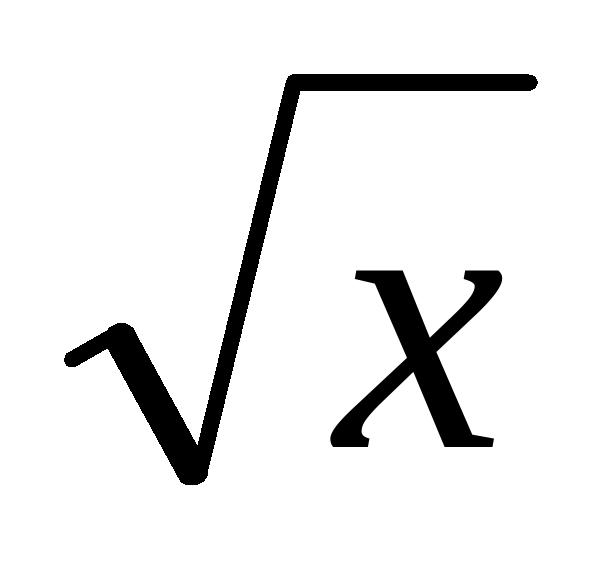 .Какие из утверждений верны:

1.Функция ограничена снизу.

2.

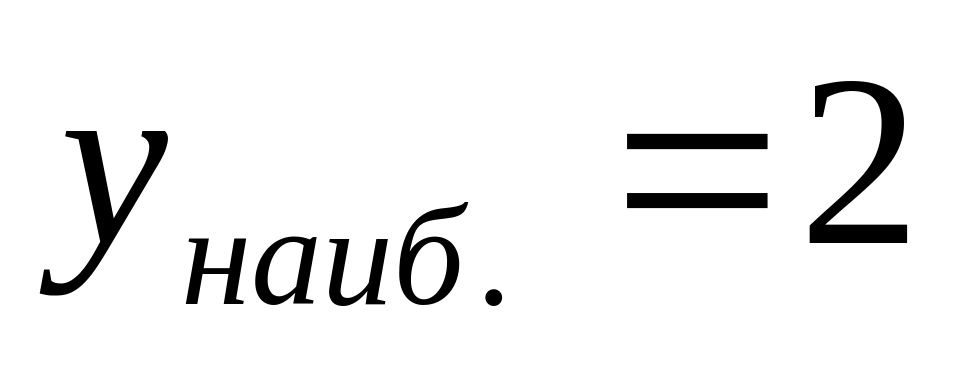
3.Функция непрерывна.

4.Выпукла вниз.

А) 1 и 2 Б) 2 и 3 В) 1 и 3

Ответы

I вариант II вариант

Б А Б В Б Б В А

VIII. (Задание повышенной сложности. Выполняет весь класс. Ученик решает у доски с подробными комментариями.)

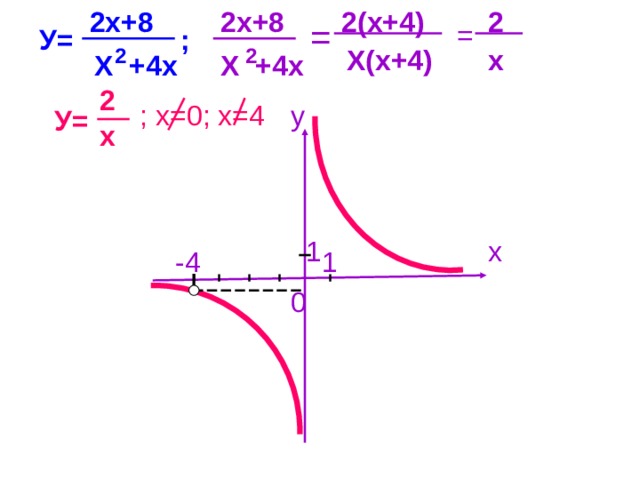
Постройте график функции: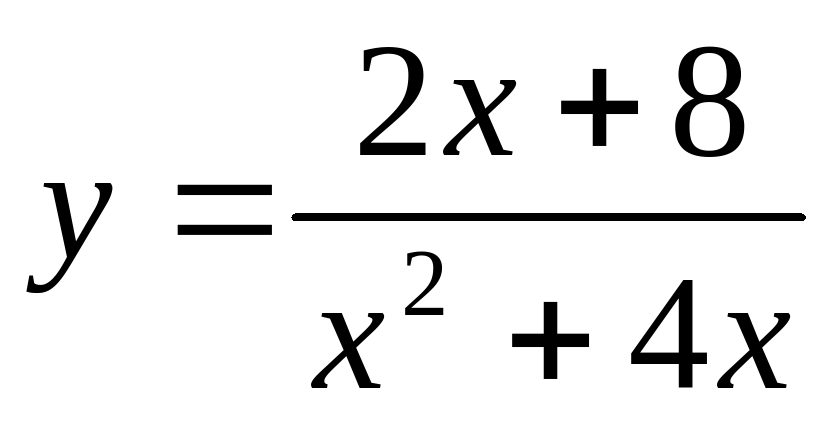

IX. Дополнительное задание. ( Для тех, кто быстро справился с основными заданиями. Проверяем с помощью пректора.)

Постройте графики функций:

а)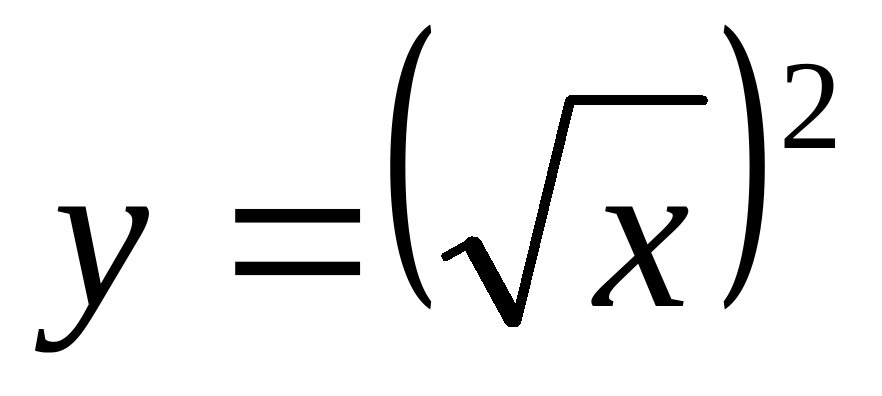 ; б)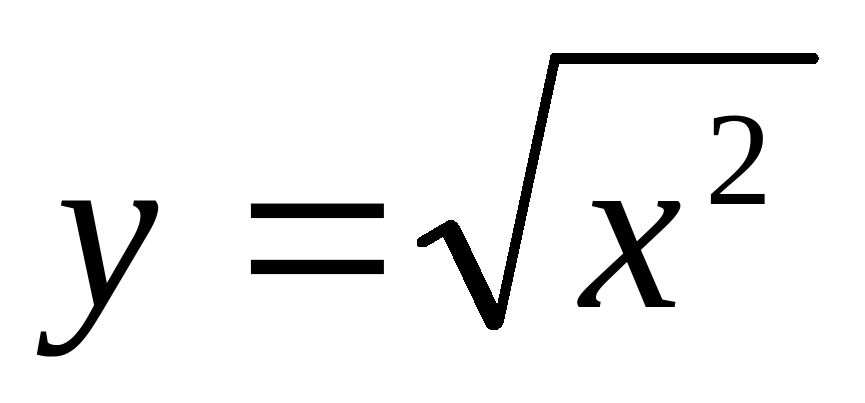

ХI.Домашнее задание.

Составьте уравнения, имеющие три, два, одно решение и не имеющее решения. Подтвердите ваши предположения, схематически изобразив графики.

XII. Итог урока подводит учитель.

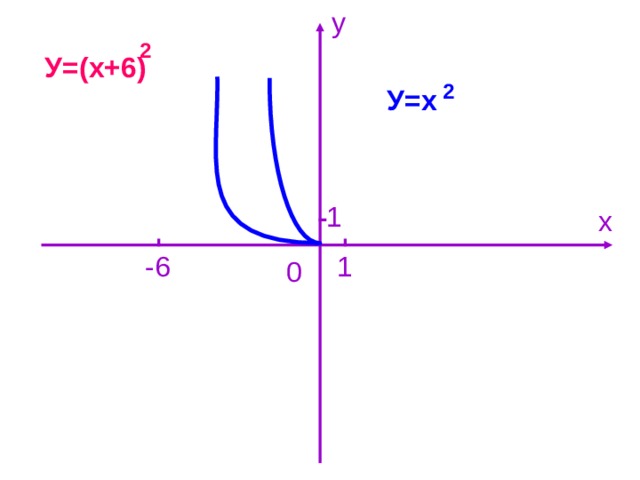
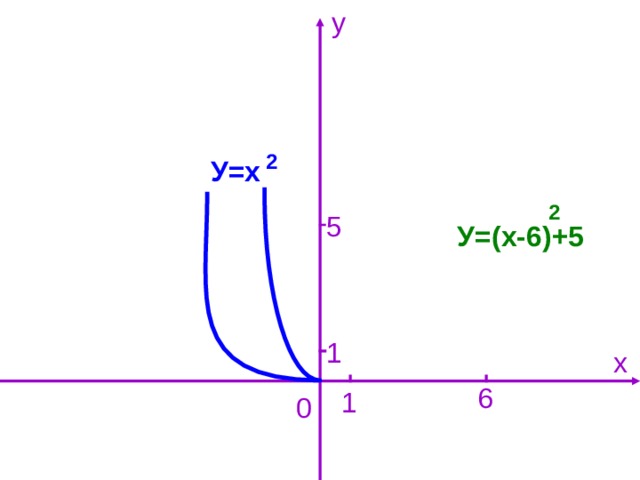
Сегодня на уроке мы повторили все ранее изученные функции, их графики и некоторые свойства. На следующих уроках будем изучать более сложные функции, графики которых получаются из данных путем сдвига вдоль оси х и оси у.

(На экране пример квадратичной функции, которая получается из графика функции у=х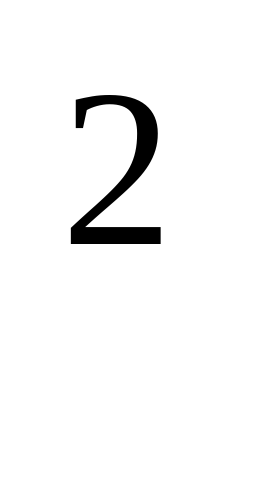 с помощью : а) параллельного переноса вдоль оси х; б) параллельного переноса вдоль оси х и оси у.)

Подведение итогов урока, заполнение учащимися листа самооценки.

Степень сложности урока Степень освоенности материала

Степень интереса познания

Самостоятельная работа

I вариант

I. Cхематически изобразив графики функций, выясните, имеет ли уравнение корни, и сколько?

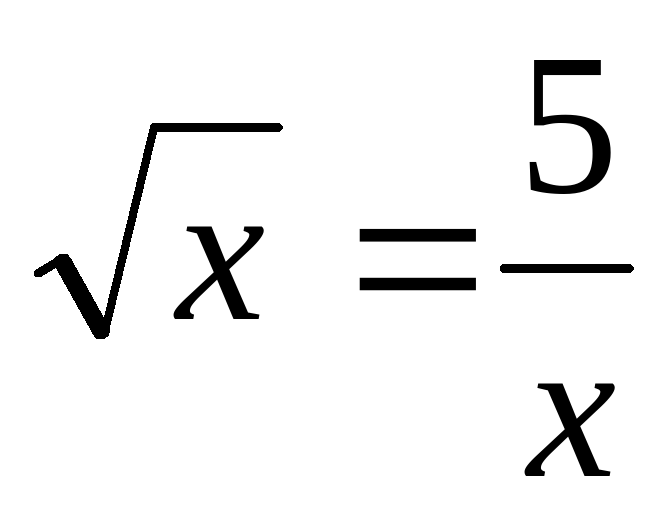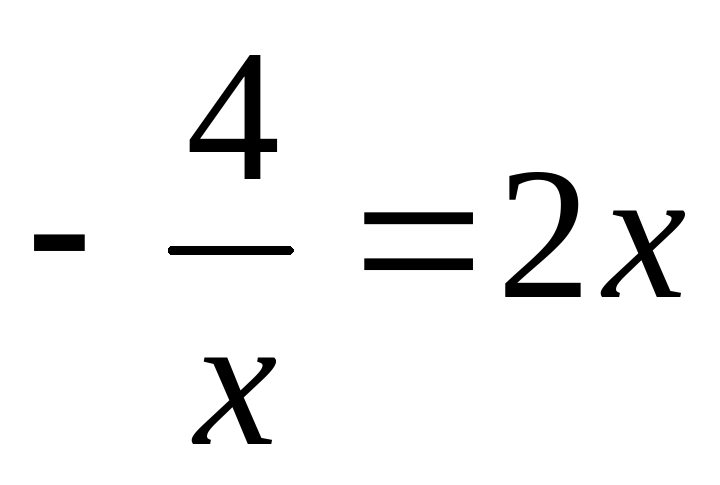1) 2) 3)

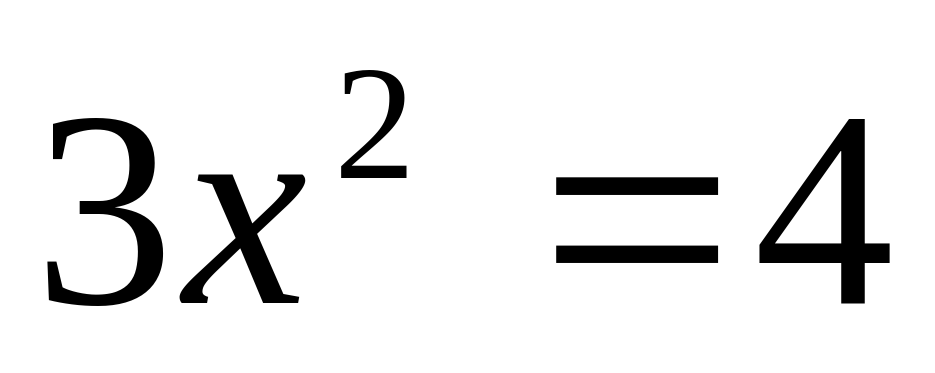
II. Решите графически уравнение:

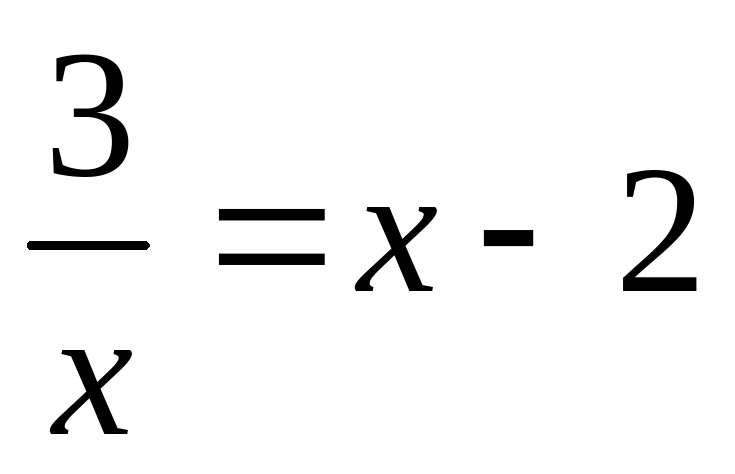
III. Выберите букву, соответствующую верному ответу:

1) На рисунке изображен график функции вида у=kх+m.

Определите знаки к и m.

А) k0; m0 Б) k0; mm0

2)Укажите график функции возрастающей на .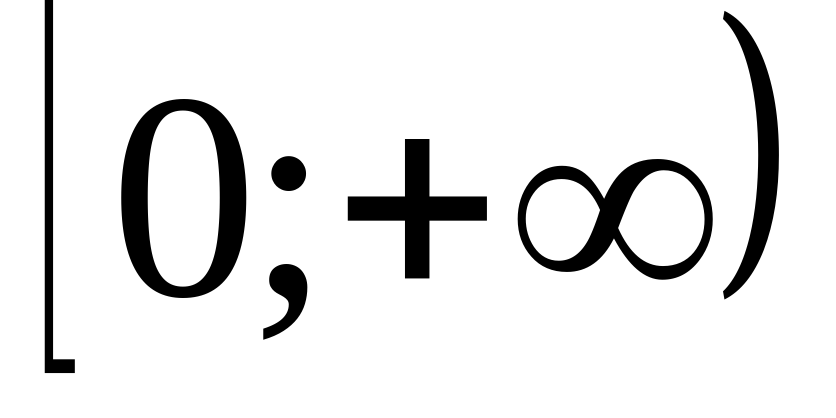

3)Укажите график функции ограниченной сверху.

4)Дан график функции у=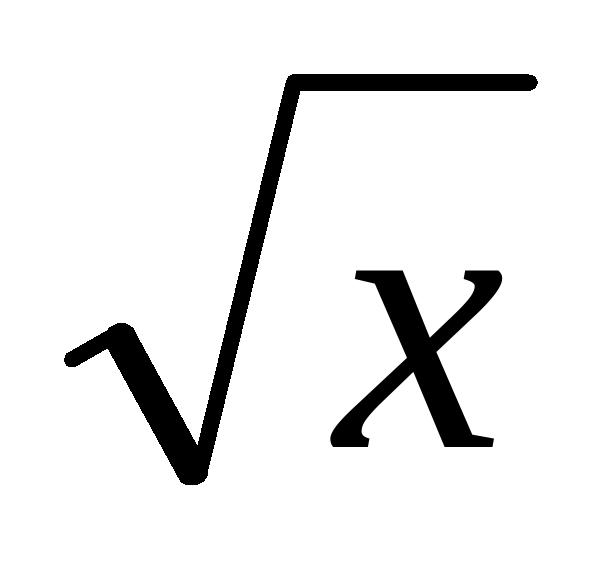 .Какие из утверждений верны:

1.Функция ограничена снизу.

2.

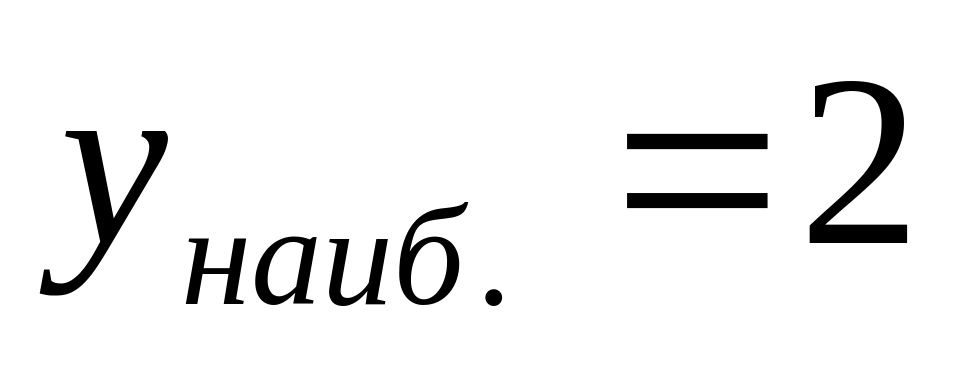
3.Функция непрерывна.

4.Выпукла вниз.

А) 1 и 2 Б) 2 и 3 В) 1 и 3

IV. Постройте график функции: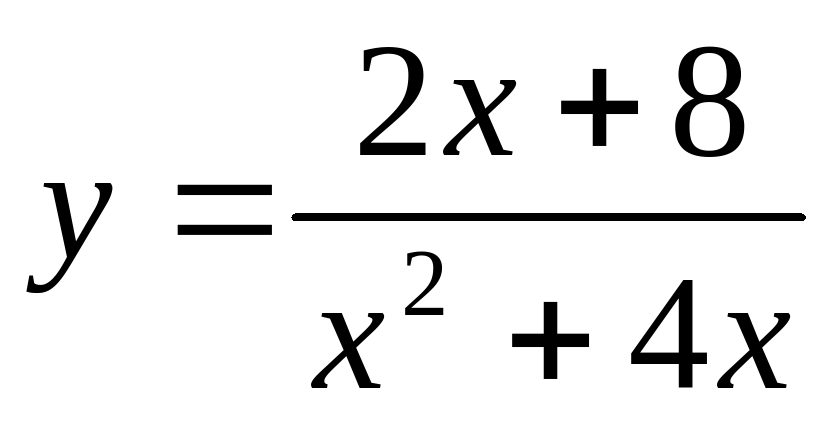

Дополнительные задания:

V.Дана функция у=f(х), где f(х)=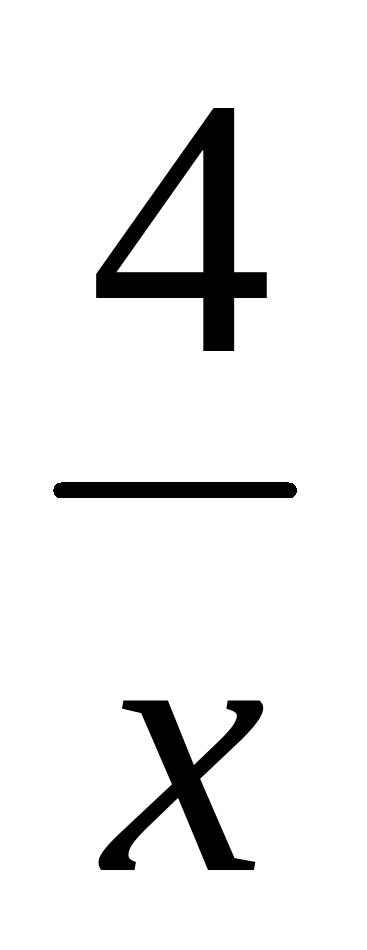 . Решите уравнение

f(x-1)-f(x+1)=1.

VI.Постройте графики функций:

а) ;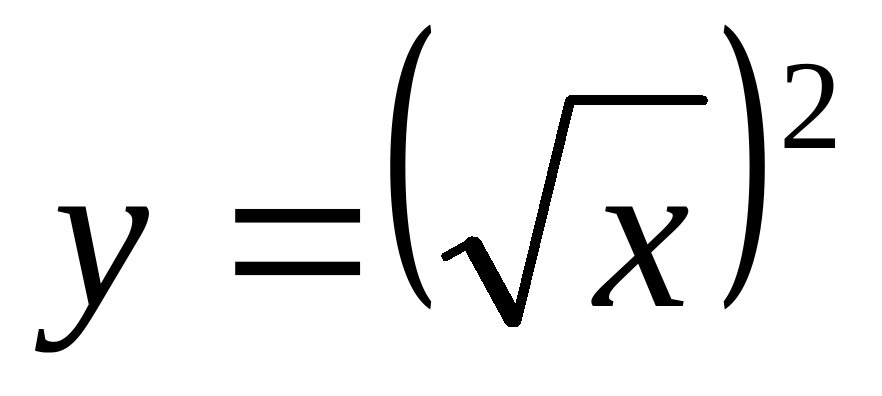

б)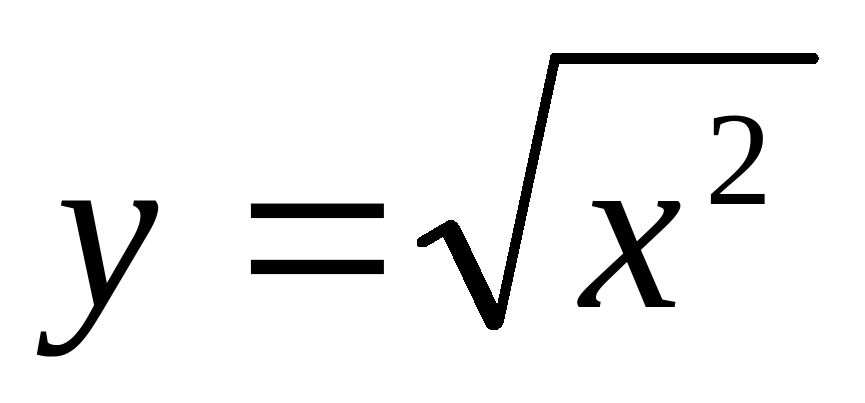

II вариант

I. Cхематически изобразив графики функций, выясните, имеет ли уравнение корни, и сколько?

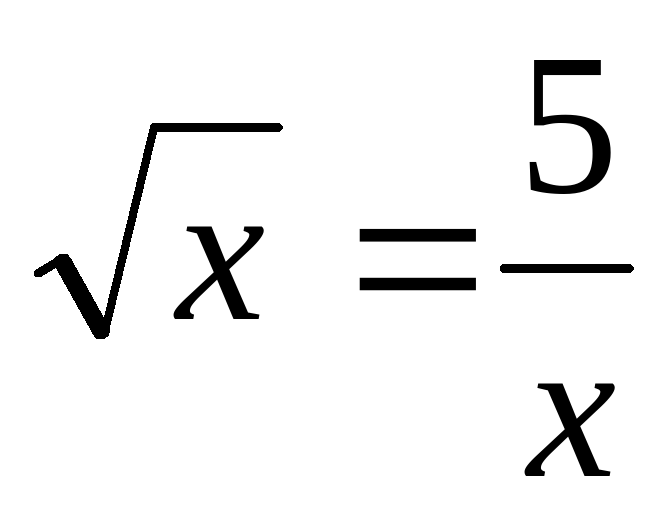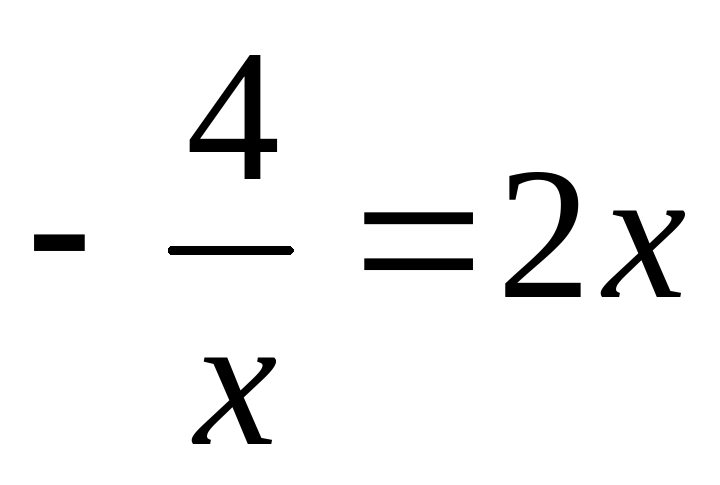1) 2) 3)

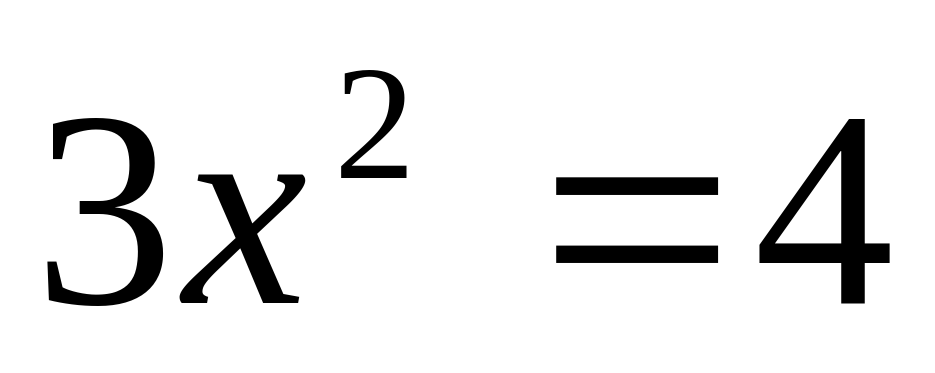
II.Решите графически уравнение:

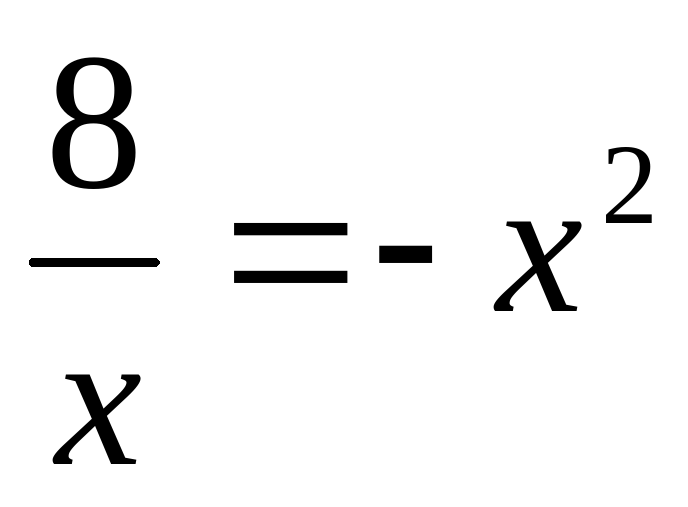
III. Выберите верный ответ:

1)На рисунке изображен график функции вида у=kx+m.

Определите знаки k и m.

А) k0; m0 Б) kmm0

2)Укажите график функции убывающей на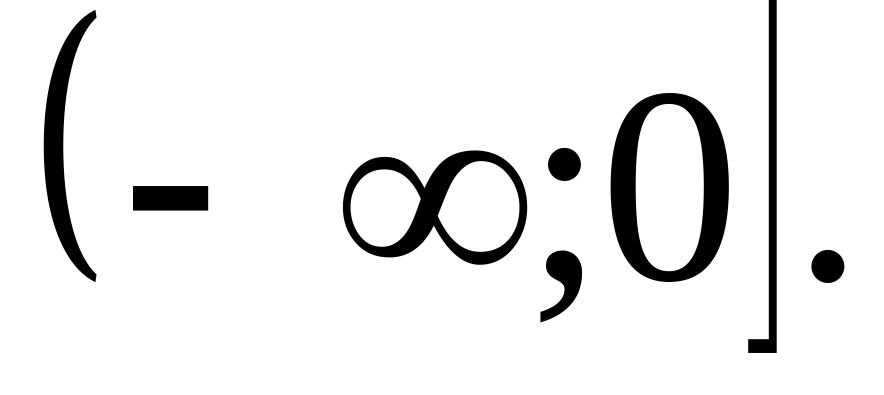

3)Укажите график функции ограниченной снизу.

4)Дан график функции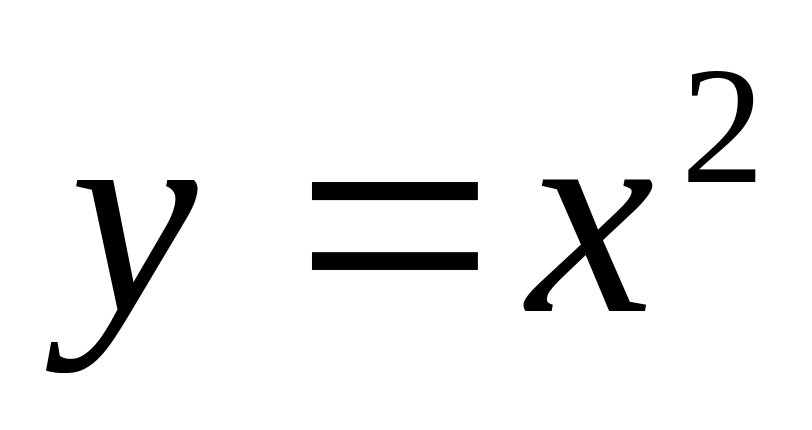 . Какие из утверждений верны?

1.Функция ограничена сверху.

2.

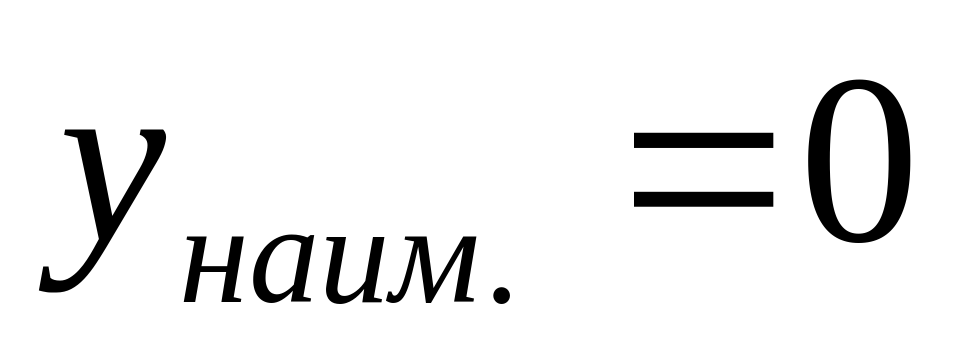
3.Выпукла вверх.

4.Непрерывна.

А) 2 и 4 Б) 1 и 2 В) 2 и 3

IV. Постройте график функции: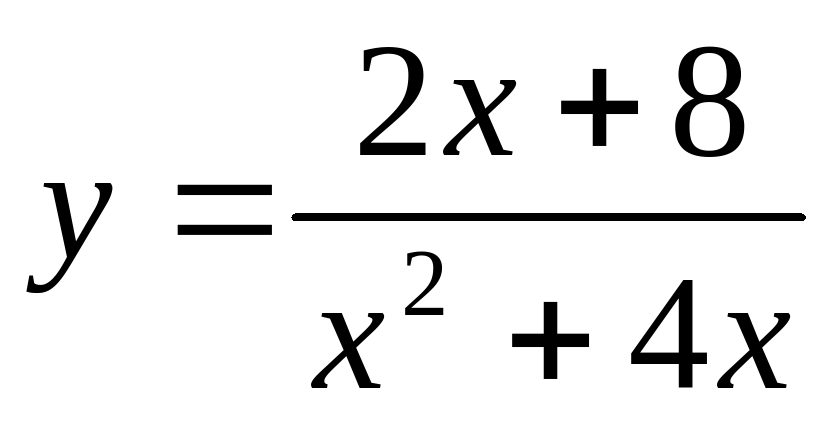

Дополнительные задания:

V. Дана функция у=f(х), где f(х)=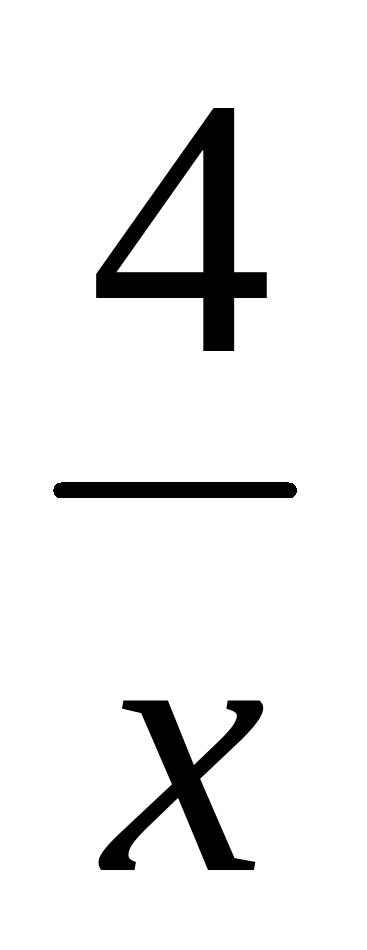 . Решите уравнение

f(x-1)-f(x+1)=1.

VI. Постройте графики функций:

а) ;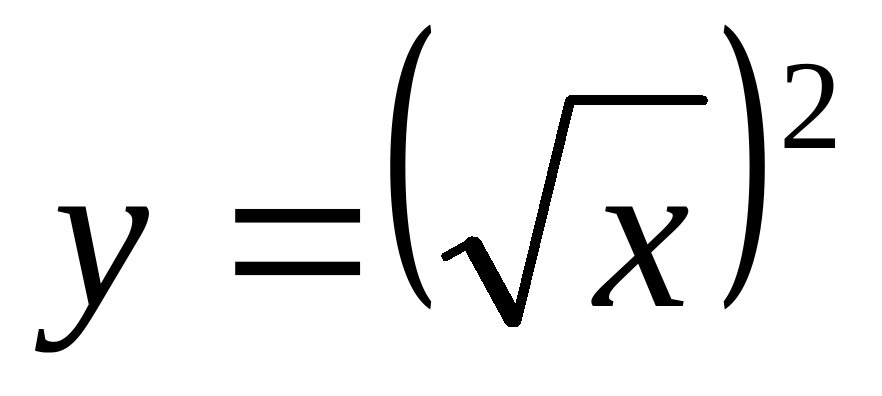

б)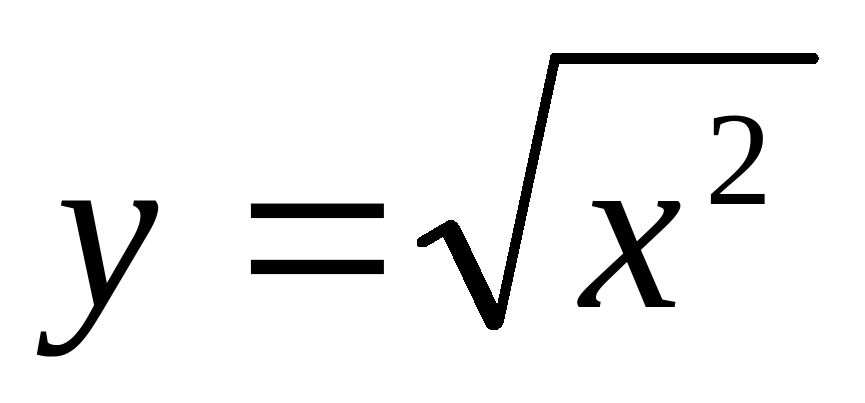

Список литературы

1.Мордкович А.Г. Алгебра. 9 кл.: В двух частях. – М.: Мнемозина, 2008.

2.Программы. Математика.5-6 классы. Алгебра.7-9 классы. Алгебра и начала анализа. 10-11 классы./авт.-сост. И.И.Зубарева, А.Г.Мордкович. – М.: Мнемозина, 2007.

3.Мордкович А.Г., Тульчинская Е.Е. Алгебра: Тесты для 7-9 кл. общеобразоват. учреждений. - М.: Мнемозина, 2000.

4.Глайзер Г.Д. Повышение эффективности обучения математике в школе. - М.: Просвящение,1989.

5. Мордкович А.Г. Алгебра. 7-9 кл.: Методическое пособие для учителя. – М.: Мнемозина, 2001.

Функции и их графики подготовка к ОГЭ по математике 9 кл

а)у= IxI б)у=кх+ m в)у=√х г)у=кх д)у=кх е)у=

к

2

х

у

у

у

2)

1)

3)

х

х

х

0

0

0

у

у

у

5)

6)

4)

х

х

х

0

0

0

2)Найдите наименьшее и наибольшее значения функции у=2х на

2

-1;2

у

8

-2

х

0

-1

2

0 ; б)у у х 0" width="640"

3)При каких значениях х: а)у 0 ; б)у

у

х

0

4)Определите промежутки монотонности функции у= IxI

y

x

0

5) Принадлежат ли графику функции у=√х данные точки?

А(-4;-2) В(2;4) С(0,01;0,1)

6)При каком значении к график функции у=кх проходит через точку М(2;20)?

2

1)у=-3х 2)у=-√х 3)у=- IxI 4)у=3х-1 5)у=-2х 6)у=0,5х 7)у=

4

2

х

у

у

у

у

н

б

л

й

х

х

х

х

0

0

у

у

у

ц

е

и

х

х

х

0

0

0

Л е й б н и ц

Вильгельм Лейбниц

(1646-1716)

«функция»

от латинского functio - совершение, выполнение

1673 год

у

у

1

1)

нет

2)

у=√х

У=2х

х

х

0

0

4

5

У=-

У=

х

х

у

2

У=3х

У=4

2

3)

х

0

3

=х-2

х

у

-3

-2

-1

-1

-1,5

-3

1

3

2

3

1,5

1

х

3

обратная пропорциональность

У=

х

х

0

у

2

-2

0

У=х-2

линейная функция

у

У=х-2

1

-1

1

х

0

3

3

Проверка:

У=

х

3

-3=-3

=-1 – 2;

-3

-1

3

=3-2; 1=1

Ответ:-1;3.

3

8

2

=-х

х

х

у

-4

-2

-2

-1

-4

-8

1

8

2

4

4

2

обратная пропорциональность

8

У=

х

х

у

-2

-4

-1

0

-1

0

1

-1

2

-4

2

У=-х

квадратичная функция

у

8

У=

х

1

1

-2

х

0

Проверка:

2

8

= -(-2)

; -4=-4

-2

-4

Ответ: -2.

2

У=-х

с

s

у

2)

3)

1)

v

д

0

0

0

с

2

2х+8

2х+8

2(х+4)

=

;

У=

=

2

Х(х+4)

х

2

Х +4х

Х +4х

2

у

; х =0 ; х=4

У=

х

х

1

-4

1

0

2

У=( √х )

2

У= √х

у

у

х

х

0

0

2

2

(√х)

√ х

= IxI

= х; х ≥0

у

2

У=(х+6)

2

У=х

1

х

1

-6

0

у

2

У=х

2

5

У=(х-6)+5

1

х

6

1

0