Занятие по рабочей программе №06
Дисциплина: БД.08 «Информатика»
Раздел 1. Информация и информационная деятельность человека.
Тема: Практическая работа №2. Системы счисления.
Цель занятия: Дидактическая:
сформулировать представление студентов об информации и информационных процессах и системах счисления;
выяснить способы перевода из одной системы счисления в другую;
определение объемов различных носителей информации;
систематизировать и обобщить знания по хранению информационных объектов на различных цифровых носителях;
углубить и закрепить знания по дисциплине «Информатика».
Воспитательная:
развивать коммуникативные способности;
развивать аналитические способности;
развивать творческий подход к процессу обучения.
воспитывать самостоятельность, дисциплинированность;
стимулировать студентов к изучению дисциплины;
побуждать к формированию активной жизненной позиции;
прививать уважение и любовь к будущей профессии.
Вид занятия: практическое занятие.
Тип занятия: обобщение и систематизация знаний.
Форма проведения занятия: репродуктивная и эвристическая беседа.
Междисциплинарные связи:
Обеспечивающие Математика, Охрана труда, Безопасность жизнедеятельности.
Обеспечиваемые
Информационные технологии в профессиональной деятельности, и др.
Методическое обеспечение: опорный конспект.
Литература:
Е.В. Михеева, О.И. Титова, Информатика Учебник 6-е издание М., Издательский центр «Академия», 2011 г.
ХОД ЗАНЯТИЯ
Ознакомление с темой, целью и планом занятия.
Тема: Системы счисления.
Цель работы: научиться использовать и определять объём различных носителей информации.
ПЛАН
Понятие о системах счисления. Позиционные и непозиционные системы счисления.
Двоичная, восьмеричная и шестнадцатеричная системы счисления.
Изложение и изучение нового материала, практическое занятие.
ЛИТЕРАТУРА: [4], стр.
Понятие о системах счисления
Системой счисления называется совокупность приемов наименования и записи чисел.
Система счисления - это способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.
В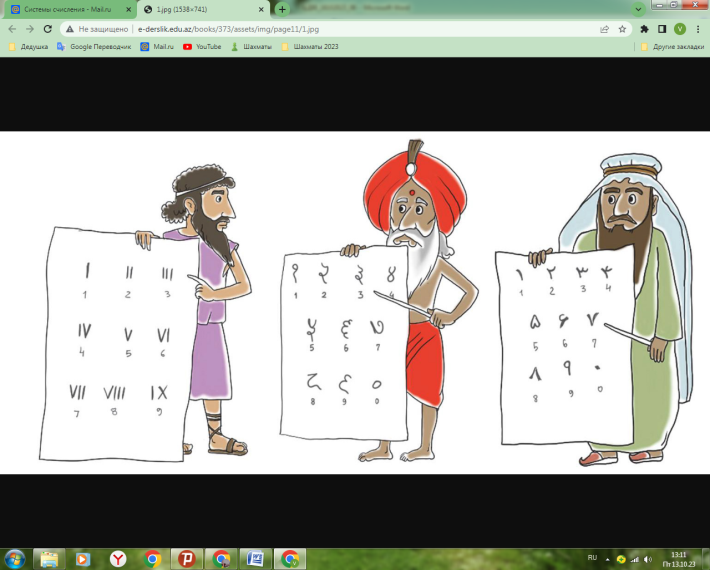 любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно.
любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно.
В современном мире наиболее распространенным является представление чисел посредством арабских цифр 0, 1,2, 3, 4, 5, 6, 7, 8, 9 - специальных знаков, используемых для записи чисел. Системы счисления различаются выбором базисных чисел и правилами образования из них остальных чисел.
Позиционные и непозиционные системы счисления
Существуют позиционные и непозиционные системы счисления. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. В позиционной системе счисления представления чисел далеко не так просты и очевидны, как в «римской» системе счисления, систематичность представления, основанная на «позиционном весе» цифр, обеспечивает простоту выполнения операций умножения и деления.
В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. В «римской» системе счисления каждый числовой знак в записи любого числа имеет одно и то же значение, т.е. значение числового знака не зависит от его расположения в записи числа. В римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти, а I – это единица.
Для изображения чисел в настоящее время используются в основном позиционные системы счисления. Привычной для всех является десятичная система счисления. В этой системе для записи любых чисел используется только десять разных знаков (цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры введены для обозначения первых десяти последовательных чисел, а следующее число 10 и т.д. обозначается уже без использования новых цифр. Однако введением этого обозначения сделан важный шаг в построении системы счисления: значение каждой цифры поставлено в зависимость от того места, где она стоит в изображении числа.
Десятичная запись любого числа X в виде последовательности цифр: 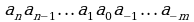 , основана на представлении этого числа в виде полинома:
, основана на представлении этого числа в виде полинома:
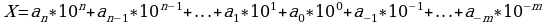 ,
,
где каждый коэффициент аi, может быть одним из чисел, для обозначения которых введены специальные знаки. Запись числа X в формуле представляет собой просто перечисление всех коэффициентов этого полинома. Точка, отделяющая целую часть числа от дробной, служит для фиксации конкретных значений каждой позиции в этой последовательности цифр и является началом отсчета.
Количество К различных цифр, употребляющихся в позиционной системе счисления, называется ее основанием системы счисления, а сама система счисления называется К - ичной. Например, основанием десятичной системы счисления является число 10; двоичной - число 2; троичной - число 3 и т.д. Для записи произвольного числа в K-ичной системе счисления достаточно иметь К разных цифр 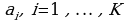 . Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.
. Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.
Запись произвольного числа X в K-ичной позиционной системе счисления основывается на представлении этого числа в виде полинома:
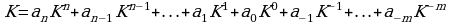 ,
,
где каждый коэффициент а, может быть одним из базисных чисел и изображается одной цифрой. В качестве базисных чисел берутся последовательные целые числа от 0 до К-1 включительно.
Позиции цифры, отсчитанные от запятой (точки), отделяющей целую часть от дробной, называются разрядами. В позиционной системе счисления вес каждого разряда больше соседнего в число раз, равное основанию системы К.
Пример: Для десятичной системы счисления (основание К=10) имеем число 6321.564. Веса разряда и коэффициенты, а для этого числа будут следующими:
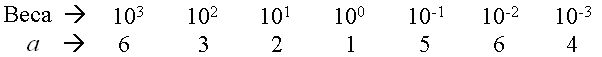
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами. Нужно только пользоваться теми таблицами сложения и умножения, которые имеют место при данном основании К системы счисления. Во всех позиционных системах счисления с любым основанием К умножения на числа вида Кm , где m - целое число, сводится просто к перенесению запятой у множимого на m разрядов вправо или влево (в зависимости от знака m), так же как и в десятичной системе.
Для указания того, в какой системе счисления записано число, условимся при его изображении основание системы счисления указывать в виде нижнего индекса при нем, например, 35,648 или подстрочным индексом, заключенным в круглые скобки, например: 1101(2).
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвижением цифры называют замену её следующей по величине.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета:
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
В настоящее время в ЭВМ применяют двоичную, восьмеричную и шестнадцатеричную системы счисления. Рассмотрим их подробнее.
Двоичная, восьмеричная и шестнадцатеричная системы счисления
Двоичная система счисления
В современной вычислительной технике, в устройствах автоматики и связи широко используется двоичная система счисления. Это система счисления с наименьшим возможным основанием. В ней для изображения числа используются только две цифры: 0 и 1. Двоичная система счисления имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток - нет тока, намагничен - не намагничен и т.п.), а не, например, с десятью, - как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы - быстрый рост числа разрядов, необходимых для записи чисел, т.е. в громоздкости записи чисел, но это не имеет существенного значения для ЭВМ. Однако если возникает необходимость кодировать информацию «вручную», например, при составлении программы на машинном языке, то предпочтительнее оказывается пользоваться восьмеричной или шестнадцатеричной системой счисления.
Как и в десятичной, в двоичной системе счисления для отделения целой части от дробной используется точка. Значение веса разрядов справа от точки равно основанию двоичной системы (2), возведенному в отрицательную степень. Такие веса - это дроби вида: 1/2, 1/22, 1/23, 1/24, 1/25 или 1/2, 1/4, 1/8, 1/16. Их можно выразить через десятичные дроби: 2-1 = 0.5, 2-2 = 0.25, 2-3 = 0.125, 2-4 = 0,0625.
В общем случае двоичное число имеет целую и дробную части, например, 1101101.10111. Каждая позиция, занятая двоичной цифрой, называется бит. Бит является наименьшей единицей информации в ЭВМ. Наименьшим значащим битом (МЗР) называют самый младший двоичный разряд, а самым старшим двоичным разрядом - наибольший значащий бит (СЗР). В двоичном числе эти биты имеют, соответственно, наименьший и наибольший вес. Двоичное число записывают так, что старший значащий бит является крайним слева.

В
 осьмеричная система счисления
осьмеричная система счисления
В восьмеричной системе счисления базисными числами являются 0, 1, 2, 3, 4, 5, 6, 7. Запись любого числа в этой системе основывается на его разложении по степеням числа восемь с коэффициентами, являющимися указанными выше базисными числами.
Восьмеричная система счисления не нужна ЭВМ в отличие от двоичной системы. Она удобна как компактная форма записи чисел и используется программистами (например, в текстах программ для более краткой и удобной записи двоичных кодов команд, адресов и операндов).
В восьмеричной системе счисления вес каждого разряда кратен восьми или одной восьмой, поэтому восьмиразрядное двоичное число позволяет выразить десятичные величины в пределах 0-255, а восьмеричное охватывает диапазон 0 - 99999999 (для двоичной это составляет 27 разрядов).
Поскольку 8=23, то каждый восьмеричный символ можно представить трехбитовым двоичным числом.
Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число влево (для целой части) и вправо (для дробной) от точки (запятой) на группы по три разряда (триады) и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются необходимым количеством незначащих нулей.
Пример: Двоичное число 1011,01012 записать в восьмеричной системе счисления.
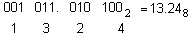
Перевод из восьмеричной системы счисления в двоичную систему осуществляется путем представления каждой цифры восьмеричного числа трехразрядным двоичным числом (триадой).
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными являются числа от нуля до пятнадцати. Эта система отличается от рассмотренных ранее тем, что в ней общепринятых (арабских) цифр не хватает для обозначения всех базисных чисел, поэтому приходится вводить в употребление новые символы. Обычно для обозначения первых десяти целых чисел от нуля до девяти используют арабские цифры, а для следующих целых чисел от десяти до пятнадцати используются буквенные обозначения A, B, C, D, E, F.
Шестнадцатеричная система счисления позволяет еще короче записывать многоразрядные двоичные числа и, кроме того, сокращать запись 4-разрядного двоичного числа, т.е. полубайта, поскольку 16=24. Шестнадцатеричная система так же применяется в текстах программ для более краткой и удобной записи двоичных чисел.
Для перевода числа из двоичной системы счисления в шестнадцатеричную, необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.
Пример: Двоичное число 10101011111101(2) записать в шестнадцатеричной системе.

Для перевода числа из шестнадцатеричной системы счисления в двоичную, необходимо наоборот каждую цифру этого числа заменить тетрадой.

Задание. Перевод чисел между двоичной, восьмеричной и шестнадцатеричной системами счисления.
1) Преобразуйте следующие двоичные числа в десятичные: 11100; 1110010; 110110.
2) Преобразуйте следующие десятичные числа в двоичные: 49; 856; 160.
3) Преобразовать свою дату рождения в различные системы счисления: ДД МЕСЯЦ ГОД
Контрольные вопросы
1. Что такое система счисления?
2. Как определяется основание системы счисления?
3. Приведите примеры позиционных и непозиционных систем счисления.
4. Двоичная, восьмеричная и шестнадцатеричная системы счисления.
5. Перевод чисел их десятичной системы счисления в 2, 8 и 16 систему счисления.
6. Сформулируйте правило счета.
7. Представление чисел в виде полинома в 2, 8, 10 и 16 системах счисления.
ДОМАШНЕЕ ЗАДАНИЕ
Составить конспект лекции
Ответить письменно на контрольные вопросы.
Выполнить Задание.
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.
Основные источники:
1. Симонович, С. В. Информатика. Базовый курс : Учебник для вузов. 3 - е изд. Стандарт третьего поколения. – СПб., 2016
2. Гохберг, Г.С. Информационные технологии : учебник для студ. сред. проф. Образования / Гохберг, Г.С, Зафиевский, А.В., Короткин, А.А.- 5-е изд., стер. – М. : Издательский центр «Академия», 2010. – 208с.
3. Филимонова, Е.В. Информационные технологии в профессиональной деятельности : учебник. – Изд-е 2-е, доп. и перераб. – Ростов н/Д : Феникс, 2008. – 381. – (СПО).
4. Е.В. Михеева, О.И. Титова Информатика Учебник 6-е издание М., Издательский центр «Академия», 2011 г
Дополнительные источники:
Колесниченко, О.В., Шишигин, И.В. Аппаратные средства PC. 5-е издание. СПб. БХВ - Петербург, 2006.
Ральф Вебер. Сборка, конфигурирование, настройка, модернизация и разгон ПК. - ДиаСофт, 2007.
Гребенюк, Е.И., Гребенюк, Н.А. Технические средства информатизации: учебник для студ. учреждений сред. проф. образования / Е. И. Гребенюк, Н.А.Гребенюк. – 9-е изд., перераб. и доп. – М. : Издательский центр «Академия», 2014. – 352 с.
Максимов, Н. В., Партыка, Т. JI., Попов, И. И. Технические средства информатизации : учебник / Н. В. Максимов, Т. JI. Партыка, И. И. Попов. — 3-е изд., перераб. и доп. — М. : ФОРУМ, 2010. — 608 с.
Гук, М. Аппаратные средства IBM PC. Энциклопедия. – СПб. : Питер, 2003. – 928 с.
Технические средства информатизации. Учебное пособие. / Составитель А.Н. Попов. – Нижневартовск : НГСГК, - 2007. – 331 с.
Интернет - источники:
Электронный учебник по информатике и информационным технологиям - http://www.ctc.msiu.ru/
Тесты по информатике - http://www.ege.ru/
Преподаватель: Владимир Александрович Волков







 любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно.
любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно.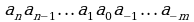 , основана на представлении этого числа в виде полинома:
, основана на представлении этого числа в виде полинома: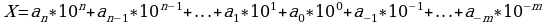 ,
,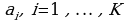 . Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.
. Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.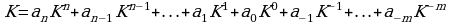 ,
,












