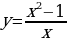Практическая работа № 35
Тема: Исследование и построение графиков элементарных функций с помощью производной.
Цель: Научится исследовать и строить графики функций с помощью производной..
Методические указания.
При исследовании и построении графиков функций можно использовать следующую схему:
Найти область определения функции.
Найти область допустимых значений
3. . Найти точки пересечения с осями координат:
а) с ОХ: решить уравнение у = 0;
б) с ОУ: решить уравнение х = 0.
4. Исследовать функцию на монотонность и экстремумы:
а) Найти производную f(х);
б) Найти критические точки функции, т. е. точки в которых производная равна нулю или не существует;
в) Исследовать знак производной в промежутках, на которые найденные критические точки делят числовую прямую. Если в некотором промежутке f '(х) 0, то функция возрастает в этом промежутке; если же f '(х)
г) Выяснить наличие экстремума в каждой критической точке 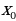 , отличной от точек разрыва функции: а) Если f '(х)
, отличной от точек разрыва функции: а) Если f '(х) 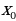 ) и f '(х) 0 на (
) и f '(х) 0 на (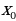 ;в), то
;в), то 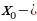 точка минимума функции
точка минимума функции
б) Если f '(х) 0 на (а;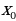 ) и f '(х)
) и f '(х) 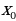 ;в), то
;в), то 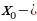 точка максимума функции.
точка максимума функции.
д) Вычислить значения функции в точках экстремума.
5. Найти точки перегиба и интервалы выпуклости графика функции.
Содержание работы.
Вариант-1
Исследуйте график функции и постройте график любой из них:
а) 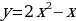 б)
б) 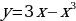 в)
в) 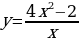
Практическая работа № 35
Тема: Исследование и построение графиков элементарных функций с помощью производной.
Цель: Научится исследовать и строить графики функций с помощью производной..
Методические указания.
При исследовании и построении графиков функций можно использовать следующую схему:
Найти область определения функции.
Найти область допустимых значений
3. . Найти точки пересечения с осями координат:
а) с ОХ: решить уравнение у = 0;
б) с ОУ: решить уравнение х = 0.
4. Исследовать функцию на монотонность и экстремумы:
а) Найти производную f(х);
б) Найти критические точки функции, т. е. точки в которых производная равна нулю или не существует;
в) Исследовать знак производной в промежутках, на которые найденные критические точки делят числовую прямую. Если в некотором промежутке f '(х) 0, то функция возрастает в этом промежутке; если же f '(х)
г) Выяснить наличие экстремума в каждой критической точке 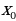 , отличной от точек разрыва функции: а) Если f '(х)
, отличной от точек разрыва функции: а) Если f '(х) 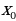 ) и f '(х) 0 на (
) и f '(х) 0 на (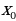 ;в), то
;в), то 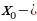 точка минимума функции
точка минимума функции
б) Если f '(х) 0 на (а;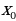 ) и f '(х)
) и f '(х) 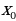 ;в), то
;в), то 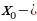 точка максимума функции.
точка максимума функции.
д) Вычислить значения функции в точках экстремума.
5. Найти точки перегиба и интервалы выпуклости графика функции.
Содержание работы.
Вариант-2
Исследуйте график функции и постройте график любой из них:
а) 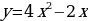 б)
б) 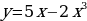 в)
в) 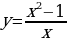






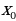 , отличной от точек разрыва функции: а) Если f '(х)
, отличной от точек разрыва функции: а) Если f '(х) 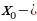 точка минимума функции
точка минимума функции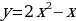 б)
б) 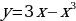 в)
в) 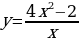
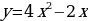 б)
б) 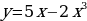 в)
в)