Практическая работа №63 «Осевое и перпендикулярное сечения цилиндра и конуса»

Практическая работа №63 «Осевое и перпендикулярное сечения цилиндра и конуса»

Цель работы: закрепить умения учащихся строить сечения конуса и цилиндра, используя свойства проекций.

Теоретические сведения к практической работе:

Сечения цилиндра: Сечения цилиндра плоскостью можно рассматривать как параллельные проекции основания цилиндра на эту плоскость. Поэтому, если плоскость параллельна плоскости основания, то в сечении получается круг, равный основанию.

Е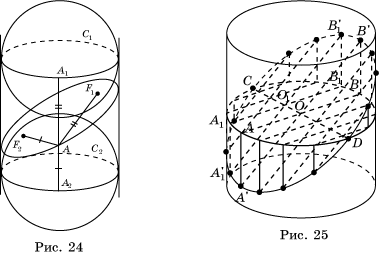 сли плоскость сечения составляет некоторый угол с плоскостью основания цилиндра и не пересекает основания, то в сечении будет фигура, ограниченная эллипсом.

На рис. показано построение точек эллипса, получающегося как сечение боковой поверхности цилиндра плоскостью.

Для этого зададим два сопряженных диаметра ABи CD. Через точку Aпроведем образующую и выберем на ней какую-нибудь точку A’, принадлежащую сечению. Прямая A’O пересечет образующую, проходящую через точку B в некоторой точке B’, также принадлежащую сечению. Возьмем теперь на отрезке CD произвольную точку и проведем через нее прямую, параллельную A’B’. Ее точки пересечения с образующими цилиндра будут принадлежать сечению.

В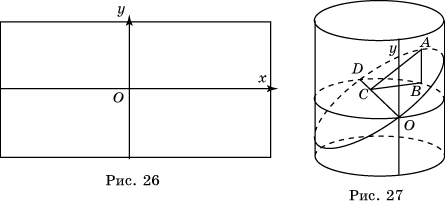 озьмем прямоугольный лист бумаги и нарисуем на нем оси координат Ox и Oy параллельно соответствующим сторонам.

З атем свернем этот лист в боковую поверхность прямого кругового цилиндра, радиус основания которого примем за единицу. Ось Ox свернется в окружность радиуса 1, а ось Oy станет образующей цилиндра.

Через диаметр OD полученной окружности проведем сечение, составляющее с плоскостью окружности угол в 30⁰. В этом случае сечением будет эллипс.

Сечения конуса:

С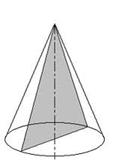 ечение конуса плоскостью, проходящей через его ось, называют осевым сечением.

( сечением является равнобедренный треугольник)

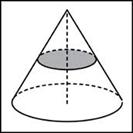
Сечение плоскостью перпендикулярной оси конуса:

(сечением является круг).

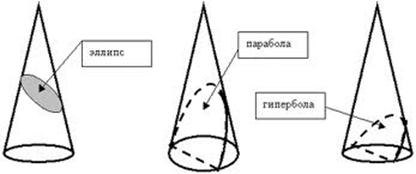
Конические сечения как результат пересечения плоскости с конусом. Возможны три основных типа конических сечений: эллипс, парабола, гипербола

Центр тяжести любого конуса лежит на четверти высоты считая от основания.

Задания для самостоятельного решения:

1) Нарисуйте цилиндр и плоскость, пересекающую его боковую поверхность по эллипсу.

2)В основании цилиндра круг радиуса 5 см. Боковая поверхность цилиндра пересечена плоскостью. Найдите площадь сечения цилиндра этой плоскостью, если она образует с плоскостью основания угол: а) 30; б) 45; в) 60.

3)  Образующая конуса, равна 8 см, наклонена к плоскости основания под углом 30о. Найдите площадь осевого сечения конуса.

Контрольные вопросы:

1. В каком случае сечением цилиндра плоскостью является круг?

2. Что будет сечением цилиндра плоскостью, проходящей через ось цилиндра?

3. Какие существуют сечения конуса?

4. Какие основные типы конического сечения существуют?