Практическая работа №64 «Решение задач на расчет площади полной поверхности конуса и усеченного конуса»

Практическая работа №64 «Решение задач на расчет площади полной поверхности конуса и усеченного конуса»

Цель работы: формирование умений и навыков при решении задач на вычисление площади поверхности конуса и усеченного конуса.

Теоретические сведения к практической работе:

К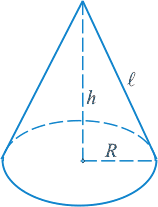 онус 

h – высота конуса, r - радиус основания, l - образующая конуса.

Площадь боковой поверхности: 

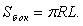
Площадь полной поверхности:

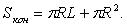
Усеченный конус

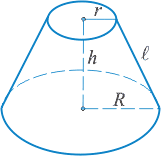
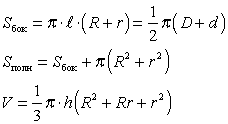
Пример 
Площадь основания конуса  36π см² , а его образующая 10 см. 
Вычислить боковую поверхность конуса. 
Решение. 
Зная площадь основания, найдем его радиус. 
S = πR² , 36π = πR² , R² = 36 , R = 6 
Площадь боковой поверхности конуса найдем по формуле: 
S = πRl , где  R - радиус основания , l - длина образующей, 
откуда 

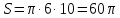
Ответ: .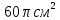

Задания для самостоятельного решения:

1.  Высота конуса равна 6, образующая равна 10. Найдите площадь боковой поверхности конуса.

2. Образующая конуса равна 18 см и наклонена к плоскости основания под углом 60°. Найдите площадь полной поверхности конуса.

3. Радиус основания конуса равен 3, высота равна 4. Найдите площадь боковой поверхности конуса.

4. Площадь осевого сечения конуса равна 0,6 см². Высота конуса равна 1,2 см. Вычислить площадь полной поверхности конуса.

5. Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите образующую усеченного конуса, площадь боковой и полной поверхности усеченного конуса.

Контрольные вопросы:

1. Как вычисляется площадь поверхности конуса?

3. Как вычисляется площадь поверхности усеченного конуса?