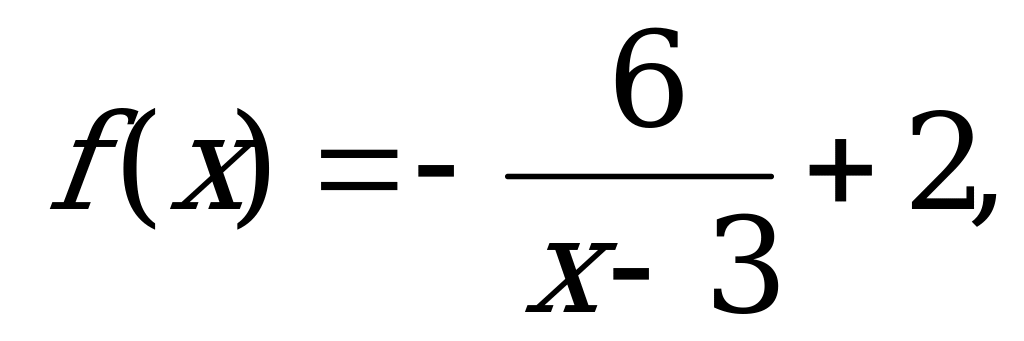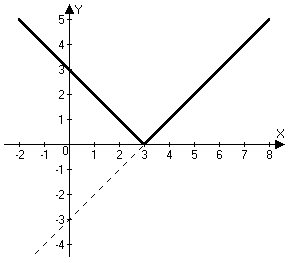Практическая работа № 3
«Функция. Свойства функций»
ЦЕЛЬ РАБОТЫ:
Корректировать знания, умения и навыки в теме: «Свойства функций».
Закрепить и систематизировать знания по теме.
Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: инструкционно-технологические карты; микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
Ответить на контрольные вопросы:
а) Что называется функцией?
б) Что такое естественная область определения функции?
в) Какая функция называется четной, нечетной?
г) Как найти точки пересечения графика функции с осями координат?
Изучить условие заданий для практической работы.
Оформить отчет о работе.
Определение функции.
Пусть Х и Y – два множества. Обозначим, через х произвольный элемент из Х, а через у – произвольный элемент из Y: 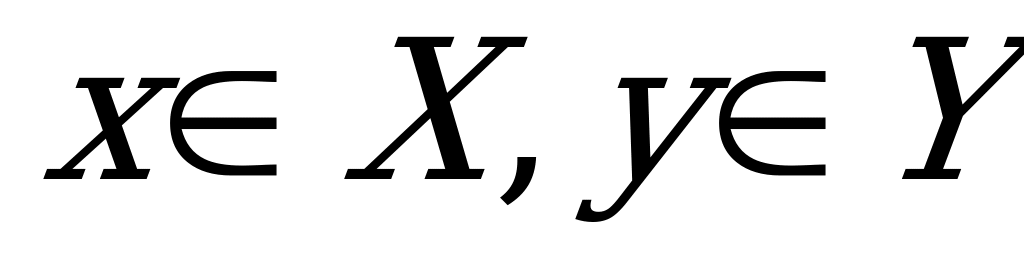 .
.
Определение 1. Отношение между элементами двух множеств Х и Y, при котором каждому элементу х первого множества соответствует один элемент у второго множества, называется функцией.
Функция, определенная на Х со значениями в Y, называется также отображением Х в Y.
Таким образом, функция и отображение означают в математике одно и то же понятие.
Отображение Х в Y обозначается обычно строчной латинской буквой, например, f,g или другими.
Пусть y есть элемент из Y, соответствующий элементу 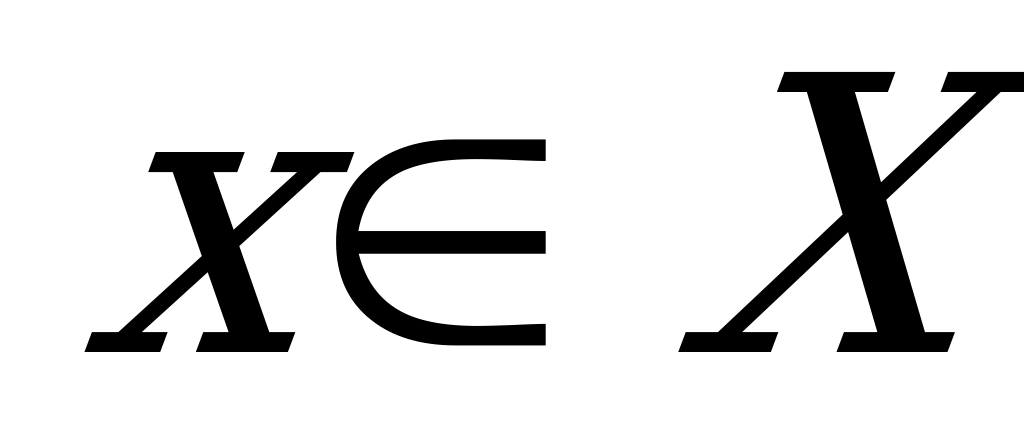 при отображении f. Это записывается так
при отображении f. Это записывается так 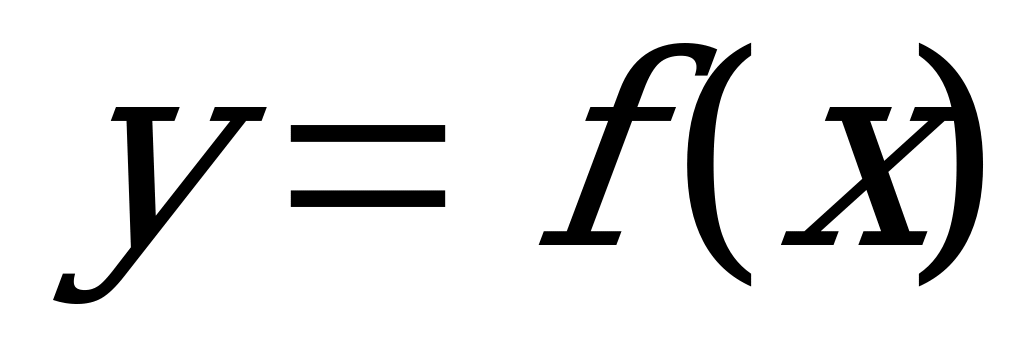 . При этом элемент y или
. При этом элемент y или 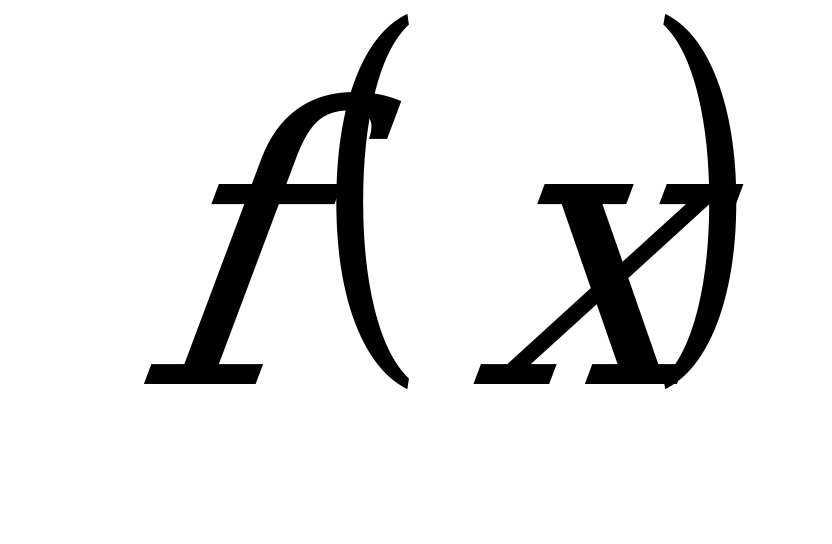 из Y называется образом элемента х при отображении f, а элемент х – прообразом элемента y при отображении f.
из Y называется образом элемента х при отображении f, а элемент х – прообразом элемента y при отображении f.
Функция обозначается 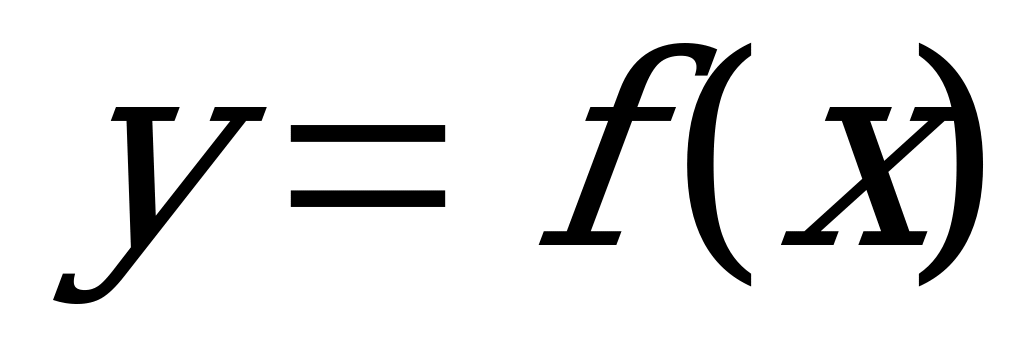 .
.
Пусть f – функция, определенная на множестве Х со значениями в Y. Из определения следует, что каждому 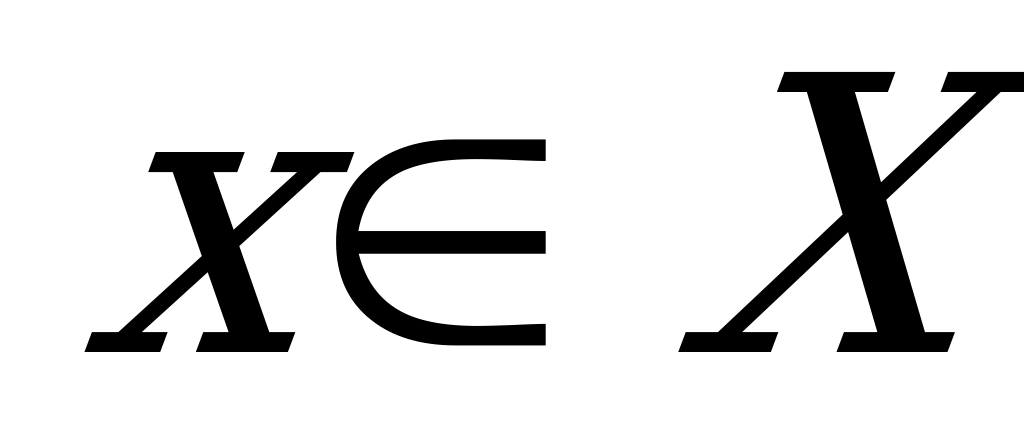 соответствует некоторый элемент из Y, в то время как множество значений
соответствует некоторый элемент из Y, в то время как множество значений 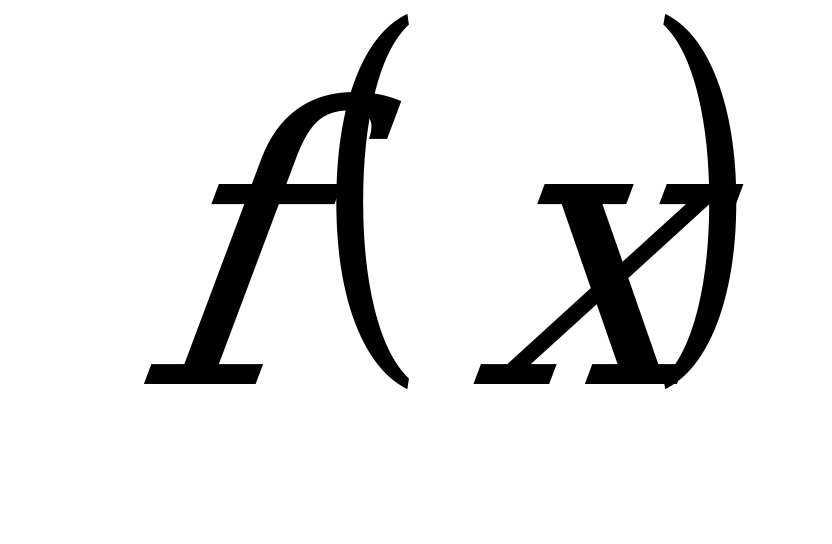 не обязательно должно совпадать с множеством Y.
не обязательно должно совпадать с множеством Y.
Переменная х - аргумент (независимая переменная),
y- функция (зависимая переменная).
Определение 2. Множество Х (множество всех значений аргумента (независимой переменной) ) называется областью определения функции и обозначается 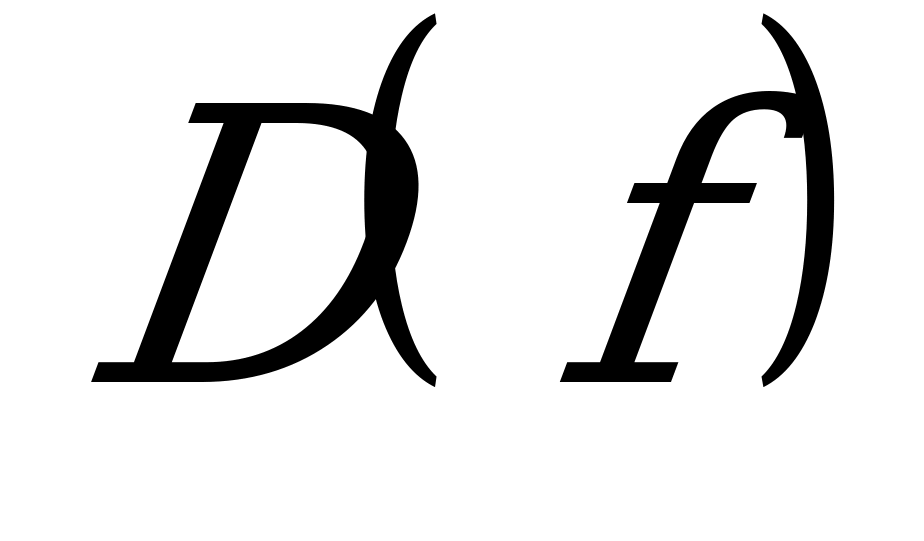 .
.
Определение 3. Множество всех y, поставленных в соответствие хотя бы одному из Х называется множеством значений функции и обозначается 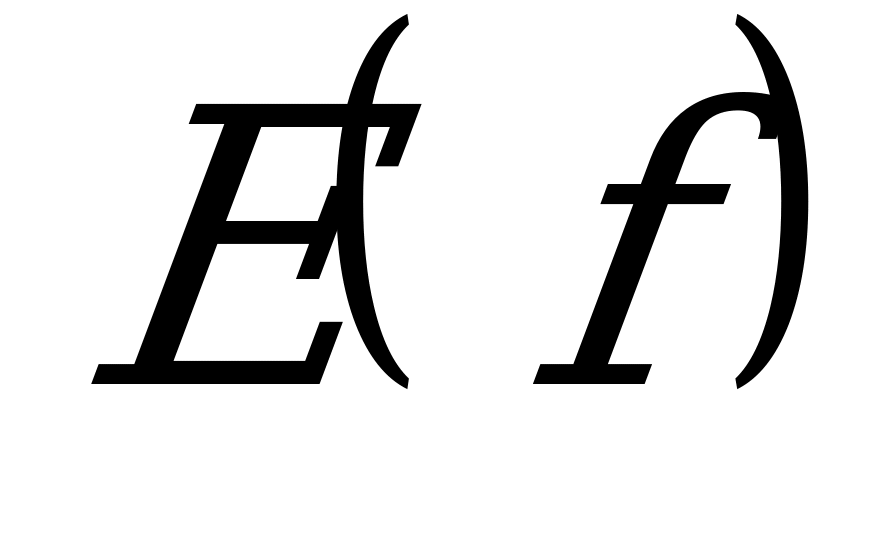 .
.
Таким образом, 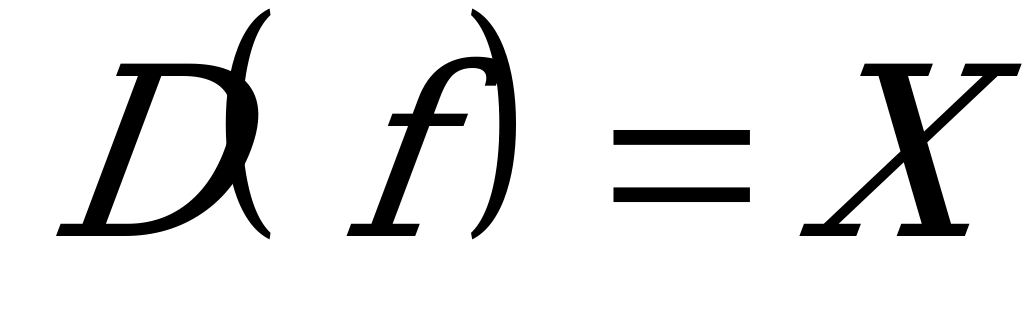 , а
, а 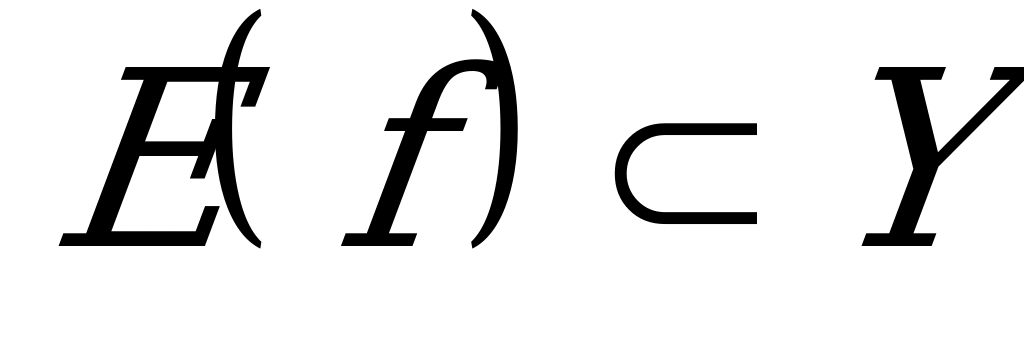 .
.
Если множество всех значений 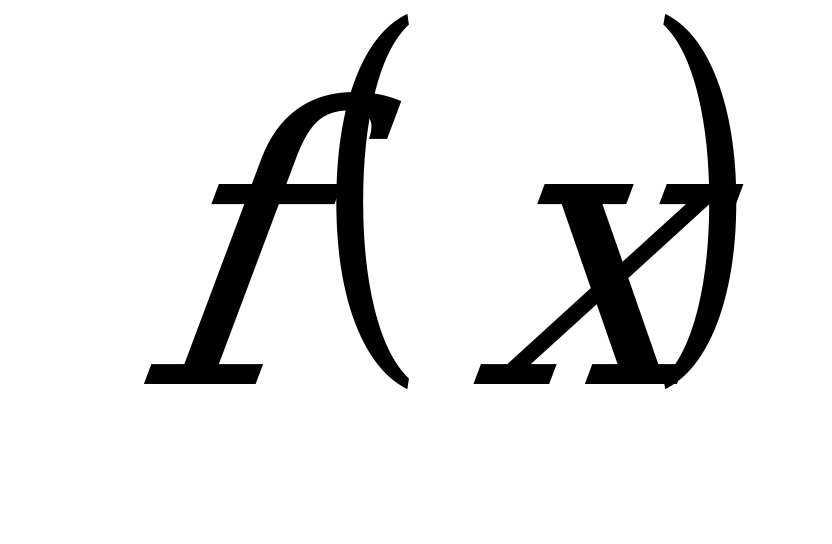 , принимаемых функцией f, есть все множество Y, т.е.
, принимаемых функцией f, есть все множество Y, т.е. 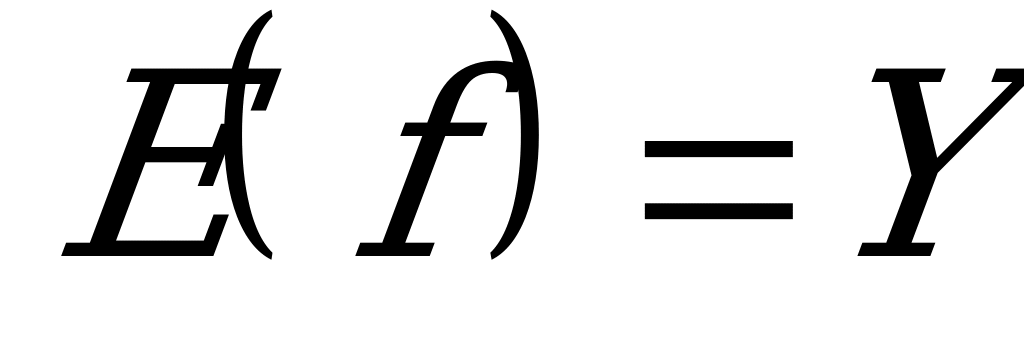 , то f называется отображением Х на Y. Следовательно, при отображении Х на Y каждый элемент
, то f называется отображением Х на Y. Следовательно, при отображении Х на Y каждый элемент 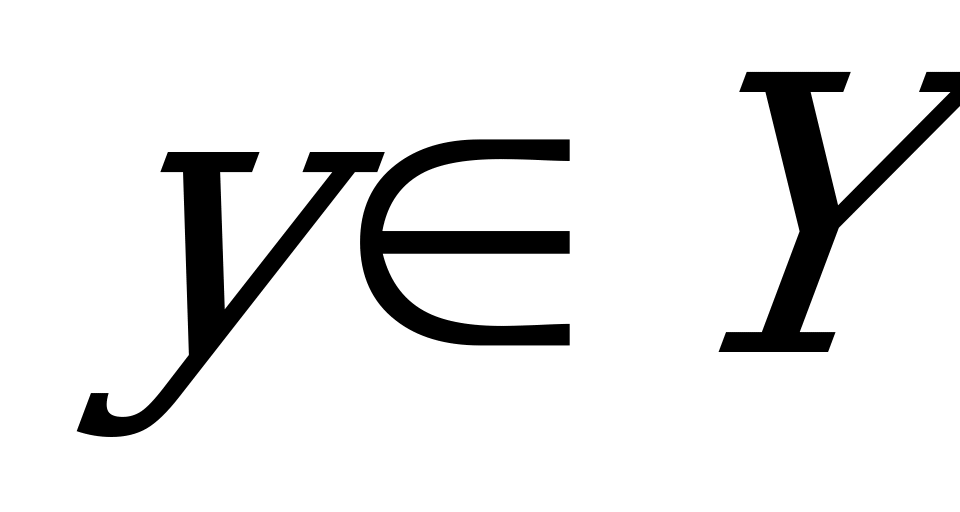 является образом хотя бы одного элемента
является образом хотя бы одного элемента 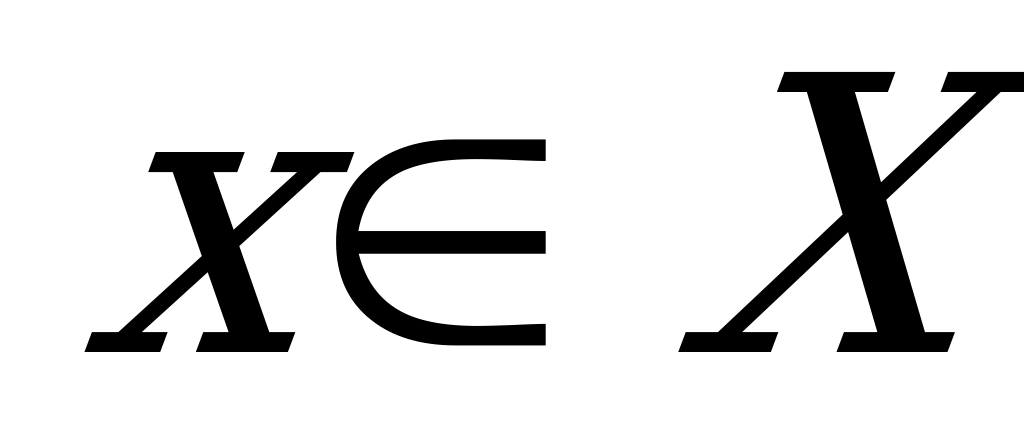 .
.
Определение 4. Отображение f называется взаимно-однозначным, если любой элемент 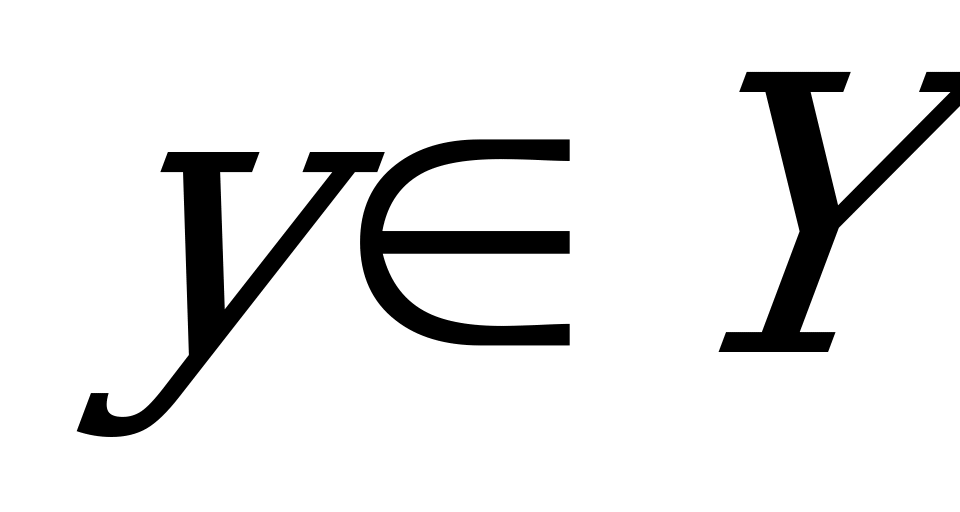 является образом единственного элемента
является образом единственного элемента 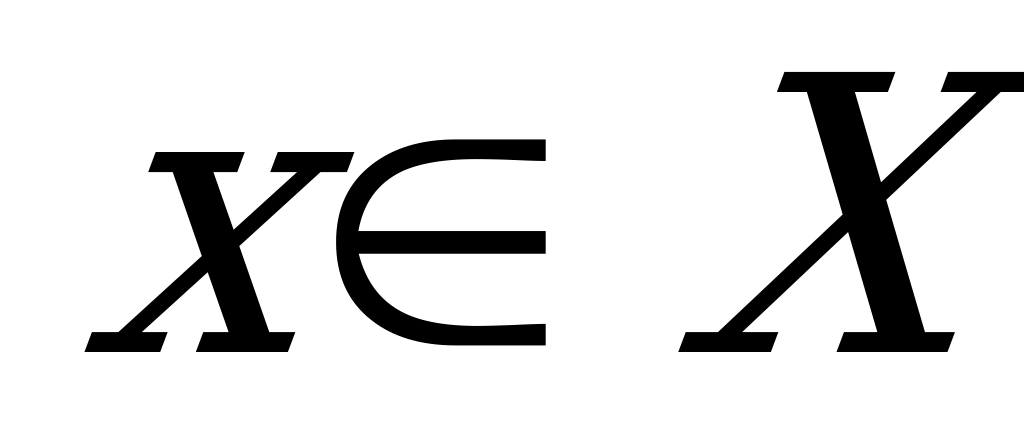 .
.
Из этого определения следует, что при взаимно-однозначном отображении каждому элементу множества Х соответствует только один элемент множества Y и, обратно, каждый элемент множества Y есть образ только одного элемента множества Х.
Рассмотрим числовые функции, т.е. отображения одного числового множества на другое числовое множество.
Определение 5. Функция, для которой область определения и область значений суть числовые множества, называется числовой функцией.
Примеры.
Найти какое значение функции соответствует числу 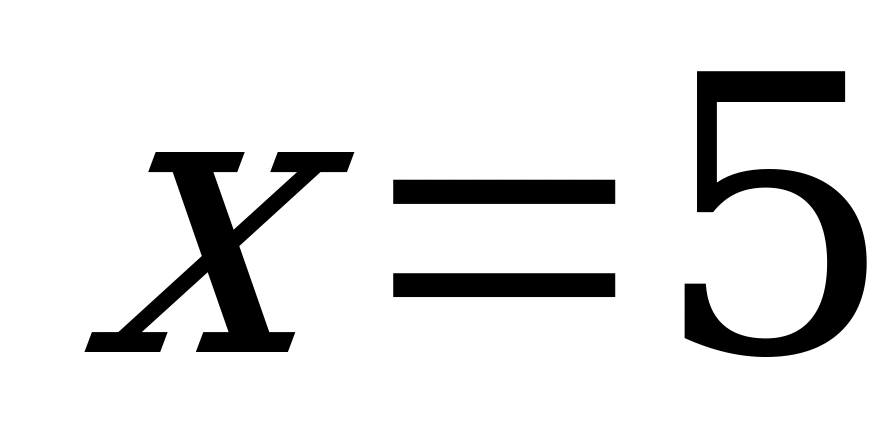 , если функция задана формулой
, если функция задана формулой 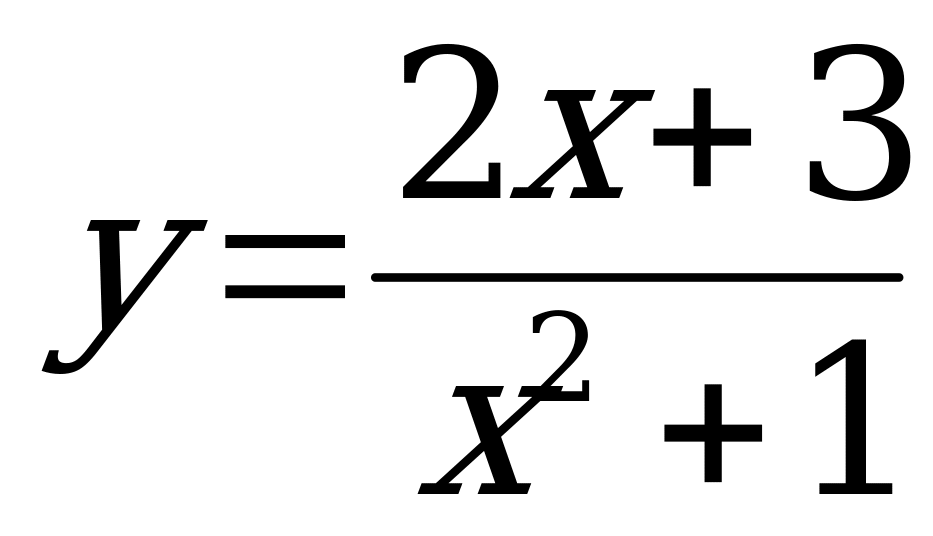 . Ответ: 0,5
. Ответ: 0,5
Найти область определения функции: а) 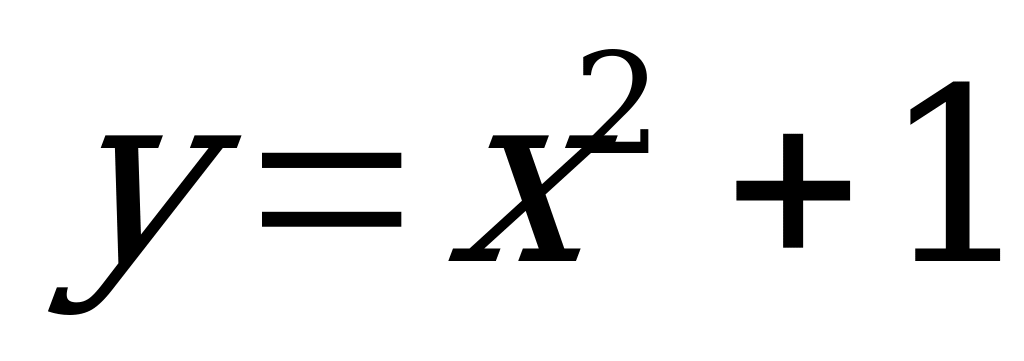 ; �
; �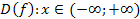 �
�
б) 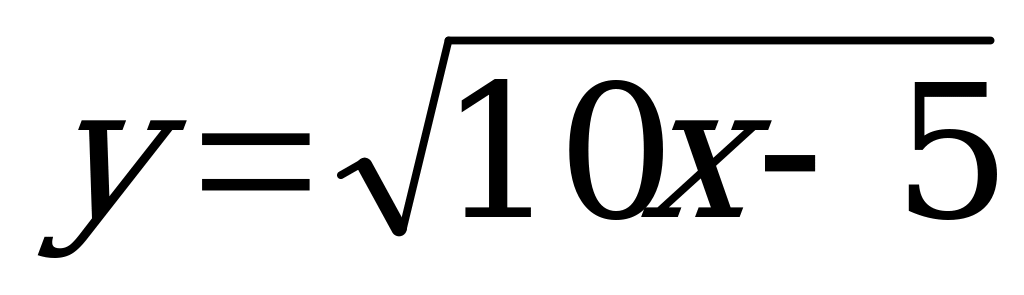 ; D(f):10x-5�
; D(f):10x-5�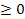 �; �
�; �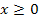 �,5 Ответ: �
�,5 Ответ: �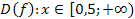 �
�
в) 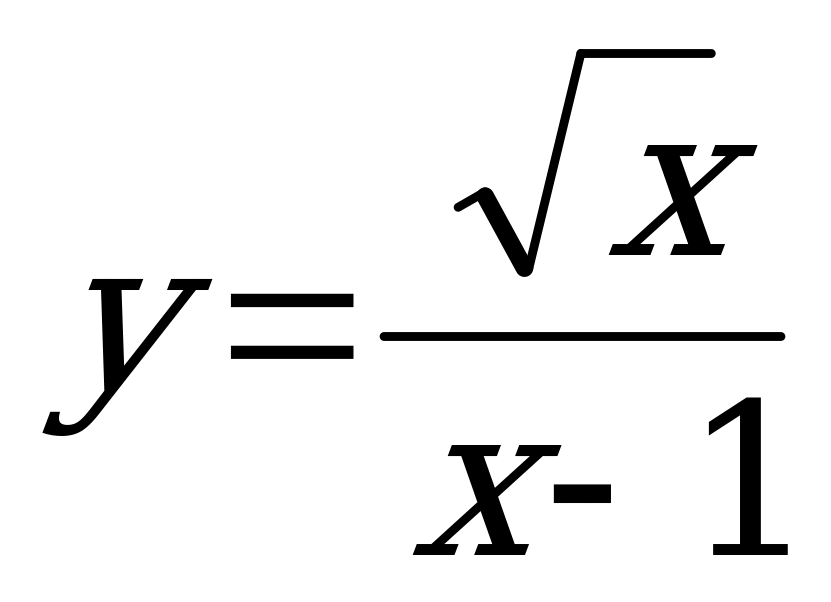 ; D(f): �
; D(f): �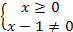 � �
� �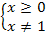 � �
� �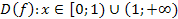 �
�
г)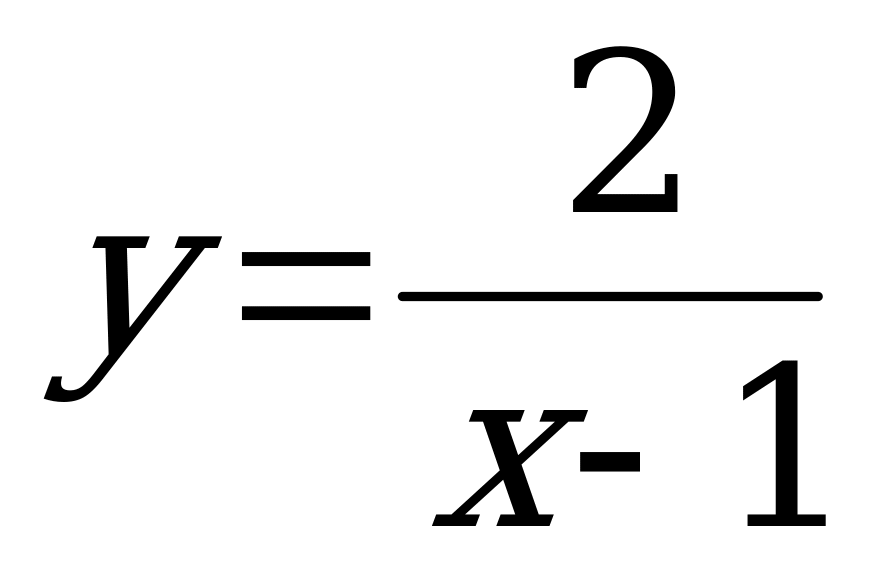 . D(f):x-1�
. D(f):x-1�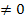 � �
� �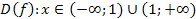 �
�
3 Свойства функции.
1) Четность и нечетность.
Определение 6. Функция f с областью определения Х называется четной, если для любого 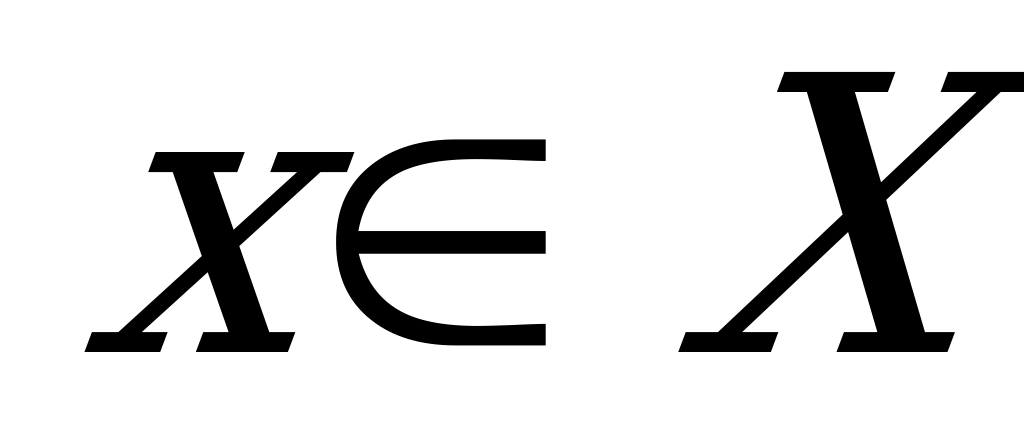 выполняется равенство:
выполняется равенство: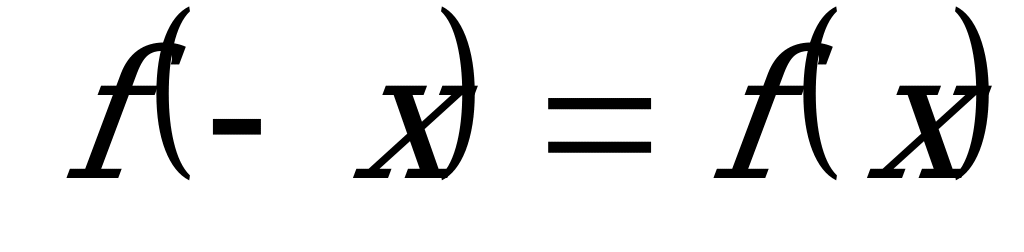 .
.
Например, 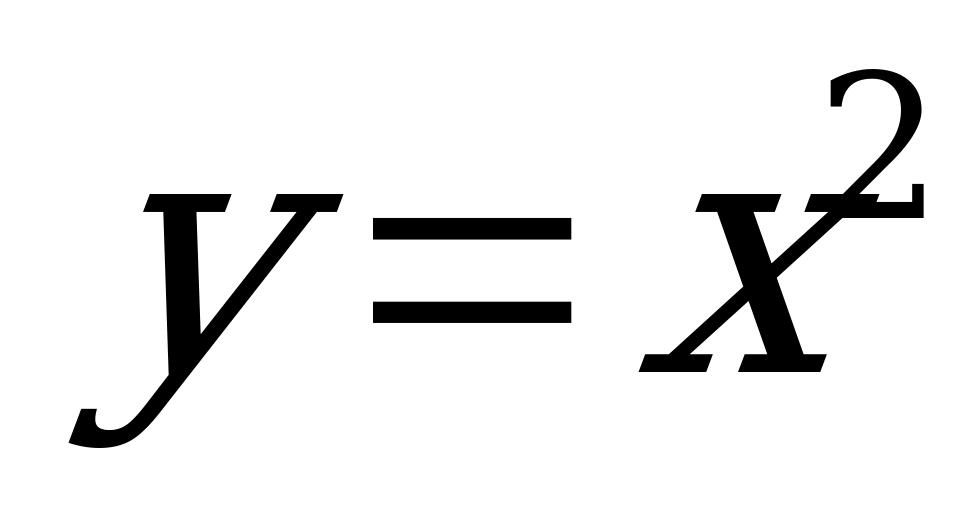 является четной.
является четной.
Замечание. График четной функции симметричен относительно оси ординат Оу.
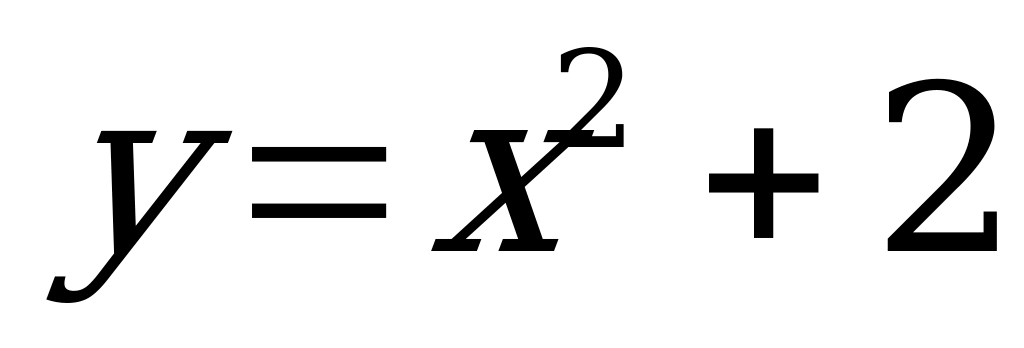 - четная функция.
- четная функция.
Определение 7. Функция f с областью определения Х называется нечетной, если для любого 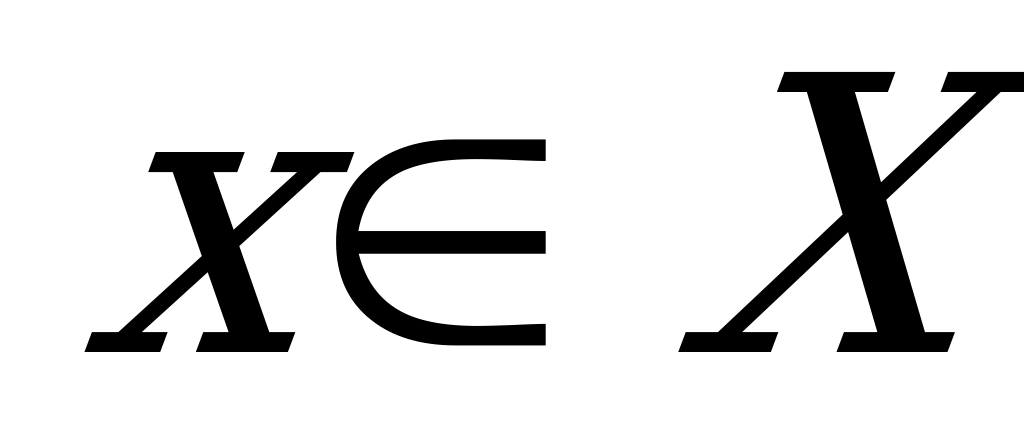 выполняется равенство:
выполняется равенство: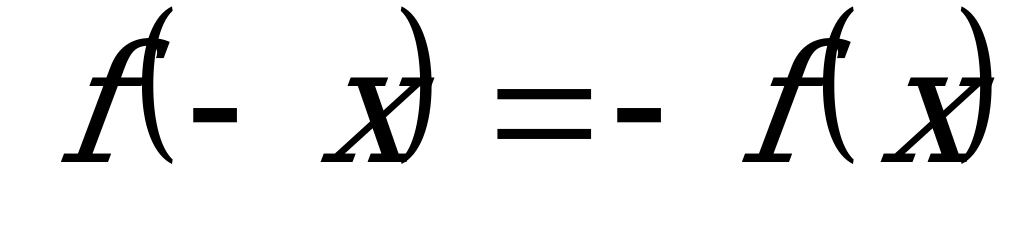 .
.
Например, 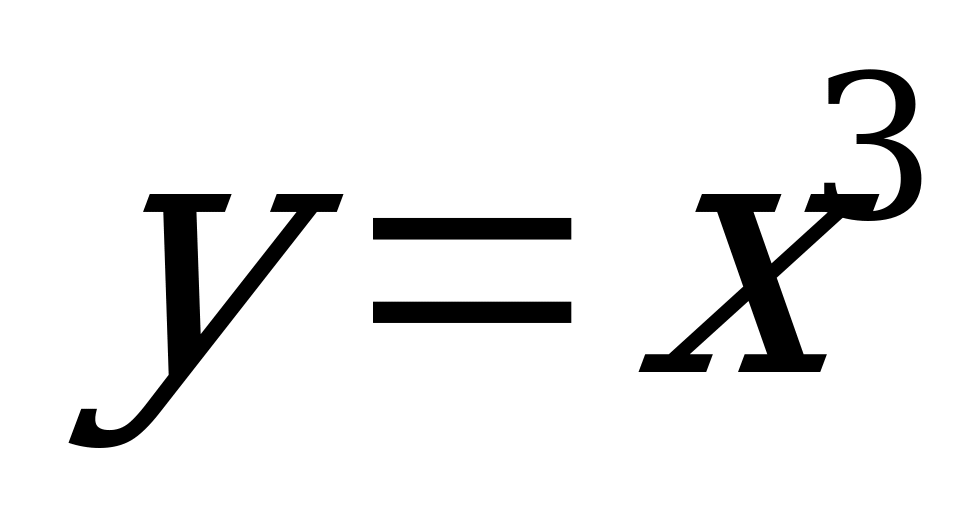 является нечетной.
является нечетной.
Замечание. График нечетной функции симметричен относительно оси начала координат О(0;0).
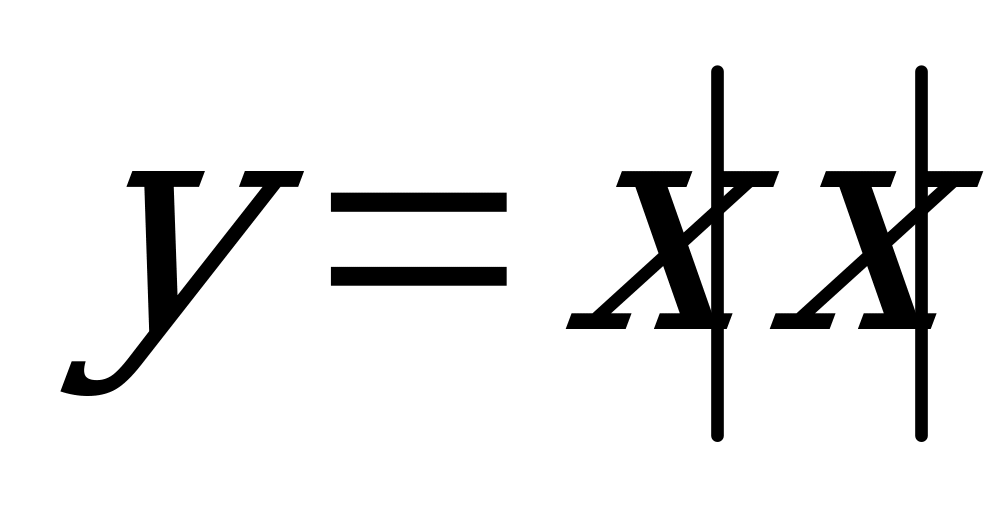 - четная функция.
- четная функция.
Какова методика определения четности – нечетности функции? Рассмотрим примеры.
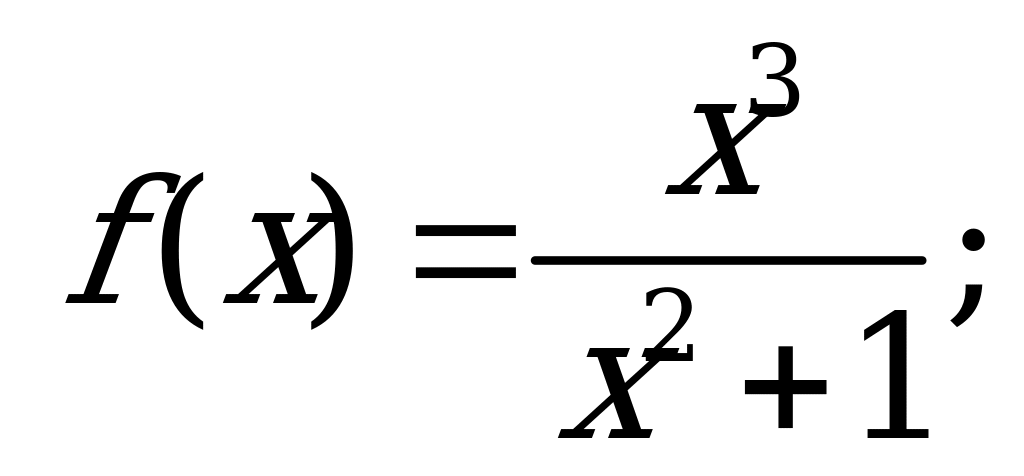 Подставим в функцию вместо x -х, будем иметь:
Подставим в функцию вместо x -х, будем иметь:
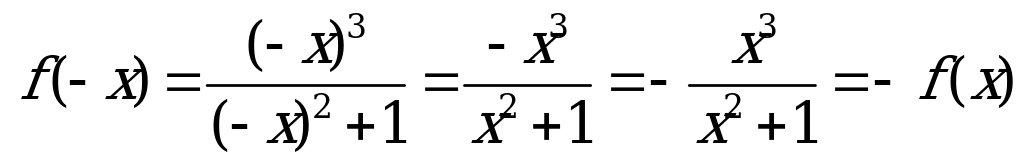 Получили определение нечетной функции, вывод: функция нечетная.
Получили определение нечетной функции, вывод: функция нечетная.
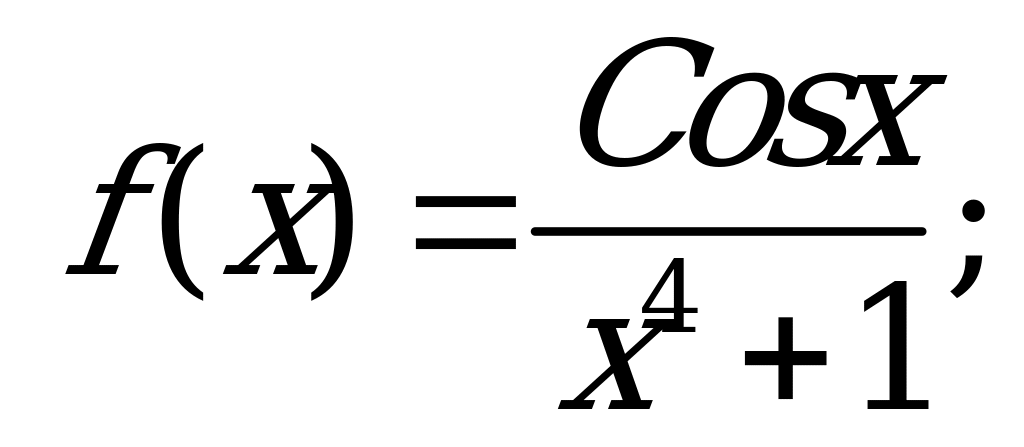 Подставим в функцию вместо х -х, будем иметь:
Подставим в функцию вместо х -х, будем иметь:
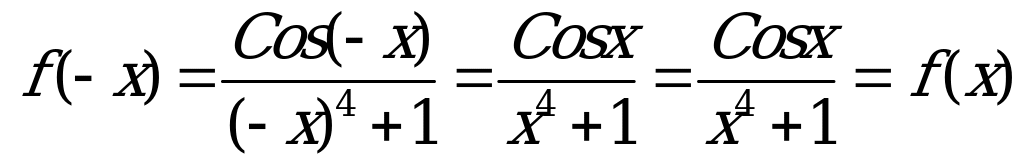 Получили определение четной функции, вывод: функция четная.
Получили определение четной функции, вывод: функция четная.
Определение 8. Функции, которые не являются ни четными ни нечетными, называются функциями общего вида.
Например, 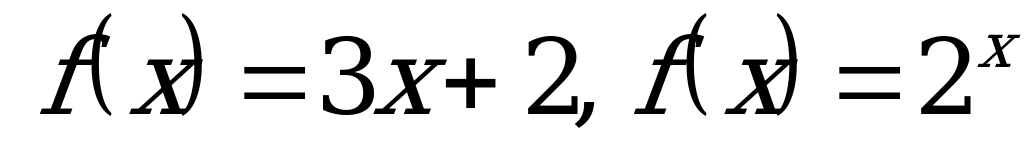 - называются функциями общего вида.
- называются функциями общего вида.
2). Периодичность.
Определение 9. Функция f с областью определения Х называется периодической, если существует такое число 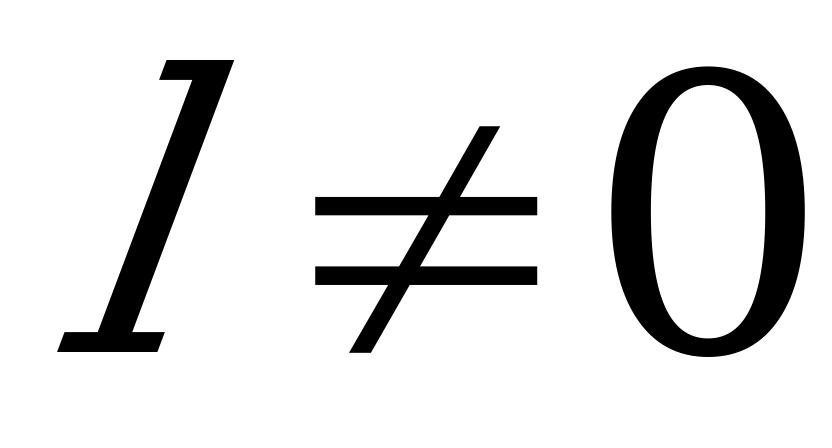 , что для любого х из множества Х выполняется равенство:
, что для любого х из множества Х выполняется равенство:
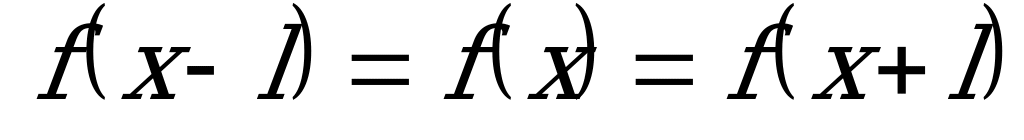 . Число l – называется периодом функции.
. Число l – называется периодом функции.
3) Монотонность.
Определение 10. Функция 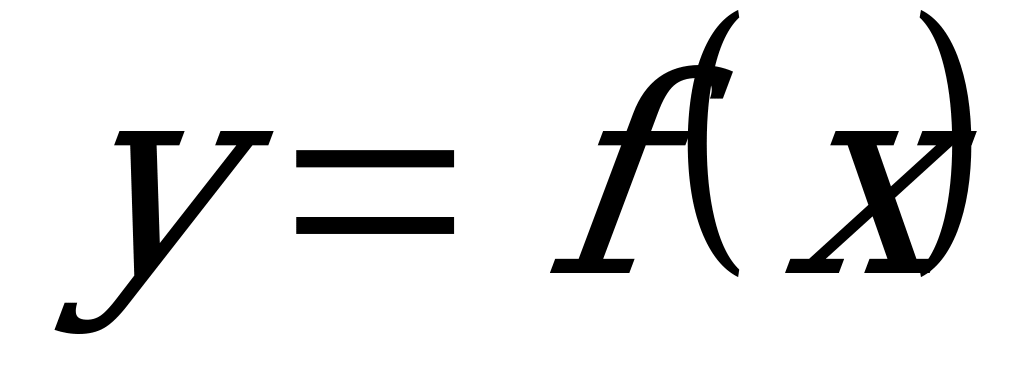 называется возрастающей (неубывающей), если большему значению аргумента x соответствует большее значение функции.
называется возрастающей (неубывающей), если большему значению аргумента x соответствует большее значение функции.
Определение 11. Функция 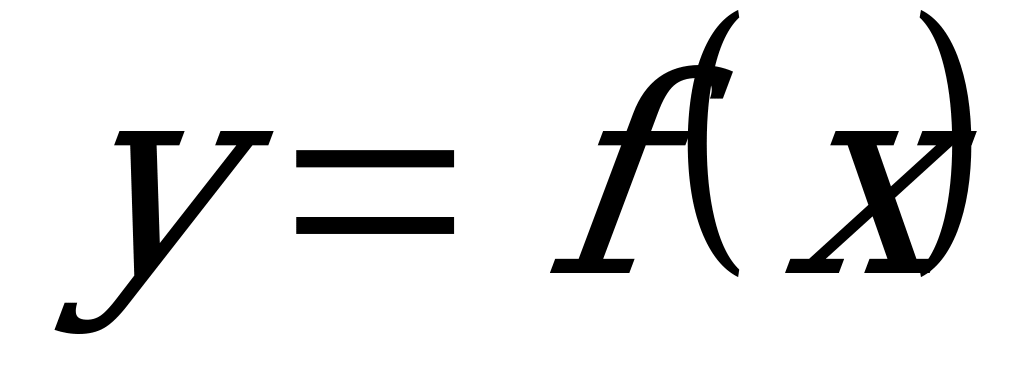 называется убывающей (невозрастающей), если большему значению аргумента xсоответствует меньшее значение функции.
называется убывающей (невозрастающей), если большему значению аргумента xсоответствует меньшее значение функции.
12. Функция называется строго монотонной, если она возрастающая или убывающая.
Определение 13. Функция называется монотонной, если она невозрастающая или неубывающая.
4. Обратная функция.
Определение. Если каждому значению функции y из множества значений 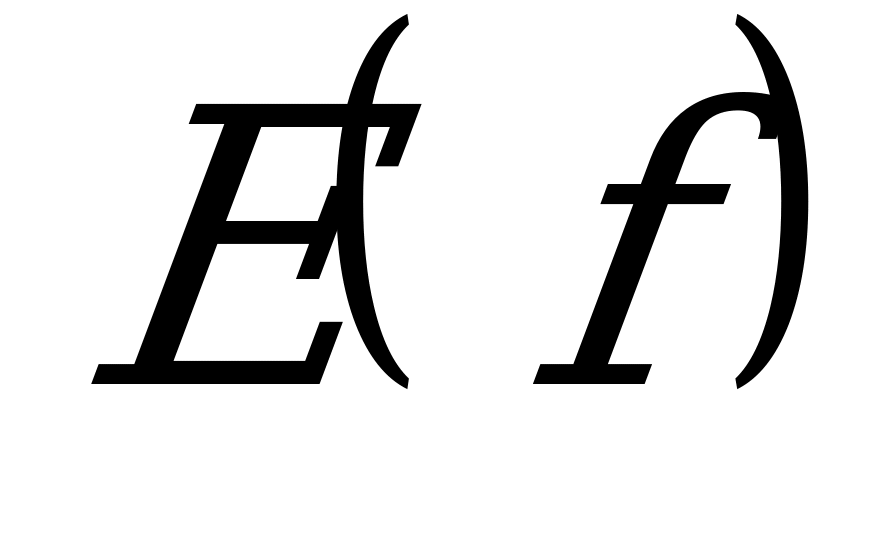 соответствует единственное значение аргумента х на области определения
соответствует единственное значение аргумента х на области определения 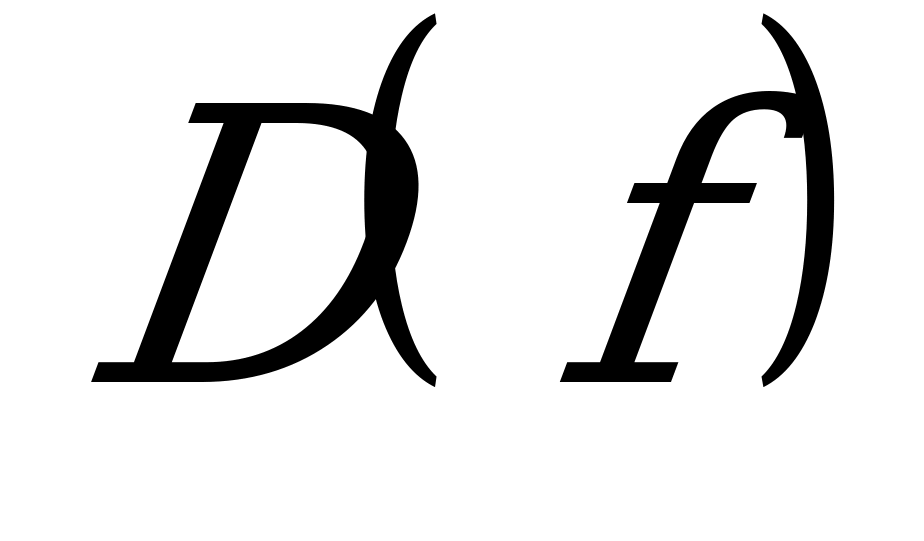 , такое, что
, такое, что 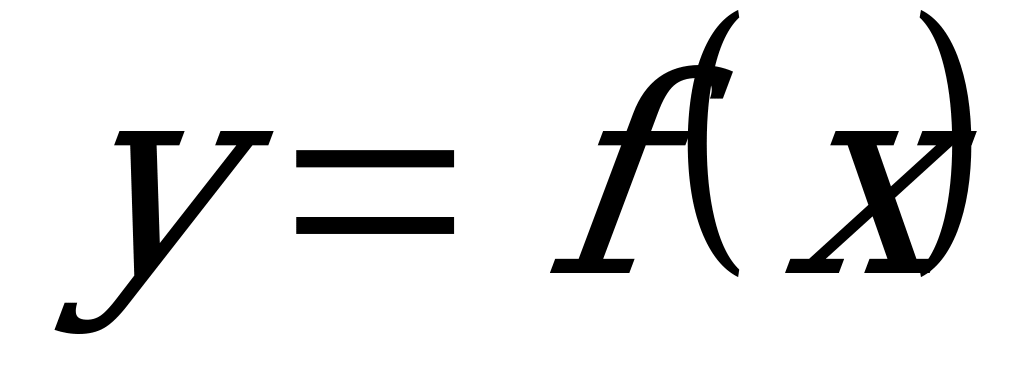 , то говорят, что функция
, то говорят, что функция 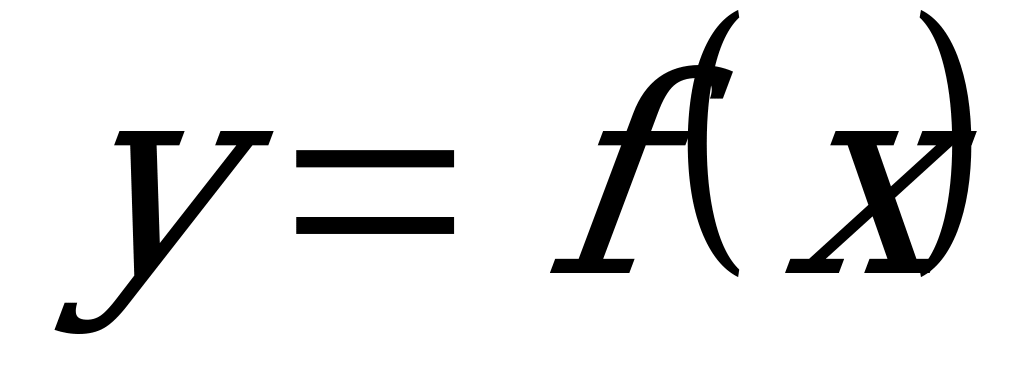 является обратимой.
является обратимой.
Определение. Если функция 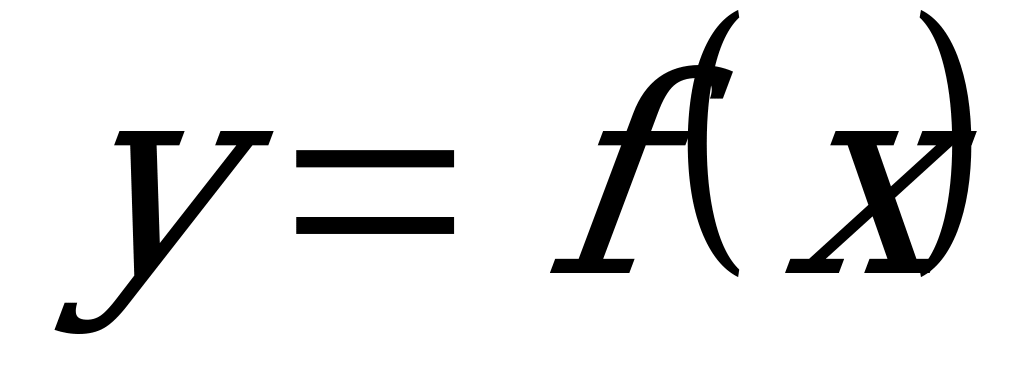 обратима, то функция
обратима, то функция 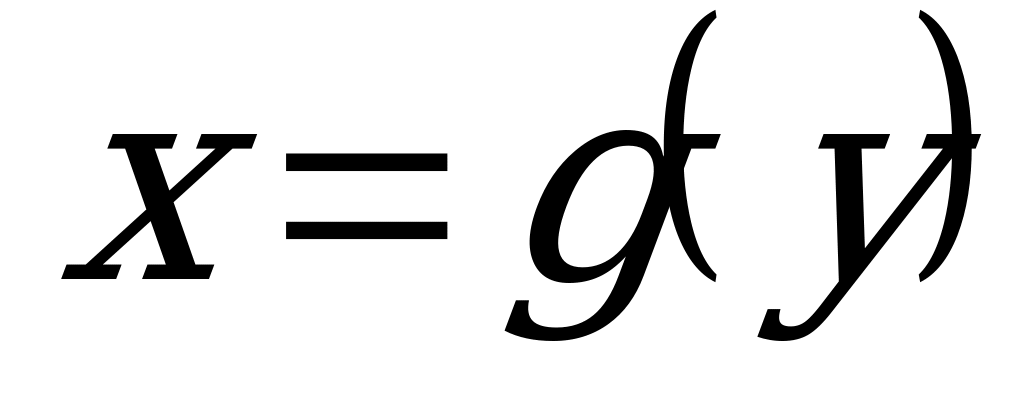 (здесь
(здесь 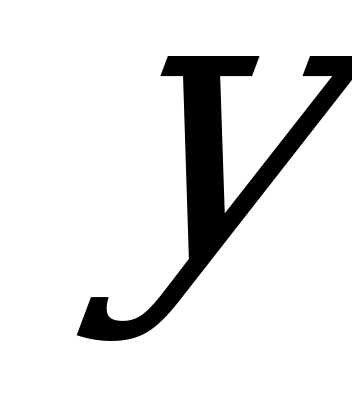 -аргумент, и х – функция) называется обратной к функции
-аргумент, и х – функция) называется обратной к функции 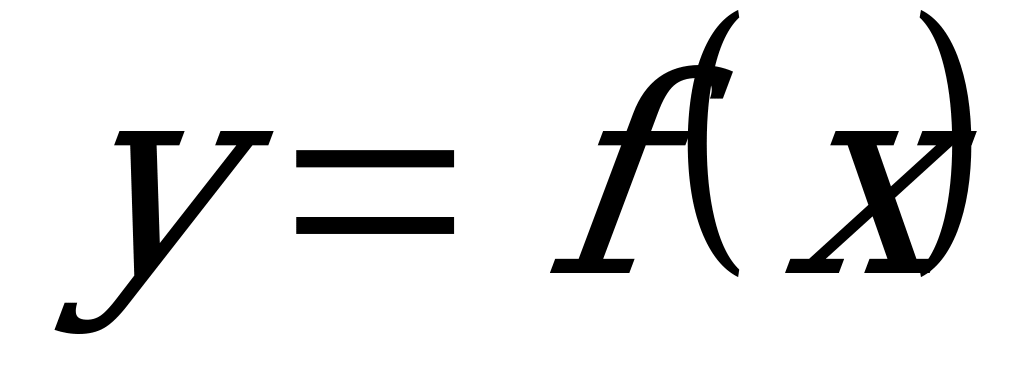 , при этом
, при этом 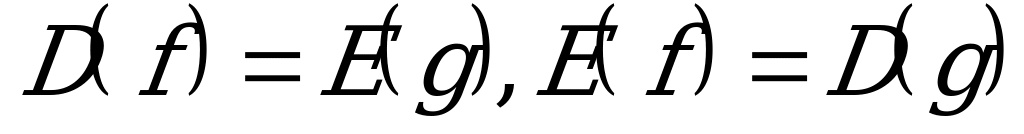 и для любых
и для любых 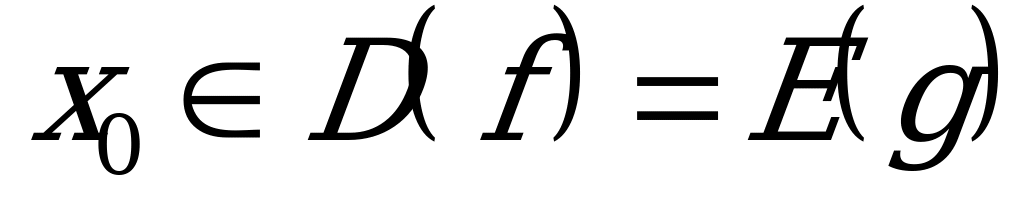 и
и 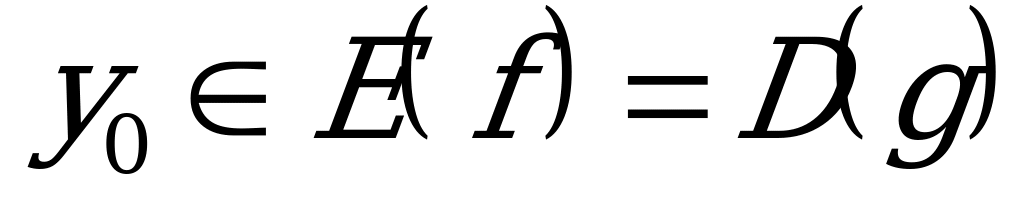 имеет место
имеет место 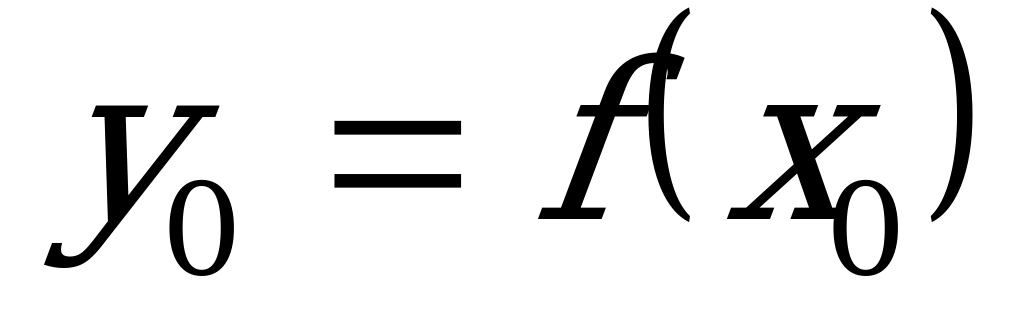 тогда и только тогда, когда
тогда и только тогда, когда 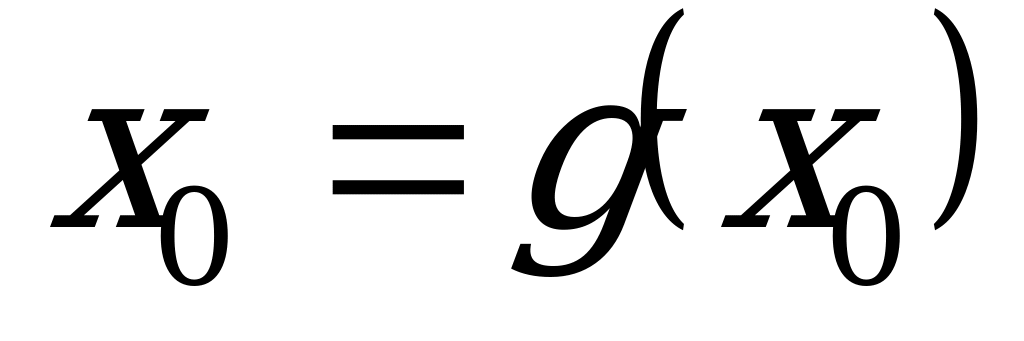 .
.
Из определения следуют тождества: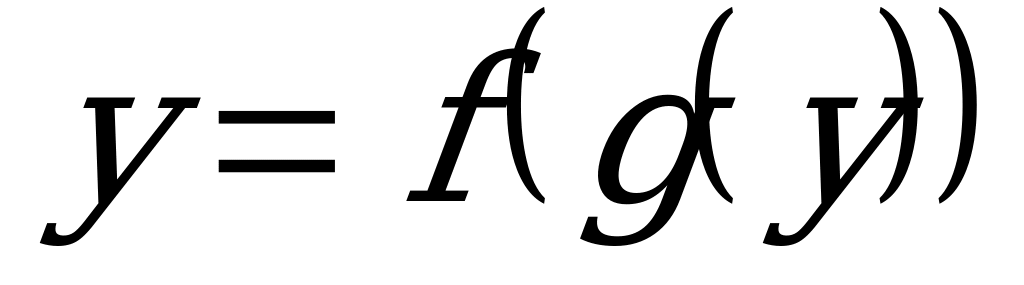 /1/
/1/
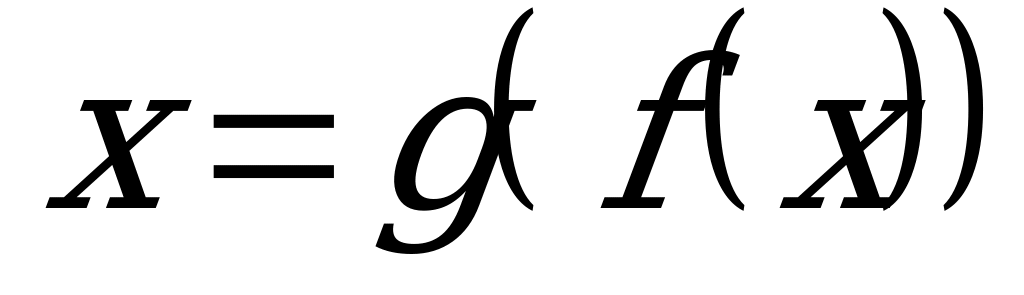 /2/
/2/
Если аргумент обозначить, как обычно, символом х, а функцию – через y, то для обратной функции получим формулу 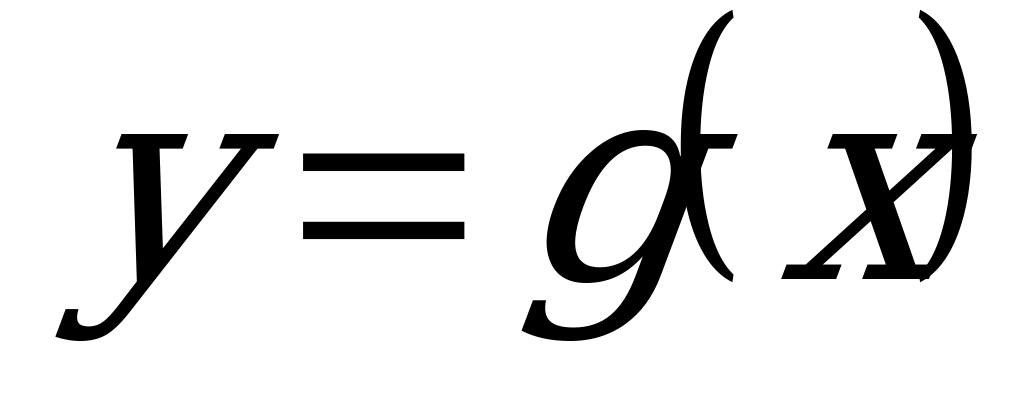 ./3/
./3/
Заметим, что обратную функцию можно получить из прямой функции 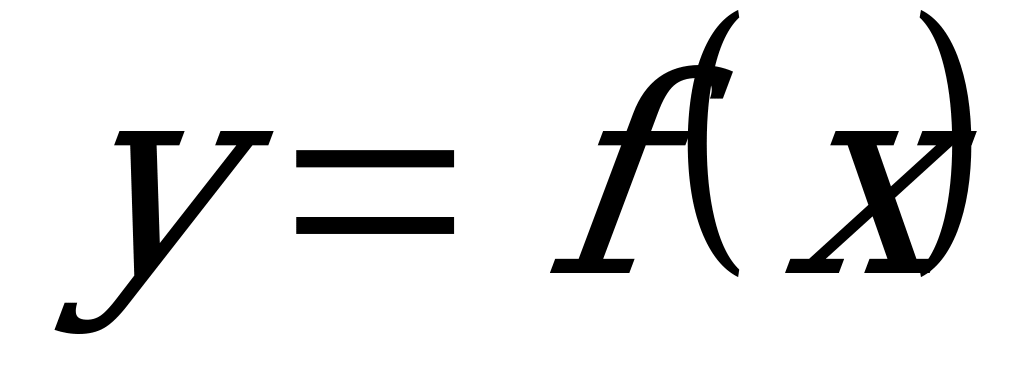 , меняя ролями аргумент x и функцию y, т.е. заменяя x на y и y на x.
, меняя ролями аргумент x и функцию y, т.е. заменяя x на y и y на x.
Таким образом, обратная функция к функции 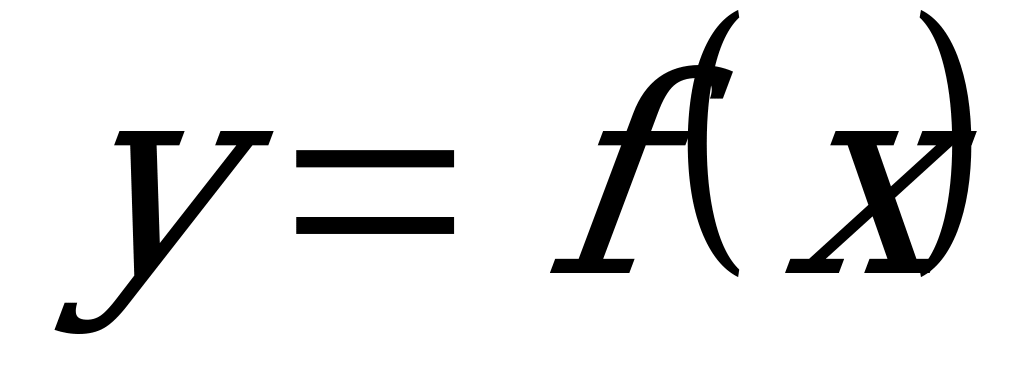 в неявной форме задается уравнением:
в неявной форме задается уравнением: 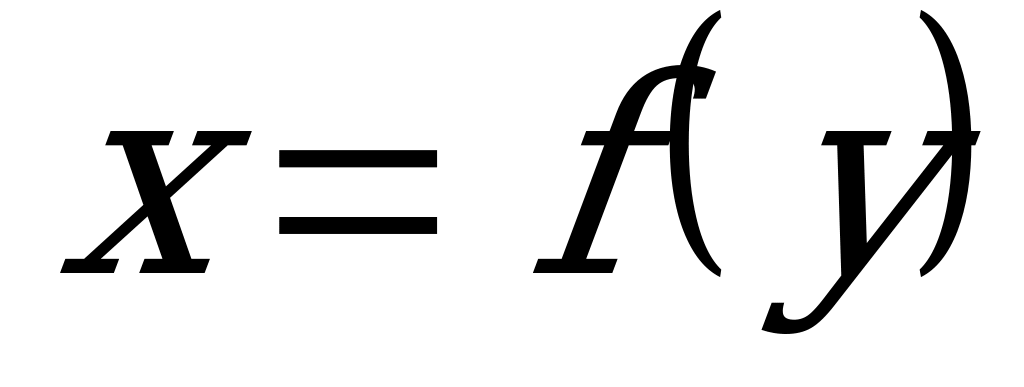 /4/.
/4/.
Если из /4/ выразить y через x, то получится явная форма /3/.
Обратная функция к функции f часто обозначается символом 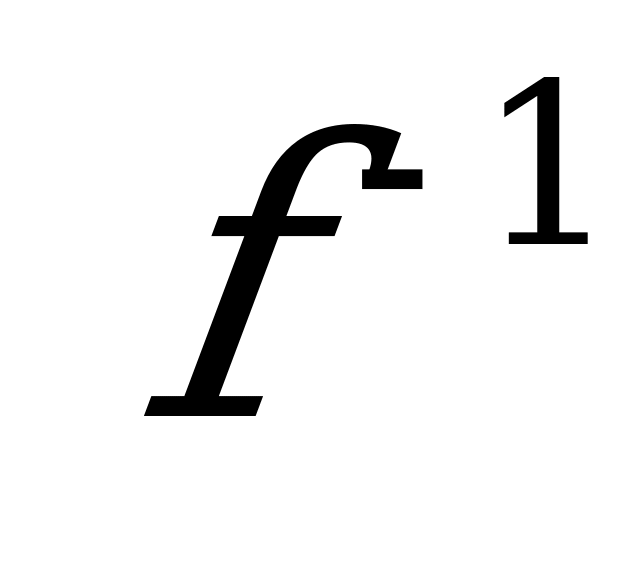 в отдельных случаях вводятся и другие обозначения. Легко видеть, что обратной к функции
в отдельных случаях вводятся и другие обозначения. Легко видеть, что обратной к функции 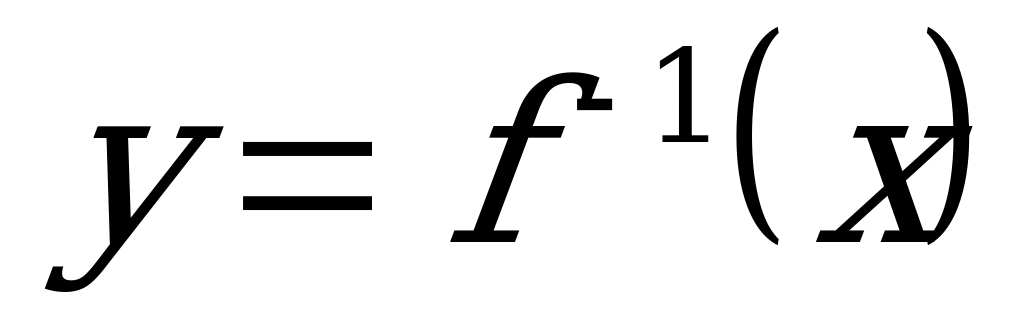 будет функция
будет функция 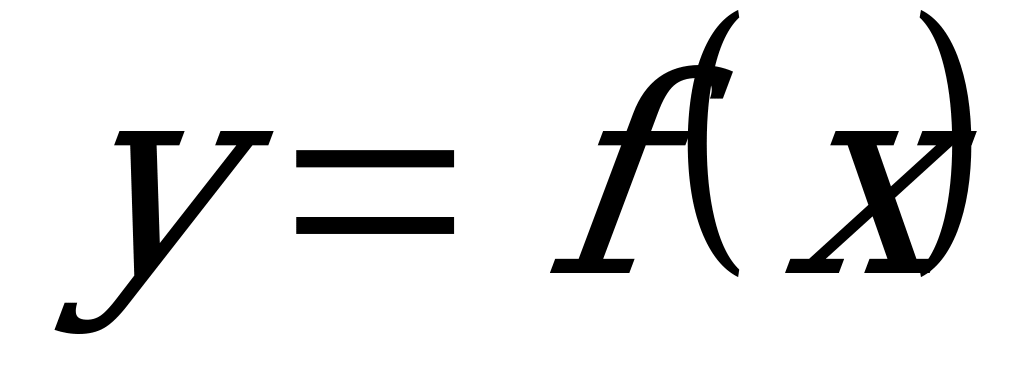 , т.е.
, т.е. 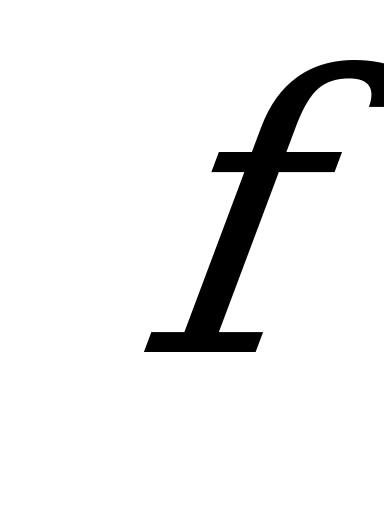 и
и 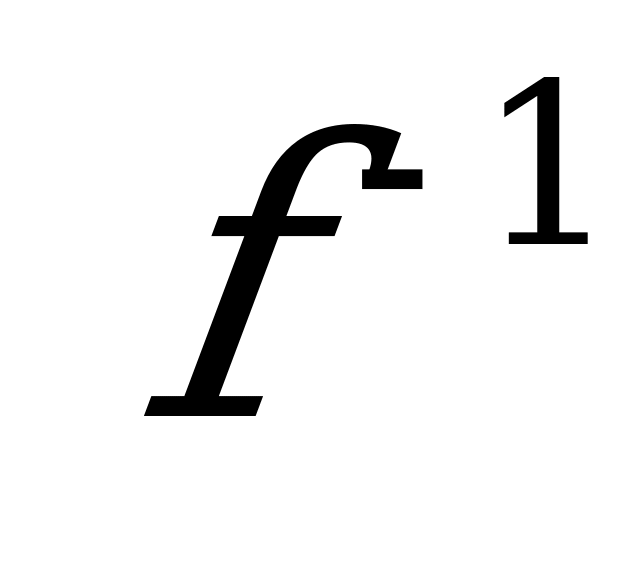 -взаимно обратные функции.
-взаимно обратные функции.
Функция 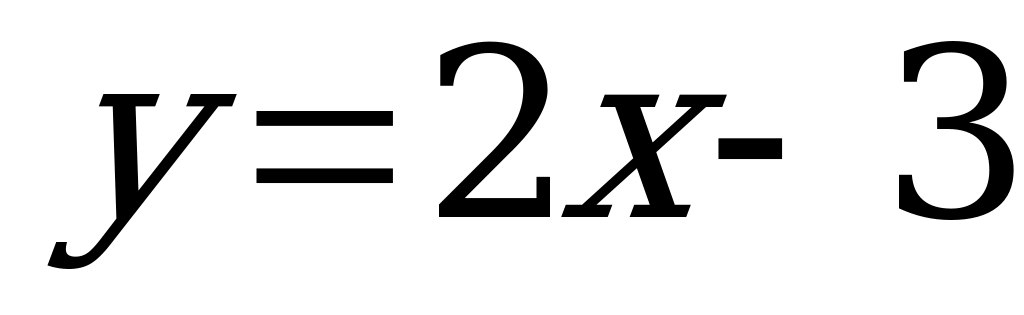 имеет обратную функцию
имеет обратную функцию 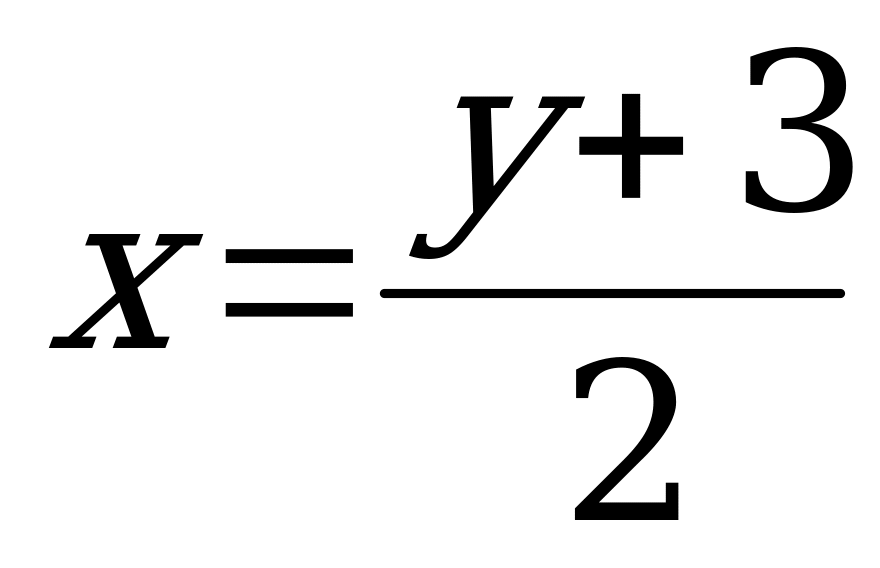 или, переходя к обычным обозначениям для аргумента и функции, получим:
или, переходя к обычным обозначениям для аргумента и функции, получим: 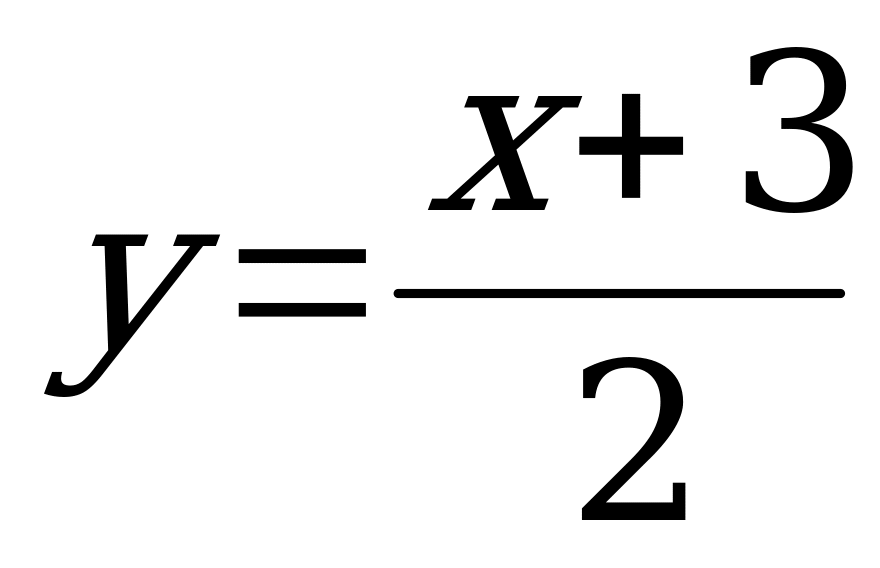 .
.
Определение: Графиком функции 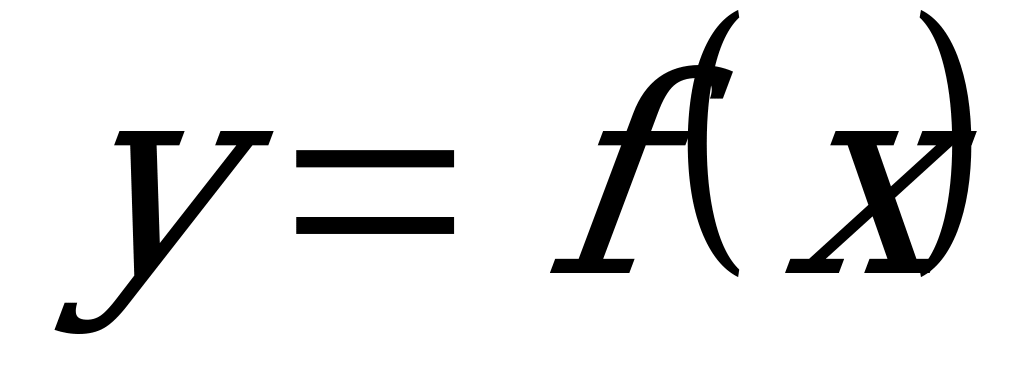 называется множество всех точек координатной плоскости с координатами
называется множество всех точек координатной плоскости с координатами 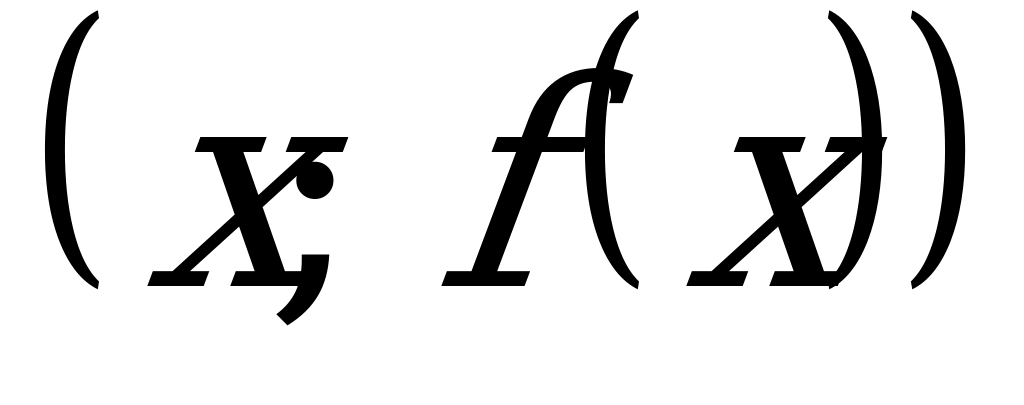 .
.
Рассмотрим основные элементарные функции и их графики.
| № | Вид функции | Название функции | 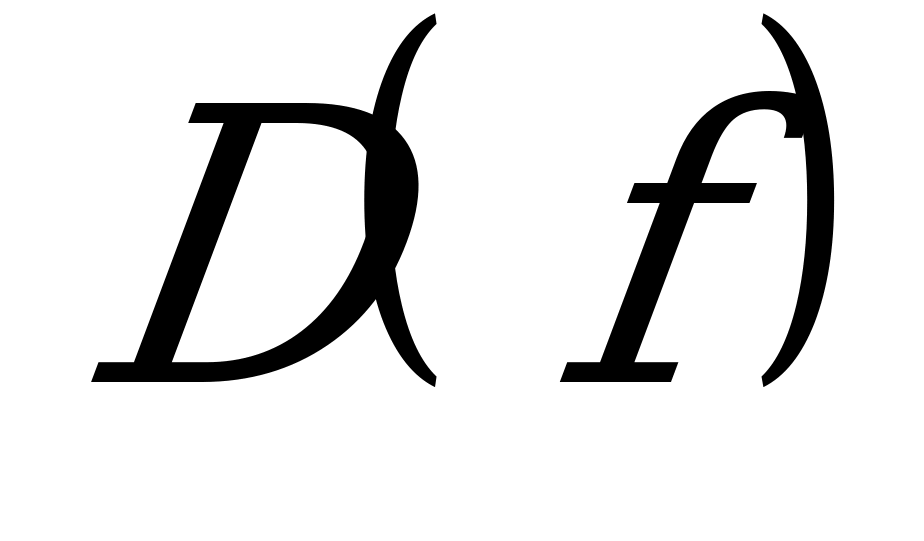
| 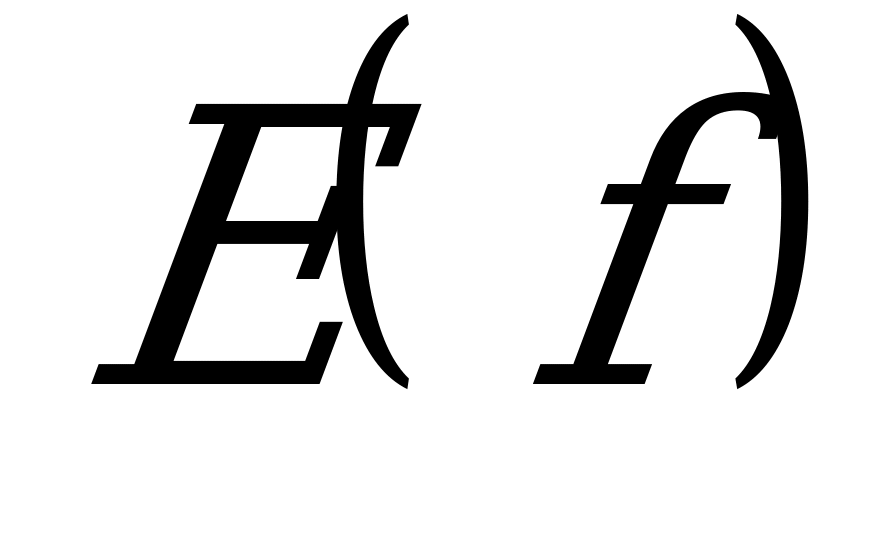
| Название графика | Вид графика |
| 1 | 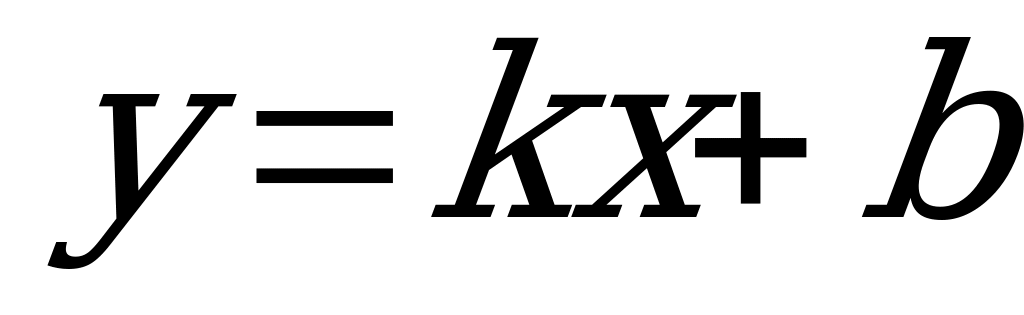 k0, I-III четверти kII-IV | линейная | R | R | прямая | 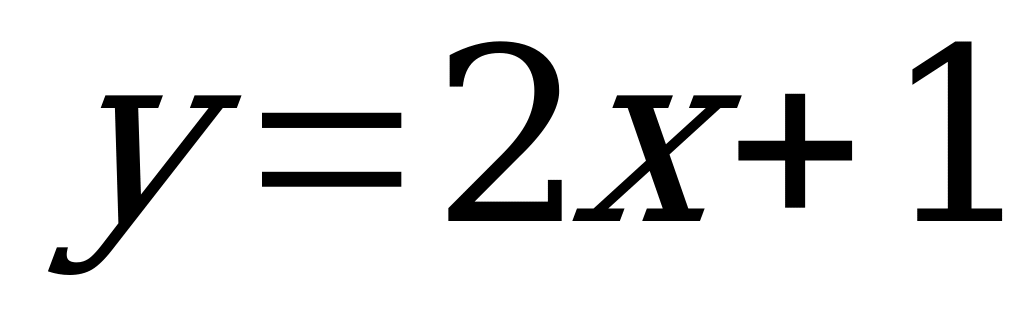 | 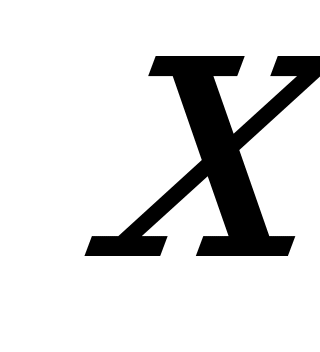
| 0 | 2 | | 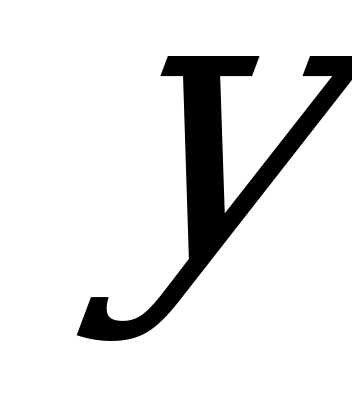
| 1 | 5 |
|
| 2 | 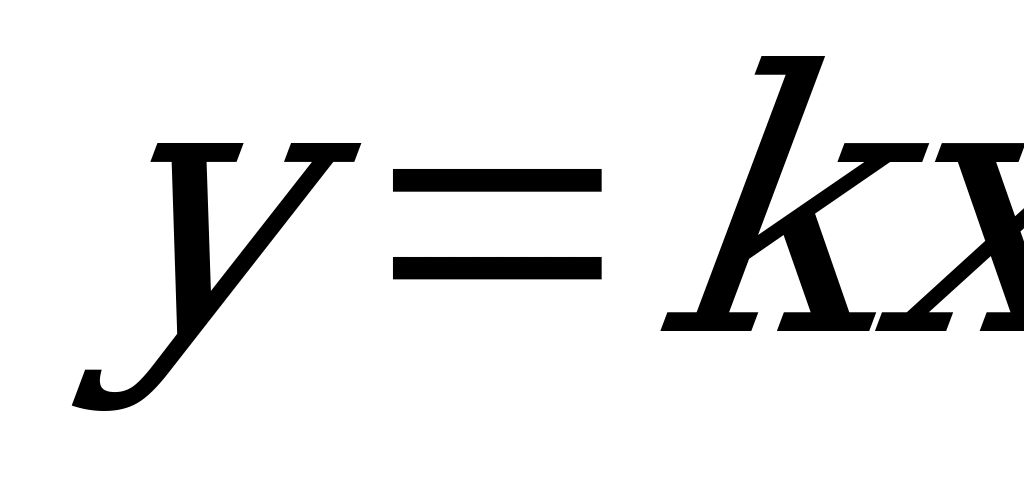 k0, I-III четверти kII-IV | Прямая пропорциональность | R | R | Прямая, проходящая Через О(0;0) | 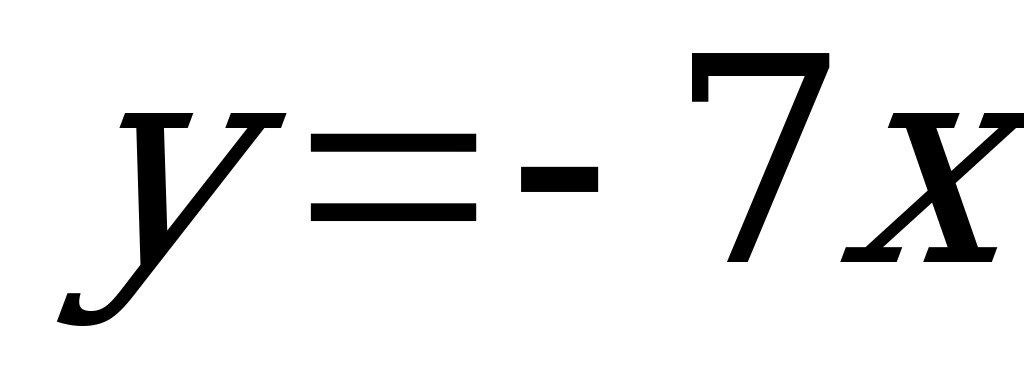 | 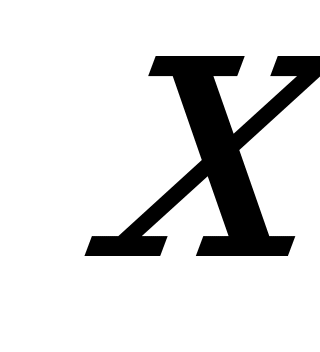
| 0 | 1 | | 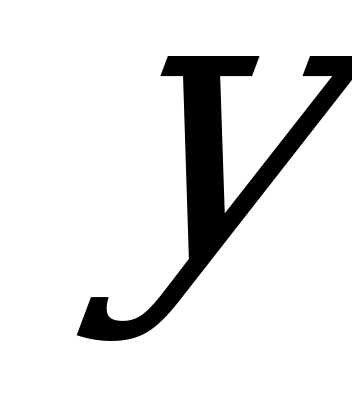
| 0 | -7 |
|
| 3. | 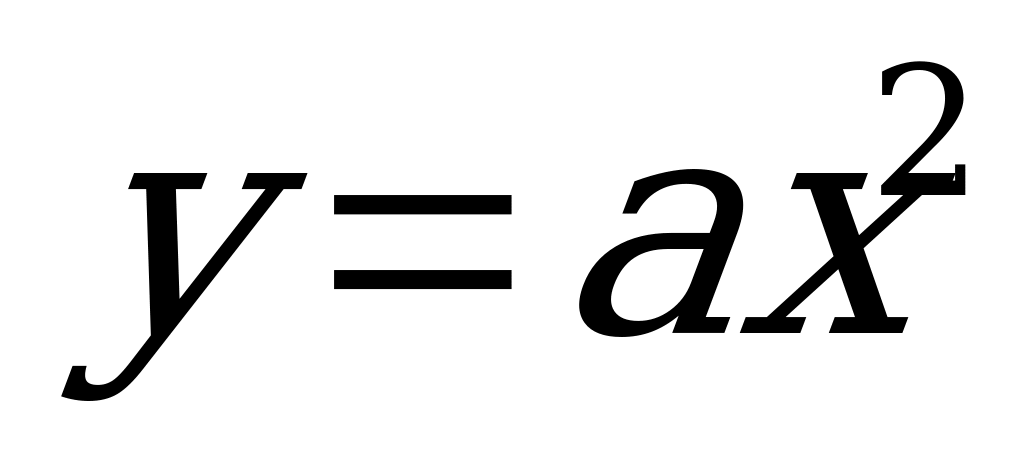 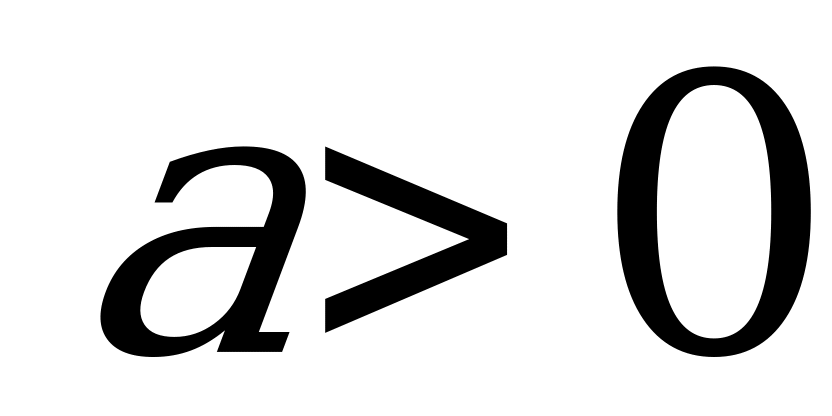 -ветви вверх -ветви вверх 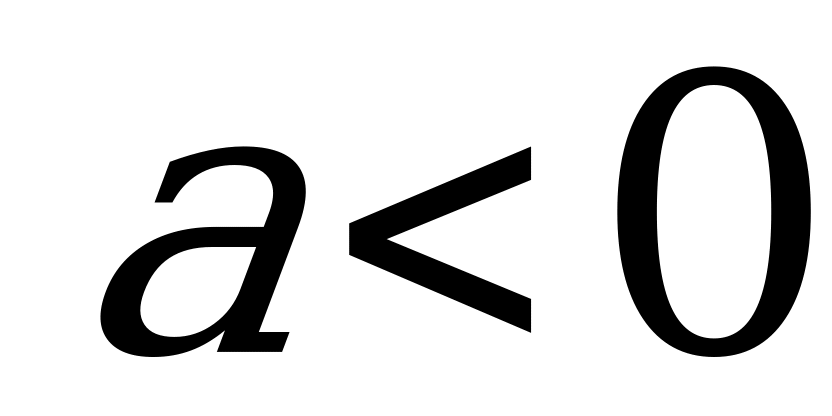 - ветви вниз - ветви вниз
| Квадратичная функция | R | R | парабола | 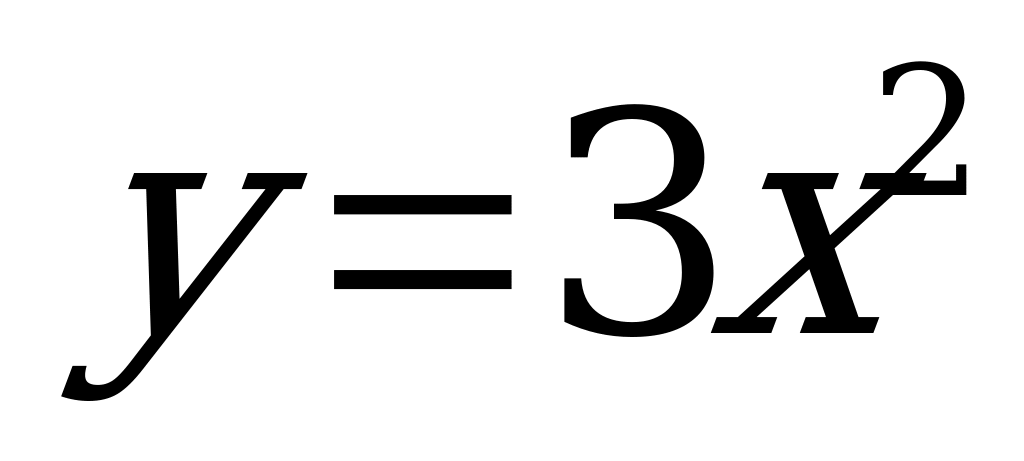   |
| 4. | 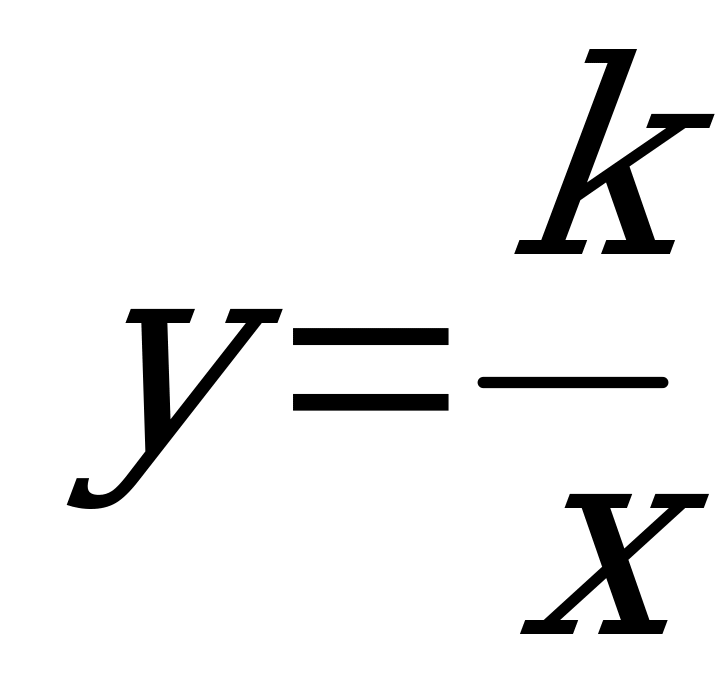 k0, I-III четверти kII-IV | Обратная пропорциональность | 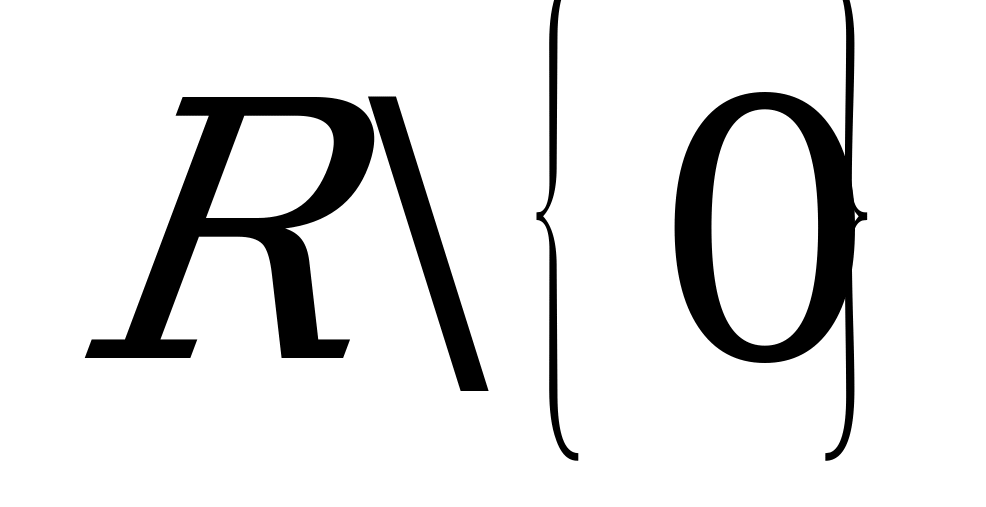 | 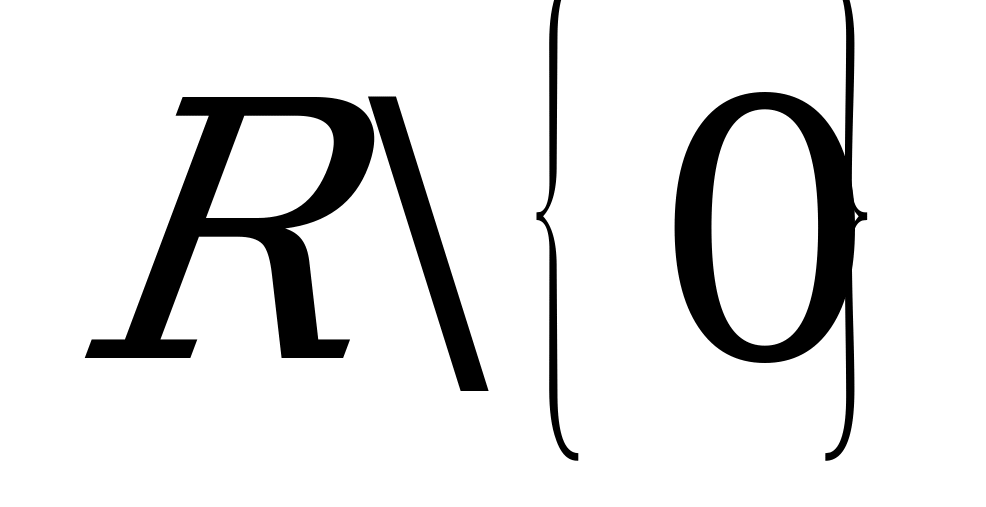 | гипербола | 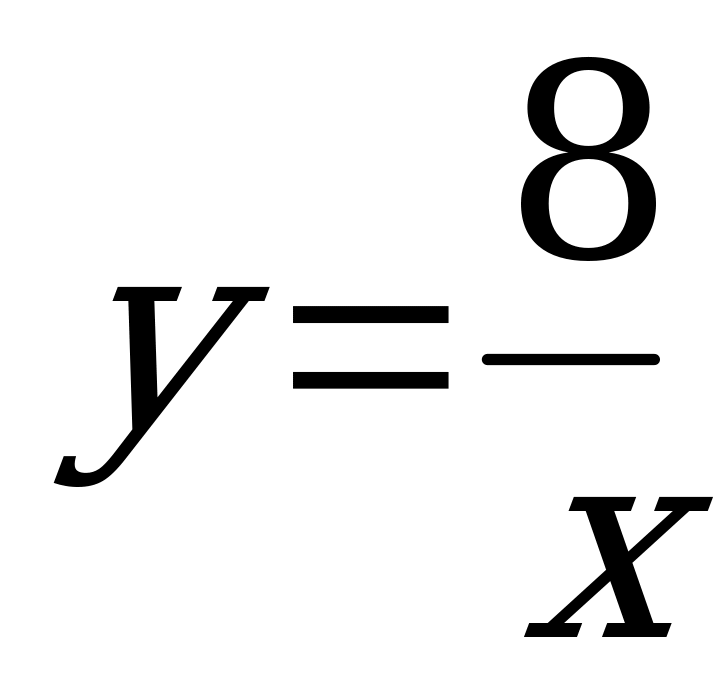 |
| 5. | 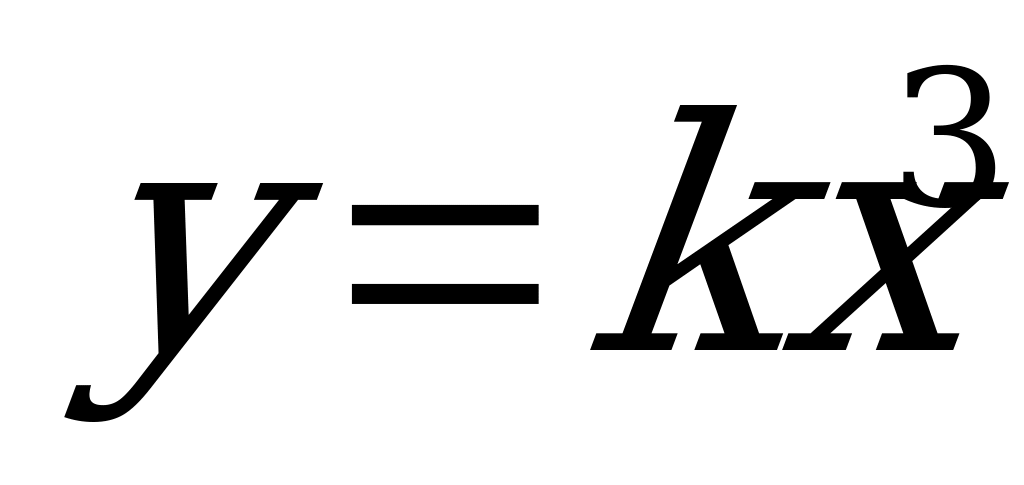 k0, I-III четверти kII-IV
| Кубическая | R | R | Кубическая парабола | 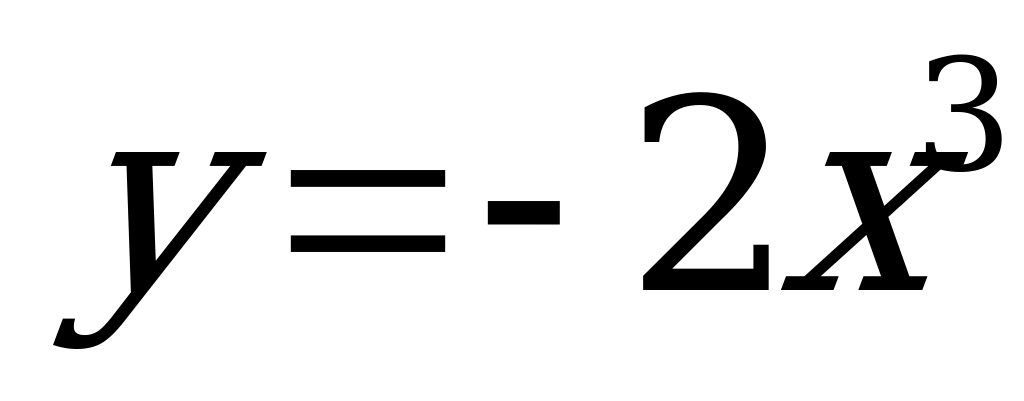 |
| 6. | 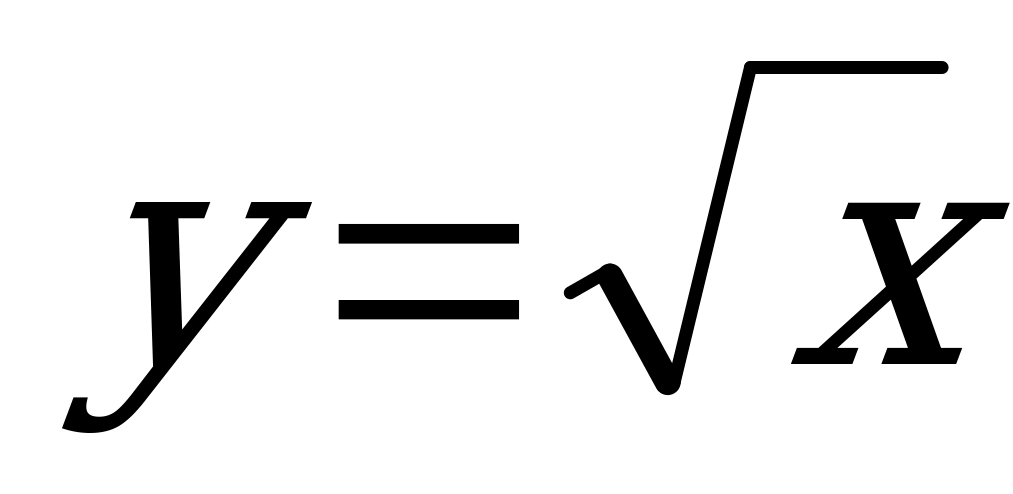 |
| 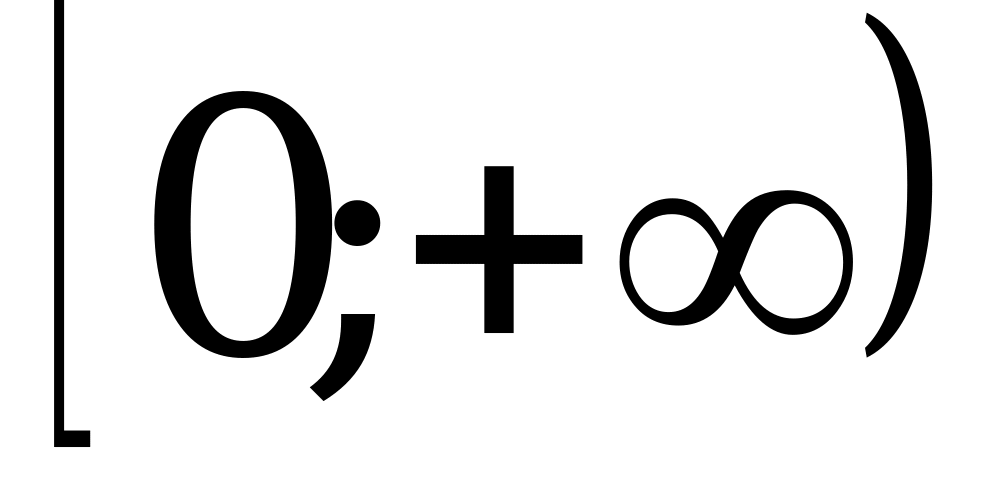 | 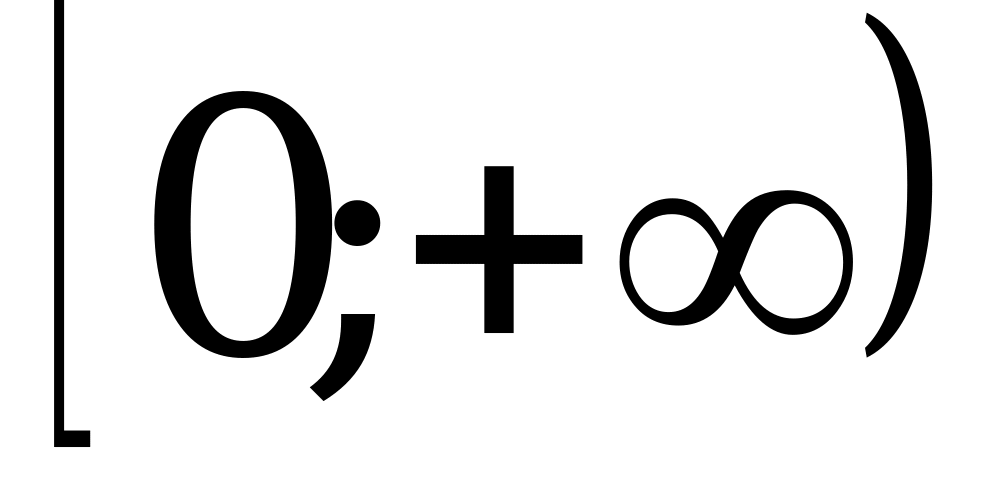 | Ветвь параболы Симметричной относительно оси ох |
|
Строить графики функций по точкам не всегда удобно. Чаще поступают более рационально: строят графики простейших функций, а графики более сложных функций получают из этих графиков путем некоторых преобразований.
Итак, запишите в Ваши конспекты наши выводы:
y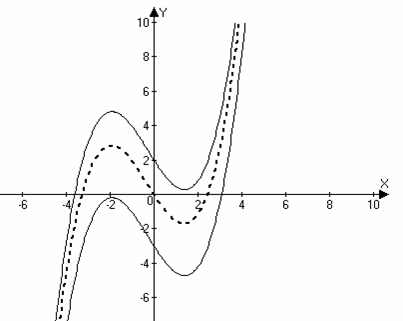
= f(x) + b – график функции получается из графика функции y = f(x) путем параллельного переноса этого графика на величину вдоль от ОУ. при этом, если b0, то график функции f(x) + b располагается выше графика функции f(x), если b
y = f (x + b) – график функции получается из графика функции y = f(x) с помощью параллельного переноса этого графика на величину b вдоль оси ОХ, при этом, если b0, то сдвиг влево, а если b
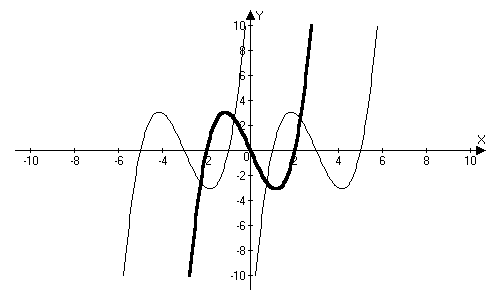
y = - f(x) – график симметричен графику y = f(x) относительно оси ОХ
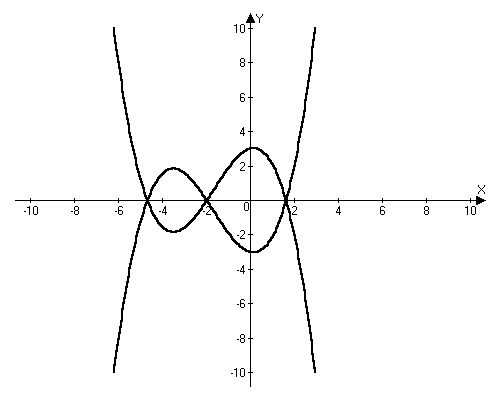
Указанные преобразования не изменяют масштаба графика функции.
Рассмотрим преобразования графиков функций, которые изменяют масштаб графика
y = аf(x) – график функции получается из графика функции y = f(x) с помощью растяжения или сжатия графика по оси ОУ пропорционально коэффициенту а, причем,
если a 1, то все ординаты графика аf(x) увеличиваются в а раз, если a а раз.
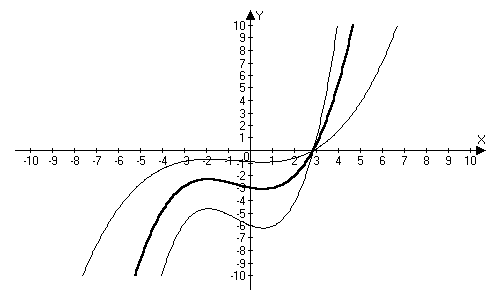
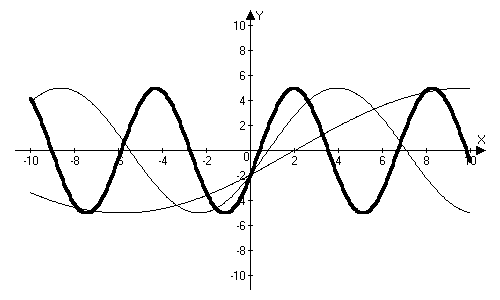
y = f(аx) – график функции получается из графика функции y = f(x) с помощью растяжения или сжатия вдоль оси ОХ пропорционально коэффициенту а, причем, если, а 1, то график сжимается в а раз, если 0 a а раз.
у = 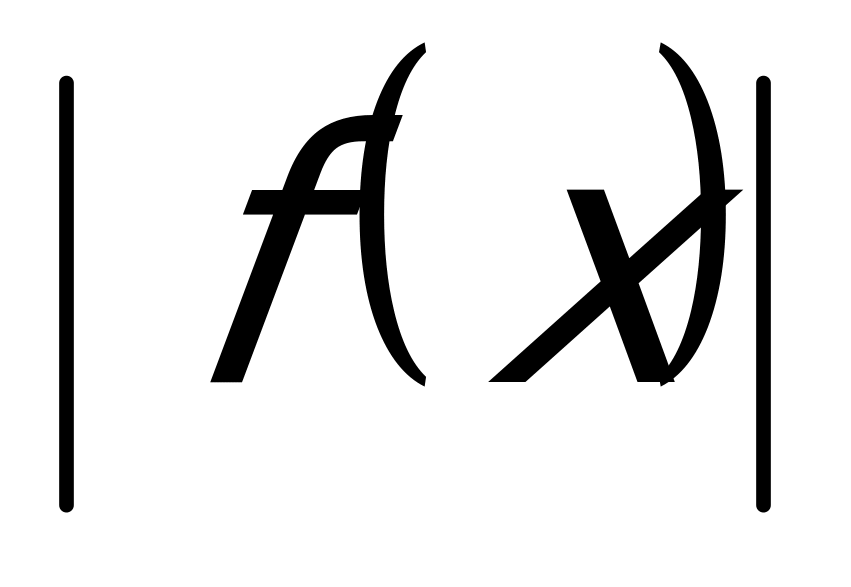 - для построения этого графика нужно построить график функции y = f(x) и отобразить относительно оси ОХ те части графика, которые расположены ниже этой оси.
- для построения этого графика нужно построить график функции y = f(x) и отобразить относительно оси ОХ те части графика, которые расположены ниже этой оси.
у = 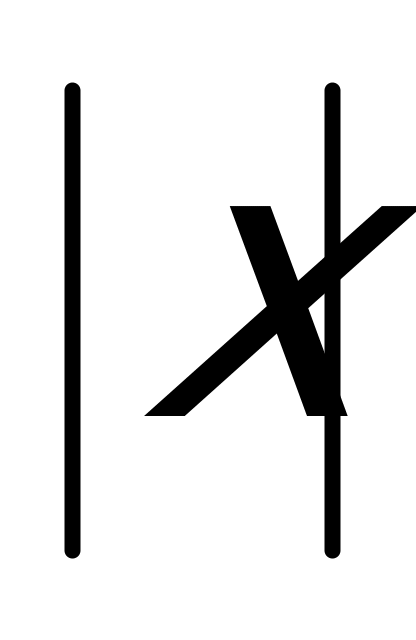 у = х – 3; у =
у = х – 3; у = 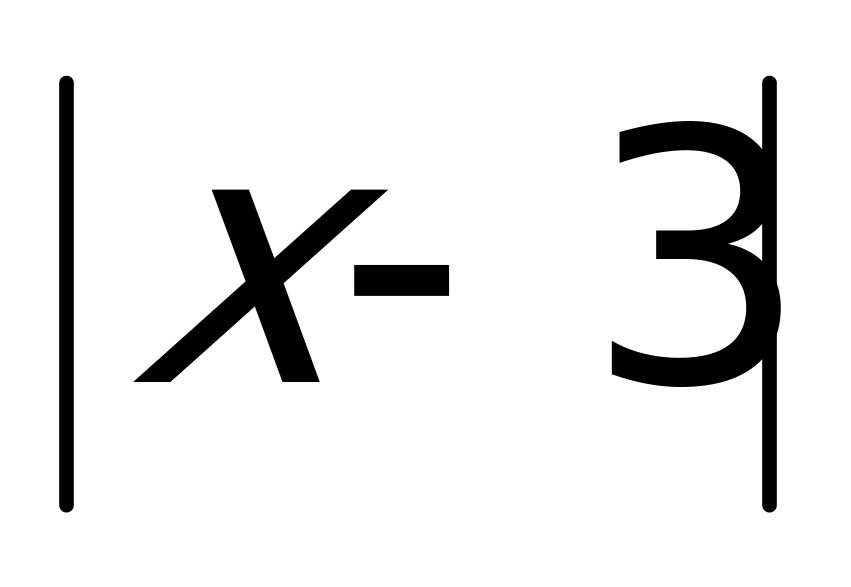
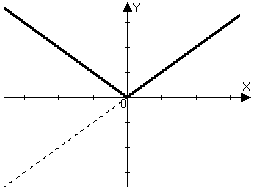
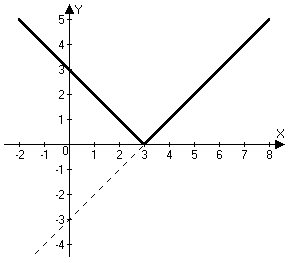
у = 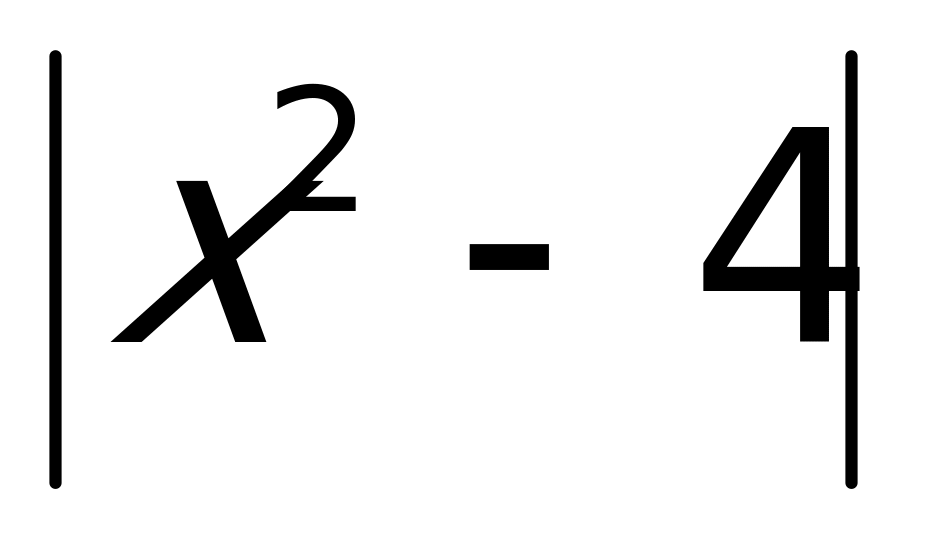 у = х2 – 4
у = х2 – 4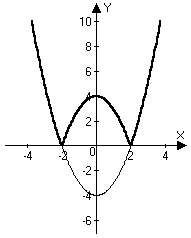
Вариант 1
№ 1. Дан график некоторой функции 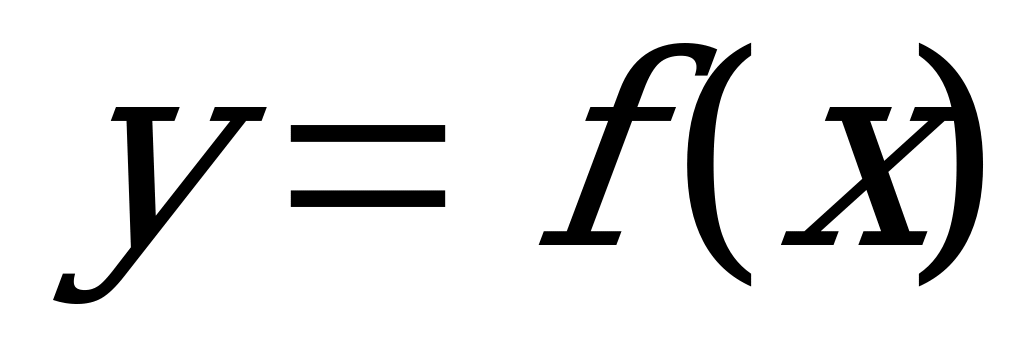
| 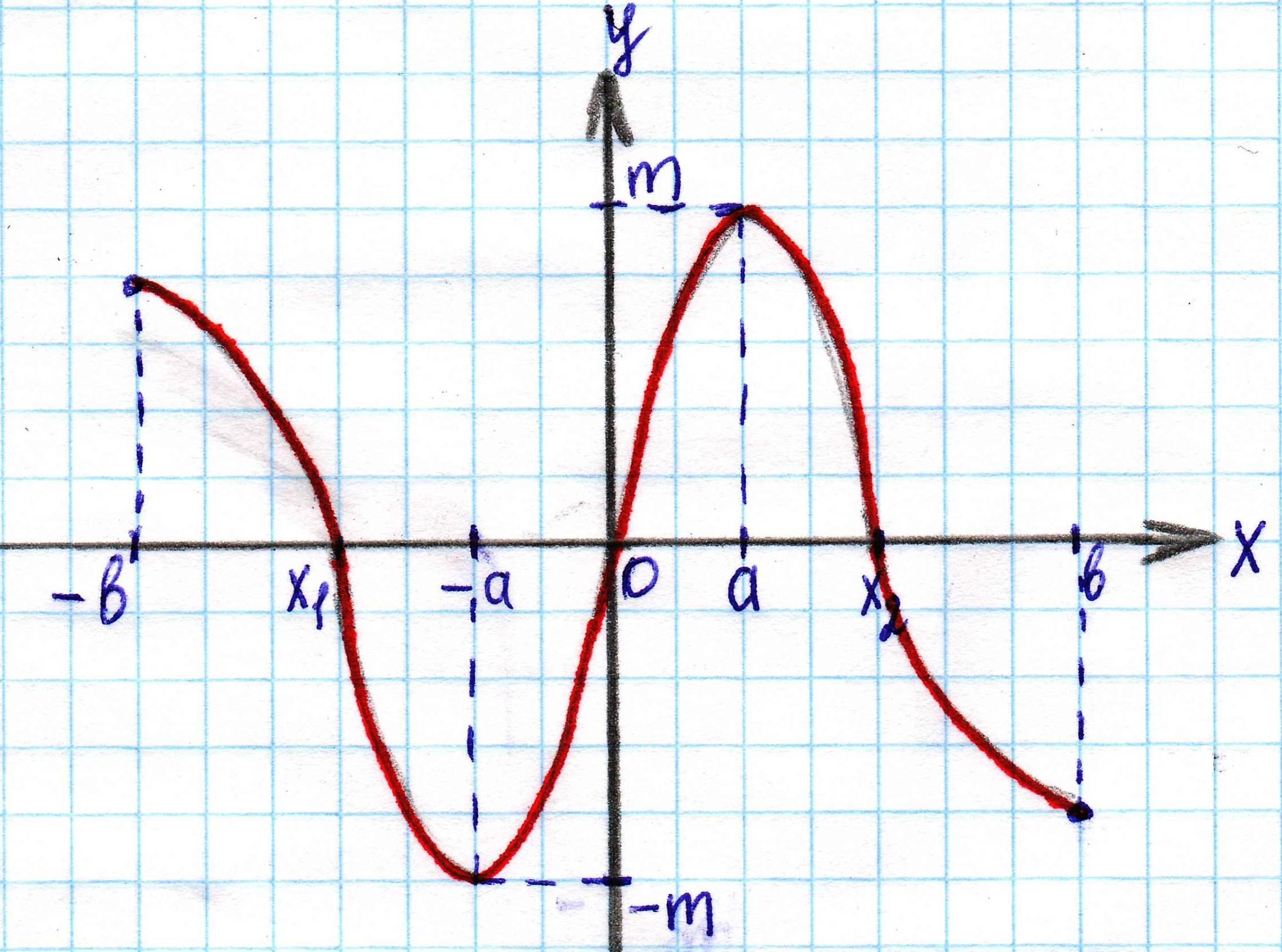
| Запишите: а) D(y), E(y); б) промежутки возрастания, убывания; в) промежутки где 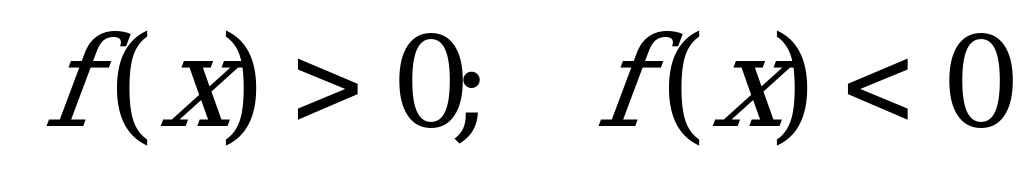 ; ; г) точки, в которых f(x) = 0; д) укажите является ли данная функция четной, нечетной или общего вида.
|
№ 2. Найдите значение функции в точке:
А)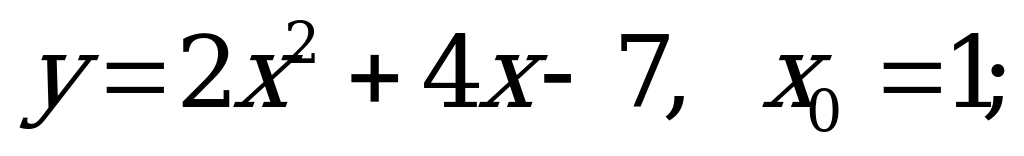 б)
б)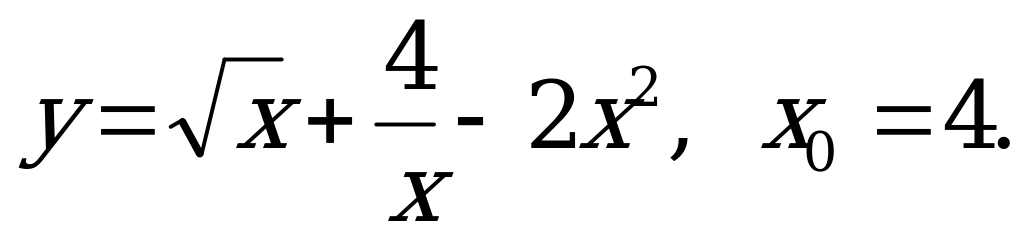
№ 3. Найдите область определения функций:
А)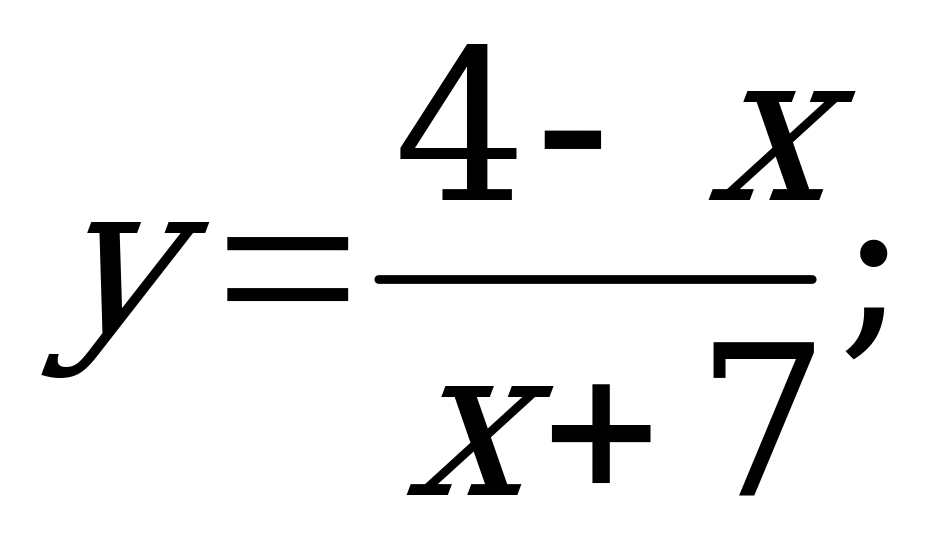 б)
б)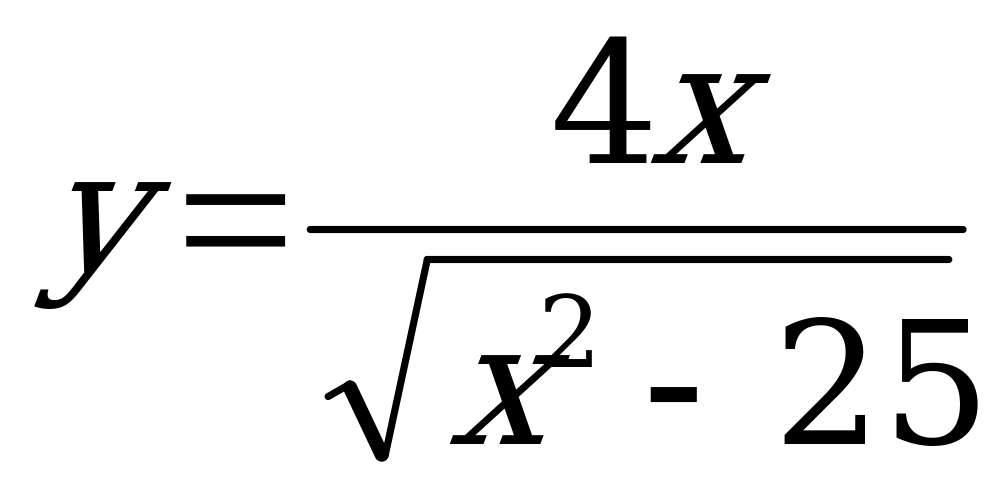
№ 4. Найдите обратную функцию:
А) 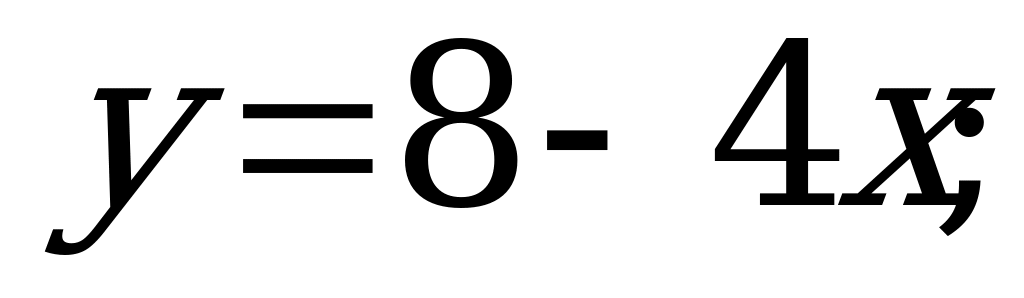 б)
б) 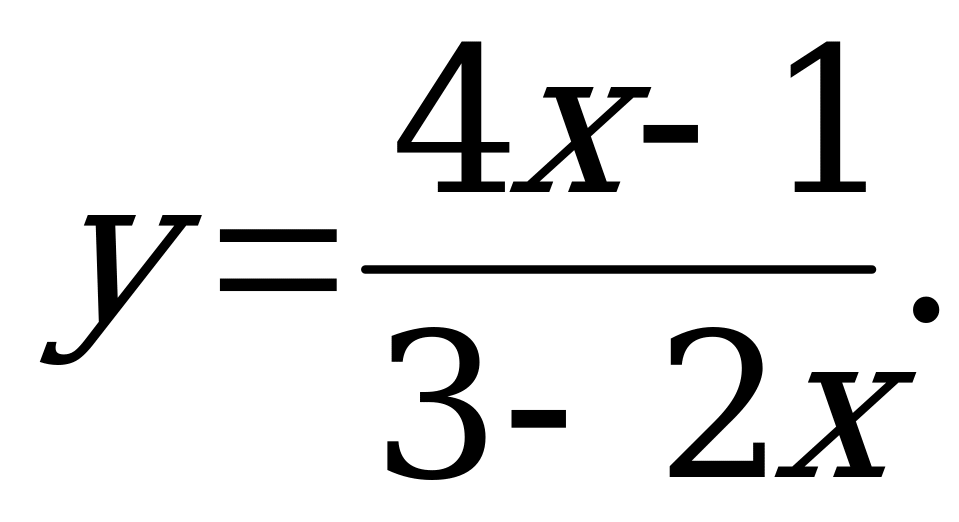
№ 5. Выполните действия над функциями: 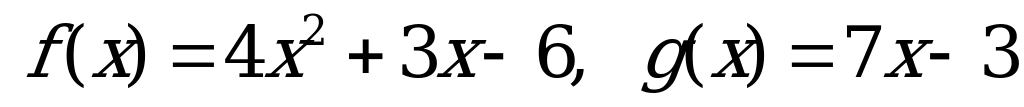
А)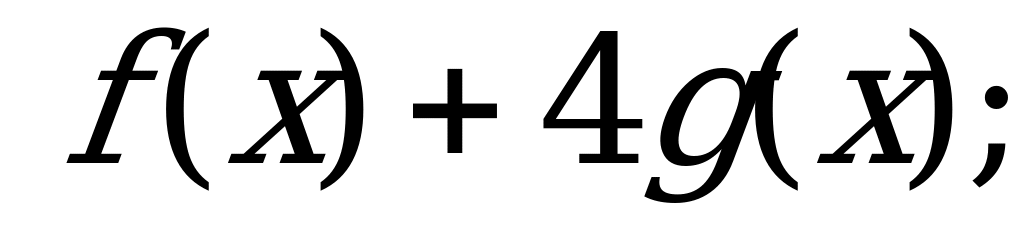 б)
б) 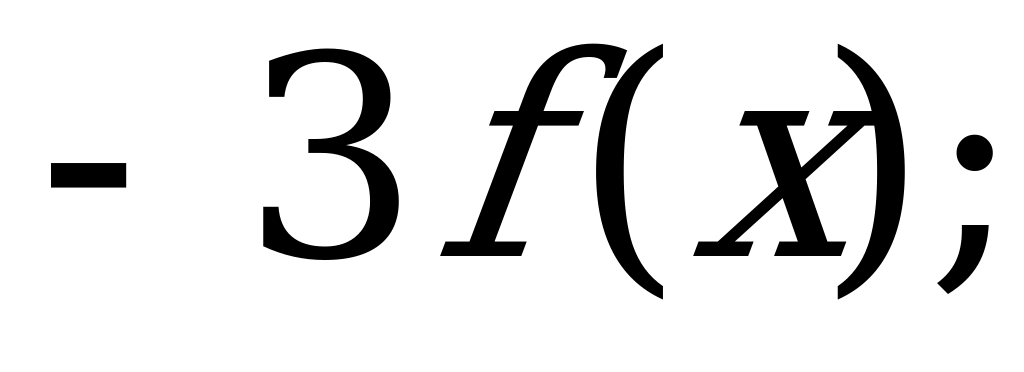 в)
в) 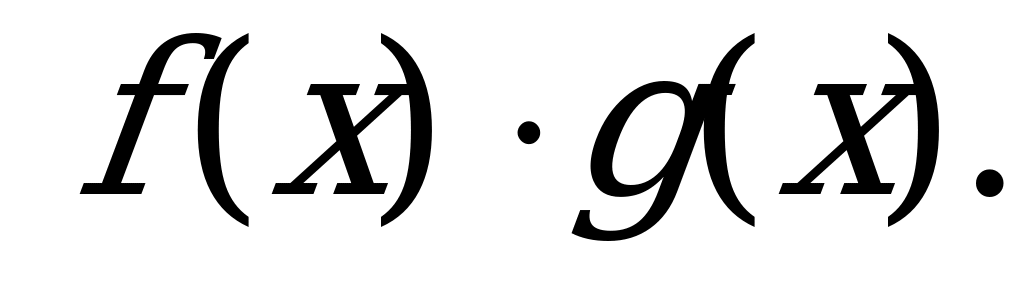
№ 6. Найдите координаты точки пересечения графиков функций: 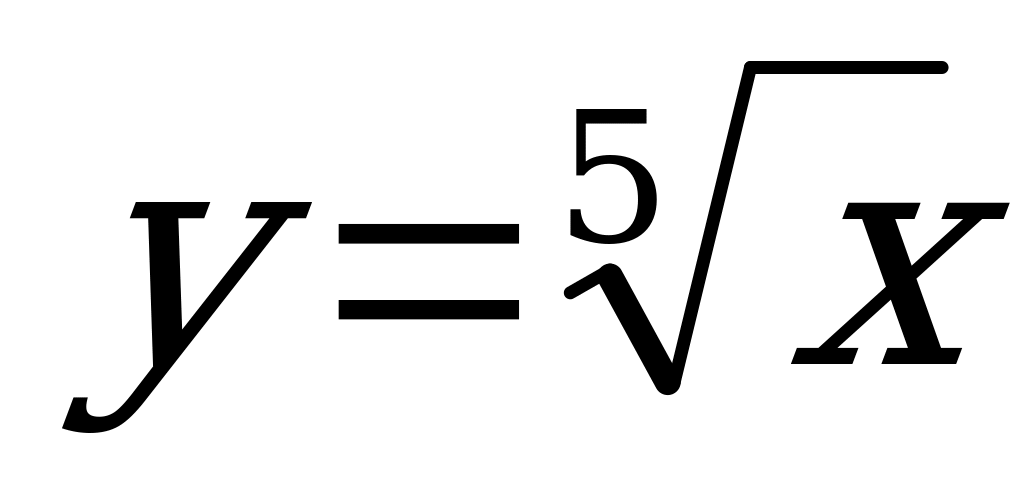 и
и 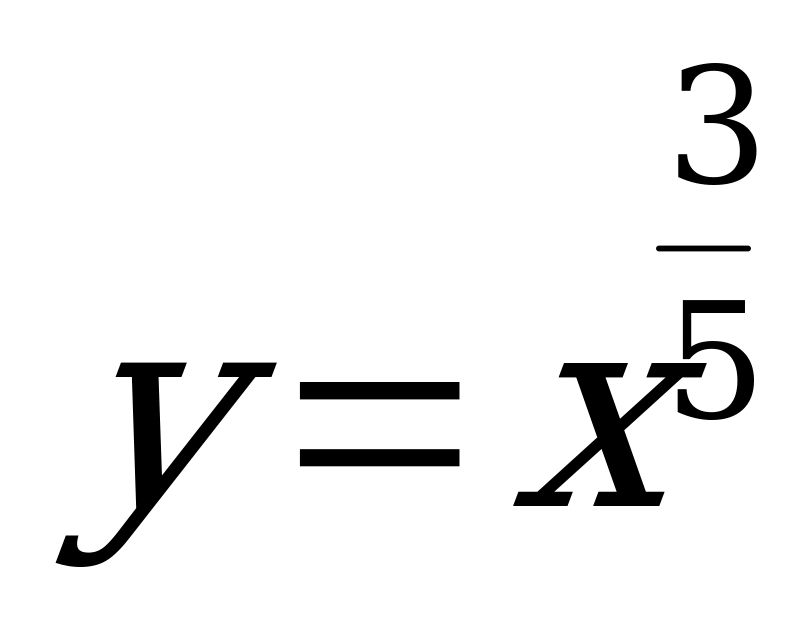
№ 7 Функция f(x) убывающая, сравните:
А)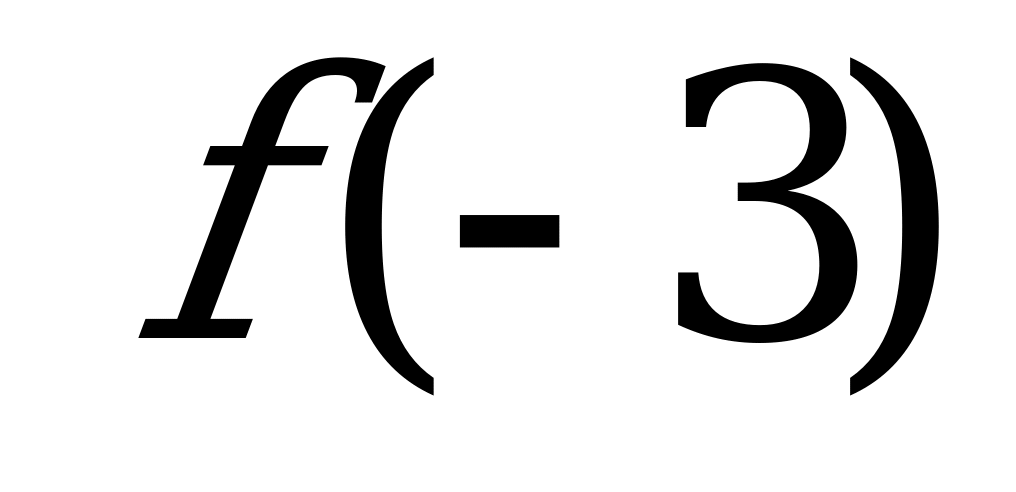 и
и 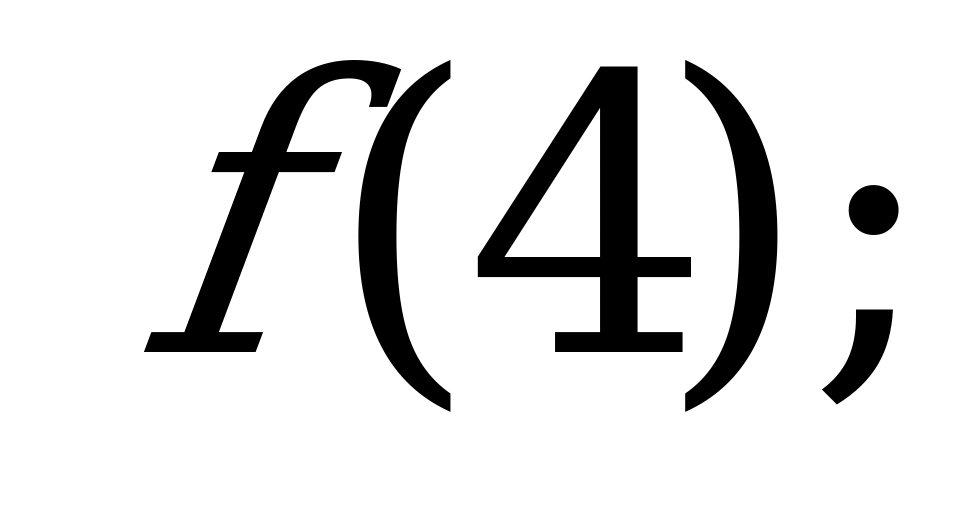 б)
б) 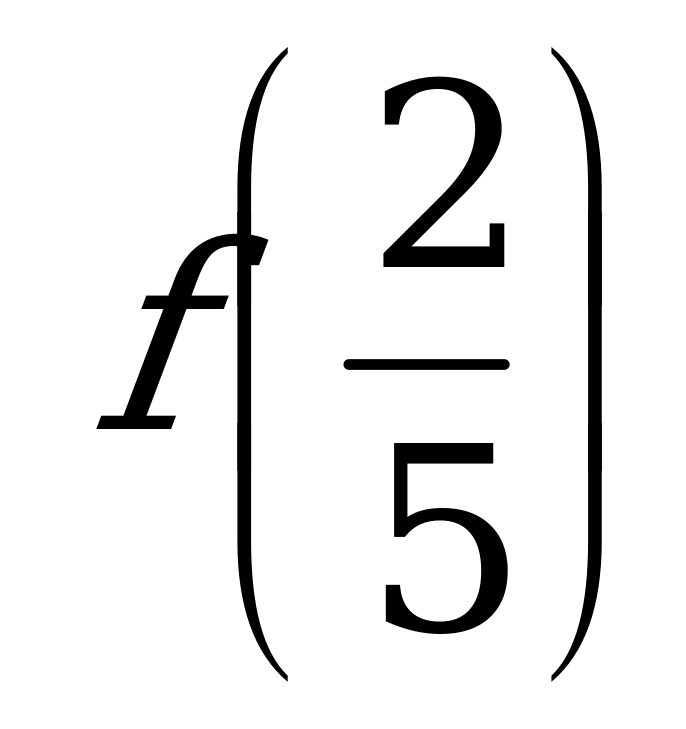 и
и 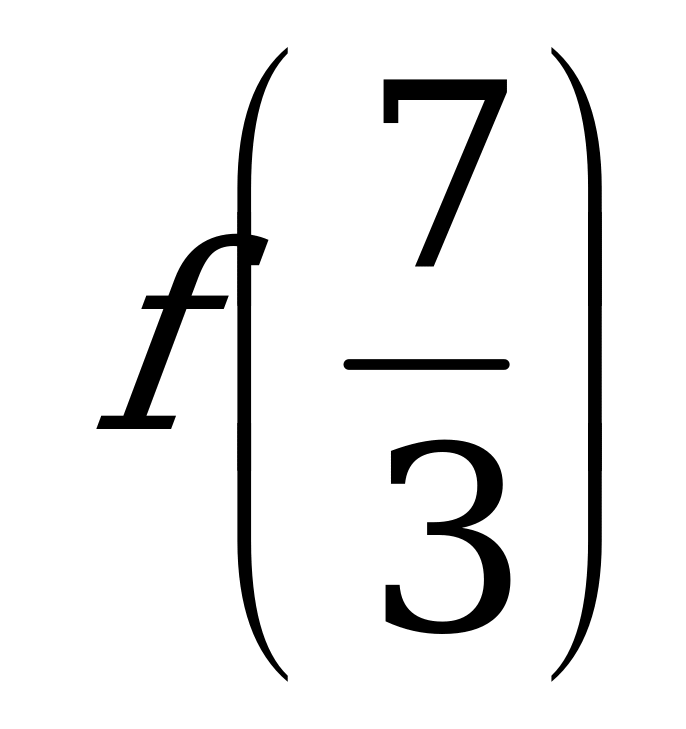
№ 8 Построить график функции с помощью элементарных преобразований:
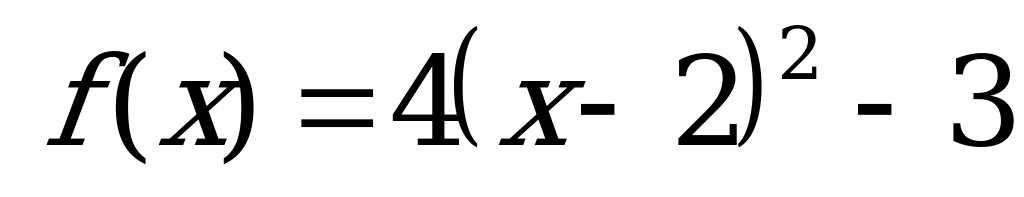
Вариант 2
№ 1. Дан график некоторой функции 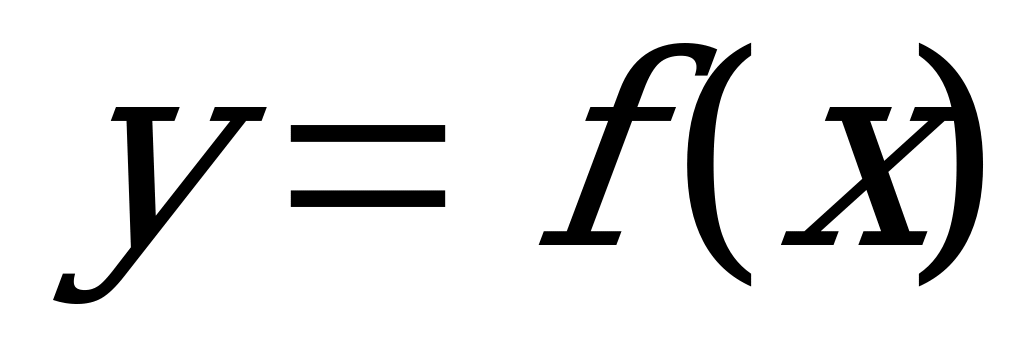
| 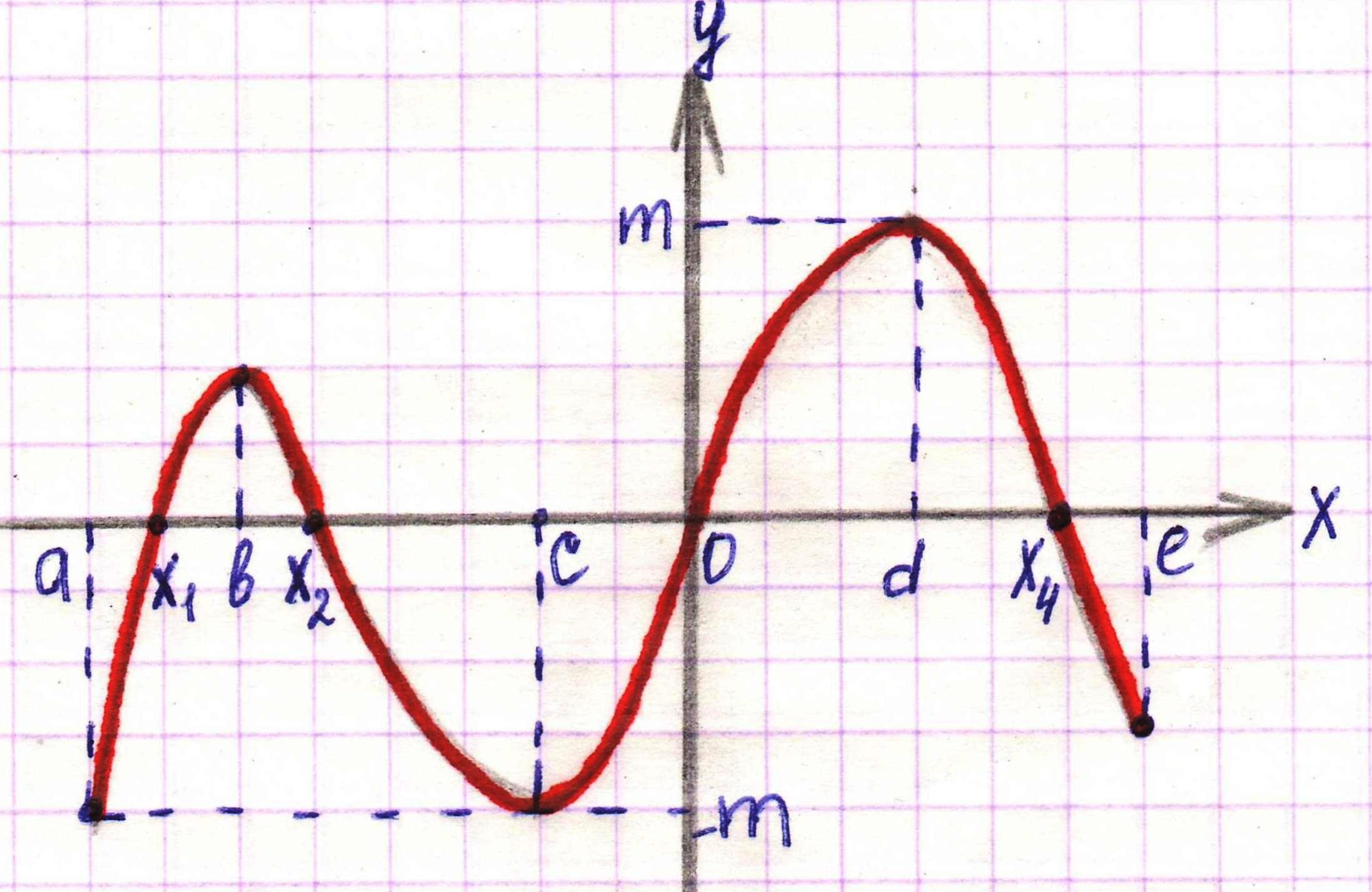
| Запишите: а) D(y), E(y); б) промежутки возрастания, убывания; в) промежутки где 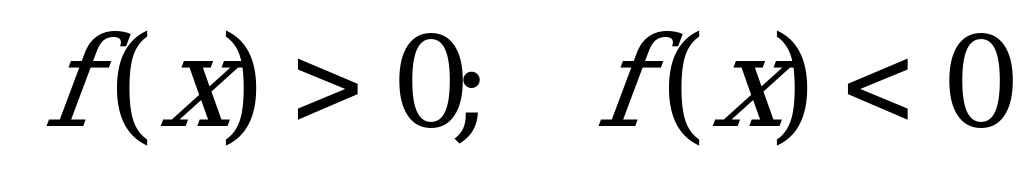 ; ; г) точки, в которых f(x) = 0; д) укажите является ли данная функция четной, нечетной или общего вида.
|
№ 2. Найдите значение функции в точке:
А) 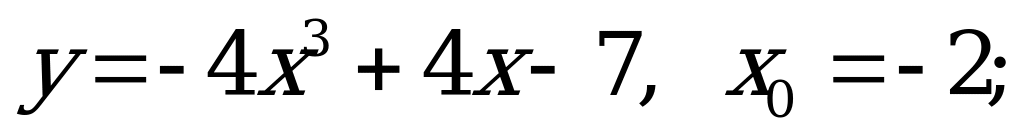 б)
б) 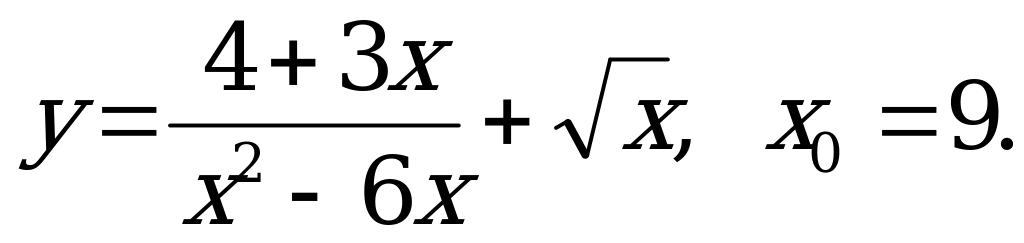
№ 3. Найдите область определения функций:
А) 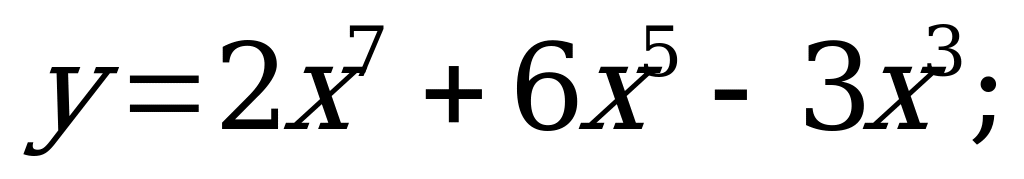 б)
б)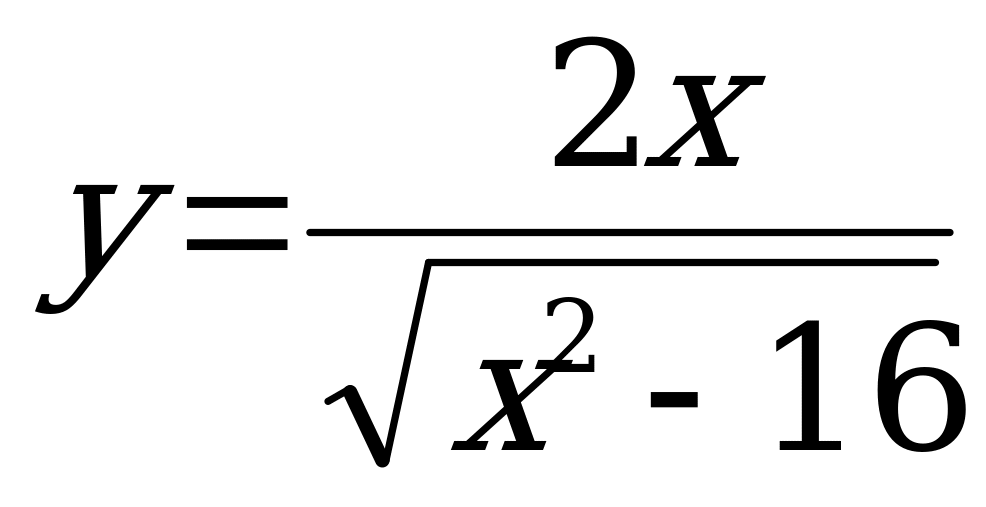
№ 4. Найдите обратную функцию:
А) 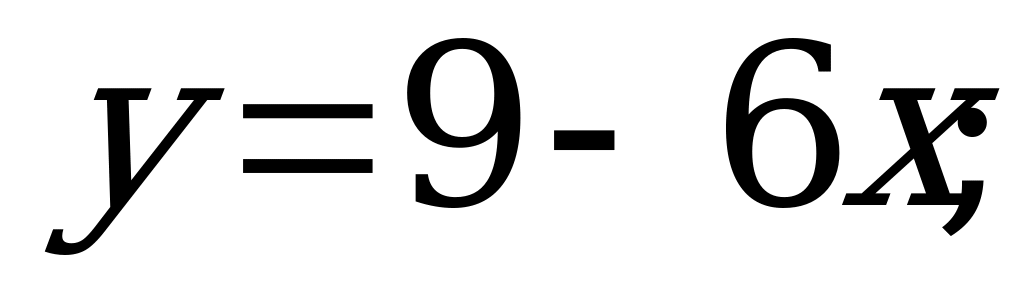 б)
б) 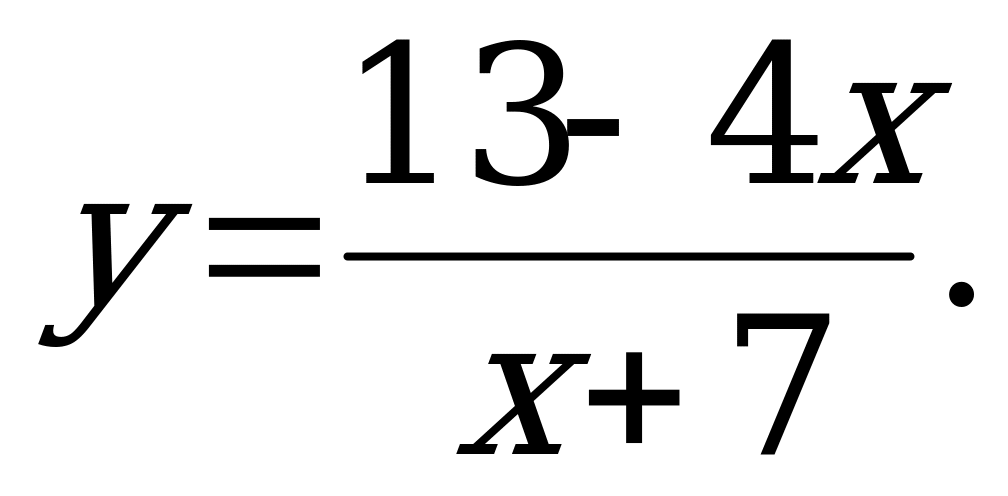
№ 5. Выполните действия над функциями: 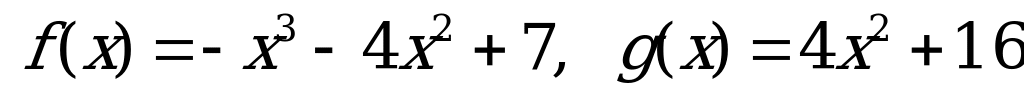
А) 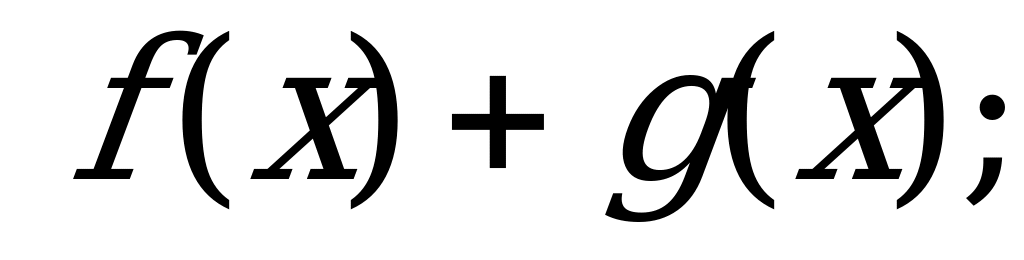 б)
б) 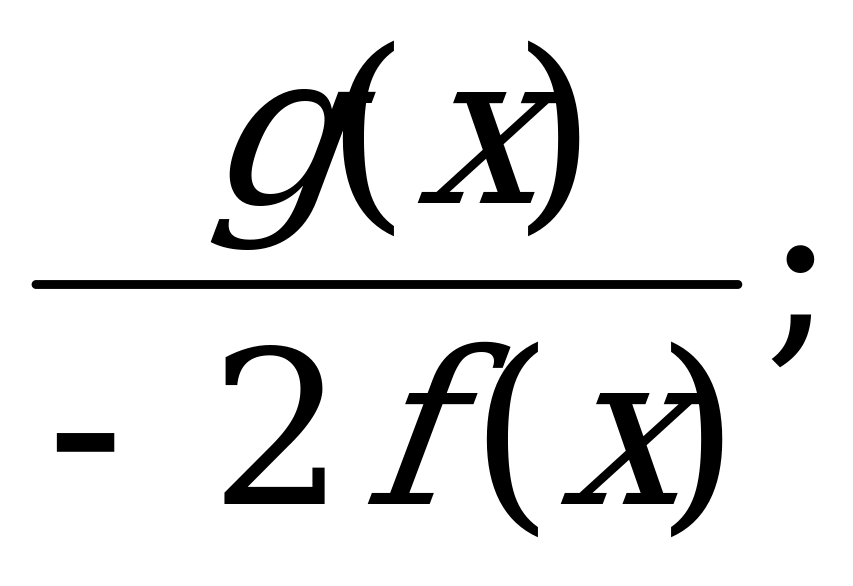 в)
в)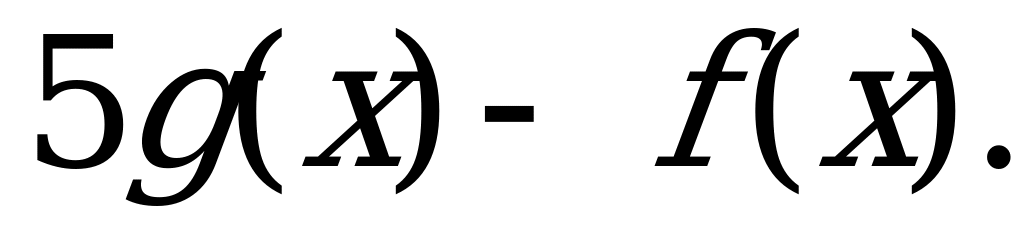
№ 6. При каких значениях параметра а областью значений функции 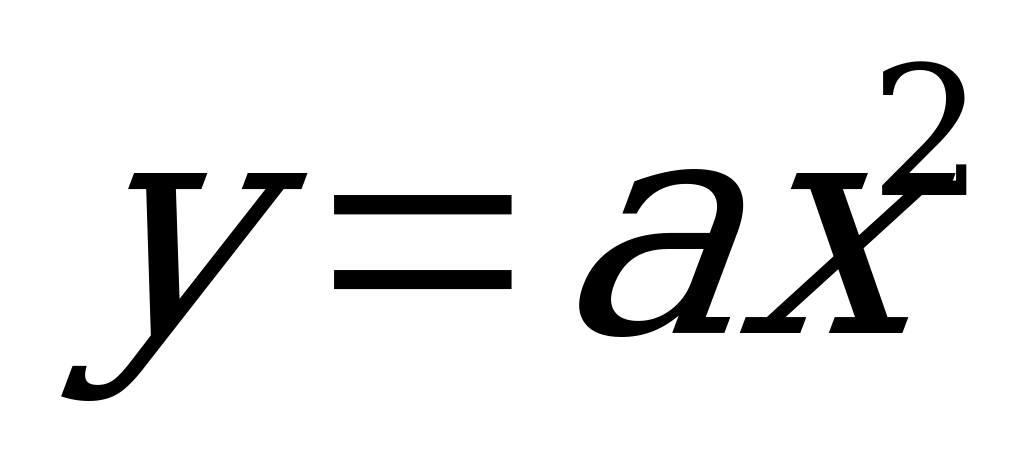 является промежуток
является промежуток 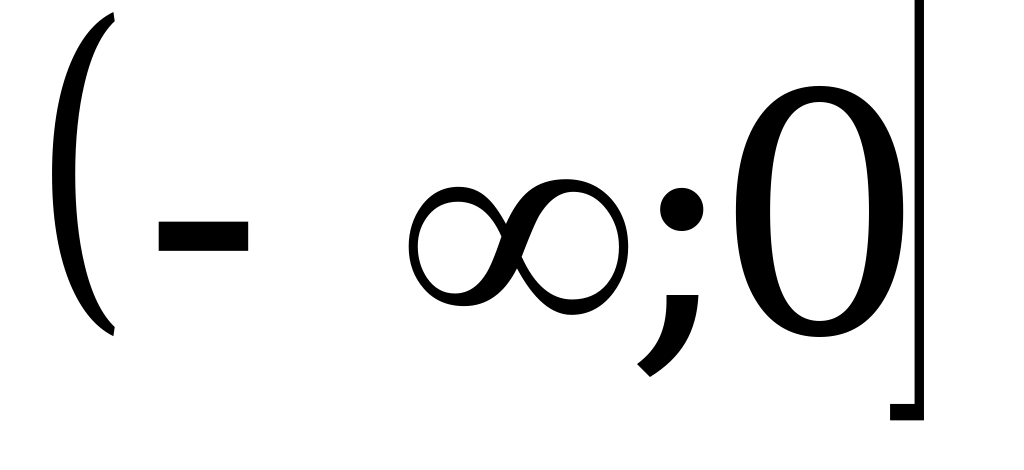 ?
?
№ 7. Функция f(x) возрастает, сравните:
А)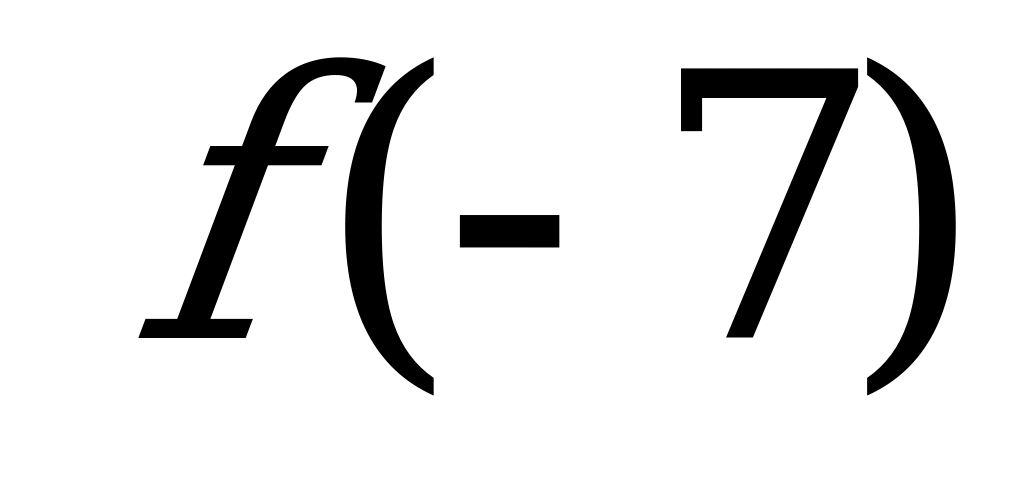 и
и 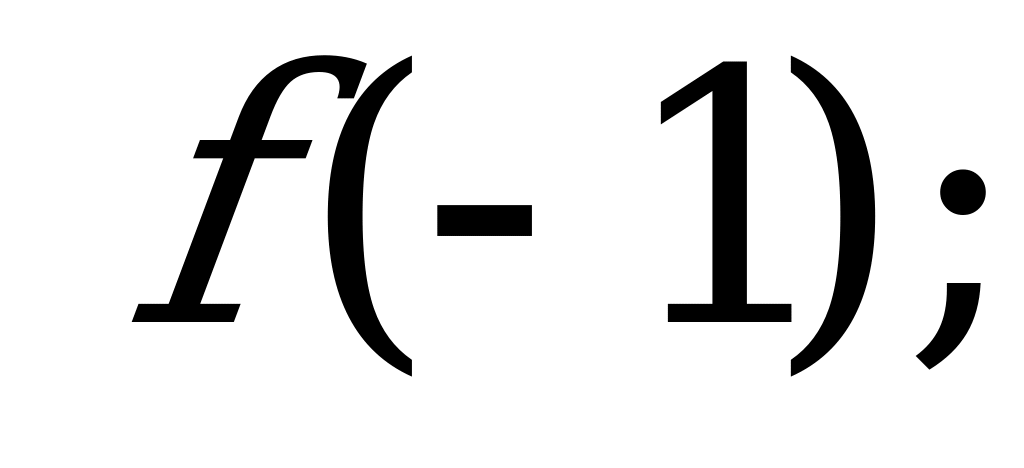 б)
б) 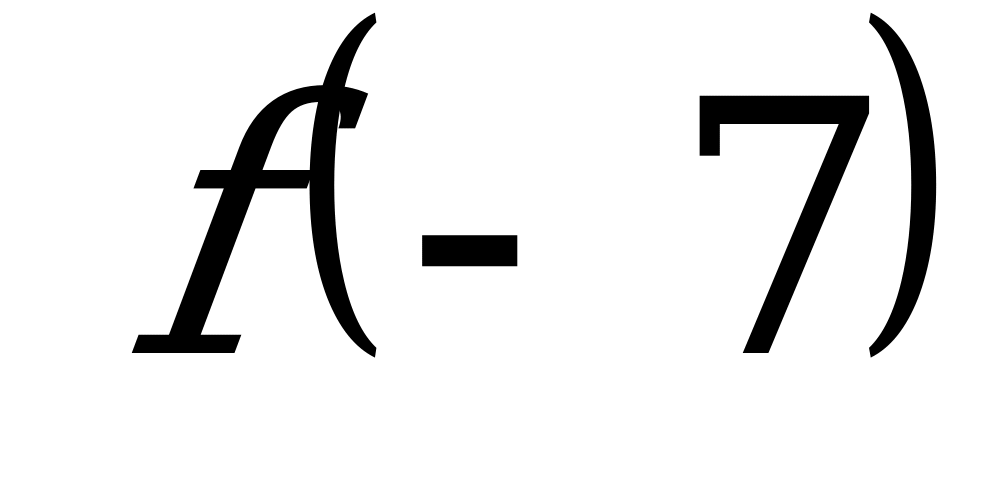 и
и 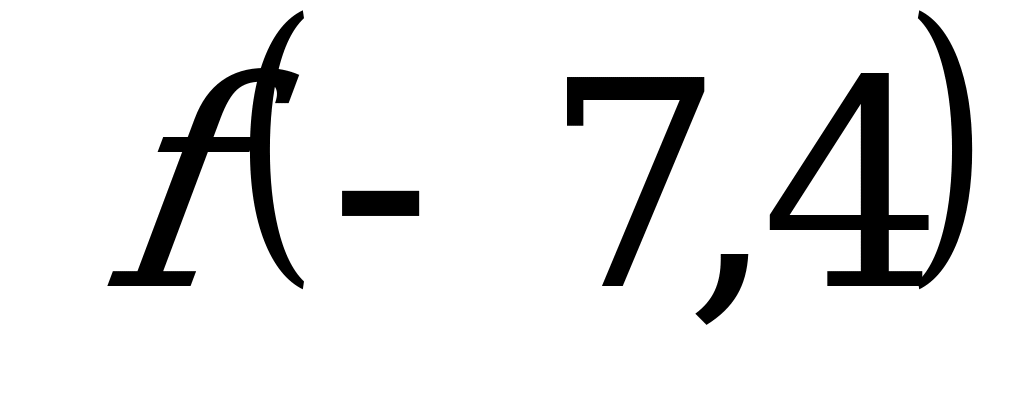
№ 8. При помощи элементарных преобразований построить график функции:
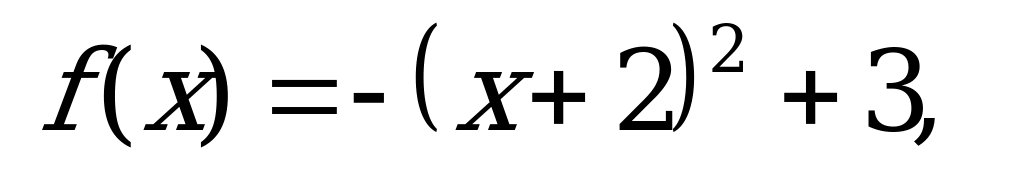
Вариант 3
№ 1. Дан график некоторой функции 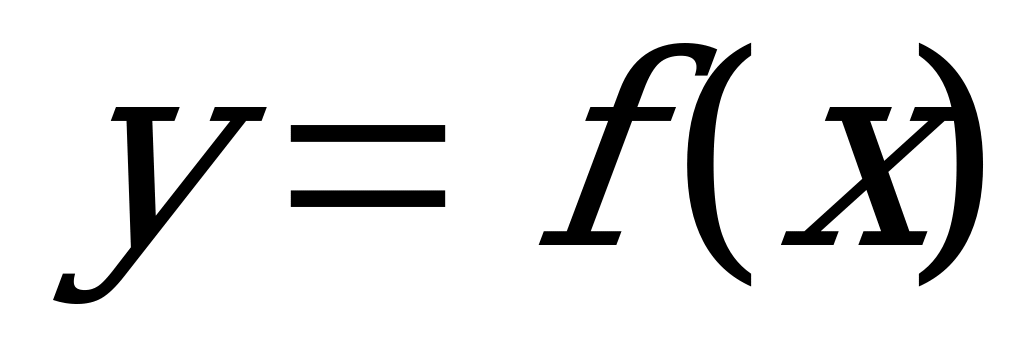
| 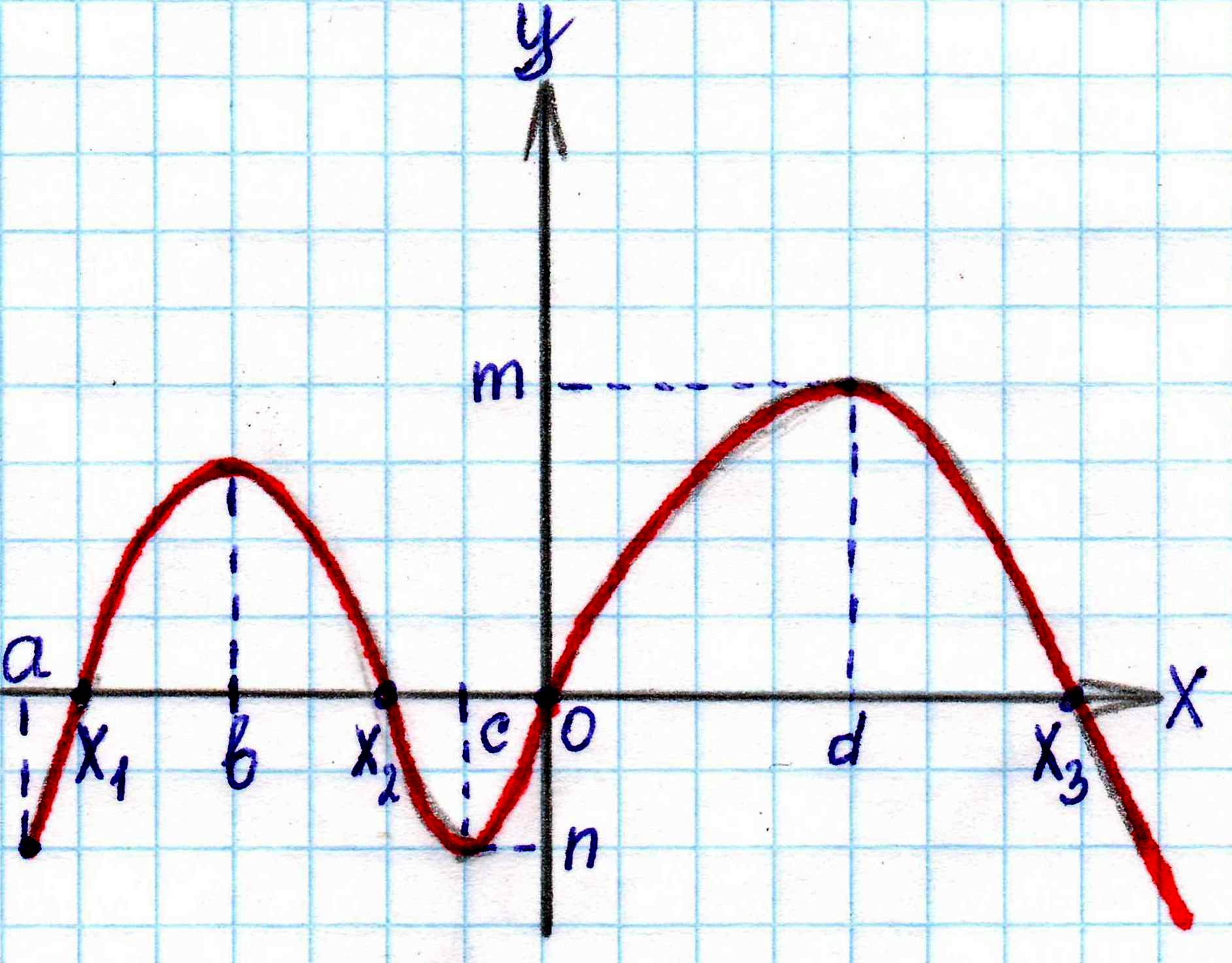
| Запишите: а) D(y), E(y); б) промежутки возрастания, убывания; в) промежутки где 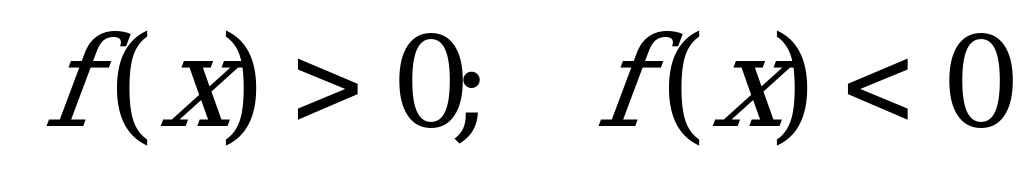 ; ; г) точки, в которых f(x) = 0; д) укажите является ли данная функция четной, нечетной или общего вида.
|
№ 2. Найдите значение функции в точке:
А)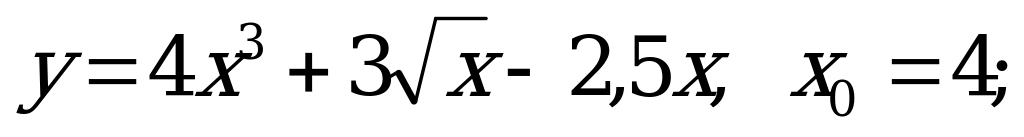 б)
б) 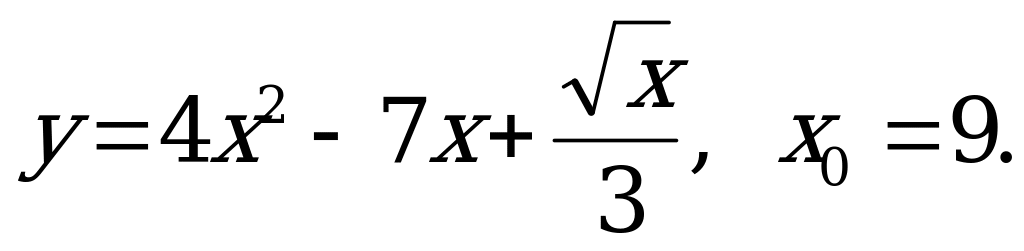
№ 3. Найдите область определения функций:
А) 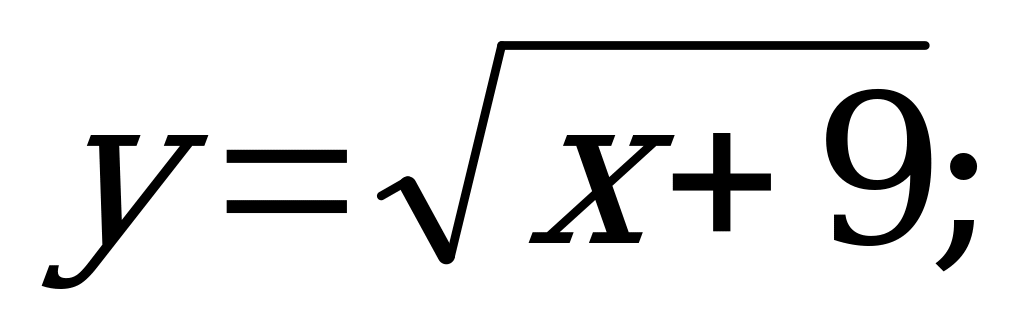 б)
б)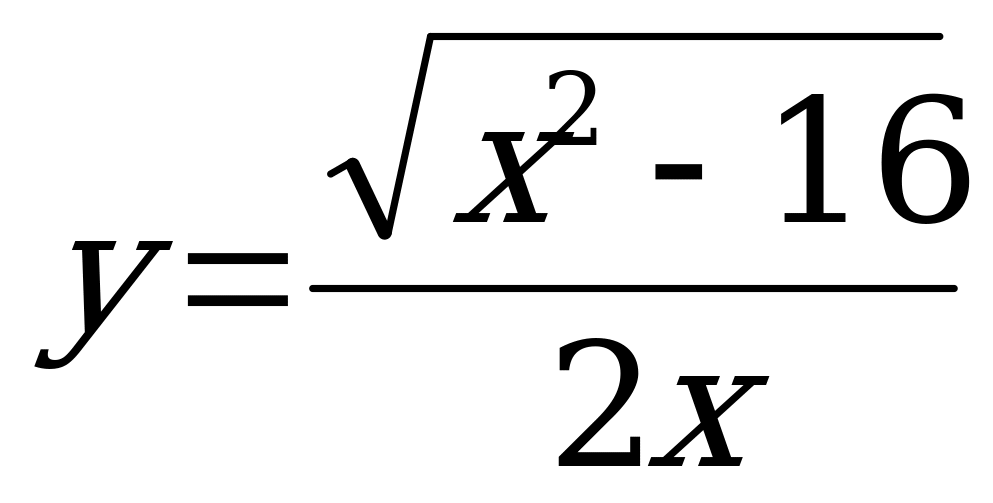
№ 4. Найдите обратную функцию:
А) 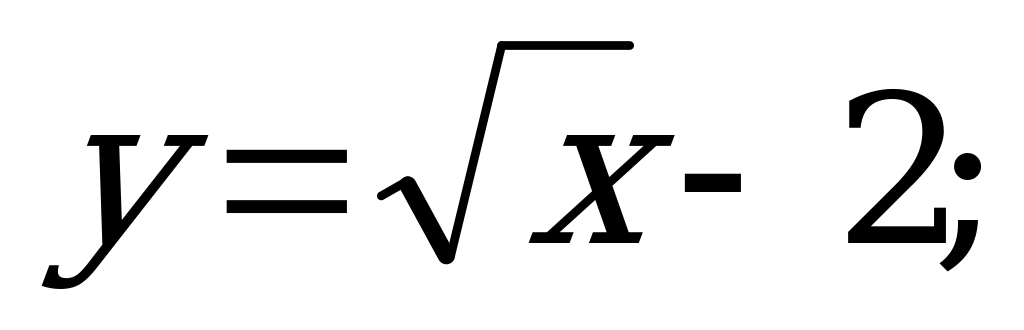 б)
б) 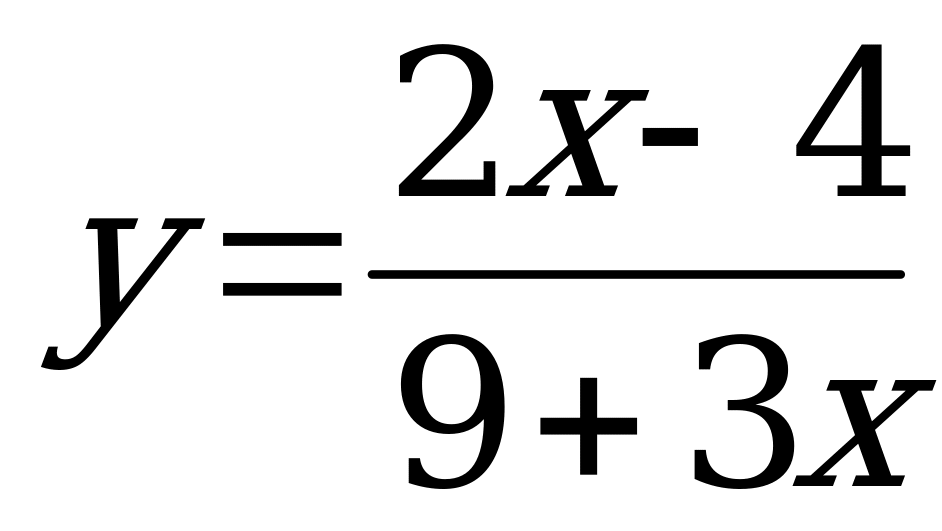
№ 5. Выполните действия над функциями: 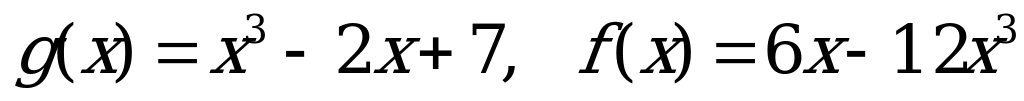
А)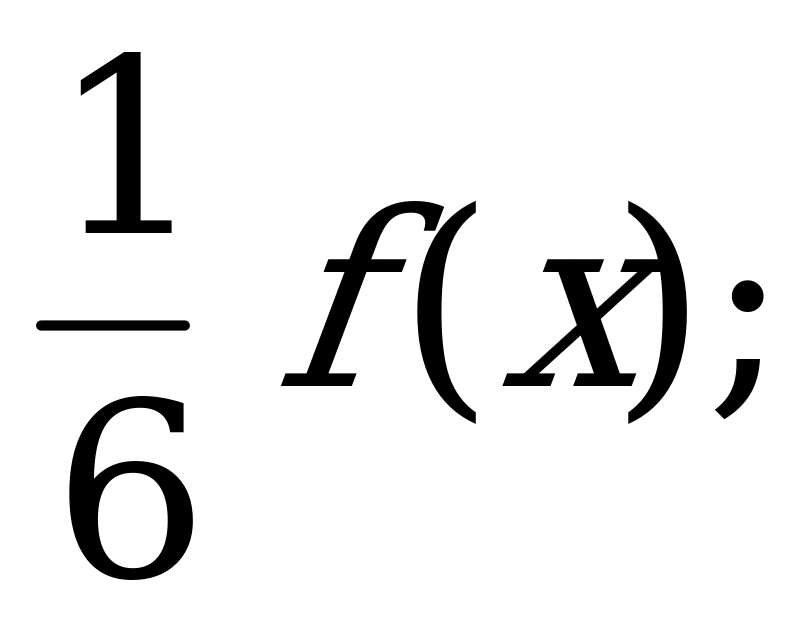 б)
б)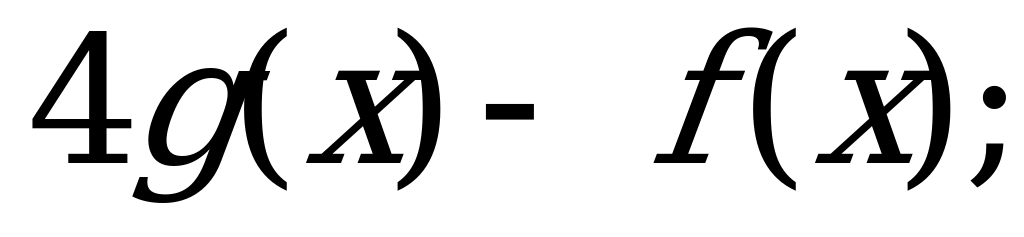 в)
в) 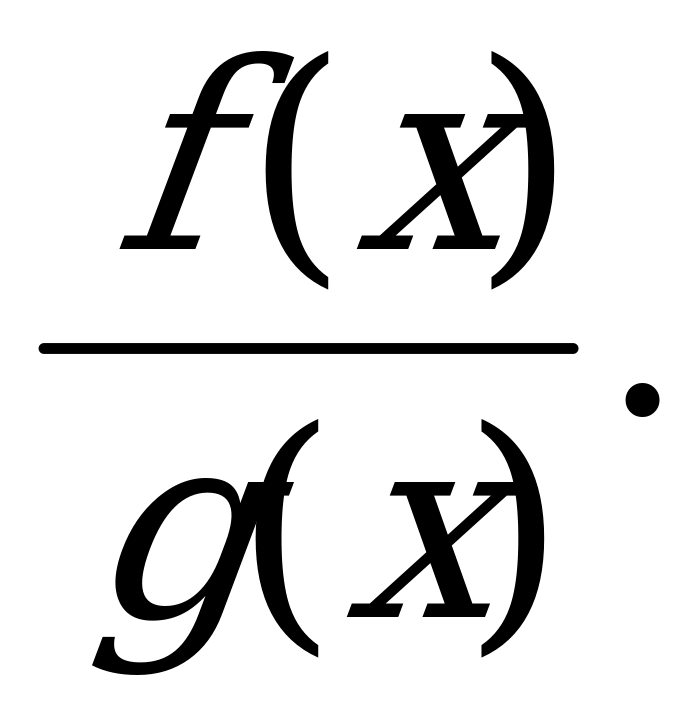
№ 6. Найдите n, если известно, что график функции 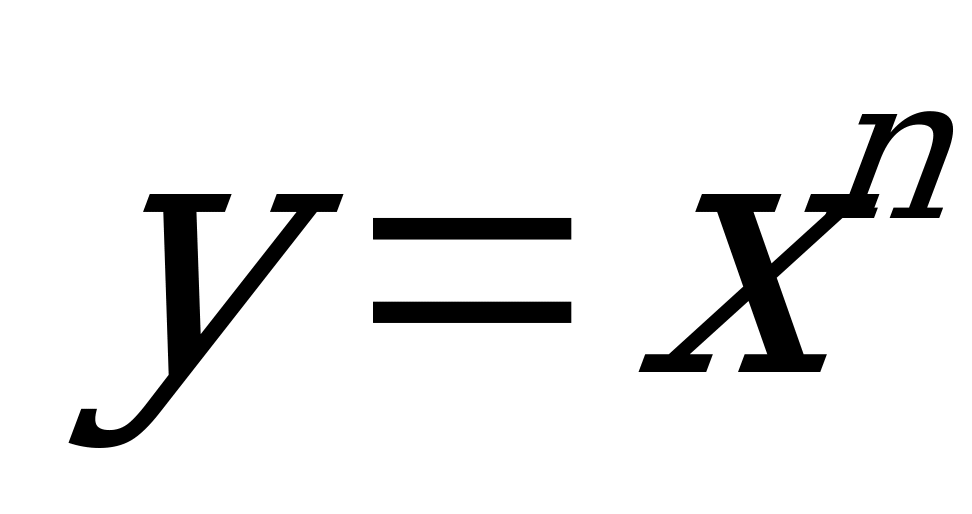 проходит через точку С(-3; 81)
проходит через точку С(-3; 81)
№ 7. Функция f(x) убывающая, сравните:
А)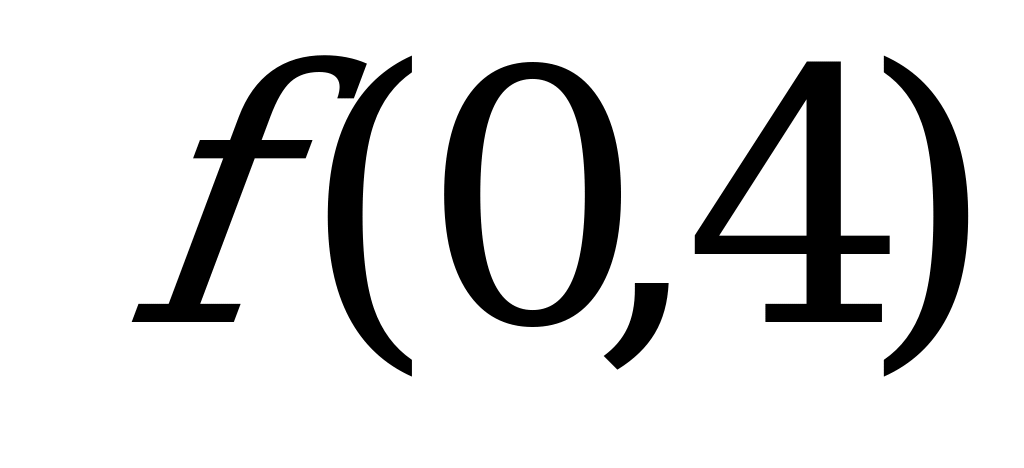 и
и 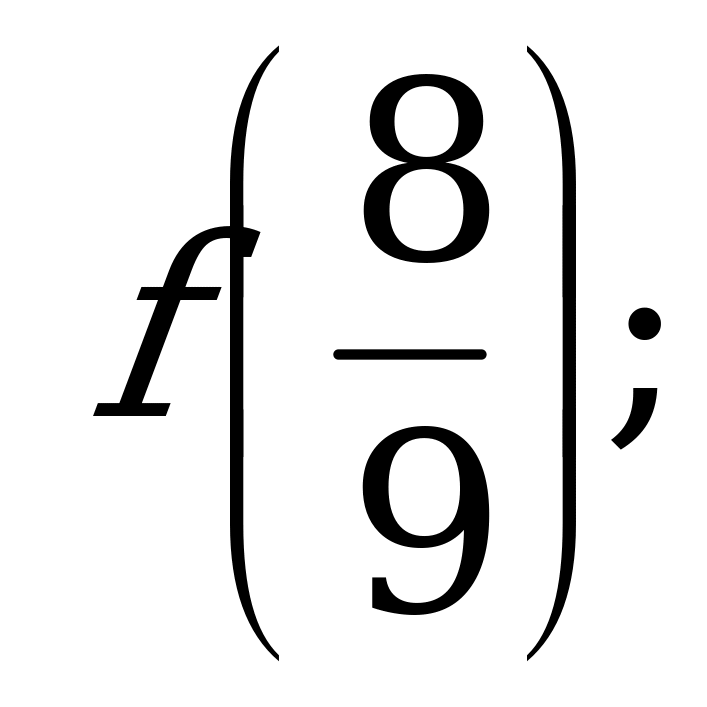 б)
б)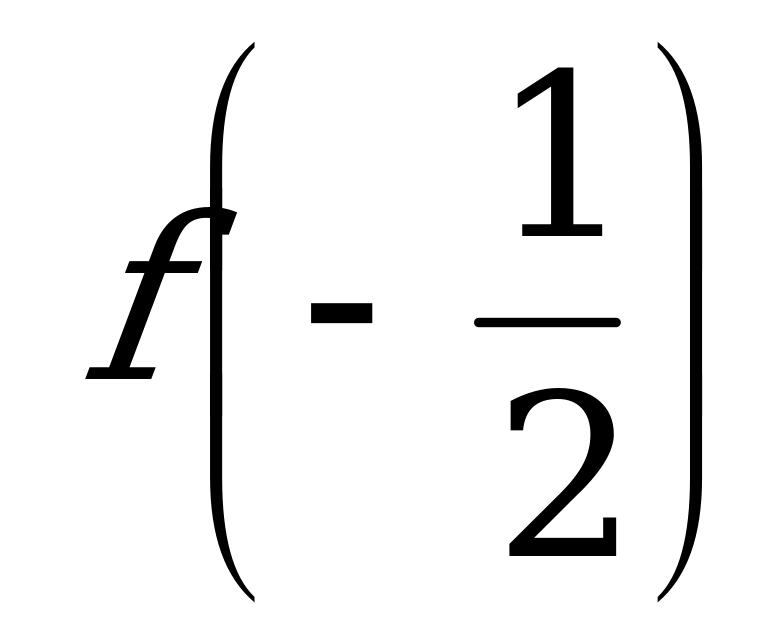 и
и 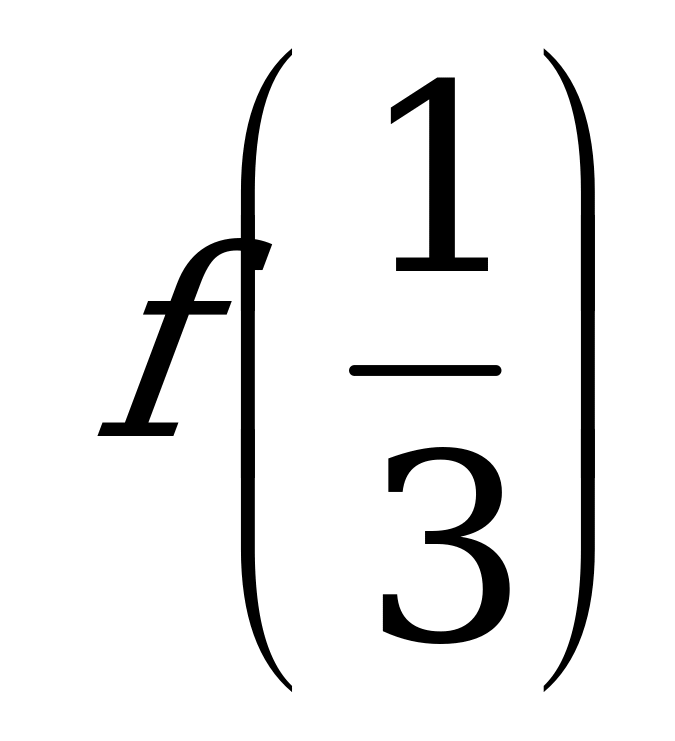
№ 8 Построить график функции с помощью элементарных преобразований:
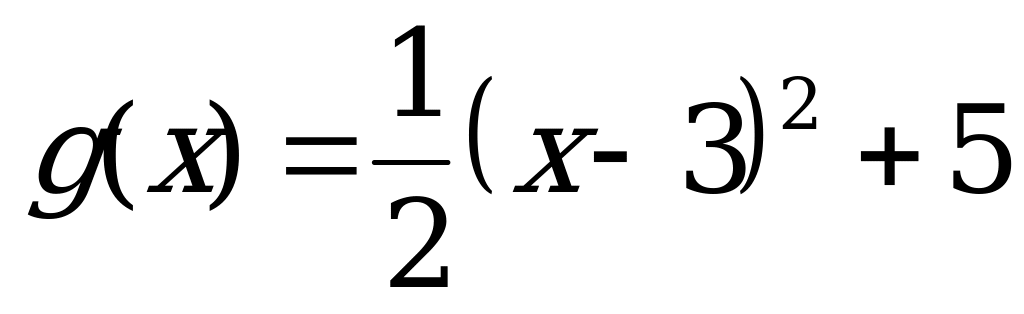
Вариант 4
№ 1. Дан график некоторой функции 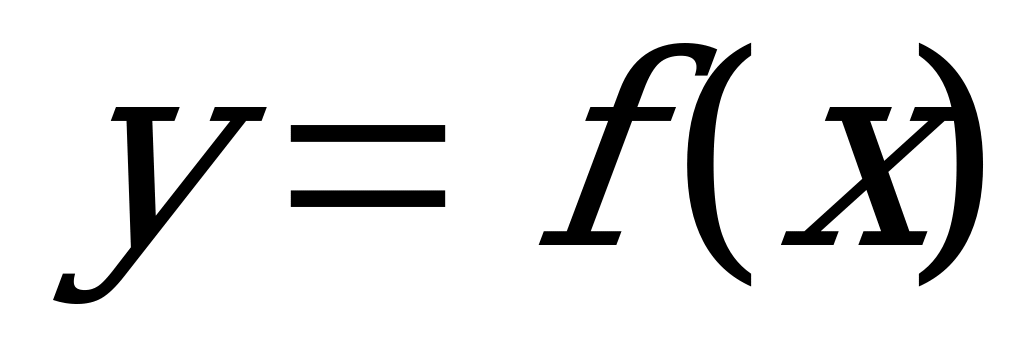
| 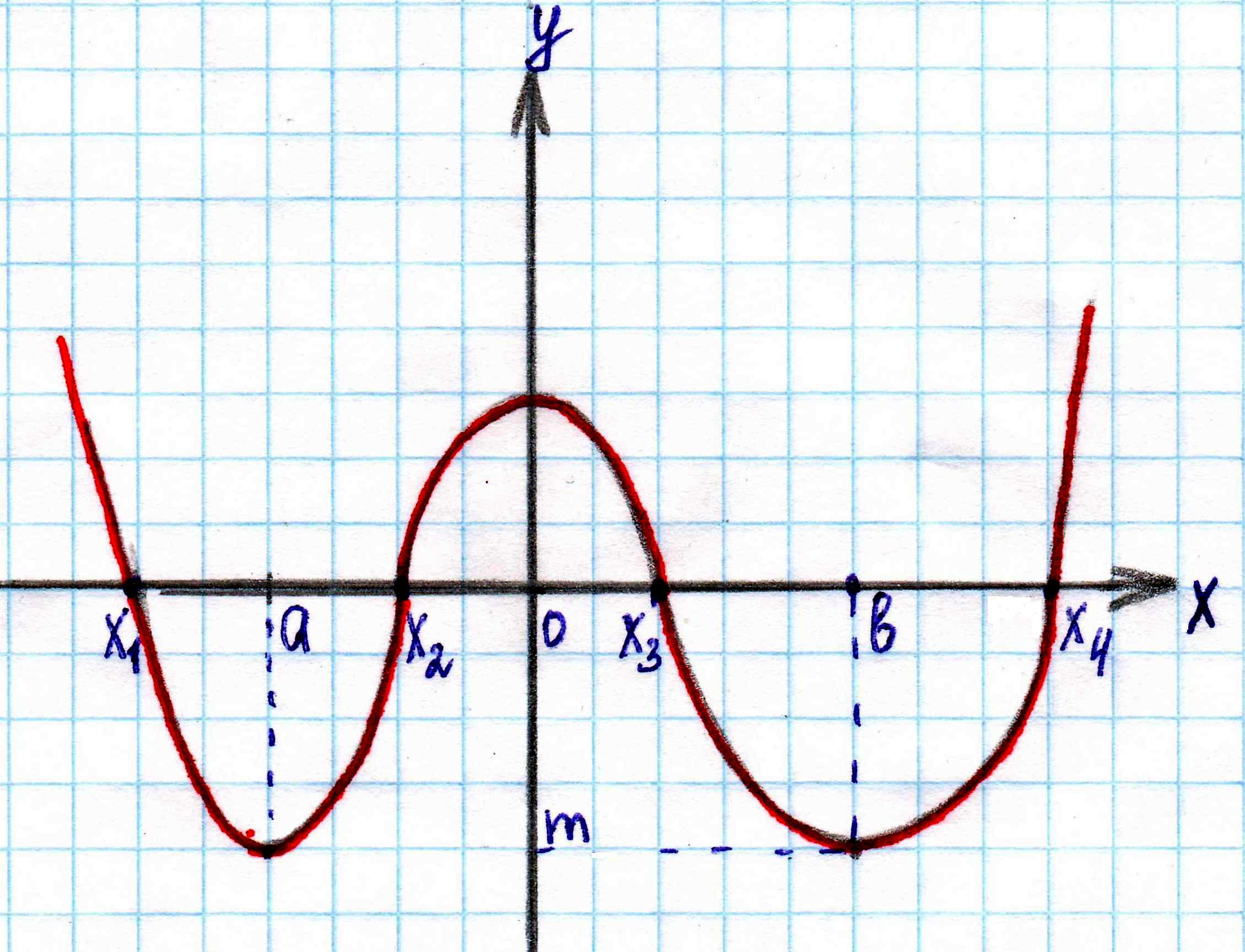
| Запишите: а) D(y), E(y); б) промежутки возрастания, убывания; в) промежутки где 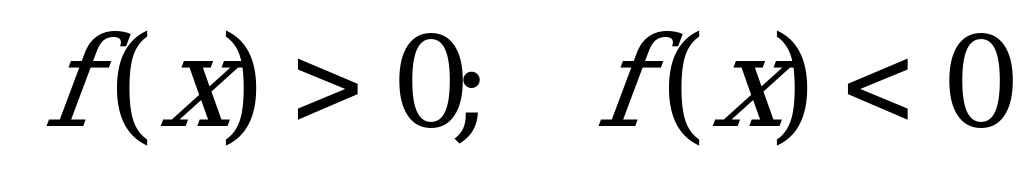 ; ; г) точки, в которых f(x) = 0; д) укажите является ли данная функция четной, нечетной или общего вида.
|
№ 2. Найдите значение функции в точке:
А)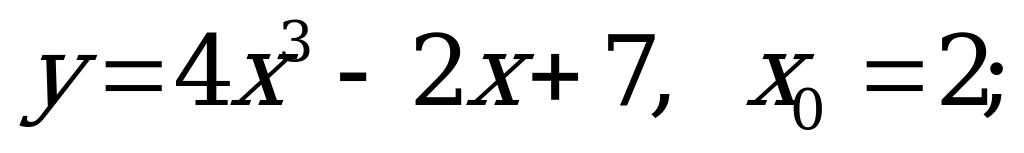 б)
б) 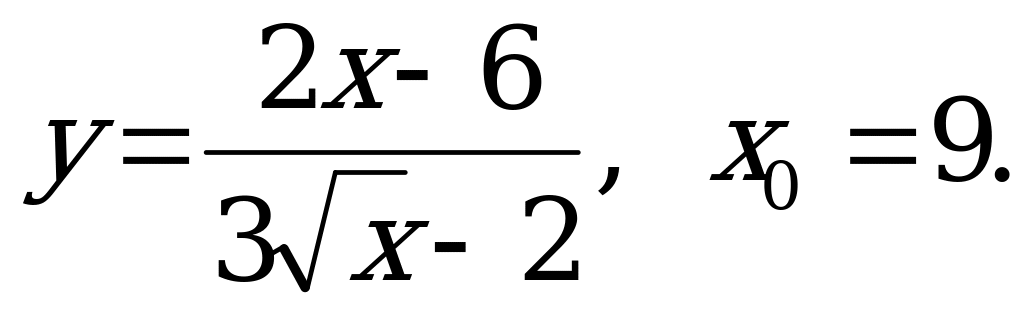
№ 3. Найдите область определения функций:
А)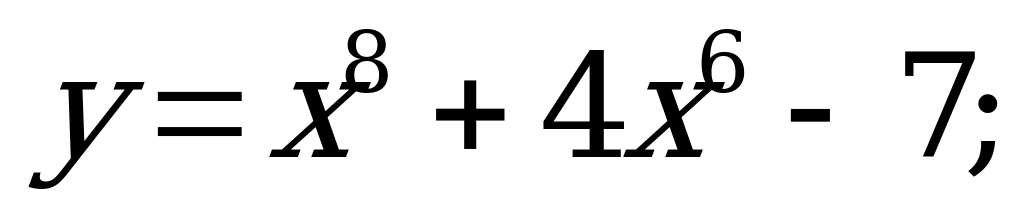 б)
б)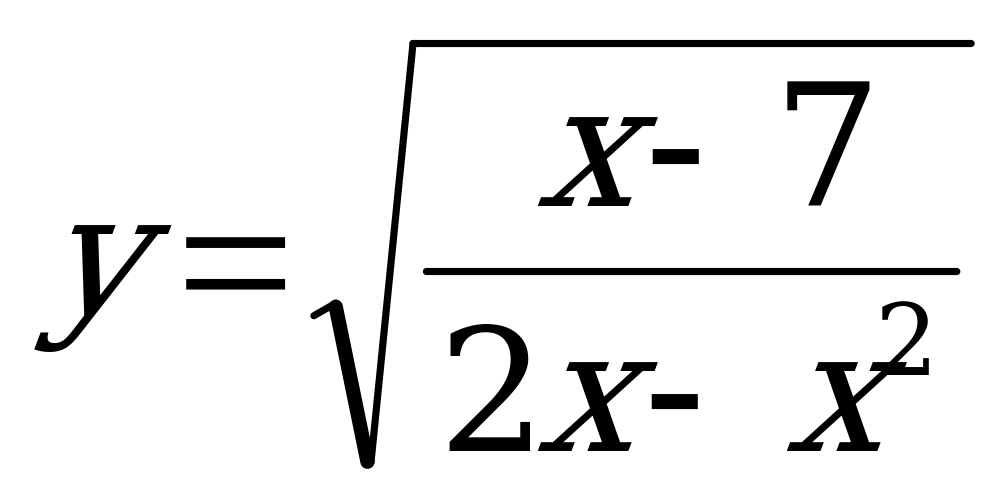
№ 4. Найдите обратную функцию:
А)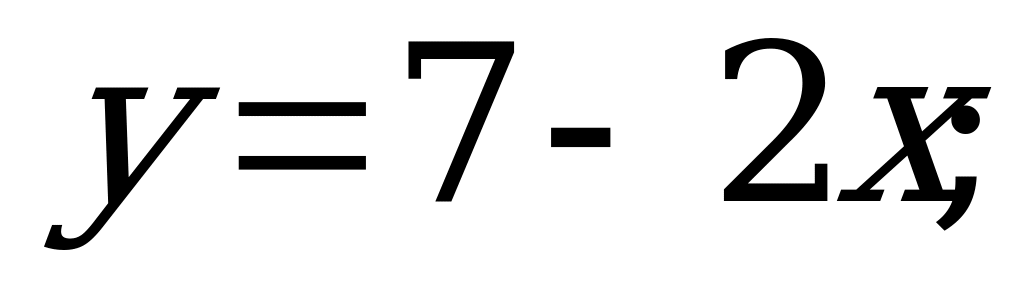 б)
б) 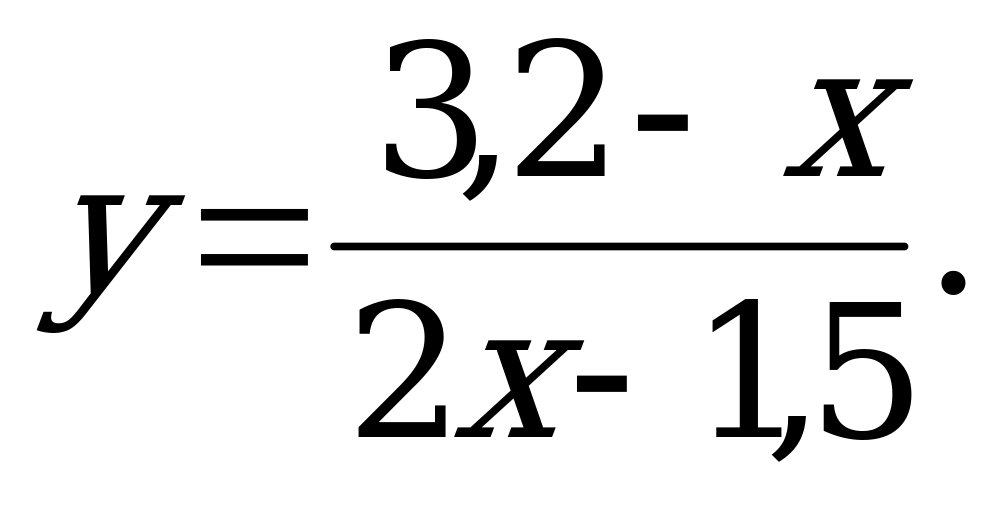
№ 5. Выполните действия над функциями: 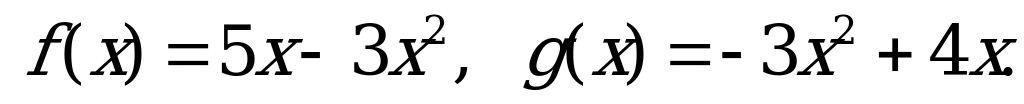
А)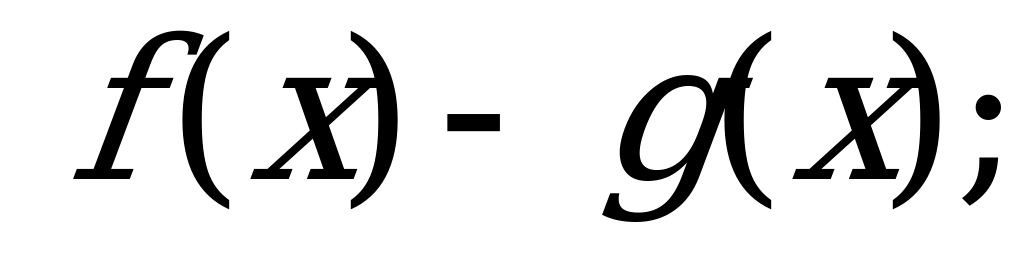 б)
б) 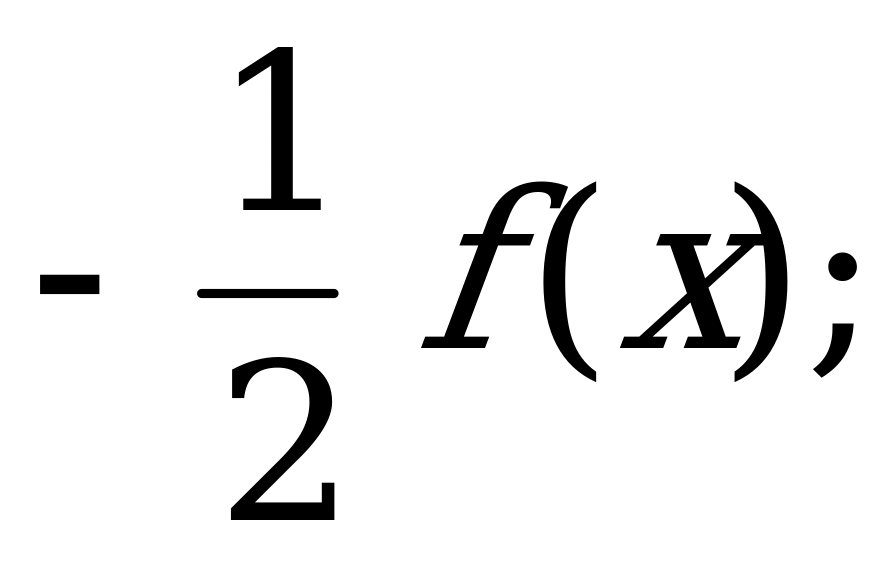 в)
в) 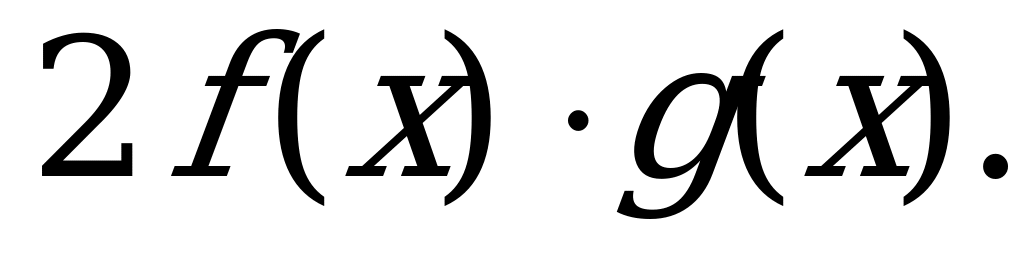
№ 6. Принадлежит ли графику функции 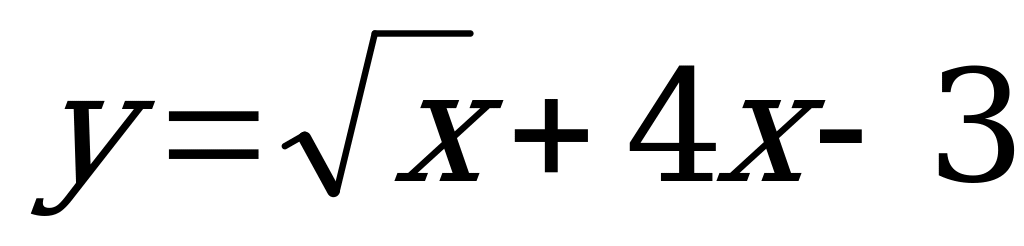 точка М(9; 35)
точка М(9; 35)
№ 7 Функция f(x) возрастающая, сравните:
А)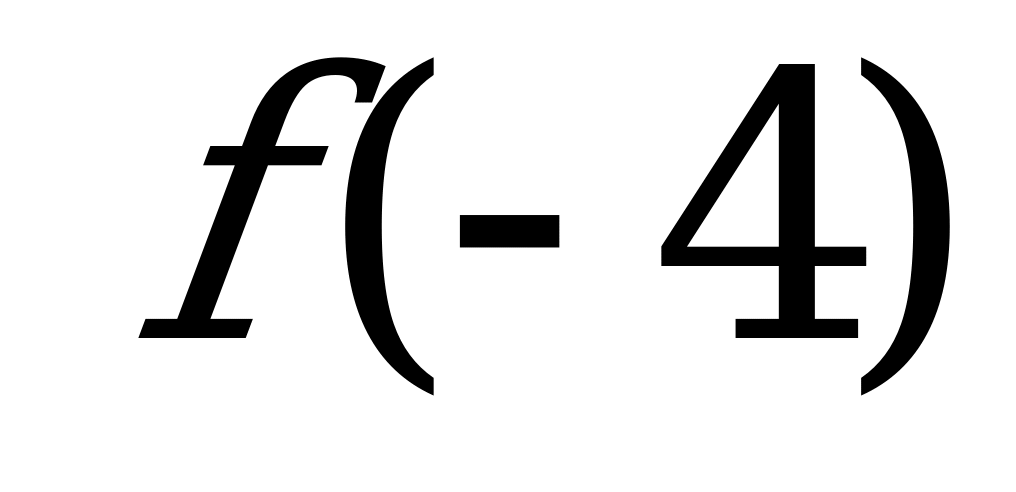 и
и 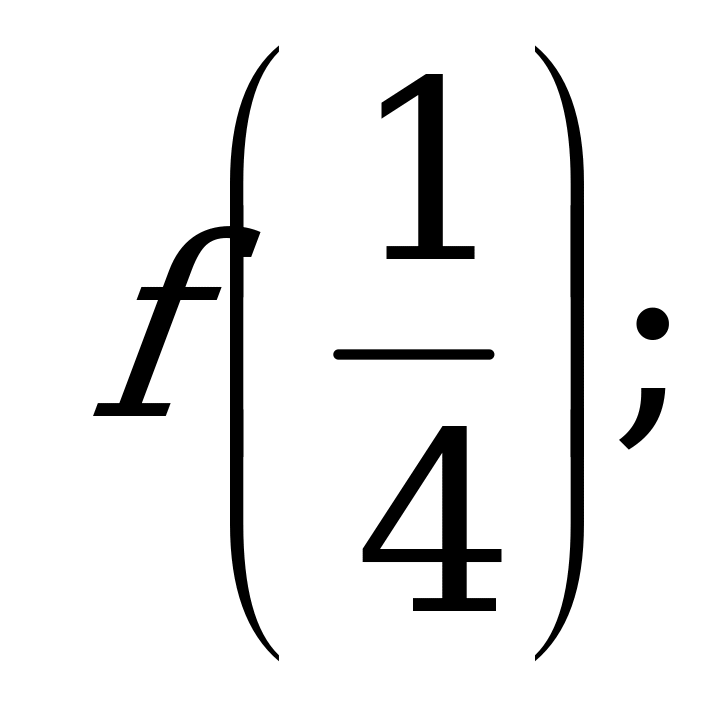 б)
б) 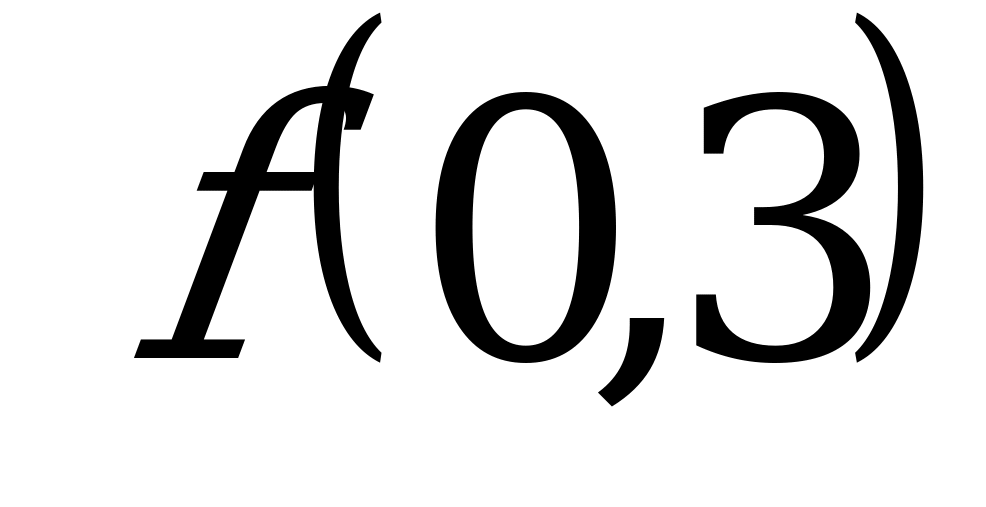 и
и 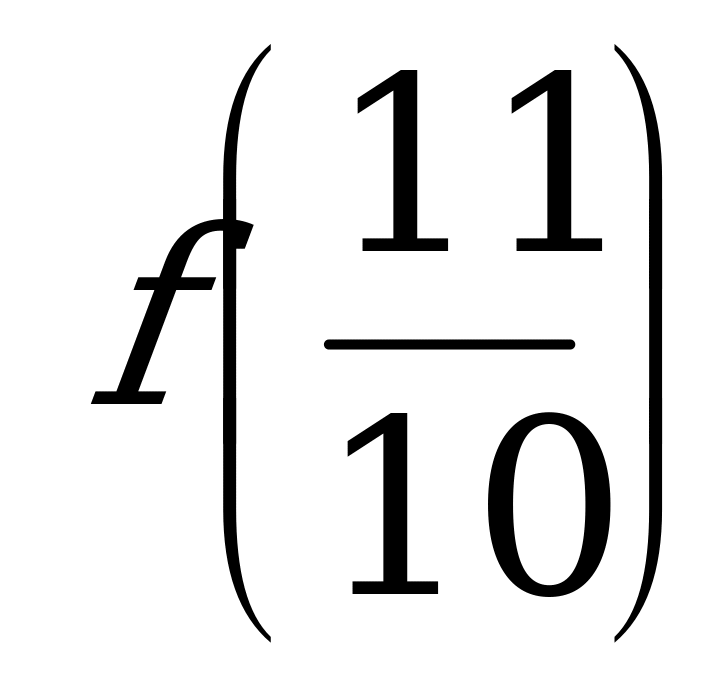
№ 8 Построить график функции с помощью элементарных преобразований:
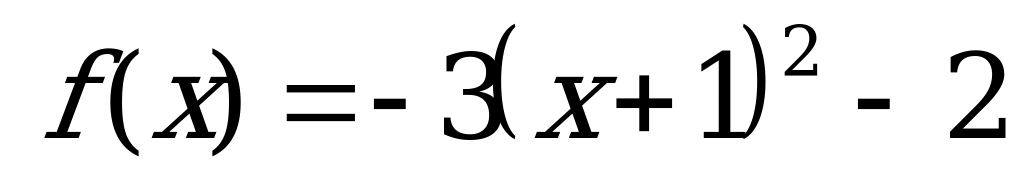
Вариант 5
№ 1. Дан график некоторой функции 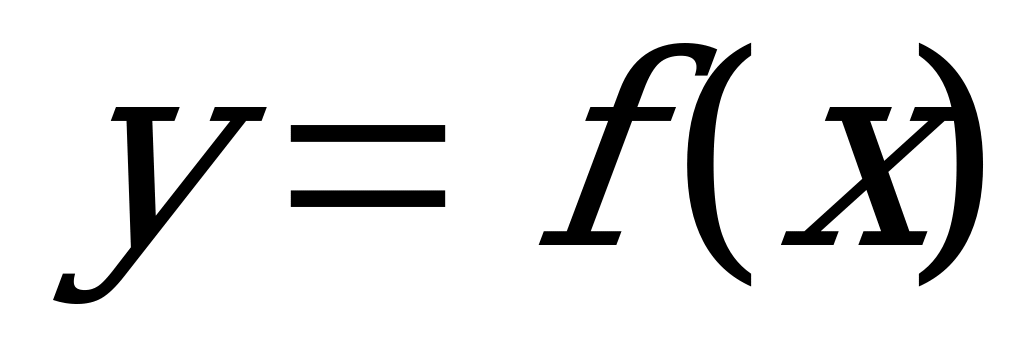
| 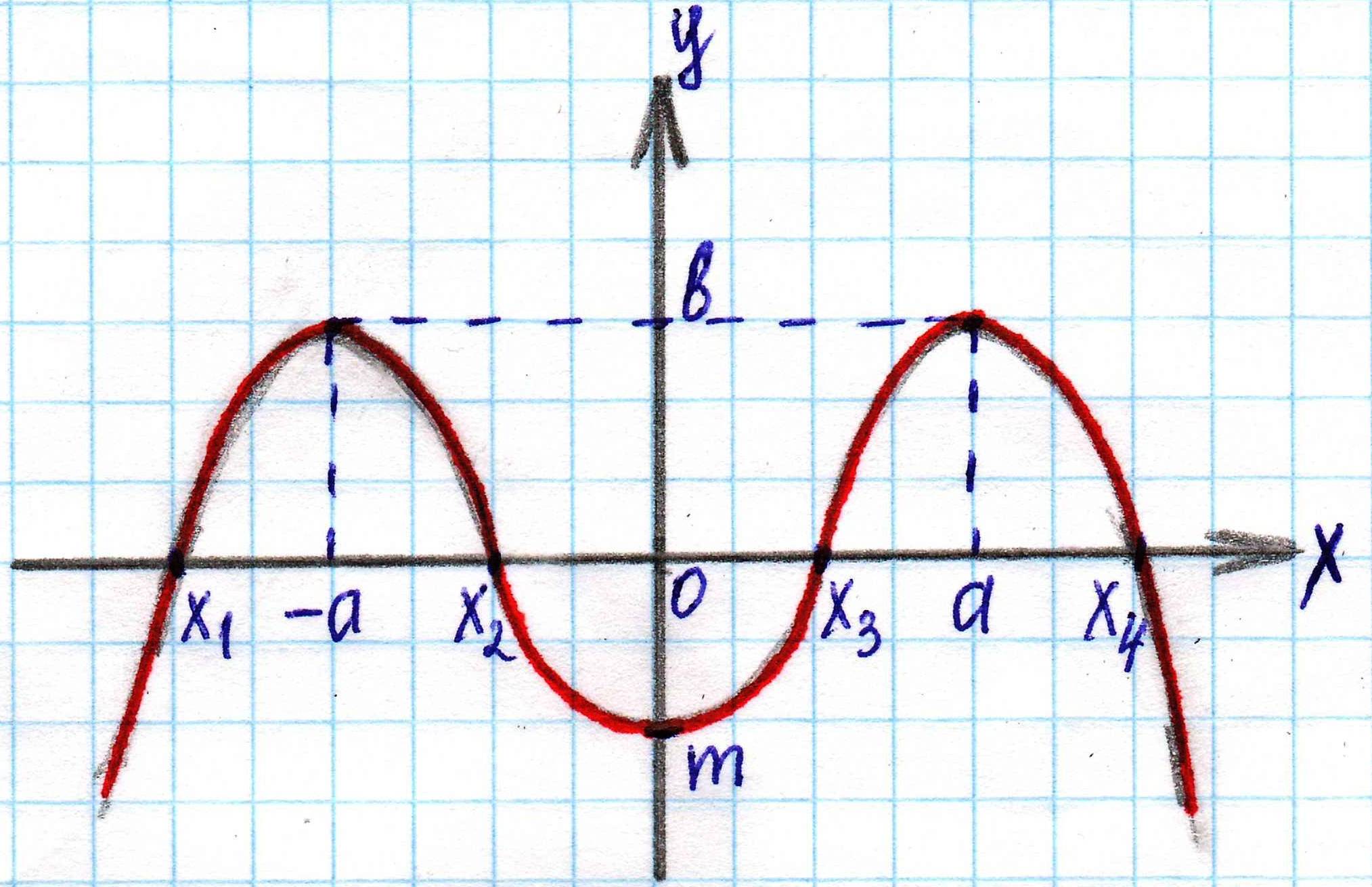
| Запишите: а) D(y), E(y); б) промежутки возрастания, убывания; в) промежутки где 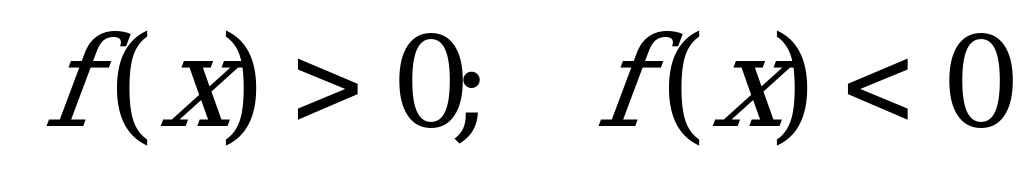 ; ; г) точки, в которых f(x) = 0; д) укажите является ли данная функция четной, нечетной или общего вида.
|
№ 2. Найдите значение функции в точке:
А)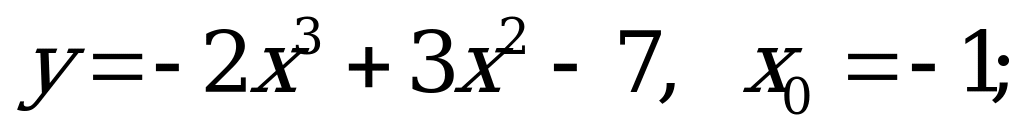 б)
б) 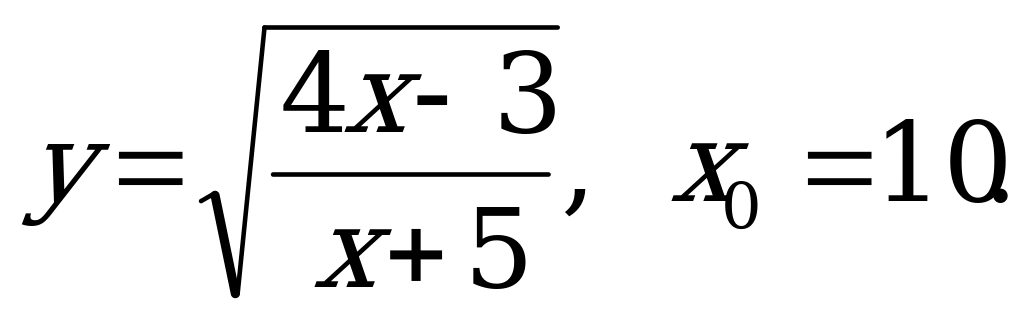
№ 3. Найдите область определения функций:
А)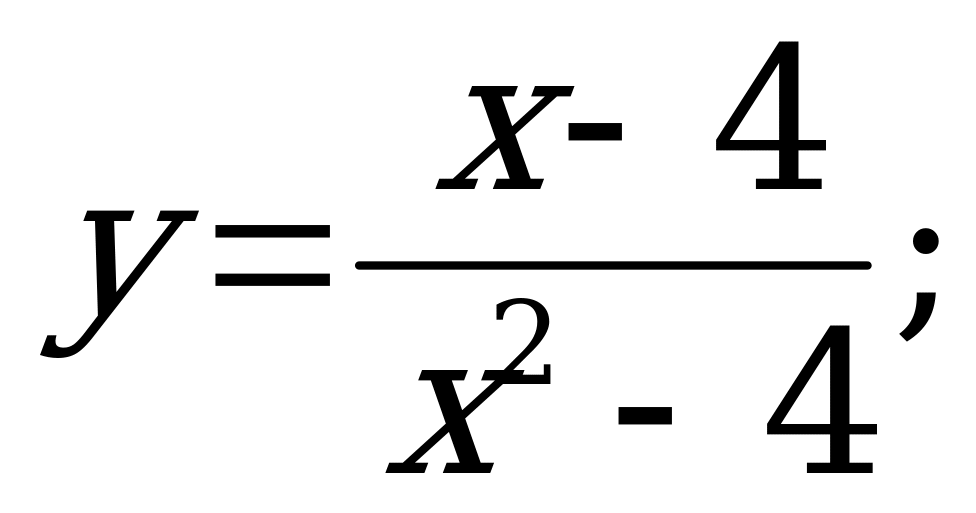 б)
б)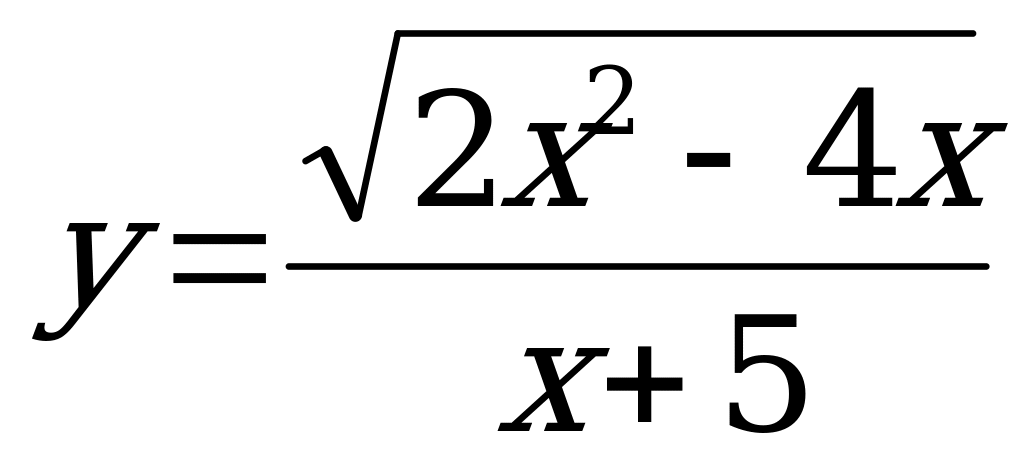
№ 4. Найдите обратную функцию:
А)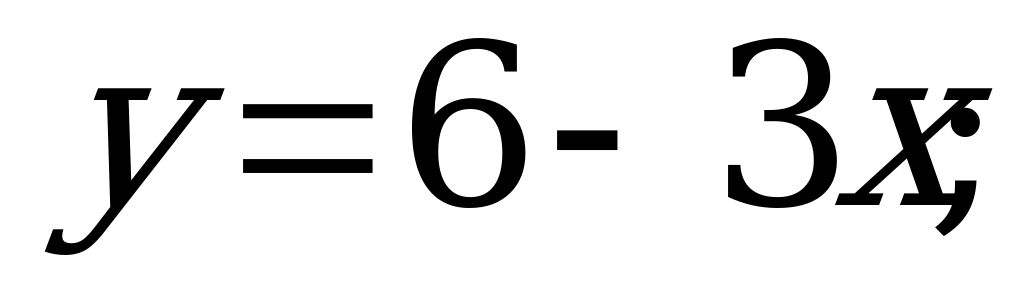 б)
б)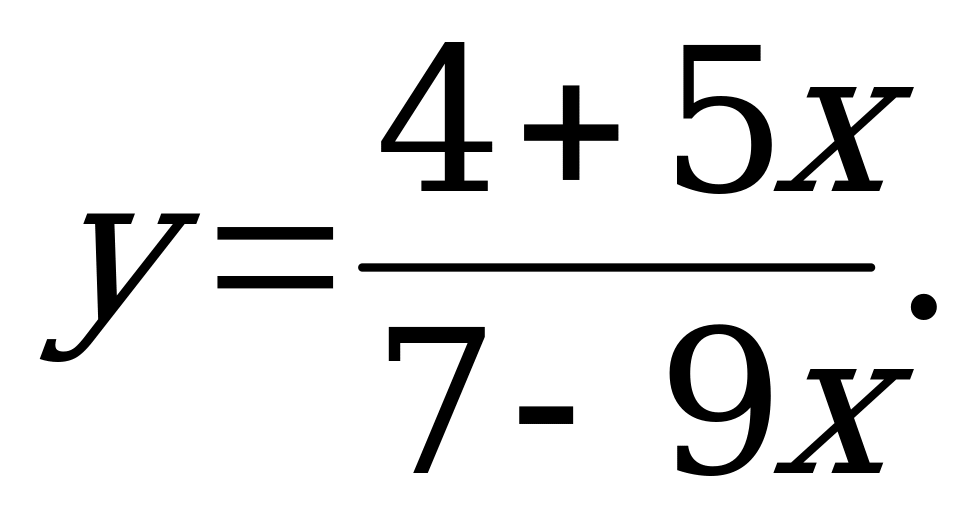
№ 5. Выполните действия над функциями: 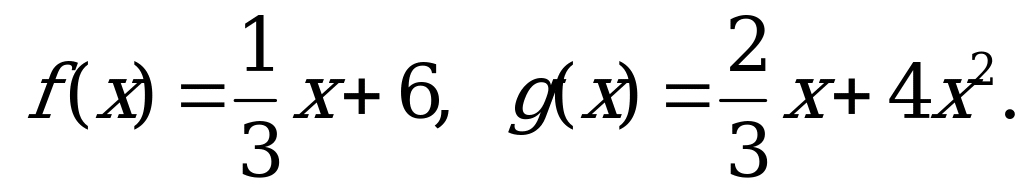
А)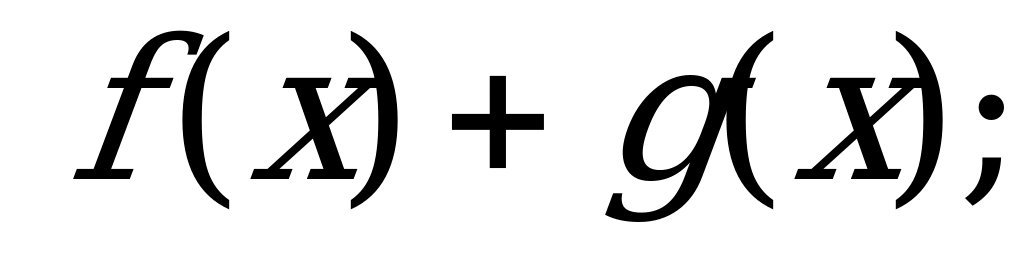 б)
б) 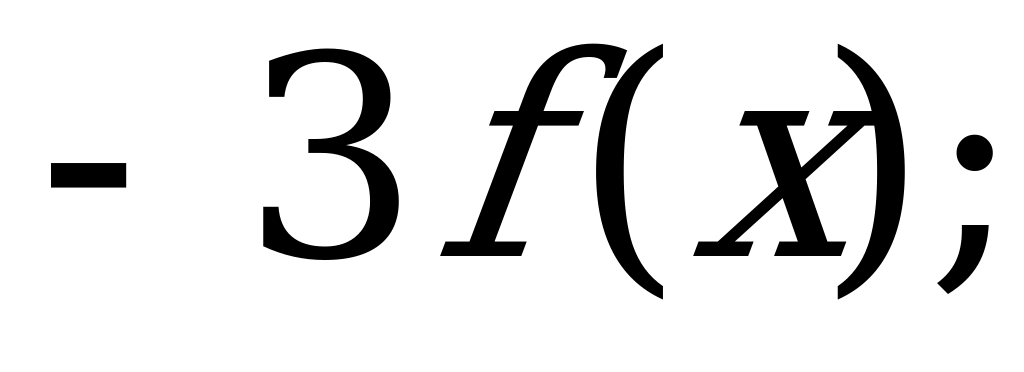 в)
в)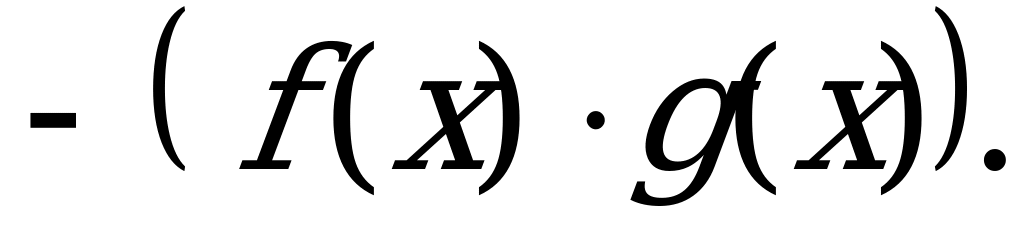
№ 6. Задайте формулой какую-либо квадратичную функцию, которая в промежутке 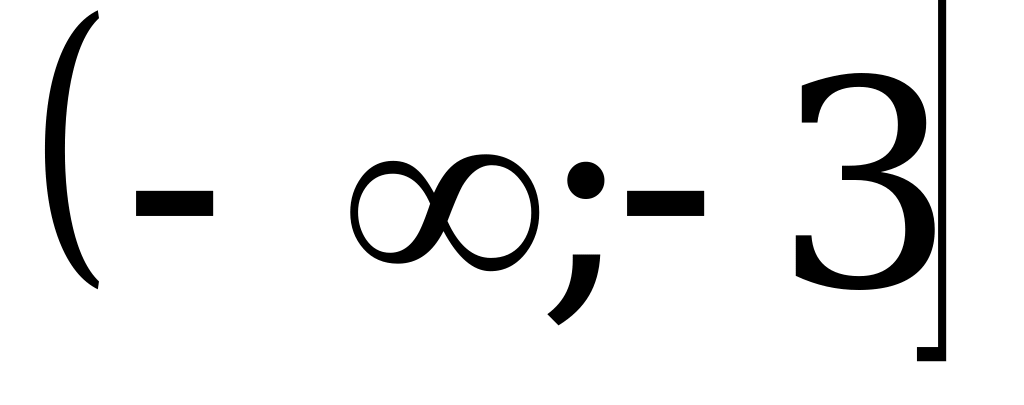 убывает, а в промежутке
убывает, а в промежутке 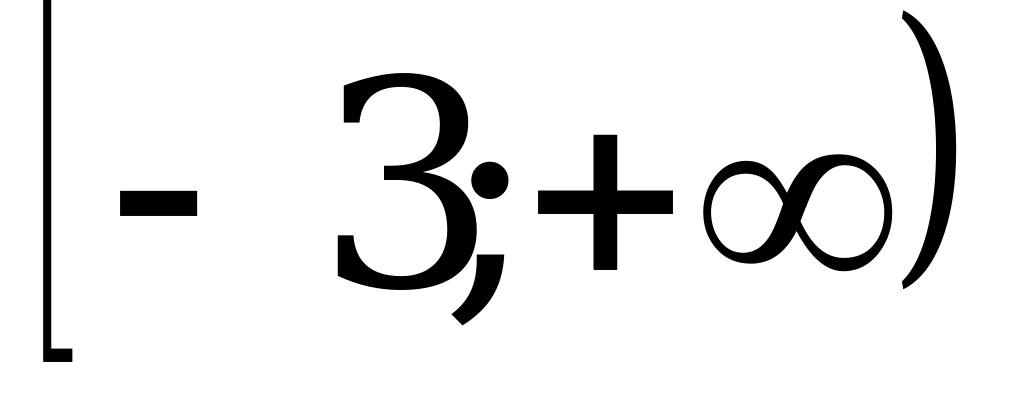 возрастает.
возрастает.
№ 7 Функция f(x) убывающая, сравните:
А)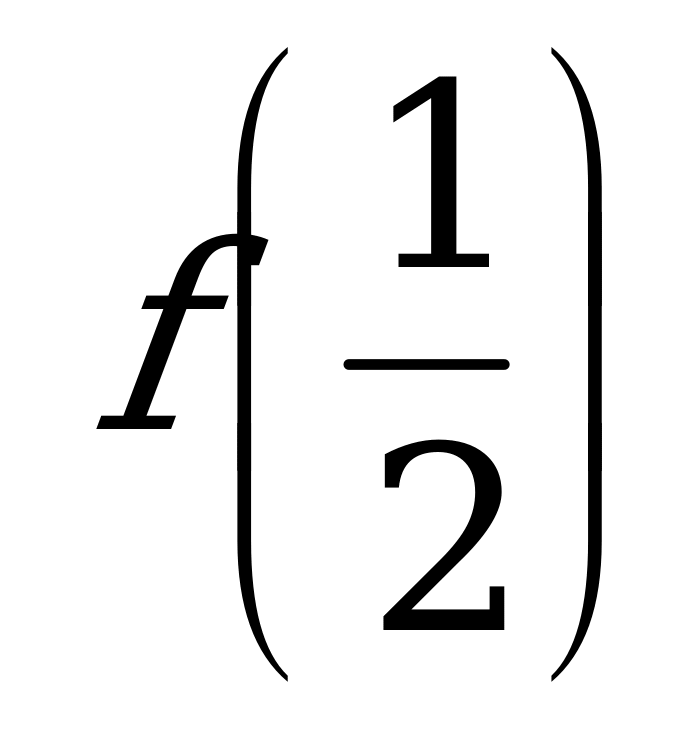 и
и 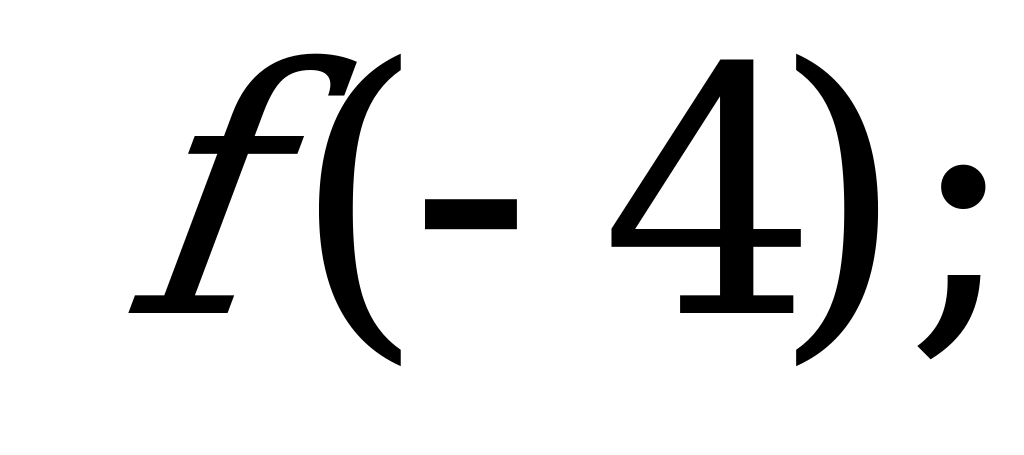 б)
б) 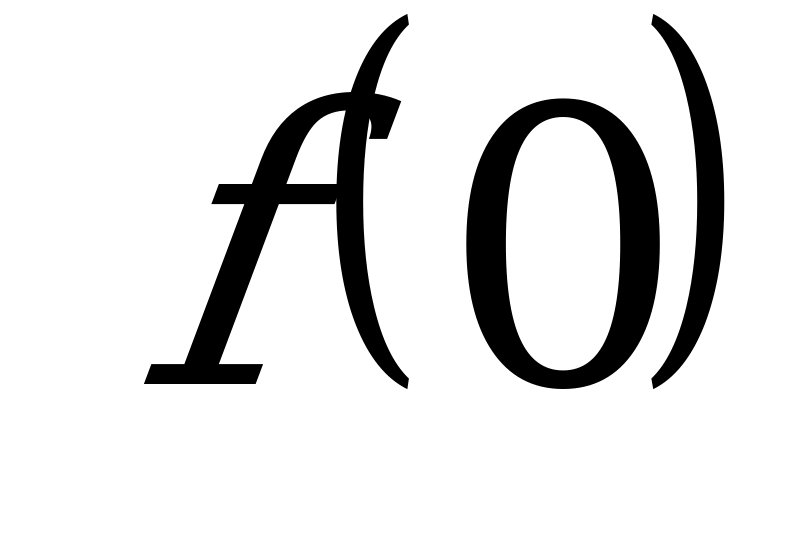 и
и 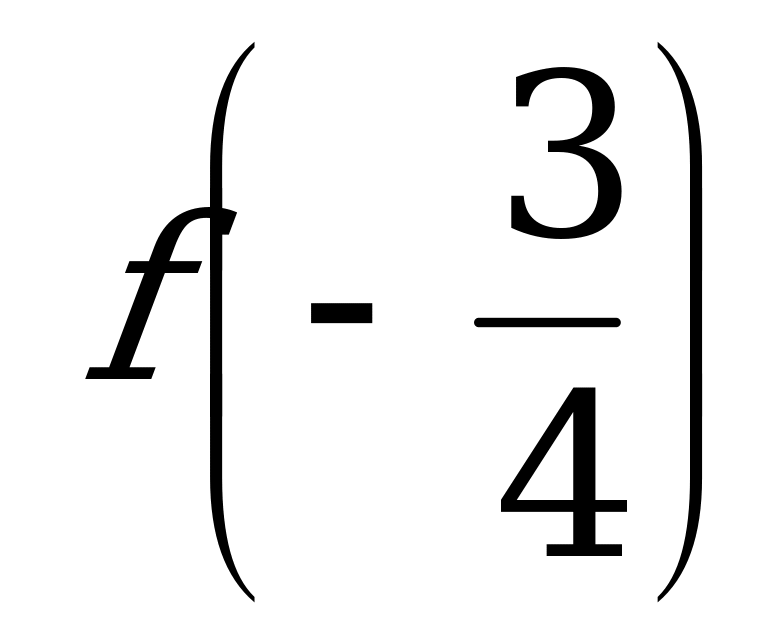
№ 8. Построить график с помощью элементарных преобразований:
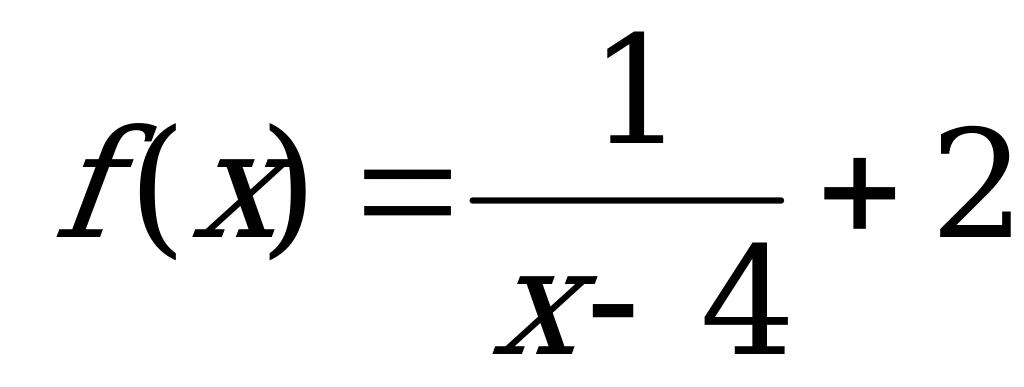
Вариант 6
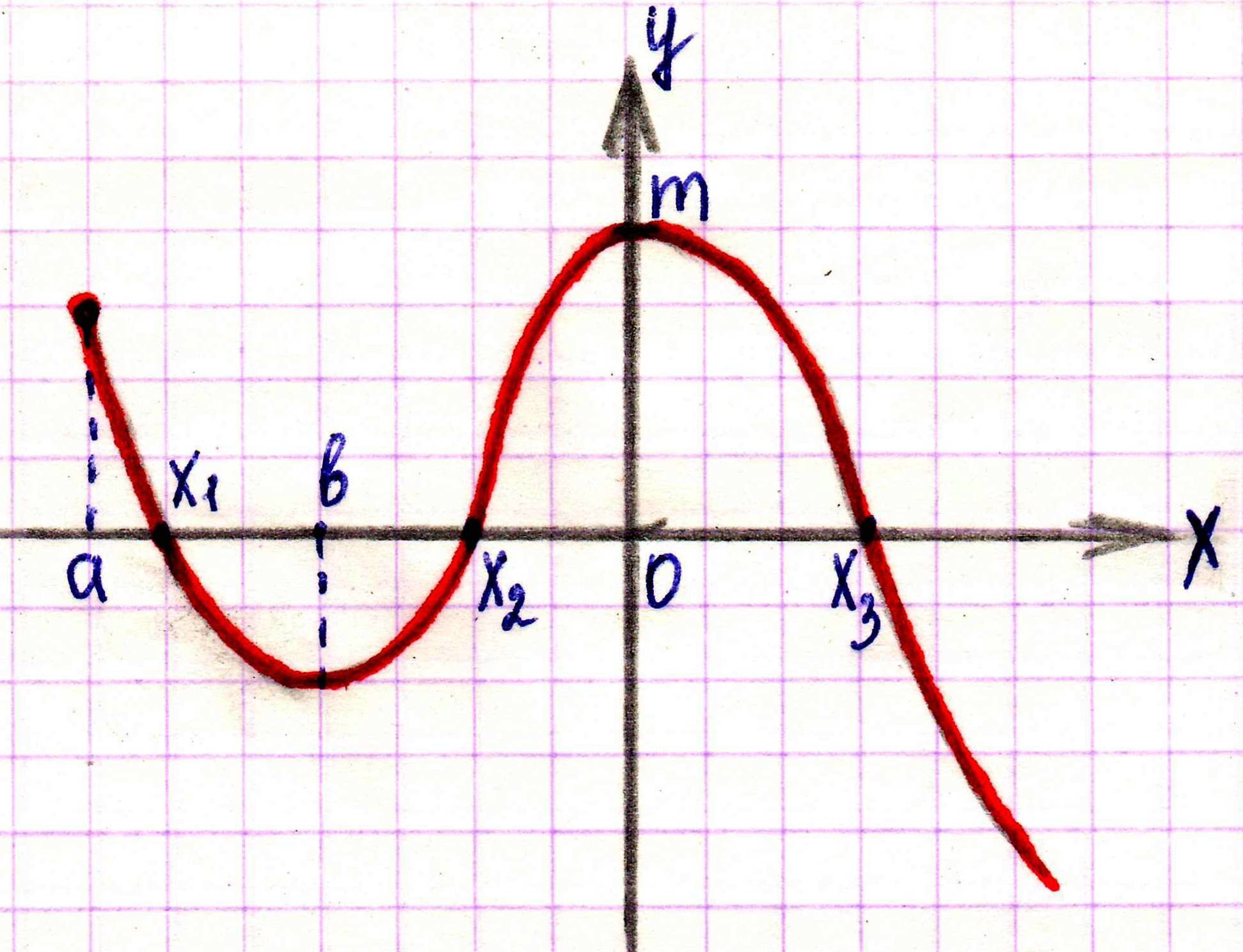
№ 1. Дан график некоторой функции 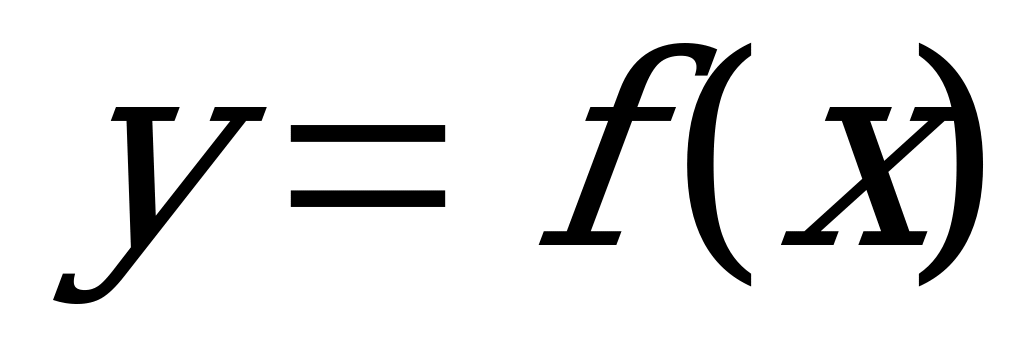
| 
|
Запишите: а) D(y), E(y); б) промежутки возрастания, убывания; в) промежутки где 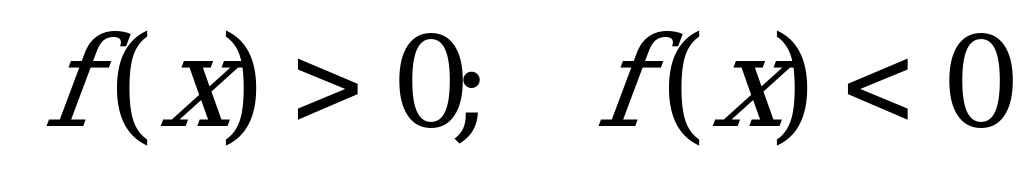 ; ; г) точки, в которых f(x) = 0; д) укажите является ли данная функция четной, нечетной или общего вида.
|
№ 2. Найдите значение функции в точке:
А)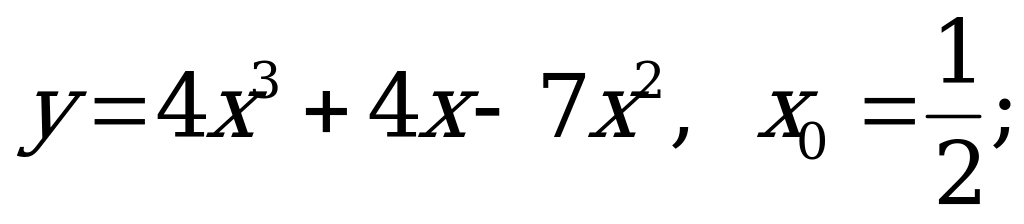 б)
б) 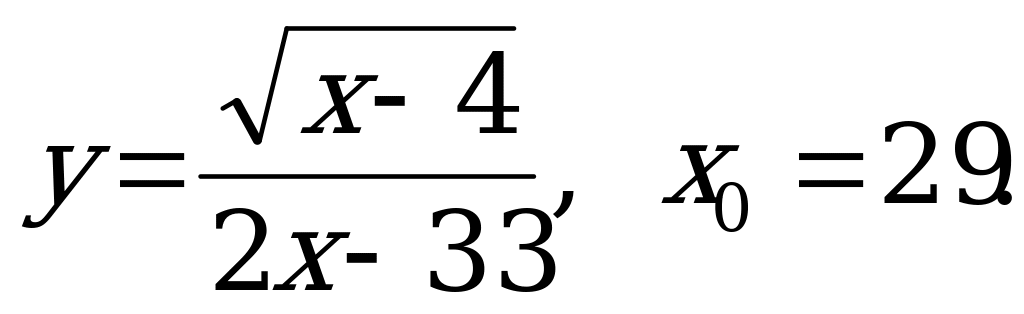
№ 3. Найдите область определения функций:
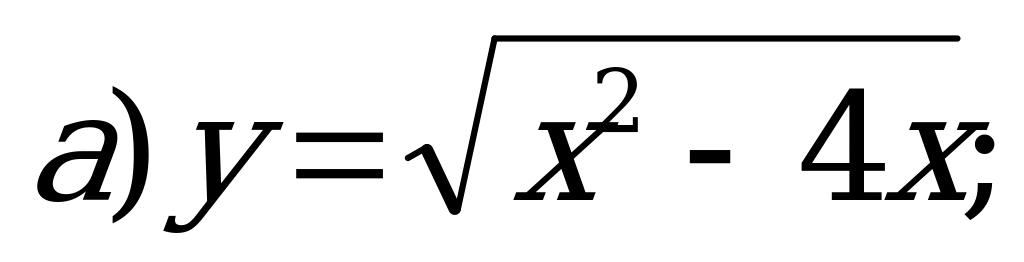 б)
б)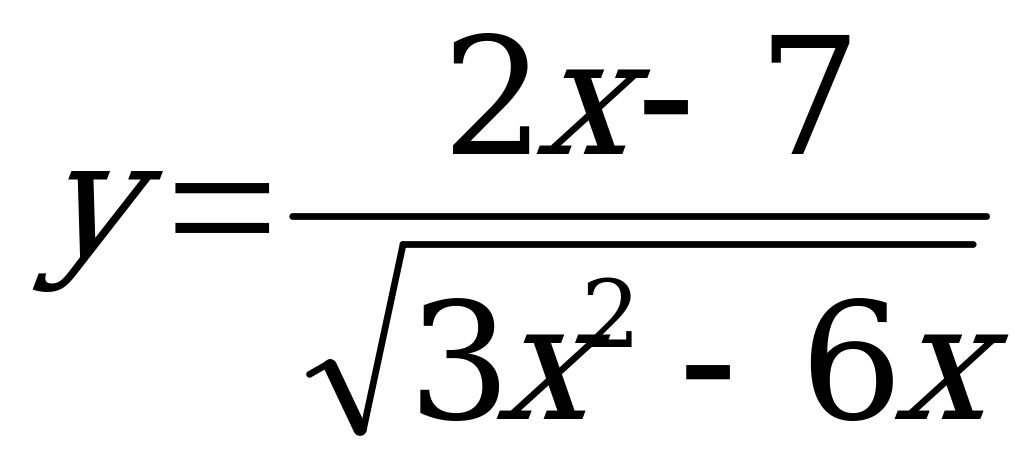
№ 4. Найдите обратную функцию:
А)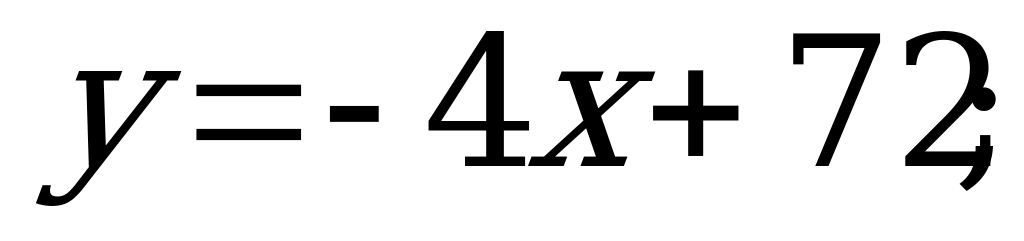 б)
б) 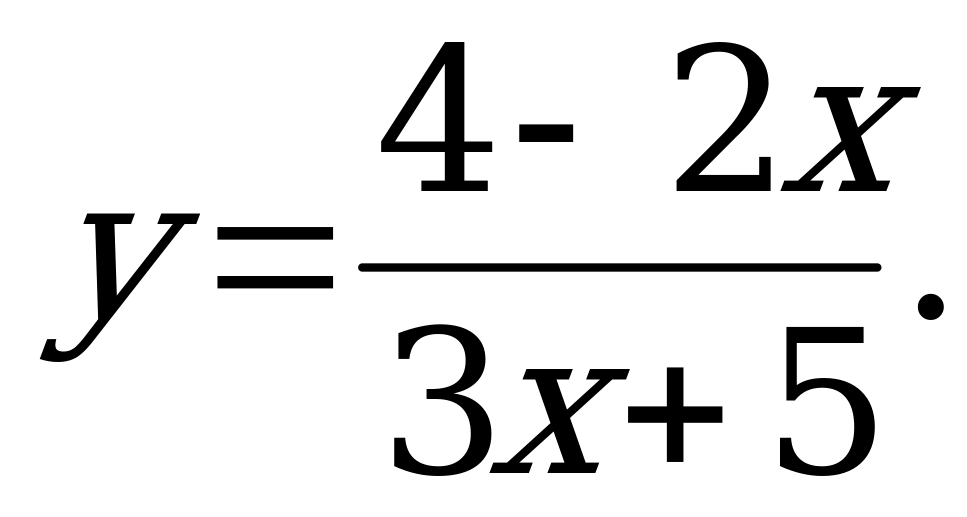
№ 5. Выполните действия над функциями: 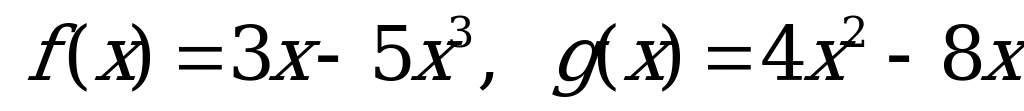
А)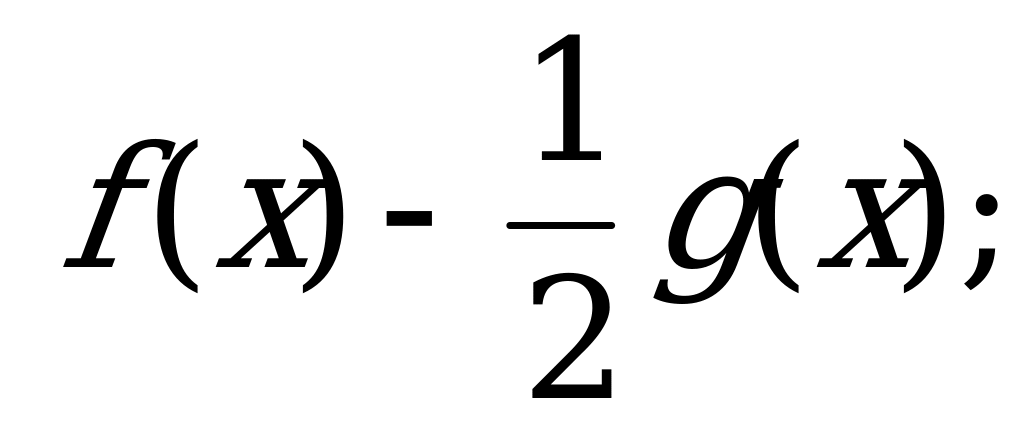 б)
б) 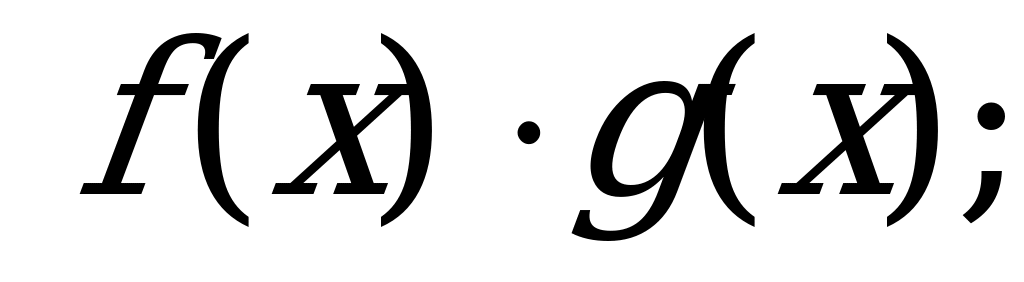 в)
в) 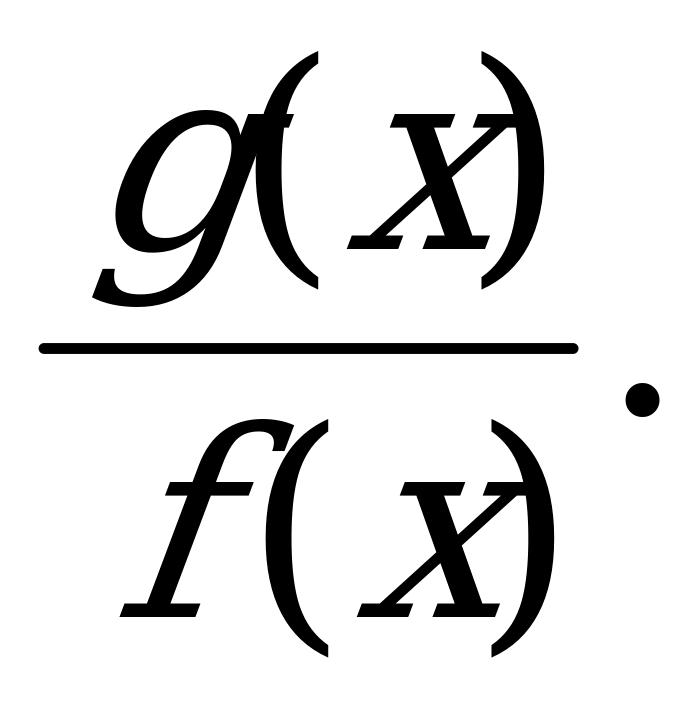
№ 6. Найдется ли такое натуральное число n, при котором график функции 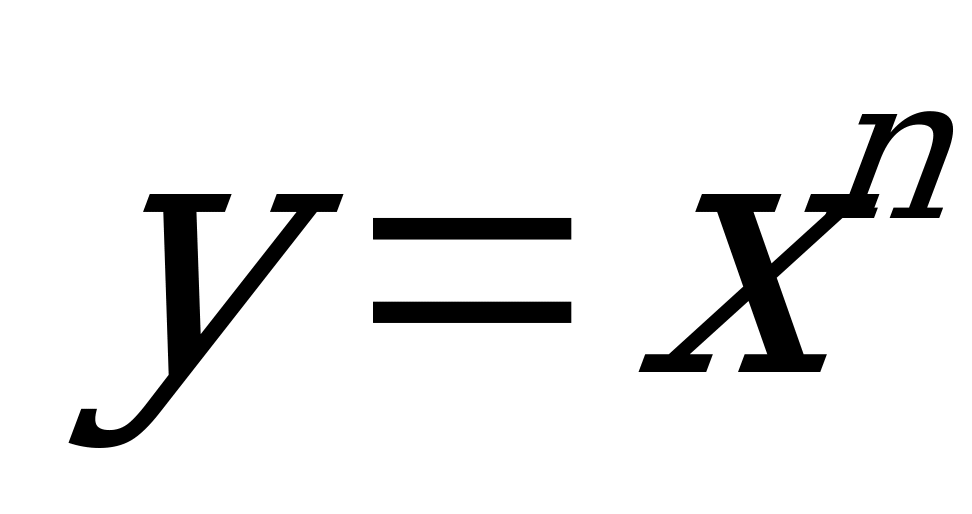 проходит через точку А(2; 6)?
проходит через точку А(2; 6)?
№ 7 Функция f(x) возрастающая, сравните:
А)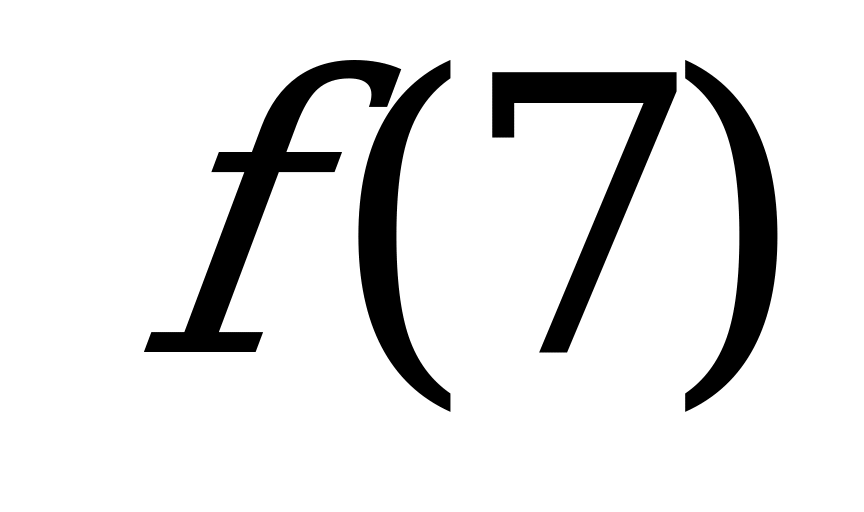 и
и 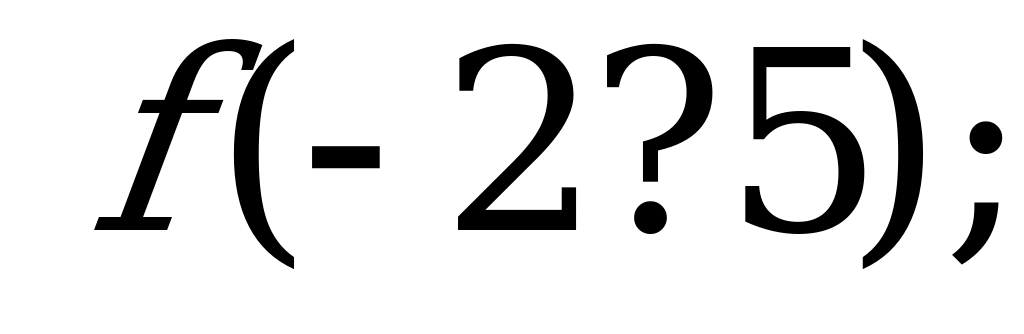 б)
б) 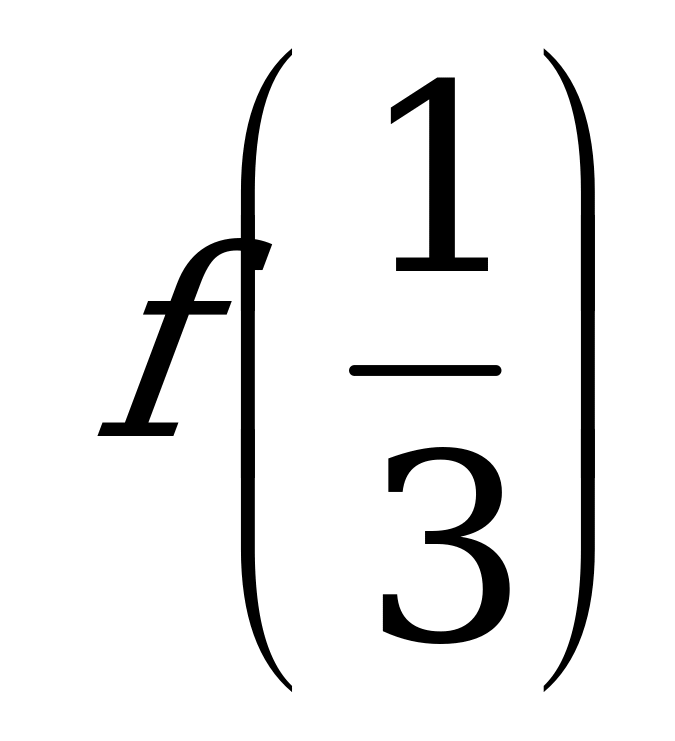 и
и 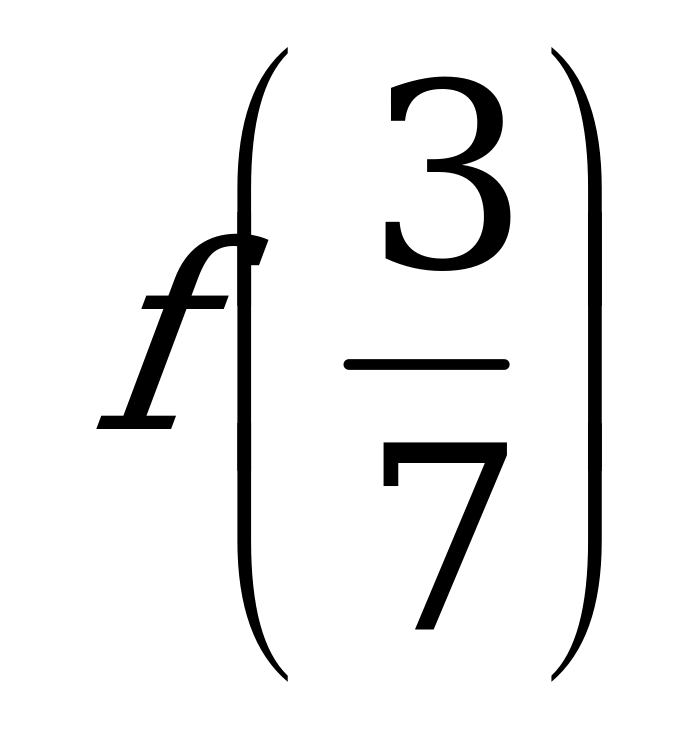
№ 8 Построить график функции с помощью элементарных преобразований: