Горбунов Василий Валентинович,
учитель математики
МБОУ «Чувашскомайнская ООШ»
Практические вопросы в области подготовки к этапам всероссийских и республиканских олимпиад школьников по математике
Организация и подготовка школьников к олимпиаде по математике преследует следующие цели:
выявление самых умных, сообразительных и одаренных учеников;
развитие творческих способностей и нестандартного мышления;
повышение интереса к углубленному изучению предмета;
создание условий поддержки и поощрения одаренных детей;
популяризация математики среди учеников школ.
Краткое описание содержания.
При подготовке к олимпиадам по математике можно выделить несколько основных направлений, которые и рассматриваются в данном методическом проекте. Выделим эти направления:
Работа учителя математики на уроке;
Внеклассная работа по математике;
Внешкольная работа по математике;
Заочная работа.
Умение решать задачи, особенно олимпиадные, всегда являлось одним из показателей математической одаренности ученика. Причем главная ценность самих олимпиад состоит не в выявлении победителей и награждении особо одаренных учащихся, а в общем подъеме предметной культуры, интеллектуального уровня учащихся.
И для того чтобы этот подъем культуры и интеллекта действительно произошел, к математическим олимпиадам учащихся надо готовить.
Тем более что сегодня часто по итогам олимпиад оценивают итоги внеклассной и внешкольной работы по предметам в школе, районе, регионе. Школьные, районные, региональные олимпиады по предметам, наряду с результатами ГИА, позволяют сравнивать качество подготовки, оценивать состояние преподавания предметов в отдельных классах школы, в отдельных школах района. Также сегодня во многом результаты работы учителя определяются и тем, каких и сколько учащихся – призеров различного рода олимпиад он подготовил.
Между тем природа может распорядиться так, что в данном месте не окажется одаренных детей, и что бы учитель ни предпринимал, все может быть безрезультатно.
С другой стороны, учитель может не предпринимать никаких особых усилий, а ученик блистает на различных соревнованиях, и прежде всего на олимпиадах различного уровня. Он добивается этого благодаря своим особым способностям, которые он продолжает развивать, работая с дополнительной литературой самостоятельно, занимаясь на всевозможных курсах, в школах при вузах, если, конечно, он учится в большом городе. Совсем другое дело, если ученик учится в сельской школе, здесь роль учителя велика. Хотя школа сегодня уже не является единственным, монопольным источником информации, знаний, умственного развития учащихся. В частности, большой вклад в образование учащихся вносит система дополнительного образования детей, много материалов и занятий предоставляют интернет технологии. Иногда еще получается так, что вроде ученик способный, у него что-то и получается решать, но у него нет никакого желания участвовать в этих олимпиадах, даже в школьных. В данном случае добиться высоких результатов практически невозможно.
Так как мы последние в два года неплохо выступили в республиканской олимпиаде по математике, данный методический проект посвящен подготовке учащихся к математическим олимпиадам.
Так как наибольших успехов в олимпиадах добиваются дети с нестандартным, творческим мышлением, высокими математическими способностями, повышенной обучаемостью математике, то одним из путей подготовки учащихся к олимпиадам является развитие их математических способностей, мышления, интеллекта. Давно известно, что люди, систематически занимающиеся умственным трудом, имеют более высокий показатель интеллекта.
Рассмотрим основные направления подготовки учащихся к математическим олимпиадам:
Работа учителя математики на уроке;
Внеклассная работа по математике;
Внешкольная работа по математике;
Заочная работа.
I. РАБОТА УЧИТЕЛЯ МАТЕМАТИКИ НА УРОКЕ
Совершенно не правы те учителя, которые при проведении уроков не уделяют должного внимания подготовке учащихся к олимпиадам. На уроке всегда можно найти место задачам, развивающим ученика. Разумеется, должен быть индивидуальный подход, в классе много учеников, которые в этих задачах ничего не понимают, а сильные ученики в этих задачах разбираются. Рассмотрим, как можно организовать работу с олимпиадными задачами по математике на уроке.
Решение олимпиадных задач, тесно связанных с темой урока.
Здесь можно решать задачи, использующие программный материал, но повышенной трудности (арифметические задачи, алгебраические и геометрические задачи). Например:
Вычислите: а) 90+89+88+…+1+0-1-2-…-90-91-92-93;
б) 1-2+3-4+5-6+…+2012-2013.
Обе приведенные задачи являются стандартными, но, если выполнять действия по порядку, не применяя законов сложения и вычитания, на это потребуется много времени. А время на олимпиадах очень ценно. Поэтому ученик, нашедший более быстрое решение этих и подобных заданий, сэкономит время на решение других задач. На уроке данные задачи можно предложить при изучении темы «Сложение и вычитани
е положительных и отрицательных чисел».
При изучении темы «Степень с натуральным показателем» можно предложить для решения учащимися следующие типы задач.
а) Сравните: 6523 и 25517.
б) На какую цифру оканчивается число 20072014?
Решение.
а) 6523 6423= (26)23 = 2138. А 25517 17=(28)17= 2136.
Так как 6523 2138, 2138 2136, a 213625517, то 6523 25517.
б) Так как последняя цифра числа 20072014 определяется последней цифрой числа 72014, то найдем значения степеней 71=7, 72=49, 73=343, 74=2401, 75=16807 и т.д. и заметим закономерность: последней цифрой являются 7, 9, 3, 1, а далее они повторяются. Так как 2014=503х4+2, то 72014 оканчивается той же цифрой, что и 72, то есть цифрой 9. Тогда и число 20072014 оканчивается на цифру 9.
Так как решение подобного рода задач требует применения определенных качеств и приемов мышления, то на уроке необходимо уделять внимание и развитию как некоторых качеств ума (прежде всего, гибкости и глубины), так и приемов умственной деятельности ( в первую очередь анализа, так как он чаще всего применятся в олимпиадных задачах, особенно геометрических).
Развитие качеств ума и приемов умственной деятельности.
Для развития гибкости ума на уроке используются такие методы:
— применение упражнения, в которых встречаются взаимно обратные операции;
— предлагаются решение задач несколькими способами, доказательства теорем различными методами;
— развивается переключение с прямого хода мыслей на обратный.
Рассмотрим примеры задач, способствующих развитию данного качества.
У двух зрячих один брат слепой, но у слепого нет зрячих братьев. Как это может быть? (Из первой фразы как будто следует, что речь в задаче идет о братьях, тогда как на самом деле зрячими оказываются сестры).
Два ученика подошли одновременно к реке. У берега реки стояла лодка (лишь для одного человека). Тем не менее оба сумели переправиться через реку в одной лодке. Каким образом? (Из первой фразы как будто кажется, что ученики подошли к реке на одном берегу, но для решения задачи получается, что они подошли к реке на разных берегах.)
Вам дано 5 спичек. Сложите из них 2 равносторонних треугольника. А если спичек будет 6, то скольких равносторонних треугольников вы можете сложить? Первая задача решается на плоскости (тогда получаются 2 равносторонних треугольника), а вторая - в пространстве (тогда получаются 4 равносторонних треугольника).
Найдите как можно больше способов решения задач. Докажите, что треугольник, в котором медиана равна половине стороны, к которой она проведена, является прямоугольным.
Решение
Способ №1
Пусть BD – заданная медиана треугольника АВС(рис2). Имеем тогда следующие соотношения для углов:
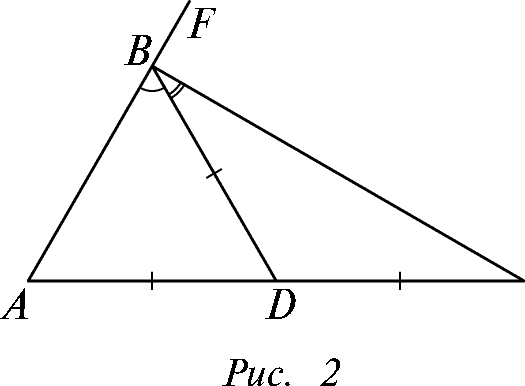
ےA + ےABD + ےDBC +ےC = 1800.
ےA = ےABD, ےC = ےDBC.
ےA + ےABD + ےDBC + ےC = 2 ےABD + 2 ےDBC = 2(ےABD + ےDBC) = = 2(ےABD + ےDBC) = 2ےABC = 1800.
ےABC = 900, а значит, треугольник АВС прямоугольный.
Вывод. При доказательстве использовались теорема о сумме углов треугольника и свойство углов при основании равнобедренного треугольника.
Способ №2.
Рассмотрим треугольник ABD. ےBDC= ےA + ےABD.
Рассмотрим треугольник DBC. ےADB = ےC + ےDBC.
В треугольнике АВD имеем ےA= ےABD.
В треугольнике DBC имеем ےD= ےDBC.
ےADB + ےBDC = 1800.
ےADB + ےBDC = ےA + ےABD + ےC + ےDBC = 2(ےABD + ےDBC)=1800. А значит ےABD + ےDBC = ےB = 900.
Вывод. В данном способе использовались теорема о внешнем угле треугольника, свойство углов при основании равнобедренного треугольника, теорема о смежных углах.
Способ №3
Пусть AF – прямая, содержащая сторону АВ(см. рис2). Имеем тогда следующие соотношения для углов:
1) ےFBC= ےA + ےC.
2) ےA= ےABD, ےC=ےDBC.
3) ےFBC = ےABD + ےDBC = ےABC.
4) ےFBC + ےABC =1800, ےFBC = ےABC, тогда ےABC = 900.
Вывод. Применялись те же рассуждения, что и во втором способе, но в других комбинациях.
Вычислите:
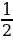 +
+ 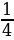 ;
; 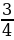 +
+ 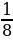 ;
; 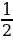 +
+ 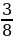 ;
; 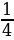 ˑ
ˑ 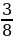 .
.
(Первые 3 примера одного типа, а четвертый - другого. Для решения четвертого примера необходимо перестроить умственную деятельность.)
Для развития глубины мышления предлагаются следующие задания:
— выделять главное и второстепенное в задаче;
— выделять существенные признаки понятия;
— вычленять ведущие закономерные отношения явлений;
— отделять главное от второстепенного.
Рассмотрим примеры задач, способствующих развитию данного качества.
Известно, что сложению соответствует одно обратное действие – вычитание; аналогично для умножения обратным действием является деление. Почему же действие возведение в степень имеет два себе обратных: извлечение корня и логарифмирование? (Для возведения числа в степень переместительный закон не действует, в отличие от сложения и умножения).
Является ли последовательность вида 3,3,3,… арифметической прогрессией? А геометрической?
Подчеркните наиболее общее понятие: медиана, отрезок, хорда, средняя линия треугольника.
Выделите основное соотношение в задаче: «Два поезда выехали одновременно навстречу друг другу из двух городов, расстояние между которыми 660 км. Через 4 часа они встретились. Найдите скорость каждого поезда, если скорость одного на 15 км/ч больше скорости другого».
Выделите существенные признаки понятий «равнобедренный треугольник», «ромб».
Иногда одна и та же задача может развивать различные качества ума. Например:
Вася живет на 5-м этаже 12-этажного дома. Он решил покататься на лифте. Сначала он поднялся на 2 этажа, потом опустился на 4 этажа, потом поднялся на 6 этажей, потом опустился на 10 этажей, потом вновь поднялся на 3 этажа. На каком этаже в итоге оказался Вася? (Развитие осознанности и гибкости ума.)
Решение. 5+2-4+6-10+3=2, но в процессе решения получалось 5+2-4+6-10= -1. Так как в процессе решения получалось -1, то в задаче есть противоречивые данные. Но, если под -1-м этажом дома понимать подвал, то все получается. Ведь лифт может опускаться иногда и в подвал!
Катеты прямоугольного треугольника равны 3 см и 4 см, а высота, проведенная к гипотенузе, равна 2 см. Чему равна гипотенуза треугольника? (Развитие осознанности и глубины ума.)
Решение. Известно, что S = 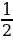 ˑ 3 ˑ 4 = 6 (см2). Но S =
ˑ 3 ˑ 4 = 6 (см2). Но S = 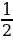 ˑ 2 ˑ c, поэтому с = 6 (см). Однако по теореме Пифагора с =
ˑ 2 ˑ c, поэтому с = 6 (см). Однако по теореме Пифагора с = 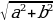 = 5 (см). Это задача с противоречивыми данными в условии. Противоречие можно получить и другим способом, найдя длины отрезков, на которые основание высоты разбивает гипотенузу.
= 5 (см). Это задача с противоречивыми данными в условии. Противоречие можно получить и другим способом, найдя длины отрезков, на которые основание высоты разбивает гипотенузу.
Рассмотренные качества ума: гибкость, глубина и другие – являются основными составляющими такой интеллектуальной особенности, как обучаемость учащихся математике, которую можно развивать как на уроке, так и вне урока.
Следует отметить, для повышения уровня обучаемости подростков необходима длительная и кропотливая ежедневная работа учителя. В 5–6-х классах нужно уделять время на уроке работе с бумагой, делая акцент на дальнейшее систематическое развитие умений, связанных с работой мелкой моторики рук. В качестве заданий могут использоваться такие методы обучения, как изготовление моделей и разверток многогранников. Так как на обучаемость влияют мотивы обучения, а в 5–6-х классах одним из основных мотивов ребенка является интерес, поэтому на уроке математики постоянно проводятся различные игры, задаются занимательные задания. При этом учитель всегда должен помнить, что детям учиться интересно только в том случае, если при изучении нового материала 50 % информации учащимся известно, а 50 % — нет.
Целесообразно предлагать задачи, рассчитанные на преодоление у учащихся психологической инертности. Например: известно, что бумеранг можно бросить так, что он вернется обратно. А можно ли как-то ухитриться и бросить теннисный мяч так, чтобы он вернулся обратно? Решение. В задаче незримо присутствует ограниче-ние сферы поиска решения: бумеранг бросают под углом к горизонту. Поэтому учащиеся отвечают: бросить против ветра; бросить в стену; «подкрутить» мяч, как в футболе. И очень немногие догадаются: мяч надо бросить вверх — и он вернется обратно. Но если эту задачу предложить решить без упоминания бумеранга, то большинство детей даст правильный ответ. Данный тип задач является для учащихся наиболее сложным. Плюсом подобного рода заданий является то, что такие задачи учат поиску нестандартных решений, альтернативных вариантов решений.
Итак, переходим к другим направлениям работы учителя математики с целью лучшей подготовки учащихся к математическим олимпиадам.
II. ВНЕКЛАССНАЯ РАБОТА ПО МАТЕМАТИКЕ.
Под внеклассной работой по математике понимаются необязательные систематические занятия учащихся с преподавателем во внеурочное время.
В теории и методике обучения математике различают два типа внеклассной работы.
К первому типу относится внеклассная работа с учащимися, отстающими от других в изучении программного материала (дополнительные занятия после уроков). Основной целью ее является своевременная ликвидация (и предупреждение) имеющихся у учащихся пробелов в знаниях и умениях по курсу математики.
Вторым типом внеклассной работы является работа с учащимися, проявляющими к изучению математики повышенной по сравнению с другими интерес и способности. Последний тип и является собственно внеклассной работой в традиционном понимании этого слова.
Как раз этот тип и будет применяться как для подготовки, так и для проведения математических олимпиад.
Наиболее важными задачами внеклассной работы на современном этапе развития школы являются следующие:
пробуждение и развитие устойчивого интереса учащихся к математике и ее приложениям;
расширение и углубление знаний учащихся по программному материалу;
развитие математических способностей и мышления у учащихся;
развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой;
расширение и углубление представлений учащихся о практическом значении математики в технике экономике;
расширение и углубление представлений учащихся о культурно-исторической ценности математики, о роли ведущих ученых математиков в развитии мировой науки;
осуществление индивидуализации и дифференциации;
разностороннее развитие личности.
Внеклассная работа может осуществляться в самых разнообразных видах и формах. Условно можно выделить три основных вида внеклассной работы.
Индивидуальная работа – работа с учащимися с целью руководства внеклассным чтением по математике, подготовкой докладов, рефератов, математических сочинений, изготовлением моделей; работа с консультантами; подготовка некоторых учащихся к участию районной или республиканской олимпиаде.
Групповая работа – систематическая работа, проводимая с достаточно постоянным коллективом учащихся. К ней можно отнести факультативы, кружки, спец-курсы, элективные курсы.
Массовая работа – эпизодическая работа, проводимая с большим детским коллективом. К данному виду относятся вечера, научно-практические конференции, недели математики, олимпиады, конкурсы, соревнования и т. п.
На практике все три вида внеклассной работы тесно связаны друг с другом.
Кружки (факультативы, спецкурсы) являются основной формой работы с наиболее способными учащимися по математике. Только здесь можно рассмотреть олимпиадные задачи, решаемые специальными методами. Так как у нас в республике олимпиады проводятся с 4 класса, то кружки можно организовать уже в младших классах, если есть способные дети.
В частности, в 5-6 классах можно рассмотреть различные типы логических задач, задачи на применение некоторых инвариантов, математические ребусы, задачи на разрезание, геометрические упражнения со спичками и др., в 7-8 классах – принцип Дирихле, игры, графы, решение более сложных логических задач, а в 9-11 классах – решение уравнений в целых числах, нестандартных уравнений.
Также некоторые занятия кружка можно посвятить и развитию каких-то определенных качеств ума, приемов умственной деятельности, подобрав специальные упражнения, организовав эти занятия в виде практикумов, тренингов и т.п. Хорошо, когда способных детей несколько ( в больших школах это возможно), между ними можно проводить математические соревнования и различные игры. Они необходимы как для текущего контроля степени усвоения рассмотренного материала, так и для психологической подготовки к будущим олимпиадам. В 8 -9 классах можно совместить подготовку к ОГЭ с подготовкой к олимпиадам. Задачи 2 части, тем более по геометрии, можно использовать при подготовке к олимпиадам. Приведу план индивидуальных занятий.
План подготовки к олимпиаде по математике
обучаемый: ………., 9 класс
| № | Тема |
| Период |
| 1 | Вводное занятие. Основные правила при решении олимпиадных задач. Подготовка к школьной олимпиаде. Разбор прошлогодних заданий | 4 | сентябрь |
| 2 3 | Целые числа. Участие в школьной олимпиаде Разбор заданий школьной олимпиады | 1 4 | Сентябрь октябрь |
| 4 | Четность. | 1 | Октябрь |
| 5 6 | Признаки делимости. Подготовка к районной олимпиаде. Разбор прошлогодних заданий. | 2 3 | Октябрь Октябрь |
| 7
8 | Текстовые задачи (движение, совместная работа, проценты, смеси и сплавы и другие) Участие в районной олимпиаде Разбор заданий прошлогодней районной олимпиады | 2
4 | Ноябрь Ноябрь или декабрь |
| 9 10 | Сюжетно - бытовые задачи. Подготовка к республиканской олимпиаде( в случае приглашения) | 2 4 | Декабрь
|
| 11 | Разбор заданий республиканской олимпиады. Инварианты. Геометрические задачи | 5 | Январь |
| 12 | Принцип Дирихле. Участие в республиканской олимпиаде(в случае приглашения) Разбор заданий республиканской олимпиады. | 5
| Февраль |
| 13 | Задачи, решаемые с конца. Круги Эйлера. | 1 | Февраль |
| 14 | Задачи в сказках, рассказах, стихах. | 2 | Март |
| 15 | Логические задачи. Комбинаторика. Числовые ребусы. | 3 | Март |
| 16 | Диофантовы уравнения. | 1 | Апрель |
| 17 | Неравенства. | 1 | Апрель |
| 18 | Системы счисления. | 1 | Апрель |
| 19 | Популярные задачи по планиметрии (задачи на разрезание, составление, наглядная геометрия и другие) | 2 | Апрель |
| 20 | Параллельность, перпендикулярность. | 2 | Май |
учитель: Горбунов В.В. форма обучения: очно-заочная, домашняя подготовка уч-ся.
Примечание: В случае приглашения на республиканскую олимпиаду, темы, запланированные на февраль - май месяцы, нужно будет пройти в декабре и январе.
III. ВНЕШКОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ
В отличие от внеклассной работы, которая проводится с учащимися одной школы учителями математики (а иногда и родителями учащихся) этой же школы, внешкольная работа организуется с учащимися нескольких школ района, города и региона. При этом внешкольные занятия с учащимися могут организовываться как на базе какой-то школы, так и на базе образовательно-оздоровительных лагерей. У нас в районе, например, на базе Мокрокурналинской средней школы в прошлые года были организованы занятия по математике с выпускниками, занятия в лагере «Фэнсар». А в республике при лагере «Дуслык» организовываются смены по предметам, где как раз и разбираются олимпиадные задания. К сожалению, смены эти платные, не все желающие ученики могут туда попасть.
Внешкольная работа, прежде всего, предназначена для учащихся, уже увлеченных математикой.
Основными целями организации внешкольной работы являются:
развитие мышления и математических способностей учащихся;
углубление знаний учащихся по математике.
Проводят внешкольную работу, как правило, преподаватели и студенты вузов, работники центров дополнительного образования, а также и учителя некоторых школ.
Задача учителя математики будет состоять в том, чтобы учащиеся классов, в которых он ведет математику, смогли участвовать в таких видах внешкольной деятельности, которые им нужны. Главное – владеть информацией обо всех формах внешкольной работы, в которой могут принимать участие его ученики. Не каждый учитель может обладать такими качествами, которые позволят ему подготовить призера региональной или всероссийской олимпиады, каждый имеет свой «потолок» в интеллектуальном развитии. Иногда без привлечения других специалистов добиться продвижения ученика будет невозможно.
IV. ЗАОЧНАЯ РАБОТА
Одним из направлений для подготовки к олимпиадам является и заочная работа в различных школах при вузах. Уровень предлагаемых там заданий очень высок, большинство идей в этих заданиях встречается на различного уровня олимпиадах. И выполнение такого рода заданий будет способствовать, конечно же, подготовке учащихся к олимпиадам. Во многих крупных городах имеются школы одаренных детей, в вузах – факультеты (отделения, центры) довузовской подготовки. В них можно обучаться и заочно. Задача учителя математики будет заключаться в том, чтобы донести информацию о них до своих учеников, убедить некоторых из них в необходимости заочного обучения в данных школах, на данных факультетах. Конечно, возникают трудности, если ученик учится в сельской школе и на большом расстоянии от крупных городов. Если посмотреть на результаты республиканских и всероссийских олимпиад, мы видим, что в основном победителями и призерами становятся ученики именно крупных городов. Разумеется, это все зависит от подготовки к этим олимпиадам.
Но все-таки некоторые вузы, такие как КФУ, КНИТУ(КАИ) и др., ведут работу по отбору талантливых детей по всей республике. В современное время это возможно благодаря интернету. Они проводят сначала заочные по интернету олимпиады, а потом по результатам заочных туров приглашают на очный тур.
Да и вообще в самом интернете проводятся множество всяких олимпиад, как платных, так и бесплатных, можно найти много материалов для подготовки к олимпиадам. Например:
Таким образом, только задействовав все эти четыре направления в подготовке учащихся к олимпиадам (хотя это не главное в жизни, куда важнее интеллектуальное развитие ученика, подготовка его к современной жизни, где без острой конкуренции уже не обойтись), можно ожидать успеха.
Литература
А.В. Фарков. Математические олимпиады: методика подготовки.
Аспекты и тенденции педагогической науки. Материалы международной научной конференции.
Интернет – ресурсы








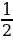 +
+ 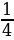 ;
; 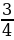 +
+ 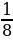 ;
; 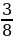 ;
; 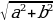 = 5 (см). Это задача с противоречивыми данными в условии. Противоречие можно получить и другим способом, найдя длины отрезков, на которые основание высоты разбивает гипотенузу.
= 5 (см). Это задача с противоречивыми данными в условии. Противоречие можно получить и другим способом, найдя длины отрезков, на которые основание высоты разбивает гипотенузу.









