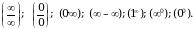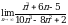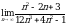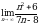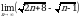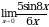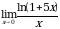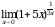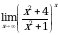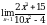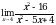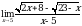Комплект контрольно-оценочных средств разработан на основе
Федерального государственного образовательного стандарта по специальности
среднего профессионального образования 23.02.07 Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей, утвержденного приказом Министерства образования и науки от 9 декабря 2016 года № 1547 (зарегистрирован Министерством юстиции Российской Федерации 26 декабря 2016г., регистрационный №44936)
Просмотр содержимого документа
«Практическое занятие №2 Тема: «Нахождение пределов функций с помощью замечательных пределов» (комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ЕН.01 МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СПО 23.02.07 ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ ДВИГАТЕЛЕЙ, СИСТЕМ И АГРЕГАТОВ АВТОМОБИЛЕЙ)»
Практическое занятие №2
Тема: «Нахождение пределов функций с помощью замечательных пределов»
Цель: сформировать умение находить пределы последовательностей и пределы функций, использовать замечательные пределы для нахождения пределов.
Теоретические сведения к практической работе
Пусть существует последовательность действительных чисел 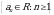 .
.
Число а называется пределом последовательности
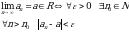
Число А называют пределом функции f(x) при 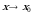 (и пишут
(и пишут 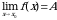 ), если для любого
), если для любого 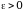 найдется число
найдется число 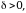 такое, что для всех
такое, что для всех 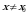 , удовлетворяющих условию
, удовлетворяющих условию 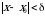 , выполняется неравенство
, выполняется неравенство 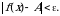
Теоремы о пределах:
1. 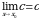 (c=const).
(c=const).
2. Если 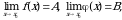 то:
то:
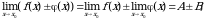
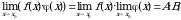
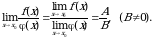
Первый замечательный предел: 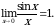
Второй замечательный предел (число е = 2,718…):
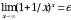 или
или 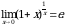
Замечательные пределы:
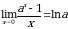
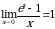
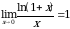
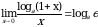
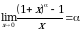
Чтобы найти предел элементарной функции 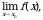 нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х=х0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х=х0. При вычислении пределов полезно использовать следующие соотношения. Если
нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х=х0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х=х0. При вычислении пределов полезно использовать следующие соотношения. Если 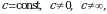 то, учитывая свойства б.б. и б.м. функций, получим:
то, учитывая свойства б.б. и б.м. функций, получим:
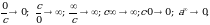 если
если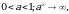 если a1.
если a1.
Случаи, в которых подстановка предельного значения аргумента
в функцию не дает значения предела, называют неопределенностями;
к ним относятся неопределенности видов:
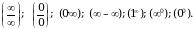
Содержание практической работы
Задание 1. Вычислить пределы последовательностей:
1. 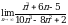
2. 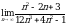
3. 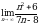
4. 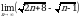
Задание 2. Вычислить пределы функций, используя замечательные пределы:
1. 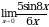
2. 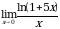
3. 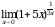
4. 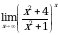
Задание 3. Вычислить пределы функций:
1. 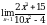
2. 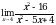
3. 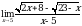







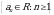 .
. 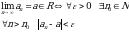
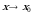 (и пишут
(и пишут 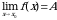 ), если для любого
), если для любого 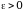 найдется число
найдется число 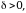 такое, что для всех
такое, что для всех 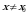 , удовлетворяющих условию
, удовлетворяющих условию 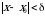 , выполняется неравенство
, выполняется неравенство 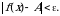
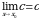 (c=const).
(c=const).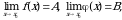 то:
то: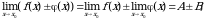
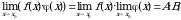
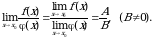
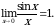
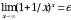 или
или 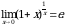
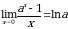
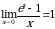
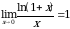
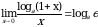
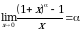
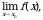 нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х=х0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х=х0. При вычислении пределов полезно использовать следующие соотношения. Если
нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х=х0 принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х=х0. При вычислении пределов полезно использовать следующие соотношения. Если 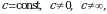 то, учитывая свойства б.б. и б.м. функций, получим:
то, учитывая свойства б.б. и б.м. функций, получим: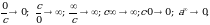 если
если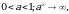 если a1.
если a1.