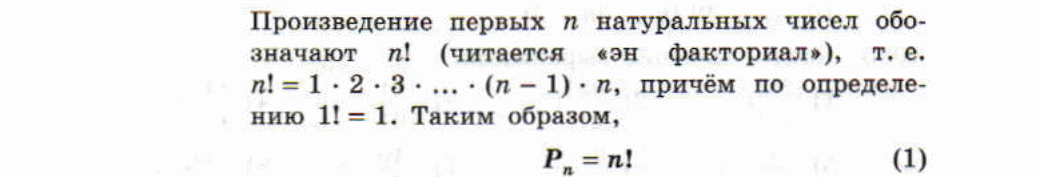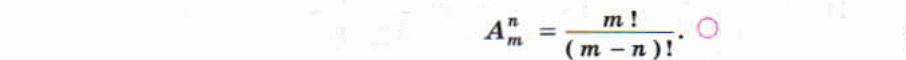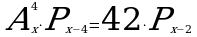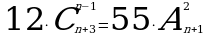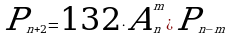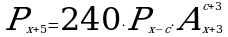Практическое занятие №43 Тема: «Основные понятия комбинаторики» (комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ОД.03МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ 09.02.06СЕТЕВОЕ И СИСТЕМНОЕ АДМИНИСТРИРОВАНИЕ)

Практическое занятие №43

Тема: «Основные понятия комбинаторики»

Цель: отработать умение решать задачи на расчет выборок (перестановок, размещений, сочетаний) с применением элементов и формул комбинаторики, развивать самостоятельную мыслительную деятельность, а также вычислительные навыки и творческое мышление студентов.

Теоретические сведения к практической работе

П ЕРЕСТАНОВКИ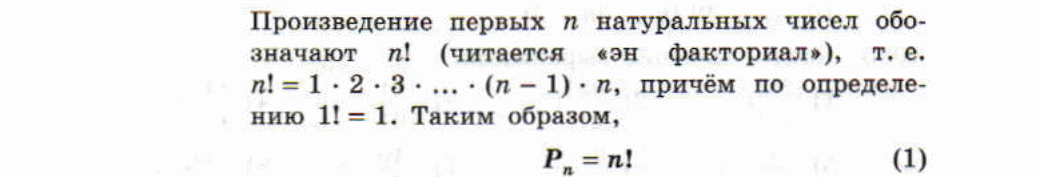

РАЗМЕЩЕНИЯ

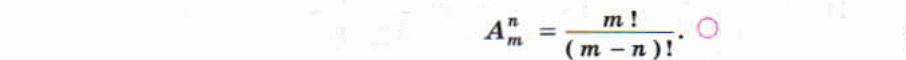
СОЧЕТАНИЯ

Задания для практической работы

1 вариант.

1. Решите уравнение: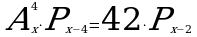

2. Сколькими способами могут разместиться пять человек вокруг круглого стола?

3. Сколько двузначных чисел можно составить из цифр 1;2;5;8;9 так чтобы в каждом числе не было одинаковых цифр?

4. В бригаде из двадцати пяти человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

5. В вазе с фруктами лежит 12 персиков и 9 слив. Сколькими способами можно выбрать 4 персика и 3 сливы?

2 вариант.

1. Решите уравнение: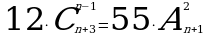

2. Сколькими способами можно расставить на полке семь книг?

3. Сколько существует вариантов распределения трех призовых мест, если в розыгрыше участвуют семь команд?

4. Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?

5. На полке стоит 4 энциклопедии и 11 детективов. Сколькими способами можно выбрать пять детективов и две энциклопедии?

3 вариант.

1. Решите уравнение: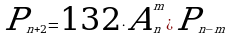

2. Сколькими способами можно составить список из шести человек?

3. Сколько различных четырехзначных чисел можно составить из цифр 1;2;3;4;5;6;7;8;9?

4. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

5. В классе учатся 16 мальчиков и 12 девочек. Для генеральной уборки класса требуется выделить 4 мальчиков и 3 девочек. Сколькими способами это можно сделать?

4 вариант.

1. Решите уравнение: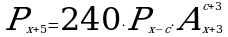

2. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно?

3. Сколько вариантов расписания можно составить на один день, если всего имеется восемь учебных предметов, а в расписание на день могут быть включены только три из них?

4. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?

5. В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала?