Практическое занятие №44 Тема: «Относительная частота события, свойство её устойчивости» (комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ОД.03МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ 09.02.06СЕТЕВОЕ И СИСТЕМНОЕ АДМИНИСТРИРОВАНИЕ)

Практическое занятие №44

Тема: «Относительная частота события, свойство её устойчивости»

Цель: закрепить понятие относительной частоты события, понимание свойства устойчивости относительной частоты события, отработать умение решать задачи на расчет относительной частоты события, развивать самостоятельную мыслительную деятельность, а также вычислительные навыки и творческое мышление студентов.

Теоретические сведения:

Относительной частотой события  называют отношение числа испытаний 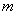 , в которых данное событие появилось, к общему числу  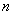 фактически проведённых испытаний:
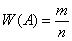, или короче: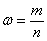 

Относительная частота наряду с вероятностью является одним из ключевых понятий ТВ и МС, но если классическое либо геометрическое определение вероятности не требуют проведения испытаний, то относительная частота рассчитывается исключительно ПОСЛЕ опытов на основе фактически полученных данных.

В том случае, если серии испытаний проводятся в неизменных условиях, то относительная частота обнаруживает свойство устойчивости, то есть колеблется около определённого значения.

Пусть некий профессиональный стрелок произвёл 100 выстрелов по мишени и попал 83 раза.

Тогда относительная частота поражения цели составит:  .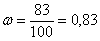

Предположим, что тот же самый стрелок в точно такой же «форме» и в приблизительно таких же условиях снова провёл серию из 100 выстрелов. Вероятно ли, что он снова попадёт 83 раза? Не очень. Но количество попаданий вряд ли будет сильно отличаться от предыдущего результата. Пусть, например, стрелок попал 79 раз. Тогда относительная частота поражения цели составит:  .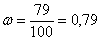

В третьей серии из 100 выстрелов, проведённой при похожих обстоятельствах, данный стрелок попал 81 раз, 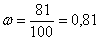  и т.д.

Иногда могут случаться блестящие серии более 90 попаданий, иногда «провалы», но среднее количество попаданий будет варьироваться около 80. И когда количество фактически проведённых испытаний станет достаточно большим, то речь зайдёт о статистической вероятности. Если в одинаковых (примерно одинаковых) условиях проведено достаточно много испытаний, то за статистическую вероятность события принимают относительную частоту данного события либо близкое число.

Предположим, что на протяжении нескольких лет наш спортсмен, сохраняя стабильный уровень подготовки, совершил 10000 выстрелов и попал 8037 раз. Относительная частота поражения цели составит: 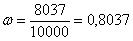  и за статистическую вероятность его результативности целесообразно принять  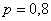, которая становится теоретической оценкой, например, перед грядущими соревнованиями.

Именно так собирается богатая спортивная статистика в различных видах спорта.

Аналогичная история с утверждением «Вероятность изготовления бракованной детали на данном станке равна 0,05». Эту оценку невозможно получить с помощью классического определения вероятности – она следует только из практики! Если на станке произведены десятки тысяч деталей и на каждую, скажем, тысячу выпущенных деталей, приходится в среднем 50 бракованных, то в качестве статистической вероятности брака принимается значения  .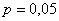

Вот, например, во многих задачах фигурирует вероятность рождения мальчика 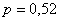 . Откуда взялось данное число? Из многолетнего подсчёта фактически рождённых детей в определённом регионе. Это вовсе не значит, что среди 100 новорожденных будет ровно 52 мальчика. В следующей сотне рождённых их может оказаться, например, 45, и относительная частота  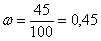 будет далека от истины. Но если рассмотреть выборку в тысячи и десятки тысяч младенцев, то  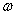 отклонится от  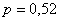 совсем-совсем незначительно. И это уже не случайность. Как известно, такое соотношение новорожденных сложилось эволюционно – по причине бОльшей смертности мужчин.

В учебном пособии В.Е. Гмурмана есть весьма удачный пример, в котором продемонстрировано, как при подбрасывании монеты относительная частота появления орла приближается к своей вероятности 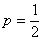  (полученной по классическому определению):

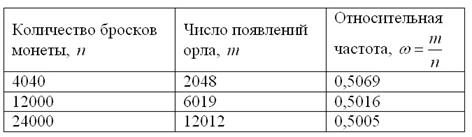
Какой можно сделать вывод? С увеличением количества независимых испытаний случайность превращается в закономерность.

Содержание практической работы:

№1 Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей. Вычислить отно­сительную частоту появления нестандартных деталей.

№2 По цели произвели 24 выстрела, причем было зареги­стрировано 19 попаданий. Вычислить относительную частоту поражения цели.

Замечание. Длительные наблюдения показали, что если в одина­ковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свой­ство состоит в том, что в различных опытах относитель­ная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого по­стоянного числа. Оказалось, что это постоянное число есть вероятность появления события. Таким образом, если опытным путем установлена от­носительная частота, то полученное число можно принять за приближенное значение вероятности.

№3 По данным шведской статистики, относительная час­тота рождения девочек за 1935 г. по месяцам характеризуется сле­дующими числами (числа расположены в порядке следования меся­цев, начиная с января): 0,486; 0,489; 0,490; 0.471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0.482; 0,473.

Найти приближенное значение относительной частоты рождения девочек за 1935 год, округлив ответ до тысячных.
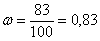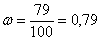