Практическое занятие №52
Тема: «Решение текстовых задач профессионального содержания»
Цель: формировать умение решать задачи с профессиональной направленностью, показывая применение математических знаний и методов в выбранной специальности.
Теоретические сведения к практической работе:
Современный уровень социально-экономического развития страны требует от системы профессионального образования ставить своей главной целью подготовку для общества квалифицированных специалистов, способных работать в опережающем, инновационном режиме, мыслить и действовать нестандартно, принимать оптимальные решения в ситуациях, выходящих за пределы имеющейся информации. Главной задачей профессионального образования становится формирование у выпускника общих и профессиональных компетенций, позволяющих ему овладеть видами деятельности, указанными в ФГОС по избранной специальности или профессии Задачами профессионально-ориентированного подхода в процессе обучения математике являются:
- показать связь математики с реальной действительностью;
- усилить практическую направленность для качественной подготовки студентов;
- формировать умение организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
Математические задачи с профессиональной направленностью должны:
1. Иметь реальное, практическое содержание, раскрывающее практическую ценность и значимость приобретенных математических знаний;
2. Отражать межпредметные связи различных дисциплин общепрофессионального и профессионального циклов на конкретных примерах с практическим содержанием;
3. Отражать производственную ситуацию, показывая применение математических знаний и методов в выбранной специальности;
4. Содержать численные данные, которые соответствуют существующим на практике;
5. Предполагать проведение приближенных вычислений, а также применение вычислительной техники.
Алгоритм решения задач с профессиональной направленностью:
1. Анализ условия задачи.
Формулировка задачи осуществляется на описательном языке. От правильной постановки задачи, указания ресурсов, которыми мы располагаем, зависит результат ее решения.
2. Построение математической модели задачи.
3. Перевод исходной задачи на математический язык: вводятся переменные, ищутся связи между ними и устанавливаются ограничения на них, которые записываются в виде уравнений, неравенств или их систем. Любая математическая задача — модель каких-то прикладных задач (экономических, физических, технических и т.п.).
4. Решение математической модели задачи. Изучается полученная модель. Составляется план решения, если есть необходимость, то целесообразно сделать рисунок. Если задача является типовой, и ее решение определяется в рамках программы учебной дисциплины, то она решается по соответствующему ей алгоритму. Если задача никогда не решалась, то ищется необходимый алгоритм.
5. Интерпретация решения.
Это перевод решения задачи на исходный профессиональный язык и конкретизация прикладного смысла ответа задачи.
Примеры задач профессиональной направленности для специальности
08.02.08 Монтаж и эксплуатация оборудования и систем газоснабжения
Пример 1. Функция g(t) описывает расход газа в зависимости от времени и задается уравнением g(t) = 2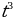 - 5
- 5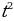 + 3t.
+ 3t.
а) Найдите производную функции g(t).
б) Найдите момент времени, когда расход газа достигает максимального значения.
Решение:
а) Для нахождения производной функции g(t), нужно взять производную каждого члена по отдельности. В данном случае, производная функции g(t) будет равна g'(t) = 6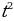 - 10t + 3.
- 10t + 3.
б) Чтобы найти момент времени, когда расход газа достигает максимального значения, нужно найти точку экстремума функции g(t). Для этого приравняем производную g'(t) к нулю и решим полученное уравнение:
6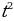 - 10t + 3 = 0.
- 10t + 3 = 0.
D = 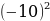 - 4*6*3 = 100 – 72 = 28 D0 t =
- 4*6*3 = 100 – 72 = 28 D0 t = 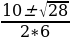 =
= 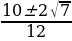 =
= 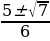
Решая это квадратное уравнение, мы найдем два значения t. Подставим эти значения в исходную функцию g(t) и найдем соответствующие значения времени, когда расход газа достигает максимального значения.
П ример 2.
ример 2. 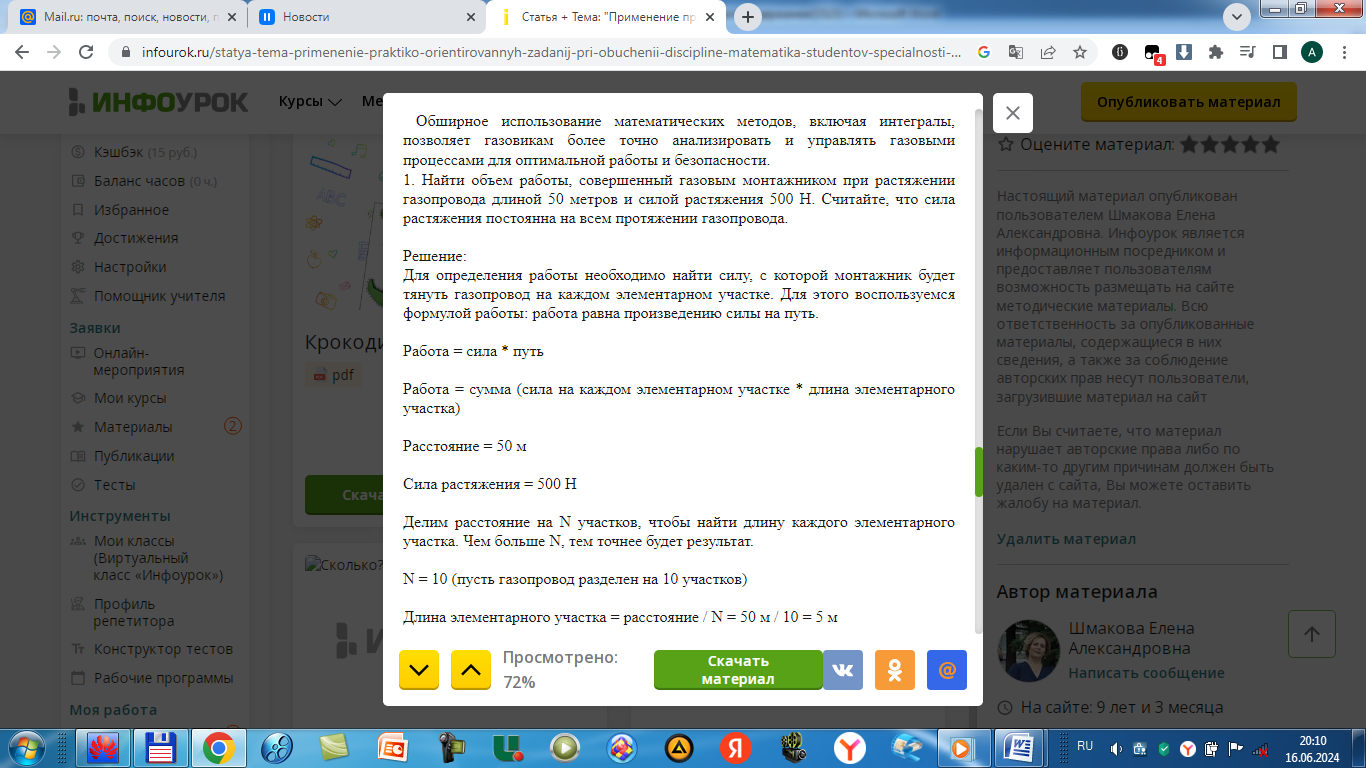
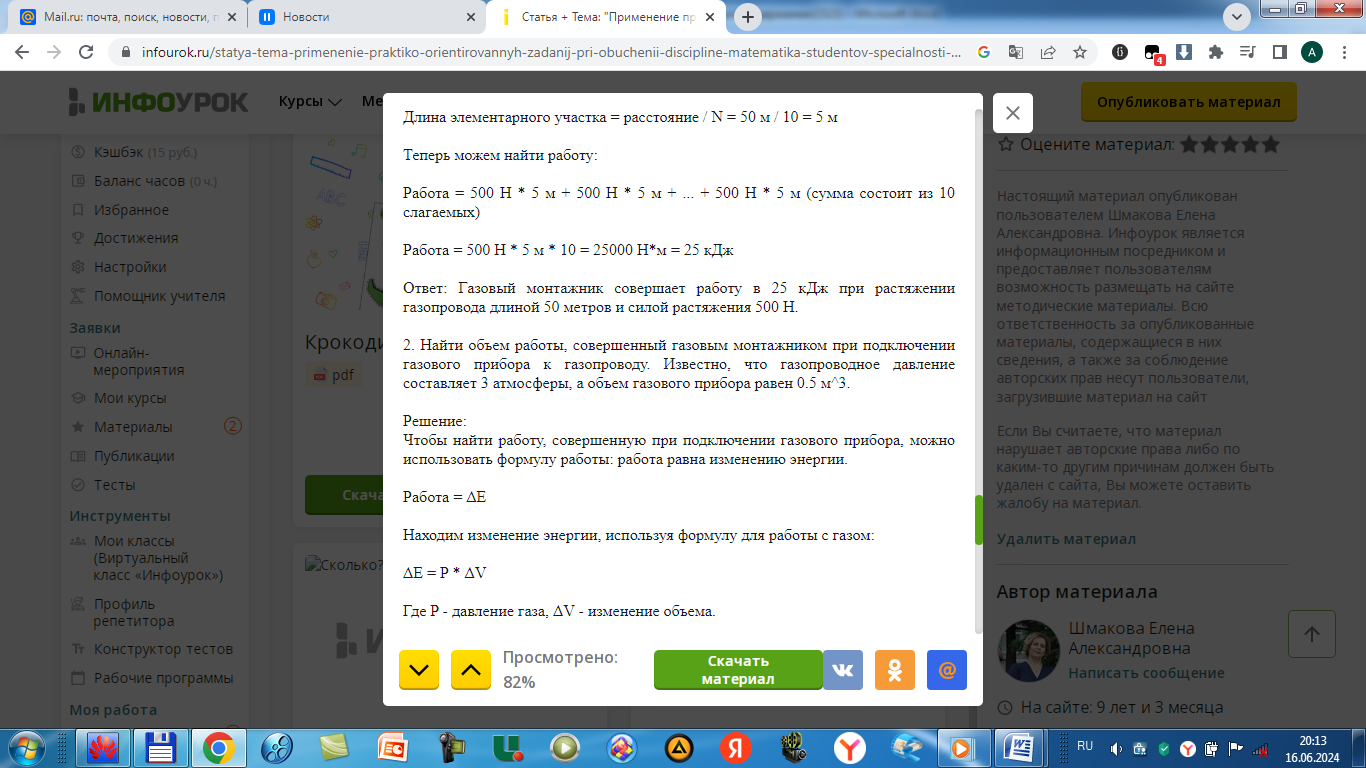
П ример 3.
ример 3. 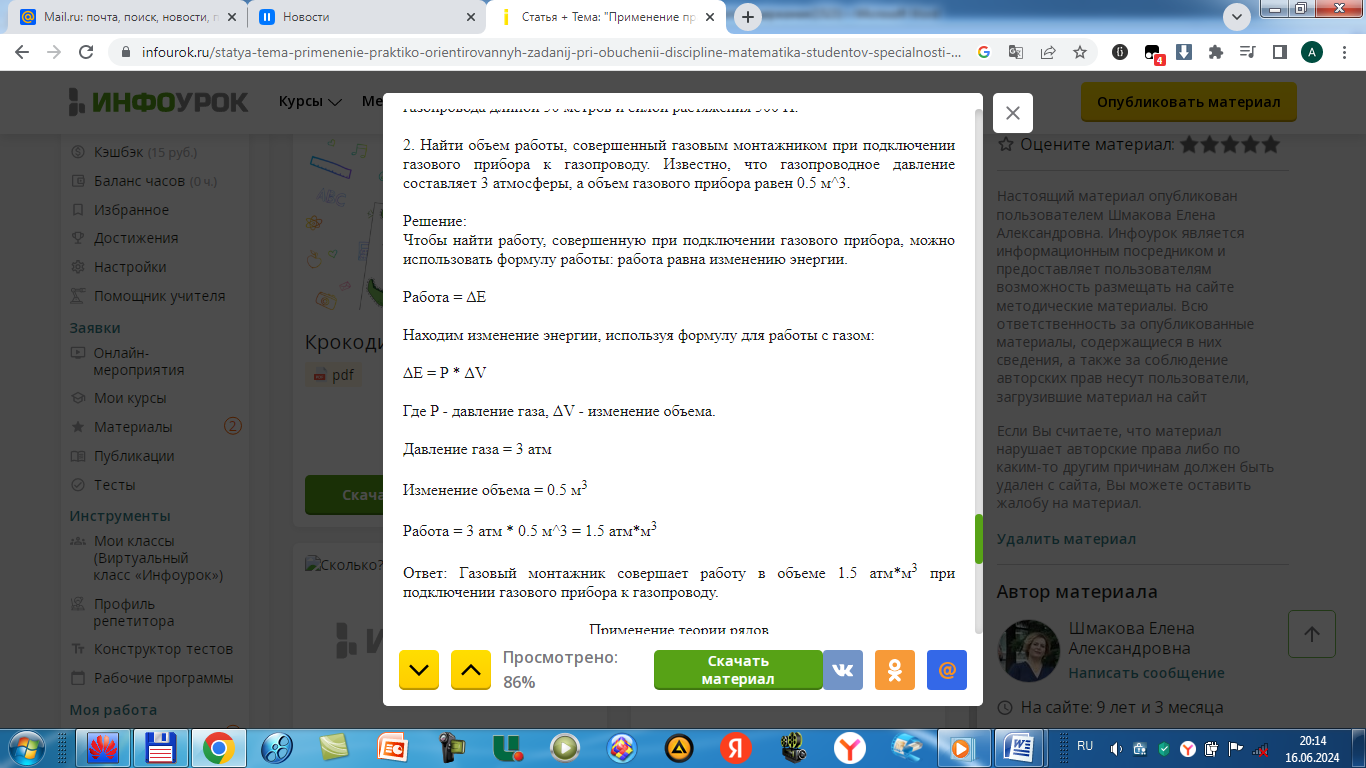
Задания для практической работы:
№1
Выполнить решение задачи из примера №1, найдя соответствующие значения времени, когда расход газа достигает максимального значения.
№2
Найти объем работы, совершенный газовым монтажником при растяжении газопровода длиной 75 метров и силой растяжения 470 Н. Считать силу растяжения постоянной на всем протяжении газопровода.
№3
Найти объем работы, совершенный газовым монтажником при подключении газового прибора к газопроводу. Известно, что газопроводное давление составляет 3,5 атмосферы, а объем газового прибора равен 0,8 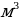 .
.







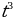 - 5
- 5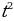 + 3t.
+ 3t.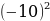 - 4*6*3 = 100 – 72 = 28 D0 t =
- 4*6*3 = 100 – 72 = 28 D0 t = 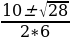 =
= 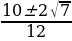 =
= 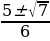
 ример 2.
ример 2. 

 ример 3.
ример 3. 
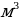 .
.









