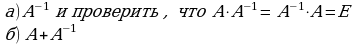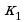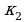Комплект контрольно-оценочных средств разработан на основе
Федерального государственного образовательного стандарта по специальности
среднего профессионального образования 23.02.07 Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей, утвержденного приказом Министерства образования и науки от 9 декабря 2016 года № 1547 (зарегистрирован Министерством юстиции Российской Федерации 26 декабря 2016г., регистрационный №44936)
Просмотр содержимого документа
«Практическое занятие №7 Тема: «Действия с матрицами. Нахождение обратной матрицы»(комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ЕН.01 МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СПО 23.02.07 ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ ДВИГАТЕЛЕЙ, СИСТЕМ И АГРЕГАТОВ АВТОМОБИЛЕЙ)»
Практическое занятие №7
Тема: «Действия с матрицами. Нахождение обратной матрицы»
Цель: проверить знание свойств определителей 2 и 3 порядков, правила вычисления определителей, вычислительные навыки, проверить умения нахождения миноров, алгебраических дополнений и определителей, правило вычисления обратной матрицы.
Теоретические сведения к практической работе
Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число 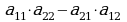 .
.
Определитель обозначают символом
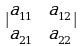
По определению,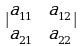 =
= 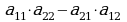 .
.
Числа а11, а12, а21, а22называются элементами определителя.
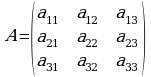 - квадратная матрица размера 3x3
- квадратная матрица размера 3x3
Cоответствующим ей определителем третьего порядка называется число, которое вычисляется следующим образом
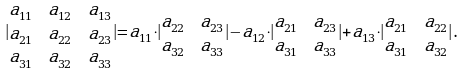
Квадратная матрица А называется вырожденной, если ее определитель равен нулю, и невырожденной, если ее определитель не равен нулю.
Если А - квадратная матрица, то обратной по отношению к А называется матрица, которая будучи умноженной, на А (как справа так и слева), дает единичную матрицу. Обозначается А-1 .
А-1 А = А А-1 = Е
Если обратная матрица А-1существует, то матрица А называется обратимой.
Операция вычисления обратной матрицы при условии, что она существует, называется обращением матрицы.
Теорема: для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица была невырожденной, то есть, чтобы ее определитель был отличен от нуля.
При условии 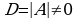 обратная матрица находится по формуле
обратная матрица находится по формуле
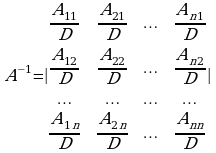
Для нахождения обратной матрицы используют следующую схему:
Находят определитель матрицы А;
Находят алгебраические дополнения Аij всех элементов матрицы А и записывают новую матрицу;
Меняют местами столбцы полученной матрицы (транспонируют матрицу);
Умножают полученную матрицу на 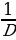
Содержание практической работы
Вариант 1 (1,3) Вариант2 (2,4).
Вычислить определители:
1) 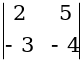 2)
2) 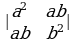 3)
3) 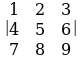 4)
4) 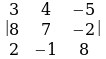
2. Дана матрица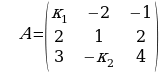 .
.
Найти
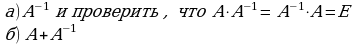
| Вариант | 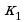
| 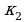
| Вариант | 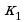
| 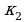
|
| 1 | 3 | -2 | 6 | 1 | 5 |
| 2 | 4 | 1 | 7 | -2 | 3 |
| 3 | 3 | -4 | 8 | 6 | -2 |
| 4 | 2 | 1 | 9 | -6 | 1 |
| 5 | 3 | -3 | 10 | -5 | 1 |







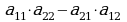 .
.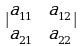
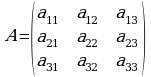 - квадратная матрица размера 3x3
- квадратная матрица размера 3x3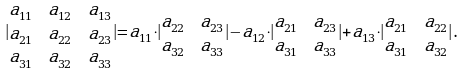
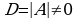 обратная матрица находится по формуле
обратная матрица находится по формуле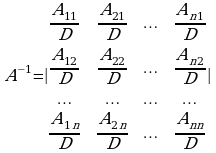
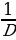
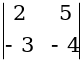 2)
2) 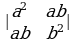 3)
3) 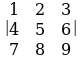 4)
4) 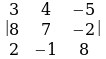
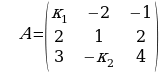 .
.