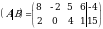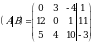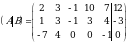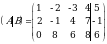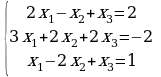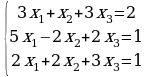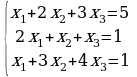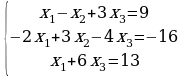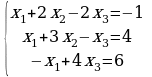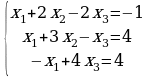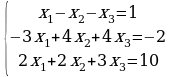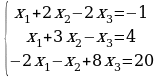Комплект контрольно-оценочных средств разработан на основе
Федерального государственного образовательного стандарта по специальности
среднего профессионального образования 23.02.07 Техническое обслуживание и ремонт двигателей, систем и агрегатов автомобилей, утвержденного приказом Министерства образования и науки от 9 декабря 2016 года № 1547 (зарегистрирован Министерством юстиции Российской Федерации 26 декабря 2016г., регистрационный №44936)
Просмотр содержимого документа
«Практическое занятие №8 Тема: «Решение систем линейных уравнений различными методами» (комплект КОС УЧЕБНОЙ ДИСЦИПЛИНЫ ЕН.01 МАТЕМАТИКА ДЛЯ СПЕЦИАЛЬНОСТИ СПО 23.02.07 ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ ДВИГАТЕЛЕЙ, СИСТЕМ И АГРЕГАТОВ АВТОМОБИЛЕЙ)»
Практическое занятие №8
Тема: «Решение систем линейных уравнений различными методами»
Цель: сформировать умение исследовать и использовать различные методы для решения систем линейных алгебраических уравнений
Теоретические сведения к практической работе
Алгоритм метода Гаусса. Цель рассуждений – путем элементарных преобразований свести исходную систему к равносильной, решение которой можно выписать непосредственно. Основными шагами метода Гаусса являются следующие.
I. Прямой ход. Выписать расширенную матрицу системы, путем элементарных преобразований свести ее к эквивалентной ступенчатой и определить ранги матрицы и расширенной матрицы системы. Если они различны, то исходная система несовместна, т.е. не имеет решений. Если 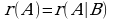 , то переходим к следующему этапу.
, то переходим к следующему этапу.
II. Сравнить ранг системы и число неизвестных, сделать вывод о количестве решений, учитывая теорему 2.
III. Обратный ход. Ступенчатую матрицу преобразовать к эквивалентной ей приведенной. Определить, какие неизвестные являются ведущими, какие – свободными.
IV. Выписать по полученной матрице систему, записать ответ (выразив, в случае неопределенной системы, ведущие элементы через свободные для построения общего решения).
Теорема Крамера. Рассмотрим «квадратную» систему линейных уравнений (число неизвестных совпадает с числом уравнений) вида
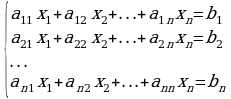 . (*)
. (*)
Если определитель матрицы системы (*) отличен от нуля (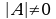 ), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам
), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам
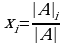 , i=1,2,…,n
, i=1,2,…,n
где 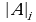 - определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.
- определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.
Содержание практической работы
Задание 1. По расширенной матрице выписать СЛАУ.
Задание 2. Решить системы уравнений методом Крамера и методом Гаусса.
Задание 3. Решить СЛАУ (в случае неопределенной системы выписывать общее и два любых частных решения).







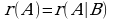 , то переходим к следующему этапу.
, то переходим к следующему этапу.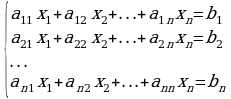 . (*)
. (*)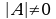 ), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам
), то данная система имеет единственное решение, причем значения неизвестных находятся по формулам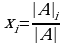 , i=1,2,…,n
, i=1,2,…,n 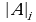 - определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.
- определитель матрицы, полученной из исходной матрицы системы путем замены i-го столбца на столбец свободных членов.