Просмотр содержимого документа
«Практическое занятие по теме "Формулы сложения и формулы удвоения"»
Практическое занятие
Формулы сложения и формулы удвоения.
1) Теоретический этап. Опорный конспект.
I. Формулы сложения.
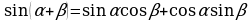
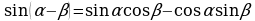
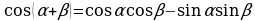
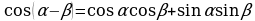
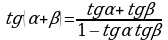
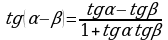
II. Формулы двойного аргумента.
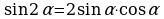
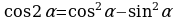 ;
; 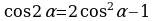 ;
; 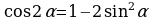
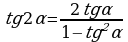
2) Подготовительный этап.
Пример 1. Вычислить:
а) cos 18°  cos 12°
cos 12° 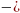 sin 18°
sin 18°  sin 12°; б) cos 107°
sin 12°; б) cos 107°  cos 17°
cos 17°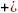 sin 107°
sin 107°  sin 17°;
sin 17°;
в) sin 17°  cos 13°
cos 13° 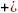 sin 13°
sin 13° cos 17°; г) sin 43°
cos 17°; г) sin 43° cos 13°
cos 13° 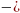 sin 13°
sin 13°  cos 43°;
cos 43°;
д) 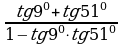 , е)
, е) 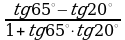 .
.
Решение: а) cos 18°  cos 12°
cos 12° 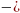 sin 18°
sin 18°  sin 12° = cos(18°
sin 12° = cos(18°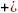 12°) = cos 30° = …
12°) = cos 30° = …
б) cos 107°  cos 17°
cos 17° 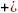 sin 107°
sin 107°  sin 17° = cos(107°
sin 17° = cos(107°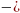 17°) = cos 90° = …
17°) = cos 90° = …
в) sin 17°  cos 13°
cos 13° 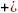 sin 13°
sin 13°  cos 17° = sin(17°
cos 17° = sin(17°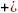 13°) = sin 30° = …
13°) = sin 30° = …
г) sin 43°  cos 13°
cos 13° 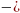 sin 13°
sin 13°  cos 43° = sin(43°
cos 43° = sin(43°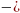 13°) = sin 30° = …
13°) = sin 30° = …
д) 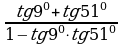 = tg (9°
= tg (9°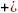 51°) = tg 60° = …
51°) = tg 60° = …
е) 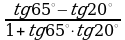 = tg (65°
= tg (65°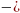 20°) = tg 45° = …
20°) = tg 45° = …
Ответ: а)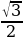 ; б) 0; в) 0,5; г) 0,5; д)
; б) 0; в) 0,5; г) 0,5; д) 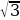 ; е) 1.
; е) 1.
Пример 2. Вычислить: а) cos 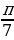
 cos
cos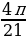
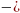 sin
sin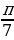
 sin
sin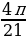 ;
;
б) sin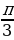
 cos
cos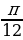
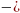 cos
cos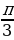
 sin
sin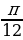
Решение: а) cos 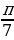
 cos
cos 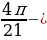 sin
sin 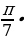 sin
sin 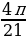 = cos (
= cos (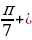
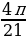 ) = cos (
) = cos (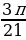
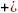
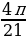 ) =
) =
= cos 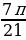 = cos
= cos 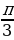 = …
= …
б) sin 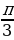
 cos
cos 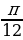
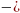 cos
cos 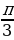
 sin
sin 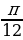 = sin(
= sin(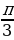
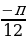 ) = sin (
) = sin ( 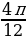
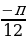 ) = sin
) = sin 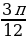 =
=
= sin 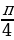 = …
= …
Ответ: а) 0,5; б) 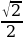 .
.
Пример 3. Упростить cos α  cos β
cos β 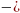 sin α
sin α  sin β, если α = 42 °, β = 18 °;
sin β, если α = 42 °, β = 18 °;
Решение:
cos α  cos β
cos β 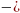 sin α
sin α  sin β = cos (α
sin β = cos (α 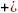 β) = cos (42 °
β) = cos (42 ° 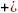 18 °) = cos 60 ° = …
18 °) = cos 60 ° = …
Ответ: 0,5
Пример 4. Вычислить: а) 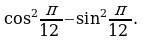 б)
б) 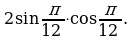
Решение: а) 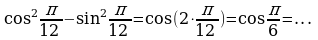
б) 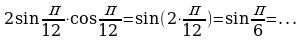
Ответ: а) 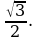 б)
б) 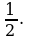
Пример 5. Дано: sin α = – 0,6, 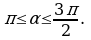
Найти: sin 2α
Решение: sin 2α = 2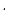 sinα
sinα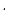 cosα . (Т.к.
cosα . (Т.к. 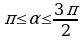 ,то cosα
,то cosα
cos α =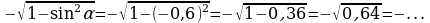
sin2α = 2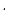 (
(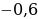 )
)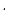 (
(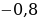 ) = ...
) = ...
Ответ: 0,96.
3) Практический этап.
Вычислить:
а) cos 38°  cos 22°
cos 22° 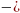 sin 38°
sin 38°  sin 22°;
sin 22°;
б) cos 55°  cos 10°
cos 10°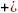 sin 55°
sin 55°  sin 10°;
sin 10°;
в) sin 47°  cos 13°
cos 13° 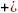 sin 13°
sin 13° cos 47°;
cos 47°;
г) sin 103° cos 13°
cos 13° 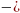 sin 13°
sin 13°  cos 103°;
cos 103°;
д) 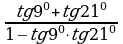 , е)
, е) 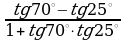 .
.
Вычислить:
а) cos 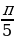
 cos
cos 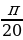
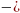 sin
sin 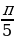
 sin
sin 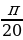
б) sin 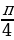
 cos
cos 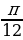
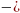 cos
cos 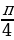
 sin
sin 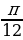 .
.
Упростить: cos α  cos β
cos β 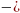 sin α
sin α  sin β, если α = 42 °, β = 48 °
sin β, если α = 42 °, β = 48 °
Вычислить: а) 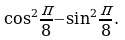 б)
б) 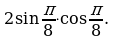
Дано: sinα = – 0,8, 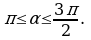 Найти: cos 2α
Найти: cos 2α
4) Дополнительные задания*
Вычислите: 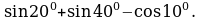
Вычислите: 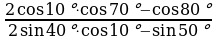
Упростите выражение: 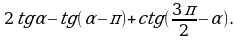
Вычислите: sin810° – cos900o + tg585o – ctg l845o + cos l35o – sin405°
Вычислить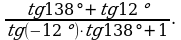
Упростите выражение 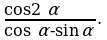
Упростите выражение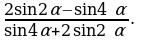
Найти значение выражения: 2sin150 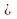 cos150.
cos150.
Найдите sin 2α, cos 2α,tg2α, если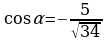 и
и 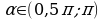







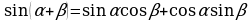
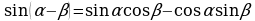
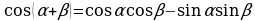
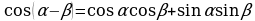
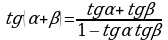
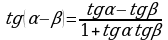
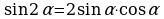
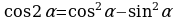 ;
; 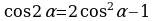 ;
; 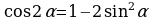
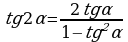
 cos 12°
cos 12°  sin 18°
sin 18°  sin 107°
sin 107° 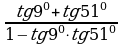 , е)
, е) 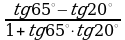 .
.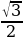 ; б) 0; в) 0,5; г) 0,5; д)
; б) 0; в) 0,5; г) 0,5; д) 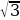 ; е) 1.
; е) 1.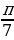
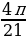
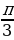
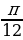
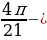 sin
sin 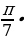 sin
sin 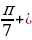
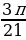
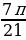 = cos
= cos 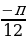 ) = sin (
) = sin ( 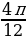
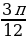 =
= 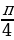 = …
= …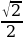 .
.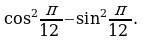 б)
б) 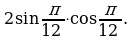
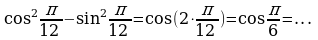
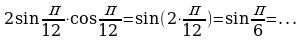
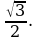 б)
б) 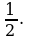
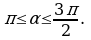
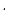 sinα
sinα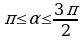 ,то cosα
,то cosα 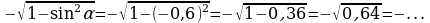
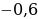 )
)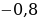 ) = ...
) = ...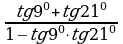 , е)
, е) 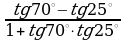 .
.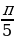
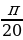
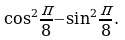 б)
б) 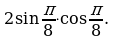
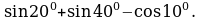
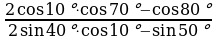
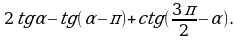
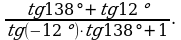
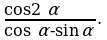
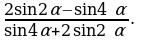
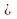 cos150.
cos150.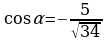 и
и