В разработке предложены задачи на построение угла, равного данному, биссектрисы угла, нахождение середины отрезка. Можно распечатать для каждого ученика.
Просмотр содержимого документа
«Практикум задач на построение по теме "Треугольники"»
Окружность.
1).Дана окружность с центром в точке О.
|
  А В А В  
С
D Как называется каждый | 

  О О
| 
 О О |
| из отрезков: | Построить : | Измерить радиус R= см |
| АО - | Хорду СВ | Построить хорду ВС=2см |
| ВС - | Диаметр СК | Построить хорду ВА=R |
| BD - | Радиус СО | Построить хорду ВМ = 2R, как называется такая хорда? |
2)
|
|
|
|
| Построить окружность R = 2см. | Построить две окружности R =2см, R=3см с общим центром. | Построить две касающиеся окружности. R =1см, R=2см. |
Построение биссектрисы угла.
С помощью транспортира построить биссектрису угла АОВ.
2)С помощью циркуля и линейки построить биссектрису угла.
Дано:
Построить: BD- биссектрису
Решение: Строим:
|
 А А
В С С |
1)Окр. (В.r), r – произвольный отрезок.
2) А и С – точки пересечения окр. (В,r) со сторонами угла.
3)Окр. (А,R), окр.(С,R), R – произвольный отрезок.
4) Точку D - пересечения окр. (А,R) и окр.(С,R)
5)Луч BD. |
3)Дан
| а ) )  А А

В С
| б  ) ) А
В С
| В)
А

В С
|
4) Постройте угол 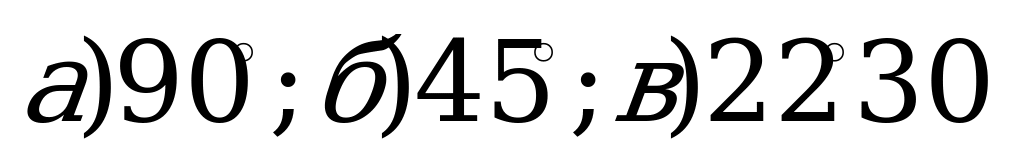
4) Постройте биссектрисы смежных углов. Найдите градусную меру угла между этими биссектрисами. Сделайте предполагаемый вывод.
Построение перпендикулярных прямых.
1)Построить проходящий через данную точку перпендикуляр к данной прямой (с помощью циркуля и линейки).
Дано: а – прямая, т. О
Построить: прямую ОС, перпендикулярную а .
Решение:
| т. О лежит на прямой
| т. О не лежит на прямой |
|
  О а
| 
а
 О
|
| 1)Строим окр. (О,r), r – любой отрезок;
2)т. А и В – т. пересечения прямой а и окр.(О,r);
3)строим окр. (А, АВ), окр.(В,АВ)
|
| 
4)т. С – точка пересечения окр. (А, АВ) и 4)т. С – т. пересечения окр.(А,АВ) и окр. (В, АВ.); окр. (В, АВ) в другой полуплоскости, не содержащей т. О; 5)строим прямую ОС. 5) строим прямую ОС.
|
Дан треугольник АВС. Построить точку пересечения его высот.
Сделать предполагаемый вывод.
Построение середины отрезка.
Разделить отрезок пополам (построить серединный перпендикуляр отрезка) с помощью циркуля и линейки.
Дано: отрезок АВ
Построить: т.О- средину АВ.
Решение:
|
  
А В
|
1)окр. (А,r), r- любой отрезок, больший половины отрезка АВ. 2) окр. (В, r); 3)точки С и 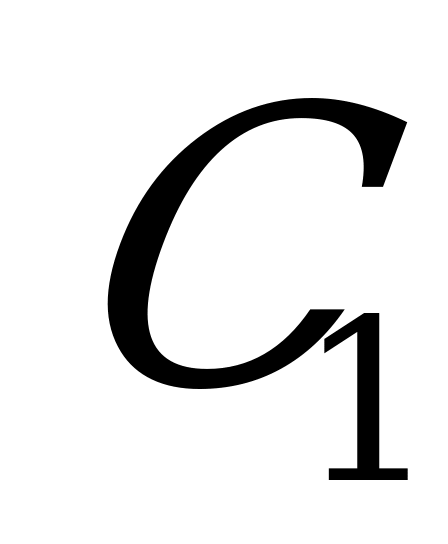 - пересечения окр. (А,r) и окр. (В,r); - пересечения окр. (А,r) и окр. (В,r); 4) прямую 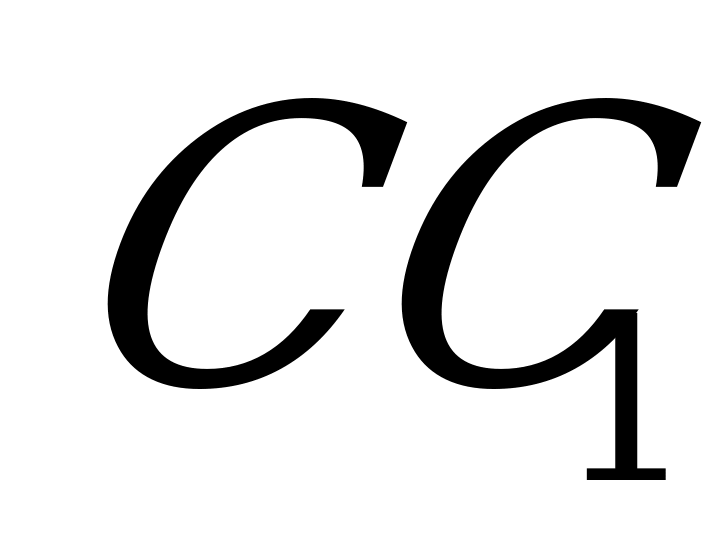 ; ; 5) точку О – точку пересечения прямых С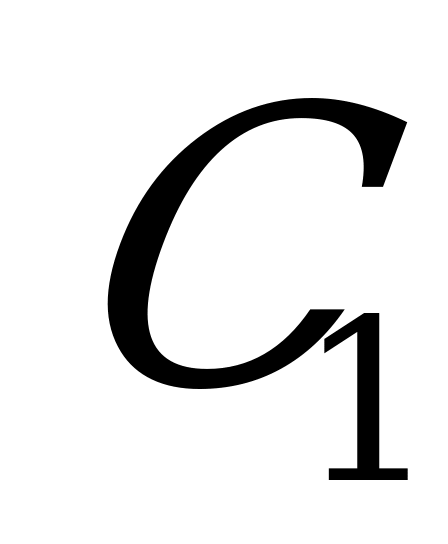 и АВ. и АВ.
|
Дан треугольник АВС. Построить точку пересечения его медиан.
Сделать предполагаемый вывод.
3) Разделить данный отрезок на: а) 2 равных отрезка; б) 4 равных отрезка;
в) 8 равных отрезков.
С помощью транспортира построить биссектрису угла АОВ.
1)Построить проходящий через данную точку перпендикуляр к данной прямой (с помощью циркуля и линейки).
Решение:
Построение угла, равного данному.
1)С помощью циркуля и линейки построить угол, равный данному.
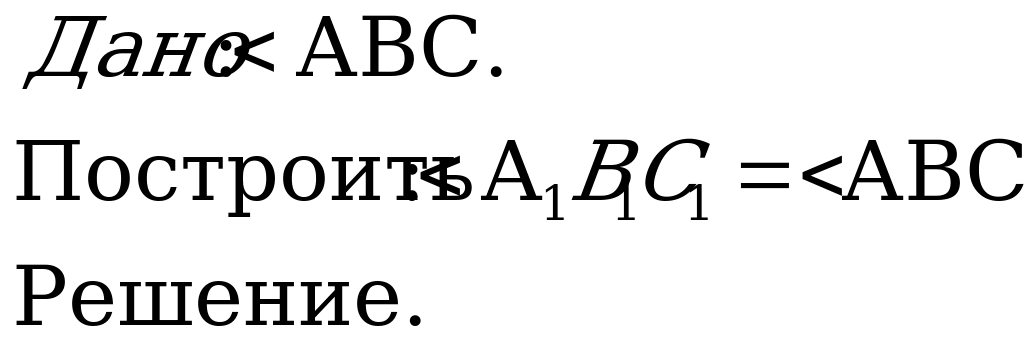 Строим:
Строим:
|
 А А 
r
  С В
|
 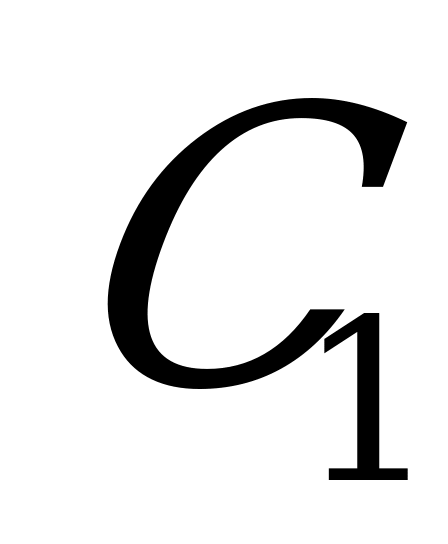 
| 1) Окр.( С,r),r-любой радиус 2) Точки А и В – т. пересечения окружности со сторонами 3) Луч с началом в точке 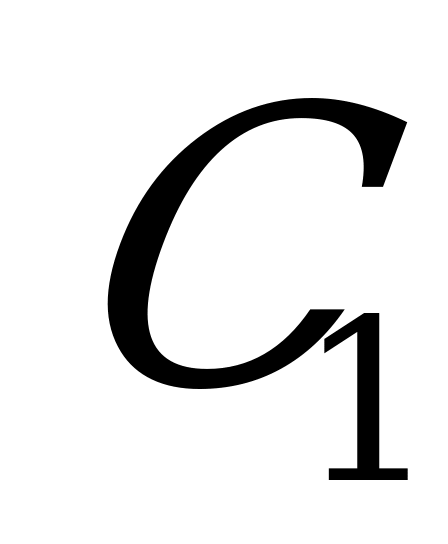 . . 4) Строим окр.(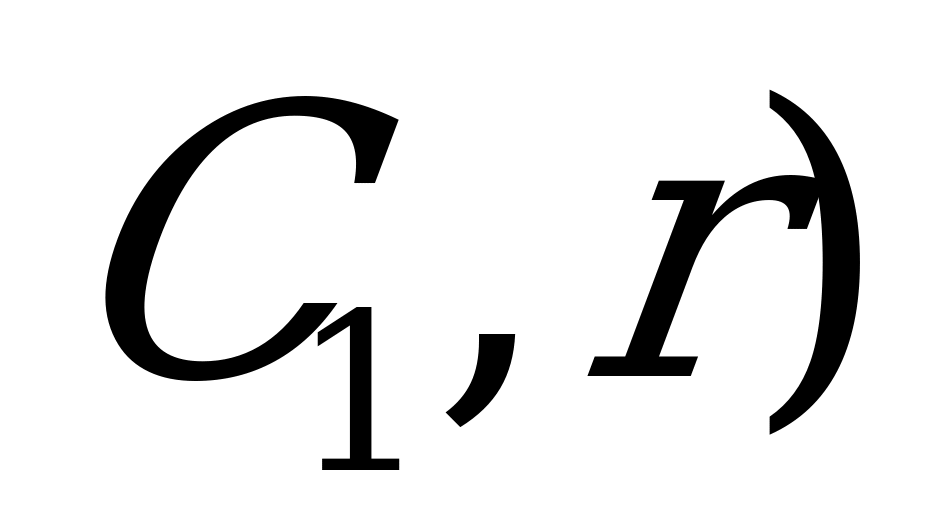 5)Точка 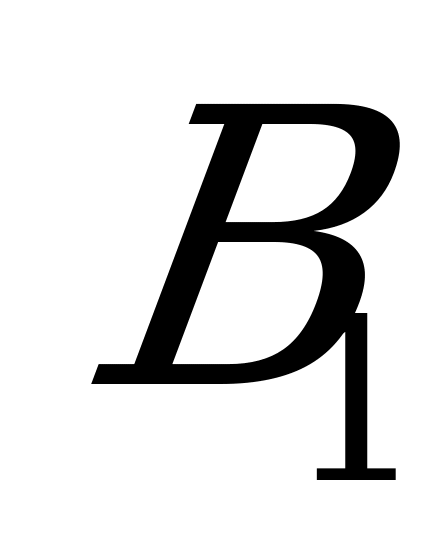 -т. пересечения луча с окр.( -т. пересечения луча с окр.(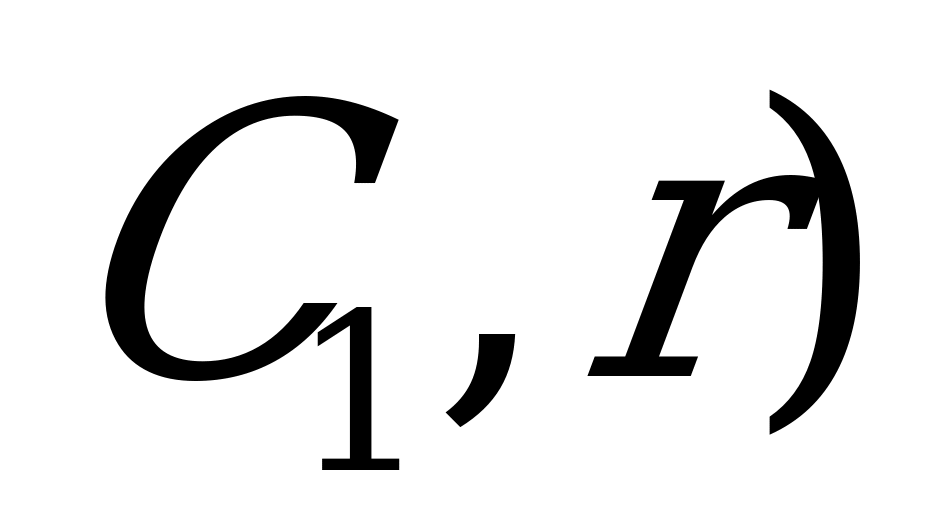 . . 6) Окр. (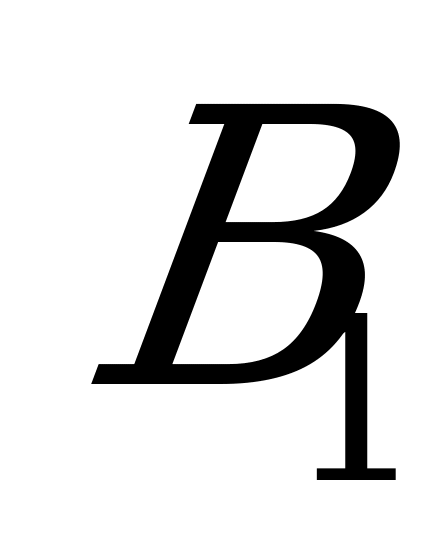 ,ВА). ,ВА). 7) Точка  - т. пересечения окр. ( - т. пересечения окр. (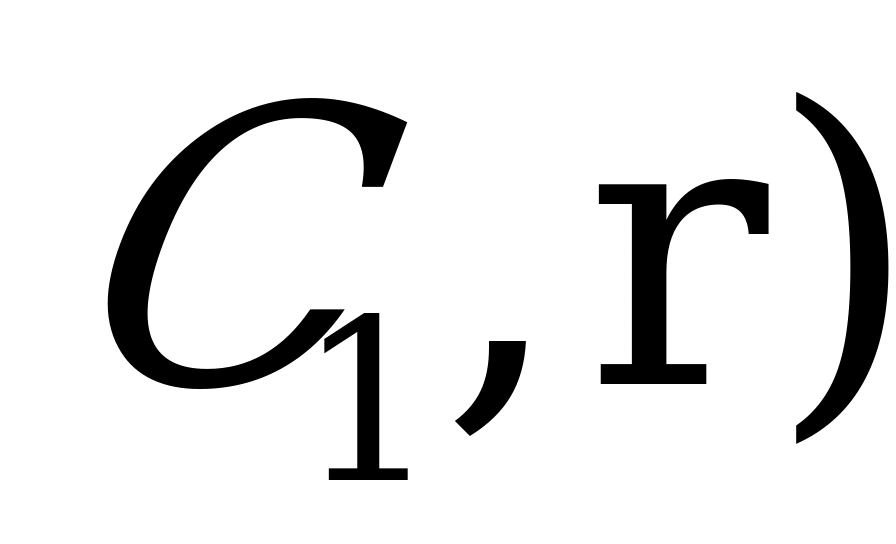 и окр. ( и окр. ( , ВА) , ВА) 8) Луч 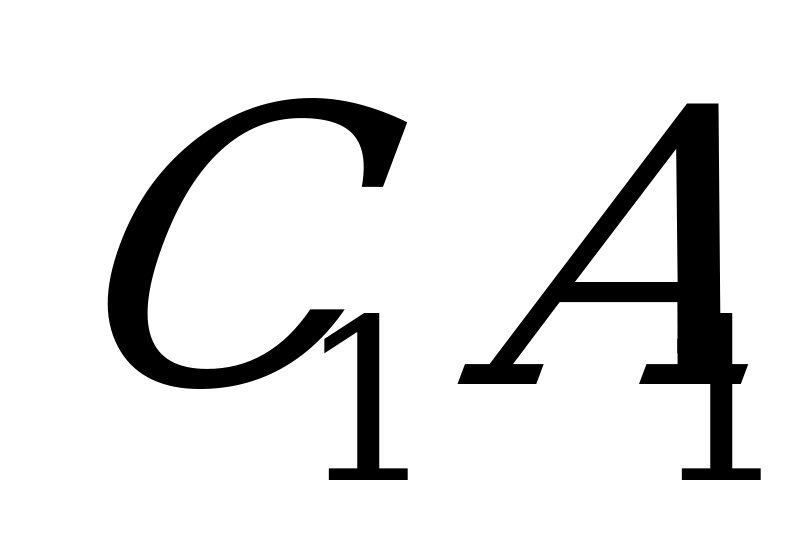 9)
|
2) Построить разность двух данных углов.
3) Построить сумму двух данных углов.







 А В
А В
 А
А О
О



 А
А С
С )
) А
А

 )
)







 А
А








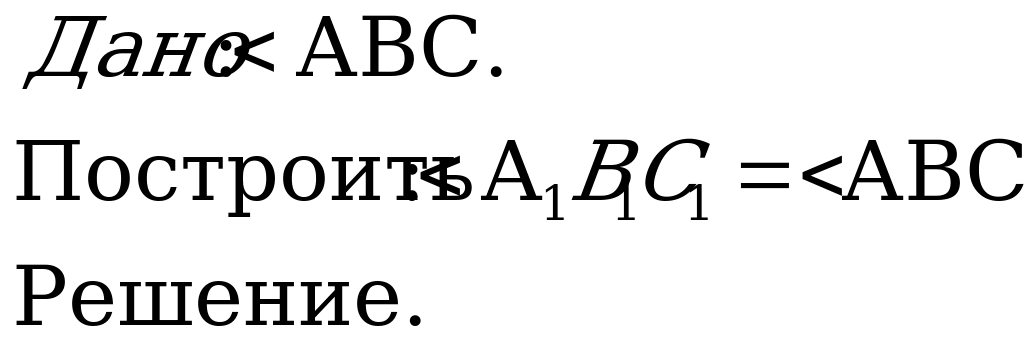 Строим:
Строим: А
А