Правильные многоугольники.

Правильные многоугольники

Автор – Софронова Наталия Андреевна, учитель математики МОУ «Упшинская основная общеобразовательая школа»

К учебнику «Геометрия 7-9» под редакцией Атанасяна

Определение правильного многоугольника

Правильным многоугольником называется выпуклый многоугольник, у которого

все углы равны и все стороны равны

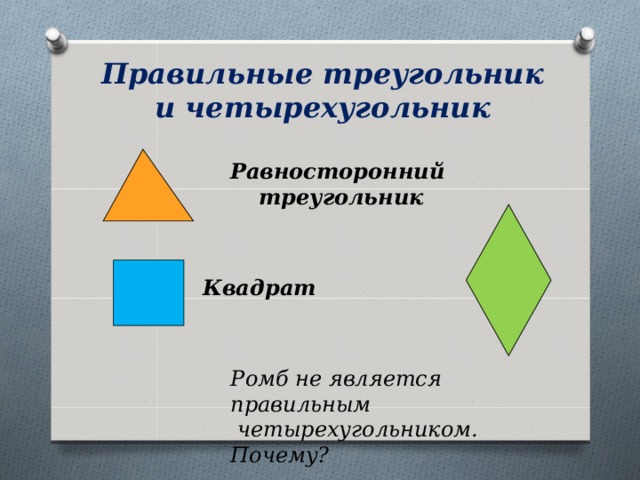
Правильные треугольник и четырехугольник

Равносторонний

треугольник

Квадрат

Ромб не является правильным

четырехугольником. Почему?

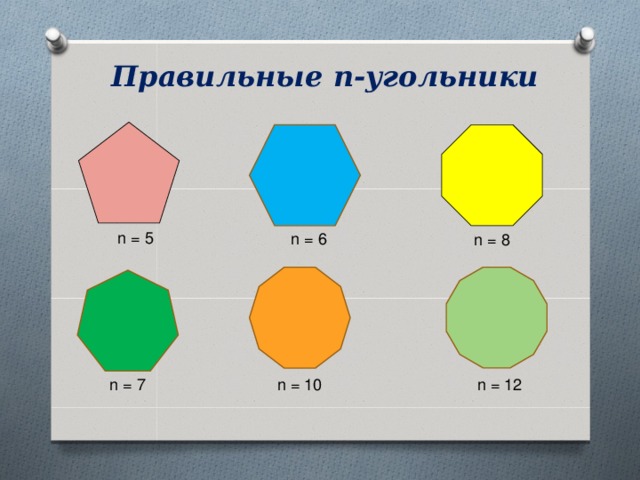
Правильные n-угольники

n = 5

n = 6

n = 8

n = 7

n = 10

n = 12

Сумма углов многоугольника

Сумма углов выпуклого многоугольника вычисляется по формуле: ∑ углов n-уг. = 180 0 (n - 2)

Сумма углов выпуклого семиугольника равна:

∑ углов 7-уг . = 180 0 · (7 - 2) = 900 0

Сумма углов выпуклого одиннадцатиугольника равна: ∑ углов 11-уг . = 180 0 · (11 - 2) =1620 0

Нахождение градусной меры угла правильного n - угольника α n

Кол-во сторон n

Сумма всех углов

∑ углов n-уг.

n

Величина одного угла

α n

С.У. n = 180 0 (n-2)

8

180 0 (8-2)=1080 0

10

1080 0 : 8=135 0

180 0 (10-2)=1440 0

1440 0 :10=144 0

Внешний угол правильного n - угольника

Внешний угол – это угол, смежный с внутренним.

Сумма внешних углов любого многоугольника равна 360 0 .

Внешний угол правильного n-угольника равен

Задача. Сколько сторон имеет правильный многоугольник, если его угол равен 150 0 ?

1 способ

n-количество сторон

Сумма углов равна 180 0 (n-2) или 150 0 n

Имеем уравнение:

180 0 (n-2)=150 0 n

180 0 n-360=150 0 n

30n = 360

n = 12

2 способ

Внешний угол многоугольника равен 180 0 – 150 0 = 30 0 .

n-количество сторон, углов

n = 360 0 : 30 0 = 12

Правильный многоугольник и окружность

Теорема. Около любого правильного многоугольника можно описать окружность, и притом только одну.

Около правильного многоугольника можно описать окружность, и только одну.

Центр окружности –

точка пересечения биссектрис

Радиус – отрезок, соединяющий центр с любой вершиной многоугольника

А 3

4

О

А 2

Единственность: так как через какие-нибудь три вершины многоугольника (например. А1, А2, А3) проходит только одна окружность, то около многоугольника можно описать только одну окружность

3

1

2

А 1

Пусть точка О – точка пересечения биссектрис углов А 1 и А 2

Δ А 1 А 2 О – равнобедренный (почему?)

ОА 1 = ОА 2

Δ А 1 А 2 О = Δ А 2 А 3 О (почему?)

ОА 2 = ОА 3

Аналогично ОА 3 = ОА 4 , ОА 4 = ОА 5 ….

Вывод ОА 1 = ОА 2 = ОА 3 = ОА 4 = ОА 5 = …. Точка О равноудалена от всех вершин многоугольника, О центр - описанной окружности

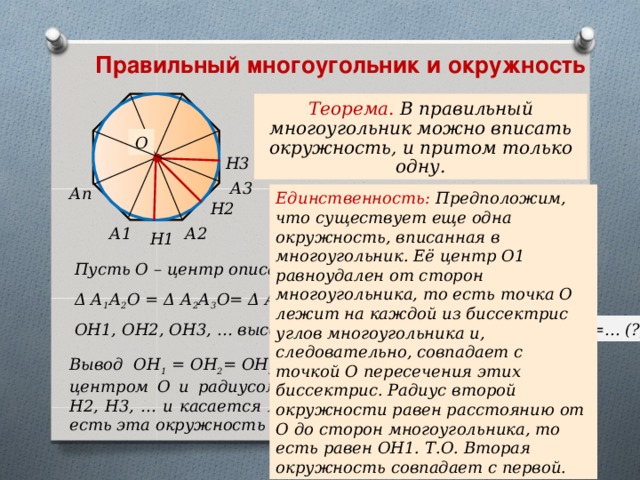
Правильный многоугольник и окружность

Теорема. В правильный многоугольник можно вписать окружность, и притом только одну.

О

Н3

А3

А n

Единственность: Предположим, что существует еще одна окружность, вписанная в многоугольник. Её центр О1 равноудален от сторон многоугольника, то есть точка О лежит на каждой из биссектрис углов многоугольника и, следовательно, совпадает с точкой О пересечения этих биссектрис. Радиус второй окружности равен расстоянию от О до сторон многоугольника, то есть равен ОН1. Т.О. Вторая окружность совпадает с первой.

Н2

А1

А2

Н1

Пусть О – центр описанной окружности

Δ А 1 А 2 О = Δ А 2 А 3 О= Δ А 3 А 4 О = ...

ОН1, ОН2, ОН3, … высоты этих треугольников

ОН1=ОН2=ОН3=… (?)

Вывод ОН 1 = ОН 2 = ОН 3 = ОН 4 = ОН 5 = …. Окружность с центром О и радиусом ОН1 проходит через точки Н1, Н2, Н3, … и касается многоугольника в этих точках, то есть эта окружность вписана в многоугольник.

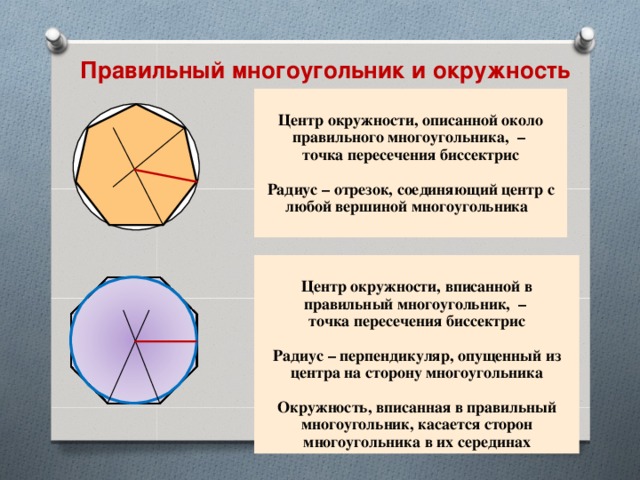
Правильный многоугольник и окружность

Центр окружности, описанной около правильного многоугольника, –

точка пересечения биссектрис

Радиус – отрезок, соединяющий центр с любой вершиной многоугольника

Центр окружности, вписанной в правильный многоугольник, –

точка пересечения биссектрис

Радиус – перпендикуляр, опущенный из центра на сторону многоугольника

Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах

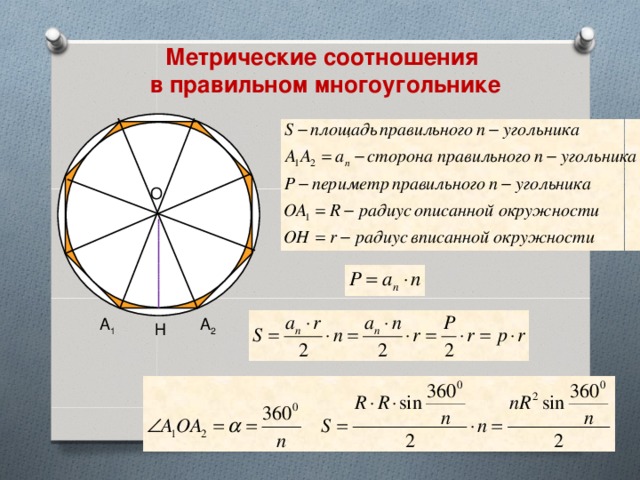
Метрические соотношения

в правильном многоугольнике

О

А 1

А 2

Н

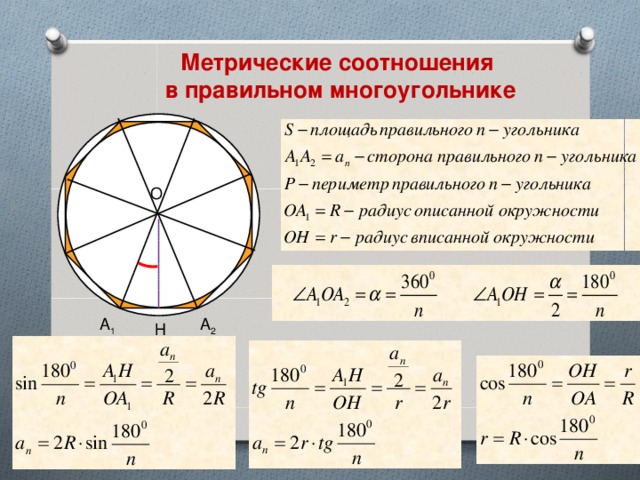
Метрические соотношения

в правильном многоугольнике

О

А 1

А 2

Н

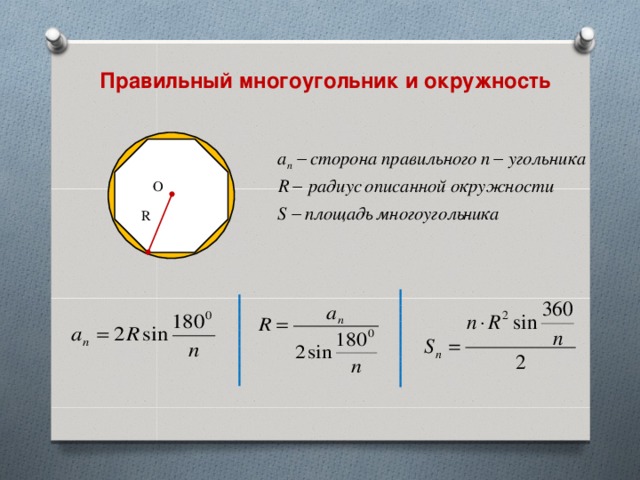
Правильный многоугольник и окружность

О

R

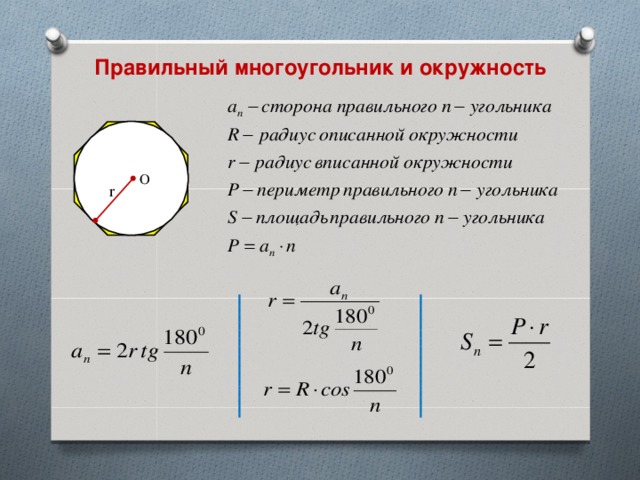
Правильный многоугольник и окружность

О

r

Правильный многоугольник и окружность

n

R

а n - сторона

r

n = 3

S n

n = 4

n = 6

а