Правильные многогранники»

 Дата проведения:

Предмет: математика

Преподаватель: Касымова У.Ш.

Группа:

Тема:   « Правильные многогранники»  

Цель урока: Познакомить учащихся с новым типом выпуклых многогранников – правильными многогранниками.

Задачи урока:

1. Обучающие:   Ввести понятие правильного многогранника, рассмотреть свойства правильных многогранников.

1. Развивающие:  Формирование пространственных представлений учащихся. Формирование умения обобщать, систематизировать, видеть закономерности. Развитие монологической речи учащихся.

1.  Воспитательные: Воспитание эстетического чувства. Воспитание умения слушать. Формирование интереса к предмету.

Оборудование:  раздаточный материал (рабочие листы)

Литература: А.В. Погорелов 10-11кл

Ход урока:

1. Организационный момент.    Целевая установка урока  (Сообщение темы, цели урока и  порядка работы.)

 Откройте тетради и запишите классная работа, тема « Правильные многогранники».

2. Актуализация знаний.

1.  Правильных многогранников много.

2. Правильные многогранники могут быть выпуклыми  и не выпуклыми.

3. Для правильных многогранников действует эйлерова характеристика.

3. Одноклеточный организм феодарии (Circjgjnia icosahtdra) по форме напоминает правильный  икосаэдр.

4. Кристаллы поваренной соли имеют форму куба;
5. Существует  модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер.

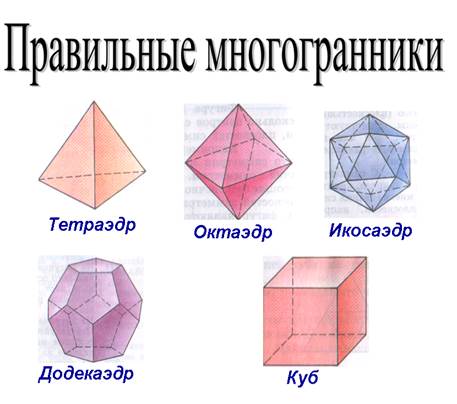
 «Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)»

Теоретическая часть:

Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n ≥ 6.

Сумма всех плоских углов при каждой вершине выпуклого правильного многогранника меньше 360⁰.

Существует всего пять видов правильных многогранников:

1. Правильный тетраэдр – составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180⁰.

2. Правильный октаэдр – составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240⁰.

3. Правильный икосаэдр – составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300⁰.

4. Правильный гексаэдр (куб) – составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270⁰.

5. Правильный додекаэдр – составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324⁰.

Практическая часть:

Задача № 1

Найдите угол между двумя диагоналями граней куба, имеющими общий конец.

Решение

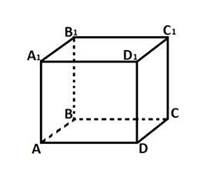
Пусть a – ребро куба, A₁B и A₁C₁ – диагонали. Значит ∠ BA₁C₁ – искомый.

1) Так как все грани куба – равные квадраты, то диагонали граней равны, то есть A₁B=A₁C=BC₁= .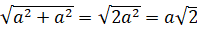

2) ΔA₁BC₁ – равносторонний, значит ∠ BA₁C₁=60⁰.

Ответ: 60⁰

Итог урока:

    Подходит к концу урок, подведём итоги.  

Домашнее задание

№ 1 Склеить модели правильных многогранников на выбор;

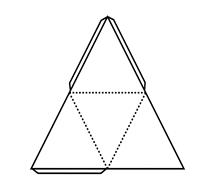
Перерисуйте развертку правильного тетраэдра на плотный лист бумаги в большем масштабе, вырежьте развертку (сделав необходимые припуски для склеивания) и склейте из нее тетраэдр. На фигуре подпишите название, число вершин, ребер и граней.

№ 3

Перерисуйте развертку правильного октаэдра на плотный лист бумаги в большем масштабе, вырежьте развертку (сделав необходимые припуски для склеивания) и склейте из нее октаэдр. На фигуре подпишите название, число вершин, ребер и граней.

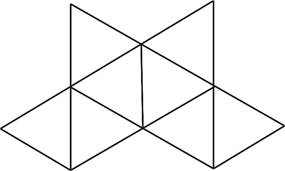
№ 4

Перерисуйте развертку правильного додекаэдра на плотный лист бумаги в большем масштабе, вырежьте развертку (сделав необходимые припуски для склеивания) и склейте из нее додекаэдр. На фигуре подпишите название, число вершин, ребер и граней.

.
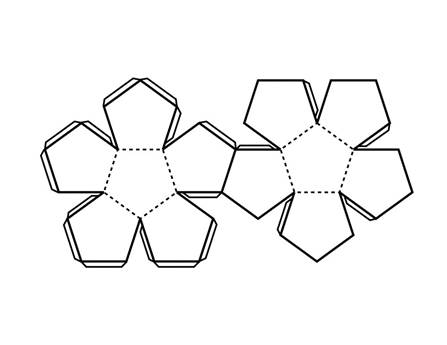