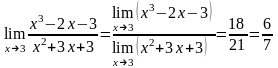Практическая работа
«Вычисление пределов. Раскрытие неопределенностей»
Цель работы: научиться вычислять пределы, раскрывать неопределенности.
Краткие теоретические и учебно-методические материалы по теме практической работы
Пусть функция f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хnа, сходящейся к а, последовательность соответствующих значений функции f(xn), nN сходится к числу В.
В этом случае пишут: 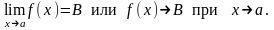
Свойства пределов сформулируем в виде теорем:
Теорема 1: Функция не может иметь двух разных пределов в точке.
Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют:
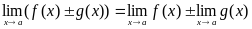 .
.
Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют:
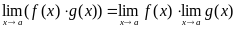 .
.
Следствие: Постоянный множитель можно выносить за знак предела, т.е.
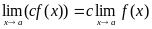 .
.
Теорема 4: Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:
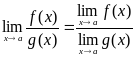 .
.
Дадим определение предела функции f(x) на бесконечности, т.е. х+ и при х-.
Пусть функция f(x) определена на всей числовой прямой. Число В называется пределом функции f(x) при х+, если 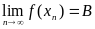 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что 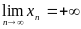 . В этом случае пишут
. В этом случае пишут 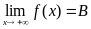 . Аналогично,
. Аналогично, 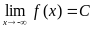 , если
, если 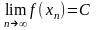 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что  В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции
В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции 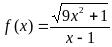 , определенной для всех х 1, имеем:
, определенной для всех х 1, имеем:
 ,
, 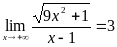 .
.
Поэтому при исследовании свойств функций рассматривают как 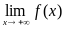 , так и
, так и 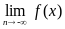 .
.
Сформулируем определение бесконечного предела функции:
Если для любой последовательности значений аргумента (xn) такой, что xn а имеет место 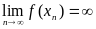 , то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут
, то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут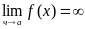 .
.
3) Применение замечательных пределов 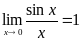 и
и 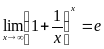
Здесь мы воспользовались известным пределом  .
.
Примеры по выполнению практической работы
Пример 1. Пусть требуется вычислить 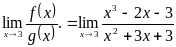
Решение: f (x) = x3 – 2x – 3 и g (x) = x2 + 3x + 3. Так как g (3) = 32 + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем: 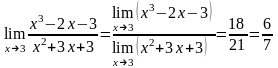
Пример 2. Вычислить 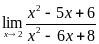 .
.
Решение: здесь ƒ (2) = 22 - 5∙2 + 6 = 0, g (2) = 22 - 6∙2 + 8 = 0. Так как x ≠ 2, имеем
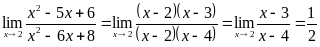 .
.
Пример 3. Вычислить .
Решение:
.
Пример 4. Вычислить .
.
Пример 5. Вычислить .
Решение: .
Пример 6. Вычислить .
Пример 7. Найти предел .
= = = =0
=0
Пример 8. Вычислить 
Решение: , заменяя 3x = y и учитывая, что y → 0 при
x → 0, получаем: .
Пример 9. Вычислить .
Решение:
Пример 10. Вычислить
Решение:
Задания для практического занятия:
Вариант 1
1. Вычислить пределы функций в точке:
а) ; б)  ; в) ; г) ;
; в) ; г) ;
2. Вычислить пределы функций на бесконечности:
а) ; б)  ; в) ; г) - домножить на сопряжённое выражение и разделить числитель и знаменатель дроби на х!
; в) ; г) - домножить на сопряжённое выражение и разделить числитель и знаменатель дроби на х!
3. Вычислить, используя замечательные пределы:
а)  ; б) ; в) ; г)
; б) ; в) ; г)
Контрольные вопросы
1.Что называется пределом функции в точке? На бесконечности?
2.Какие свойства пределов функций вы знаете?
3.Как раскрывать неопределенности?
4.Какие замечательные пределы вы знаете?
Практическая работа
«Вычисление пределов. Раскрытие неопределенностей»
Цель работы: научиться вычислять пределы, раскрывать неопределенности.
Краткие теоретические и учебно-методические материалы по теме практической работы
Пусть функция f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хnа, сходящейся к а, последовательность соответствующих значений функции f(xn), nN сходится к числу В.
В этом случае пишут: 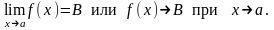
Свойства пределов сформулируем в виде теорем:
Теорема 1: Функция не может иметь двух разных пределов в точке.
Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют:
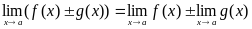 .
.
Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют:
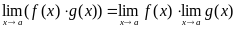 .
.
Следствие: Постоянный множитель можно выносить за знак предела, т.е.
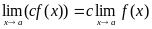 .
.
Теорема 4: Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:
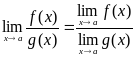 .
.
Дадим определение предела функции f(x) на бесконечности, т.е. х+ и при х-.
Пусть функция f(x) определена на всей числовой прямой. Число В называется пределом функции f(x) при х+, если 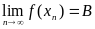 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что 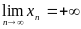 . В этом случае пишут
. В этом случае пишут 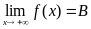 . Аналогично,
. Аналогично, 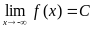 , если
, если 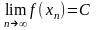 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что  В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции
В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции 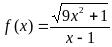 , определенной для всех х 1, имеем:
, определенной для всех х 1, имеем:
 ,
, 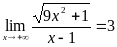 .
.
Поэтому при исследовании свойств функций рассматривают как 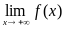 , так и
, так и 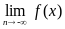 .
.
Сформулируем определение бесконечного предела функции:
Если для любой последовательности значений аргумента (xn) такой, что xn а имеет место 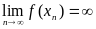 , то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут
, то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут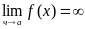 .
.
3) Применение замечательных пределов 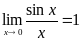 и
и 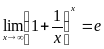
Здесь мы воспользовались известным пределом  .
.
Примеры по выполнению практической работы
Пример 1. Пусть требуется вычислить 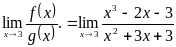
Решение: f (x) = x3 – 2x – 3 и g (x) = x2 + 3x + 3. Так как g (3) = 32 + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем: 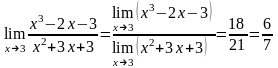
Пример 2. Вычислить 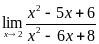 .
.
Решение: здесь ƒ (2) = 22 - 5∙2 + 6 = 0, g (2) = 22 - 6∙2 + 8 = 0. Так как x ≠ 2, имеем
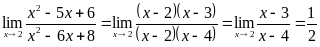 .
.
Пример 3. Вычислить .
Решение:
.
Пример 4. Вычислить .
.
Пример 5. Вычислить .
Решение: .
Пример 6. Вычислить .
Пример 7. Найти предел .
= = = =0
=0
Пример 8. Вычислить 
Решение: , заменяя 3x = y и учитывая, что y → 0 при
x → 0, получаем: .
Пример 9. Вычислить .
Решение:
Пример 10. Вычислить
Решение:
Задания для практического занятия:
Вариант 2
1. Вычислить пределы функций в точке:
а) ; б) ; в) ; г) ;
2. Вычислить пределы функций на бесконечности:
а) ; б) ; в) ; г) - домножить на сопряжённое выражение и разделить числитель и знаменатель дроби на х!
3. Вычислить, используя замечательные пределы:
а)  ; б) ; в ) ; г)
; б) ; в ) ; г)  ;
;
Контрольные вопросы
1.Что называется пределом функции в точке? На бесконечности?
2.Какие свойства пределов функций вы знаете?
3.Как раскрывать неопределенности?
4.Какие замечательные пределы вы знаете?
Практическая работа
«Вычисление пределов. Раскрытие неопределенностей»
Цель работы: научиться вычислять пределы, раскрывать неопределенности.
Краткие теоретические и учебно-методические материалы по теме практической работы
Пусть функция f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хnа, сходящейся к а, последовательность соответствующих значений функции f(xn), nN сходится к числу В.
В этом случае пишут: 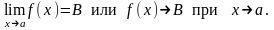
Свойства пределов сформулируем в виде теорем:
Теорема 1: Функция не может иметь двух разных пределов в точке.
Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют:
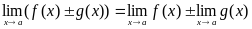 .
.
Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют:
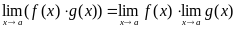 .
.
Следствие: Постоянный множитель можно выносить за знак предела, т.е.
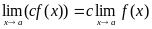 .
.
Теорема 4: Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:
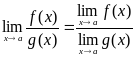 .
.
Дадим определение предела функции f(x) на бесконечности, т.е. х+ и при х-.
Пусть функция f(x) определена на всей числовой прямой. Число В называется пределом функции f(x) при х+, если 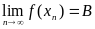 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что 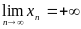 . В этом случае пишут
. В этом случае пишут 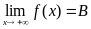 . Аналогично,
. Аналогично, 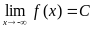 , если
, если 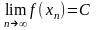 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что  В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции
В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции 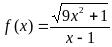 , определенной для всех х 1, имеем:
, определенной для всех х 1, имеем:
 ,
, 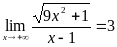 .
.
Поэтому при исследовании свойств функций рассматривают как 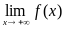 , так и
, так и 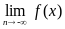 .
.
Сформулируем определение бесконечного предела функции:
Если для любой последовательности значений аргумента (xn) такой, что xn а имеет место 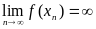 , то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут
, то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут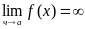 .
.
3) Применение замечательных пределов 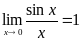 и
и 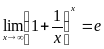
Здесь мы воспользовались известным пределом  .
.
Примеры по выполнению практической работы
Пример 1. Пусть требуется вычислить 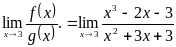
Решение: f (x) = x3 – 2x – 3 и g (x) = x2 + 3x + 3. Так как g (3) = 32 + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем: 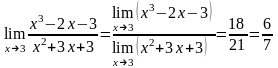
Пример 2. Вычислить 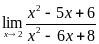 .
.
Решение: здесь ƒ (2) = 22 - 5∙2 + 6 = 0, g (2) = 22 - 6∙2 + 8 = 0. Так как x ≠ 2, имеем
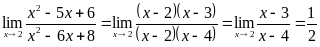 .
.
Пример 3. Вычислить .
Решение:
.
Пример 4. Вычислить .
.
Пример 5. Вычислить .
Решение: .
Пример 6. Вычислить .
Пример 7. Найти предел .
= = = =0
=0
Пример 8. Вычислить 
Решение: , заменяя 3x = y и учитывая, что y → 0 при
x → 0, получаем: .
Пример 9. Вычислить .
Решение:
Пример 10. Вычислить
Решение:
Задания для практического занятия:
Вариант 3
1. Вычислить пределы функций в точке:
а) ; б) ; в) ; г) ;
2. Вычислить пределы функций на бесконечности:
а) ; б) ; в) ; г) - домножить на сопряжённое выражение и разделить числитель и знаменатель дроби на х!
3. Вычислить, используя замечательные пределы:
а) ; б) ; в)  ; г) ;
; г) ;
Контрольные вопросы
1.Что называется пределом функции в точке? На бесконечности?
2.Какие свойства пределов функций вы знаете?
3.Как раскрывать неопределенности?
4.Какие замечательные пределы вы знаете?
Практическая работа
«Вычисление пределов. Раскрытие неопределенностей»
Цель работы: научиться вычислять пределы, раскрывать неопределенности.
Краткие теоретические и учебно-методические материалы по теме практической работы
Пусть функция f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хnа, сходящейся к а, последовательность соответствующих значений функции f(xn), nN сходится к числу В.
В этом случае пишут: 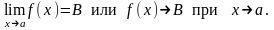
Свойства пределов сформулируем в виде теорем:
Теорема 1: Функция не может иметь двух разных пределов в точке.
Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют:
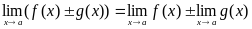 .
.
Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют:
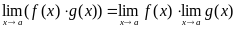 .
.
Следствие: Постоянный множитель можно выносить за знак предела, т.е.
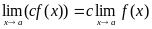 .
.
Теорема 4: Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:
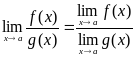 .
.
Дадим определение предела функции f(x) на бесконечности, т.е. х+ и при х-.
Пусть функция f(x) определена на всей числовой прямой. Число В называется пределом функции f(x) при х+, если 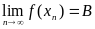 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что 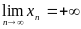 . В этом случае пишут
. В этом случае пишут 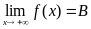 . Аналогично,
. Аналогично, 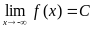 , если
, если 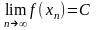 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что  В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции
В ряде случаев поведение функции f(x) разное при х+ и при х-. Например, для функции 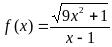 , определенной для всех х 1, имеем:
, определенной для всех х 1, имеем:
 ,
, 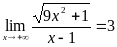 .
.
Поэтому при исследовании свойств функций рассматривают как 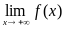 , так и
, так и 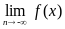 .
.
Сформулируем определение бесконечного предела функции:
Если для любой последовательности значений аргумента (xn) такой, что xn а имеет место 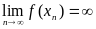 , то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут
, то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут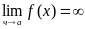 .
.
3) Применение замечательных пределов 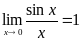 и
и 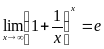
Здесь мы воспользовались известным пределом  .
.
Примеры по выполнению практической работы
Пример 1. Пусть требуется вычислить 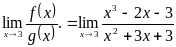
Решение: f (x) = x3 – 2x – 3 и g (x) = x2 + 3x + 3. Так как g (3) = 32 + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем: 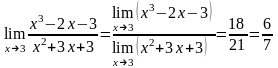
Пример 2. Вычислить 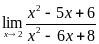 .
.
Решение: здесь ƒ (2) = 22 - 5∙2 + 6 = 0, g (2) = 22 - 6∙2 + 8 = 0. Так как x ≠ 2, имеем
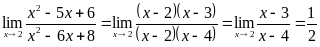 .
.
Пример 3. Вычислить .
Решение:
.
Пример 4. Вычислить .
.
Пример 5. Вычислить .
Решение: .
Пример 6. Вычислить .
Пример 7. Найти предел .
= = = =0
=0
Пример 8. Вычислить 
Решение: , заменяя 3x = y и учитывая, что y → 0 при
x → 0, получаем: .
Пример 9. Вычислить .
Решение:
Пример 10. Вычислить
Решение:
Задания для практического занятия:
Вариант 4
1. Вычислить пределы функций в точке:
а) ; б) ; в) ; г) ;
2. Вычислить пределы функций на бесконечности:
а) ; б) ; в) ; г) - домножить на сопряжённое выражение и разделить числитель и знаменатель дроби на х!
3. Вычислить, используя замечательные пределы:
а) ; б) ; в) ; г)  ;
;
Контрольные вопросы
1.Что называется пределом функции в точке? На бесконечности?
2.Какие свойства пределов функций вы знаете?
3.Как раскрывать неопределенности?
4.Какие замечательные пределы вы знаете?





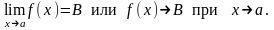
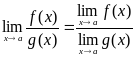 .
.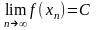 для любой последовательности (xn) такой, что
для любой последовательности (xn) такой, что