| Отделение , группа ___ Семестр ___3___, курс__2____ Преподаватель Пластун СВ (Ф.И.О.) Предмет:” Элементы высшей математики Т.З. Лекция № 4 ”Тема« Определители Определитель квадратной матрицы. Свойства определителей Способы вычисления определителей.» |
1. Определитель квадратной матрицы.
Всякой квадратной матрице можно поставить в соответствие действительное число, называемое определителем или детерминантом этой матрицы.
Для определителя матрицы A применяются различные обозначения. Укажем наиболее употребимые: detA, D , или развернутое, указывающее на связь с данной матрицей
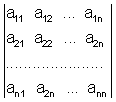 . (1)
. (1)
Прямые скобки, заменяющие круглые (матричные), указывают на то, что имеется в виду именно определитель матрицы, т.е. единственное число, а не сама матрица A.
Рассмотрим определитель 2-го порядка 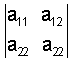 .
.
Чтобы найти значение этого определителя надо перемножить элементы главной диагонали и отнять от полученного числа произведение элементов побочной диагонали, т.е. 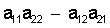 . (2)
. (2)
Например, определитель 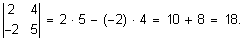
Определитель 3-го порядка 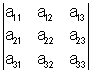 вычисляется по формуле
вычисляется по формуле
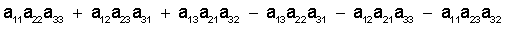 . (3)
. (3)
Например, 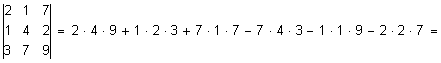
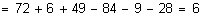 .
.
Для того чтобы определить правило вычисления определителей порядка выше, чем 3, введем сначала некоторые новые объекты.
Пусть нам дана квадратная матрица порядка n
 . (4)
. (4)
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
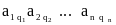 , (5)
, (5)
где индексы q1, q2,..., qn составляют некоторую перестановку из чисел
1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (- 1)q, где q - число инверсий в перестановке вторых индексов элементов.
Определителем n -го порядка, соответствующим матрице (4), называется алгебраическая сумма n! членов вида 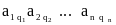 .
.
2. Свойства определителей
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j=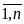 ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
3. Способы вычисления определителей.
Минором Mi j элемента ai j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j. (6)
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = ai 1 Ai 1 + ai 2 Ai 2 +... + ai n Ai n (i = 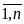 ) (7)
) (7)
или j- го столбца
d = a1 j A1 j + a2 j A2 j +... + an j An j (j = 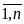 ). (7а)
). (7а)
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример 1. Не вычисляя определителя 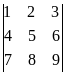 , показать, что он равен нулю.
, показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель 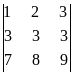 , равный исходному. Если из третьей строки также вычесть первую, то получится определитель
, равный исходному. Если из третьей строки также вычесть первую, то получится определитель 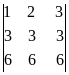 , в котором две строки пропорциональны. Такой определитель равен нулю.
, в котором две строки пропорциональны. Такой определитель равен нулю.
Пример 2. Вычислить определитель D = 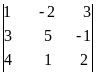 , разложив его по элементам второго столбца.
, разложив его по элементам второго столбца.
Решение. Разложим определитель по элементам второго столбца:
D = a12A12 + a22A22+a32A32=
= 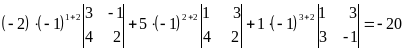 .
.
Пример 3. Вычислить определитель
A =  ,
,
в котором все элементы по одну сторону от главной диагонали равны
нулю.
Решение. Разложим определитель А по первой строке:
A = a11 A11 = 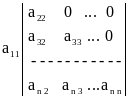 .
.
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
A = 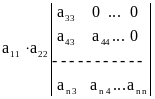 .
.
И так далее. После n шагов придем к равенству A = а11 а22... ann.
Пример 4. Вычислить определитель 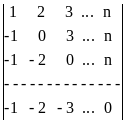 .
.
Решение. Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель:  , равный исходному.
, равный исходному.
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.







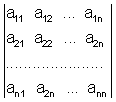 . (1)
. (1)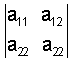 .
.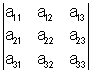 вычисляется по формуле
вычисляется по формуле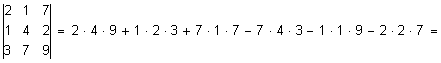
 . (4)
. (4) , показать, что он равен нулю.
, показать, что он равен нулю. , равный исходному. Если из третьей строки также вычесть первую, то получится определитель
, равный исходному. Если из третьей строки также вычесть первую, то получится определитель  , в котором две строки пропорциональны. Такой определитель равен нулю.
, в котором две строки пропорциональны. Такой определитель равен нулю.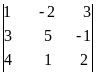 , разложив его по элементам второго столбца.
, разложив его по элементам второго столбца.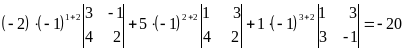 .
. ,
, .
. .
. .
. , равный исходному.
, равный исходному.









